22.3 矩形和菱形(第1课时)课件(共27张PPT)-八年级数学下册同步精品课堂(沪教版)
文档属性
| 名称 | 22.3 矩形和菱形(第1课时)课件(共27张PPT)-八年级数学下册同步精品课堂(沪教版) |

|
|
| 格式 | pptx | ||
| 文件大小 | 981.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-25 00:00:00 | ||
图片预览






文档简介
(共27张PPT)
2023-2024学年八年级下册数学同步精品课堂(沪教版)
第 22章 四边形
22.3矩形和菱形(第1课时)
学习目标
1、理解矩形、菱形的概念,知道它们与平行四边形之间的区别与联系。
2、掌握矩形、菱形的有关性质并能运用这些性质进行有关的证明和计算。
3、经历从平行四边形的性质类比探索矩形和菱形的性质的过程,感悟类比思想以及“从一般到特殊”的方法。
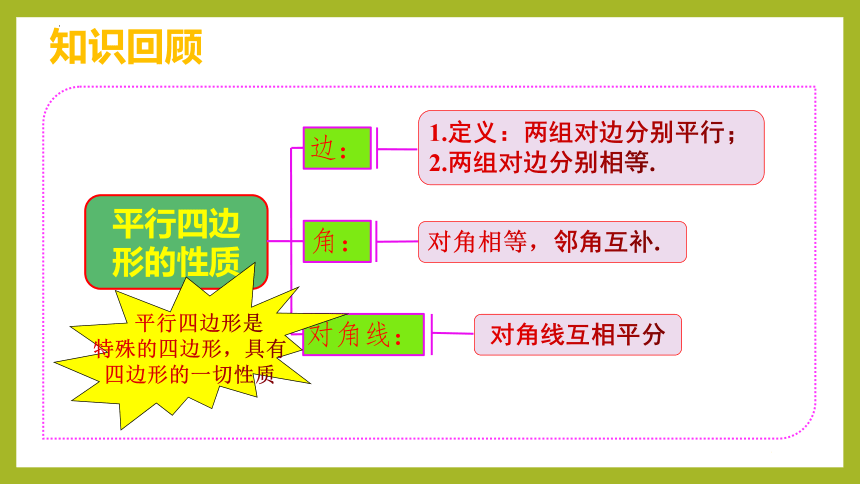
1.定义:两组对边分别平行;2.两组对边分别相等.平行四边形的性质边:对角线:角:对角相等,邻角互补.对角线互相平分平行四边形是特殊的四边形,具有四边形的一切性质知识回顾
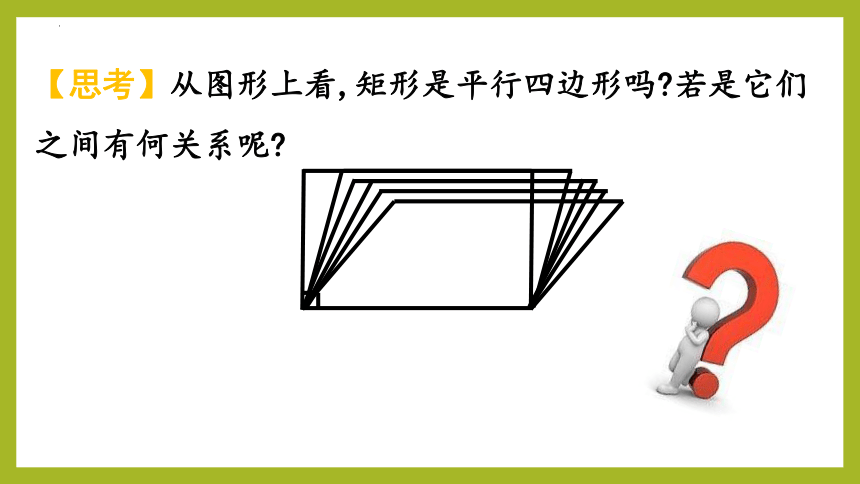
【思考】从图形上看,矩形是平行四边形吗 若是它们之间有何关系呢
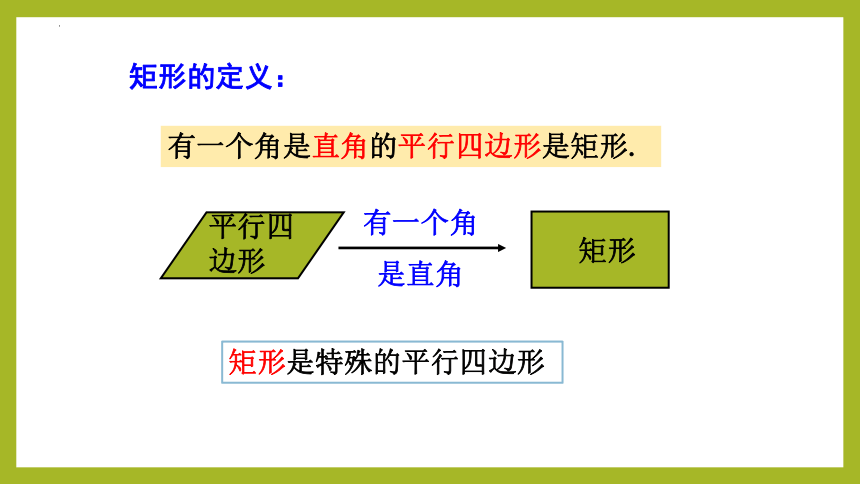
有一个角是直角的平行四边形是矩形.
矩形的定义:
平行四边形
矩形
有一个角
是直角
矩形是特殊的平行四边形
下面的图形中有你熟悉的吗?
越王勾践剑,一把在地下埋藏了2000多年的古剑,出土时依然寒气逼人,毫无锈蚀,锋利无比,稍一用力,便可将多层白纸划破,剑身上整齐排列的黑色菱形暗花纹.
菱形有哪些性质呢?
在平行四边形中,如果内角大小保持不变仅改变边的长度,能否得到一个特殊的平行四边形?``x``xk
平行四边形
有一组邻边相等的平行四边形
菱形
邻边相等
有一组 的
邻边相等
平行四边形叫做
A
D
C
B
∵四边形ABCD是平行四边形,
AB=BC,
∴四边形ABCD是菱形.
菱形.
菱形的定义:
几何语言:
有一个内角是直角
有一组邻边相等
矩形
菱形
平行四边形
矩形、菱形与平行四边形的关系
因为矩形和菱形是特殊的平行四边形,所以它们具有平行四边形的所有性质.另外,它们还有一些特殊的性质,我们仍然从它们的边、角和对角线来进行研究.
1.研究矩形、菱形的内角.
(1)由矩形的定义,可知它有一个内角是直角.如图 22 - 30矩形 ABCD 中,∠A 是直角.
因为矩形 ABCD 是平行四边形,所以∠A=∠C=90°,∠B=∠D; ∠ A+ ∠ B+ ∠ C+ ∠ D=360°.
可知∠ A= ∠ B= ∠ C= ∠ D=90°.
(2)由菱形的定义可知,它的内角没有特殊的性质
ABCD矩形的四个角都是直角.为什么 矩形的性质定理1∵四边形ABCD是矩形,∴∠A=∠B=∠C=∠D=90°.几何语言矩形的边具有什么性质?矩形角的性质2.研究矩形、菱形的边.
(1)由矩形的定义,可知它的边没有特殊的性质.
(2)由菱形的定义,可知它有一组邻边相等。如图 22 -31,菱形ABCD 中,AD=CD.
因为菱形 ABCD 是平行四边形,所以
AB=CD,BC=AD.
可知 AB=BC=AD=CD.
通过以上研究,得到菱形的一个特殊性质
菱形性质定理 1 菱形的四条边都相等
3.研究矩形、菱形的对角线.
(1)分析图 22-32 中矩形ABCD的对角线:
由 AB=DC,BC=CB,得 Rt△ABC≌Rt△DCB
可知 AC=BD.
(2)分析图 22-33 中菱形 ABCD 的对角线
设 AC与BD 相交于点O,可知
OA=OC,OB=OD( )
在△ACD 中,AD=CD,得DO⊥AC,∠ADO= ∠ CDO( ).
同理,可得∠ ABO= ∠ CBO, ∠ DAO= ∠ BAO, ∠ BCO= ∠ DCO.
两条对角线有何关系 矩形的两条对角线相等. 矩形的性质定理2如何证明 ∵四边形ABCD是矩形,∴AC=BD.几何语言矩形的对角线性质菱形性质定理 2 菱形的对角线互相垂直,并且每条对角线平分一组对角.
几何语言
∵四边形ABCD是菱形,
∴ AC⊥BD.
B
C
D
A
O
菱形的对角线性质
想一想
平行四边形是中心对称图形,矩形和菱形当然都是中心对称图形.进一步分析矩形和菱形,它们是轴对称图形吗
矩形和菱形都是轴对称图形,它们分别有两条对称轴.试画出它们的对称轴,再用语言叙述.
平行四边形、矩形、菱形的性质
矩形 菱形
边 共性 特性
角 共性 特性
对角线 共性 特性
对称性 共性 特性
对边平行且相等
对角相等,邻角互补
对角线互相平分
中心对称图形
四条边相等
四个角都是直角
对角线相等
对角线互相垂直,每一条对角线平分一组对角
轴对称图形
轴对称图形
1. 根据图形求出相应的 x、y 的值(第 1,3 个图是矩形,第 2 个图是菱形;第 3 个图中的 2x、2y+4、x+3y 分别表示矩形对角线一半的长):
课本练习
2、下列命题中,假命题是( )
A 矩形的对角线互相平分且相等
B 菱形的对角线互相平分且垂直
C 矩形的两条对角线把矩形分成四个直角三角形
D 菱形的两条对角线把菱形分成四个直角三角形
C
3.利用矩形的性质,证明:直角三角形斜边上的中线等于斜边的一半.
1.如图,在矩形ABCD中,对角线AC,BD交于点O,下列说法错误的是 ( )
A.AB∥DC B.AC=BD
C.AC⊥BD D.OA=OB
A
B
C
D
O
C
随堂检测
2.如图,在矩形ABCD中,E是BC上一点,AE=AD,DF⊥AE ,垂足为F.求证:DF=DC.
A
B
C
D
E
F
证明:连接DE.
∵AD =AE,∴∠AED =∠ADE.
∵四边形ABCD是矩形,∴AD∥BC,∠C=90°.
∴∠ADE=∠DEC, ∴∠DEC=∠AED.
又∵DF⊥AE, ∴∠DFE=∠C=90°.
又∵DE=DE,
.
∴△DFE≌△DCE.∴DF=DC.
3.如图,四边形ABCD是菱形,F是AB上一点,DF交AC于E.
求证:∠AFD=∠CBE.
证明:∵四边形ABCD是菱形,
∴CB=CD, CA平分∠BCD.
∴∠BCE=∠DCE.
又 CE=CE,∴△BCE≌△DCE(SAS).
∴∠CBE=∠CDE.
∵在菱形ABCD中,AB∥CD,
∴∠AFD=∠EDC.∴∠AFD=∠CBE.
A
D
C
B
F
E
矩形的相关概念及性质
具有平行四边形的一切性质
四个内角都是直角,
对角线相等
既是轴对称图形也是中心对称图形
直角三角形斜边上的中线等于斜边的一半
有一个角是直角的平行四边形叫做矩形
定义
性质
课堂小结
菱形的性质
边
角
对角线
1.两组对边平行且相等;
2.四条边相等
两组对角分别相等,邻角互补
1.两条对角线互相垂直平分;
2.每一条对角线平分一组对角
课堂小结
有一组邻边相等的平行四边形叫菱形
定义
2023-2024学年八年级下册数学同步精品课堂(沪教版)
第 22章 四边形
22.3矩形和菱形(第1课时)
学习目标
1、理解矩形、菱形的概念,知道它们与平行四边形之间的区别与联系。
2、掌握矩形、菱形的有关性质并能运用这些性质进行有关的证明和计算。
3、经历从平行四边形的性质类比探索矩形和菱形的性质的过程,感悟类比思想以及“从一般到特殊”的方法。
1.定义:两组对边分别平行;2.两组对边分别相等.平行四边形的性质边:对角线:角:对角相等,邻角互补.对角线互相平分平行四边形是特殊的四边形,具有四边形的一切性质知识回顾
【思考】从图形上看,矩形是平行四边形吗 若是它们之间有何关系呢
有一个角是直角的平行四边形是矩形.
矩形的定义:
平行四边形
矩形
有一个角
是直角
矩形是特殊的平行四边形
下面的图形中有你熟悉的吗?
越王勾践剑,一把在地下埋藏了2000多年的古剑,出土时依然寒气逼人,毫无锈蚀,锋利无比,稍一用力,便可将多层白纸划破,剑身上整齐排列的黑色菱形暗花纹.
菱形有哪些性质呢?
在平行四边形中,如果内角大小保持不变仅改变边的长度,能否得到一个特殊的平行四边形?``x``xk
平行四边形
有一组邻边相等的平行四边形
菱形
邻边相等
有一组 的
邻边相等
平行四边形叫做
A
D
C
B
∵四边形ABCD是平行四边形,
AB=BC,
∴四边形ABCD是菱形.
菱形.
菱形的定义:
几何语言:
有一个内角是直角
有一组邻边相等
矩形
菱形
平行四边形
矩形、菱形与平行四边形的关系
因为矩形和菱形是特殊的平行四边形,所以它们具有平行四边形的所有性质.另外,它们还有一些特殊的性质,我们仍然从它们的边、角和对角线来进行研究.
1.研究矩形、菱形的内角.
(1)由矩形的定义,可知它有一个内角是直角.如图 22 - 30矩形 ABCD 中,∠A 是直角.
因为矩形 ABCD 是平行四边形,所以∠A=∠C=90°,∠B=∠D; ∠ A+ ∠ B+ ∠ C+ ∠ D=360°.
可知∠ A= ∠ B= ∠ C= ∠ D=90°.
(2)由菱形的定义可知,它的内角没有特殊的性质
ABCD矩形的四个角都是直角.为什么 矩形的性质定理1∵四边形ABCD是矩形,∴∠A=∠B=∠C=∠D=90°.几何语言矩形的边具有什么性质?矩形角的性质2.研究矩形、菱形的边.
(1)由矩形的定义,可知它的边没有特殊的性质.
(2)由菱形的定义,可知它有一组邻边相等。如图 22 -31,菱形ABCD 中,AD=CD.
因为菱形 ABCD 是平行四边形,所以
AB=CD,BC=AD.
可知 AB=BC=AD=CD.
通过以上研究,得到菱形的一个特殊性质
菱形性质定理 1 菱形的四条边都相等
3.研究矩形、菱形的对角线.
(1)分析图 22-32 中矩形ABCD的对角线:
由 AB=DC,BC=CB,得 Rt△ABC≌Rt△DCB
可知 AC=BD.
(2)分析图 22-33 中菱形 ABCD 的对角线
设 AC与BD 相交于点O,可知
OA=OC,OB=OD( )
在△ACD 中,AD=CD,得DO⊥AC,∠ADO= ∠ CDO( ).
同理,可得∠ ABO= ∠ CBO, ∠ DAO= ∠ BAO, ∠ BCO= ∠ DCO.
两条对角线有何关系 矩形的两条对角线相等. 矩形的性质定理2如何证明 ∵四边形ABCD是矩形,∴AC=BD.几何语言矩形的对角线性质菱形性质定理 2 菱形的对角线互相垂直,并且每条对角线平分一组对角.
几何语言
∵四边形ABCD是菱形,
∴ AC⊥BD.
B
C
D
A
O
菱形的对角线性质
想一想
平行四边形是中心对称图形,矩形和菱形当然都是中心对称图形.进一步分析矩形和菱形,它们是轴对称图形吗
矩形和菱形都是轴对称图形,它们分别有两条对称轴.试画出它们的对称轴,再用语言叙述.
平行四边形、矩形、菱形的性质
矩形 菱形
边 共性 特性
角 共性 特性
对角线 共性 特性
对称性 共性 特性
对边平行且相等
对角相等,邻角互补
对角线互相平分
中心对称图形
四条边相等
四个角都是直角
对角线相等
对角线互相垂直,每一条对角线平分一组对角
轴对称图形
轴对称图形
1. 根据图形求出相应的 x、y 的值(第 1,3 个图是矩形,第 2 个图是菱形;第 3 个图中的 2x、2y+4、x+3y 分别表示矩形对角线一半的长):
课本练习
2、下列命题中,假命题是( )
A 矩形的对角线互相平分且相等
B 菱形的对角线互相平分且垂直
C 矩形的两条对角线把矩形分成四个直角三角形
D 菱形的两条对角线把菱形分成四个直角三角形
C
3.利用矩形的性质,证明:直角三角形斜边上的中线等于斜边的一半.
1.如图,在矩形ABCD中,对角线AC,BD交于点O,下列说法错误的是 ( )
A.AB∥DC B.AC=BD
C.AC⊥BD D.OA=OB
A
B
C
D
O
C
随堂检测
2.如图,在矩形ABCD中,E是BC上一点,AE=AD,DF⊥AE ,垂足为F.求证:DF=DC.
A
B
C
D
E
F
证明:连接DE.
∵AD =AE,∴∠AED =∠ADE.
∵四边形ABCD是矩形,∴AD∥BC,∠C=90°.
∴∠ADE=∠DEC, ∴∠DEC=∠AED.
又∵DF⊥AE, ∴∠DFE=∠C=90°.
又∵DE=DE,
.
∴△DFE≌△DCE.∴DF=DC.
3.如图,四边形ABCD是菱形,F是AB上一点,DF交AC于E.
求证:∠AFD=∠CBE.
证明:∵四边形ABCD是菱形,
∴CB=CD, CA平分∠BCD.
∴∠BCE=∠DCE.
又 CE=CE,∴△BCE≌△DCE(SAS).
∴∠CBE=∠CDE.
∵在菱形ABCD中,AB∥CD,
∴∠AFD=∠EDC.∴∠AFD=∠CBE.
A
D
C
B
F
E
矩形的相关概念及性质
具有平行四边形的一切性质
四个内角都是直角,
对角线相等
既是轴对称图形也是中心对称图形
直角三角形斜边上的中线等于斜边的一半
有一个角是直角的平行四边形叫做矩形
定义
性质
课堂小结
菱形的性质
边
角
对角线
1.两组对边平行且相等;
2.四条边相等
两组对角分别相等,邻角互补
1.两条对角线互相垂直平分;
2.每一条对角线平分一组对角
课堂小结
有一组邻边相等的平行四边形叫菱形
定义
