19.1.1.2函数(同步课件)-八年级数学下册同步精品课堂(人教版)
文档属性
| 名称 | 19.1.1.2函数(同步课件)-八年级数学下册同步精品课堂(人教版) |

|
|
| 格式 | pptx | ||
| 文件大小 | 50.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-25 09:30:41 | ||
图片预览







文档简介
(共28张PPT)
第19章
一次函数
八年级数学下册同步精品课堂(人教版)
人教版 数学
八年级 下册
19.1.1.2
函数
情景引入
国庆黄金周天气晴朗,小薇一家开着车去杭州小姨家作客,途中加油时的数字引起了小薇的兴趣,她将记录的数据整理成下表,请你帮忙完成.
油量(升) 金额(元)
0 0
2 16.64
4
66.56
12
266.24
情景引入
小薇在收音机里听到新中国成立以来,我国已经进行了七次人口普查,她将我国七次人口普查的人口数做成了统计表.
年份 人口数(亿)
1953 6.02
1964 7.23
1982 10.32
1990 11.60
2000 12.95
2010 13.71
2020 14.12
(1)在这一变化过程中,有几个变量?分别是什么?
(2)在这一变化过程中,两个变量之间有什么关系?
随着 的变化而变化.
人口数
年份
对于 的每一个值, 都有唯一的值与它对应.
年份
人口数
新知探究
姨父说最近村子里有黄鼠狼,小薇准备帮助姨父用一段20m长的栅栏围一个长方形鸡舍……
(1)当长方形的宽为2m时,长为 ____ m;
(2)当长方形的宽为4m时,长为 ____ m;
(3)当长方形的宽为b m时,长为 ______ m.
8
6
(10-b)
(4)长方形的长是宽的函数吗?为什么?
(5)长方形的宽是长的函数吗?为什么?
(6)长方形的面积是宽的函数吗?为什么?
新知探究
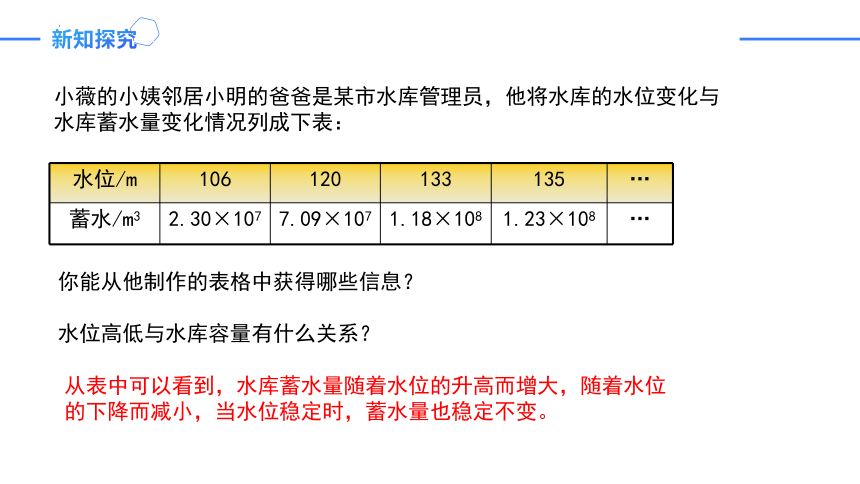
水位/m 106 120 133 135 …
蓄水/m3 2.30×107 7.09×107 1.18×108 1.23×108 …
你能从他制作的表格中获得哪些信息?
水位高低与水库容量有什么关系?
小薇的小姨邻居小明的爸爸是某市水库管理员,他将水库的水位变化与水库蓄水量变化情况列成下表:
从表中可以看到,水库蓄水量随着水位的升高而增大,随着水位的下降而减小,当水位稳定时,蓄水量也稳定不变。
情景引入
时间t(时)
8
10
2
4
6
12
14
16
18
20
22
24
0
温度T( C)
2
4
6
8
-2
-4
0
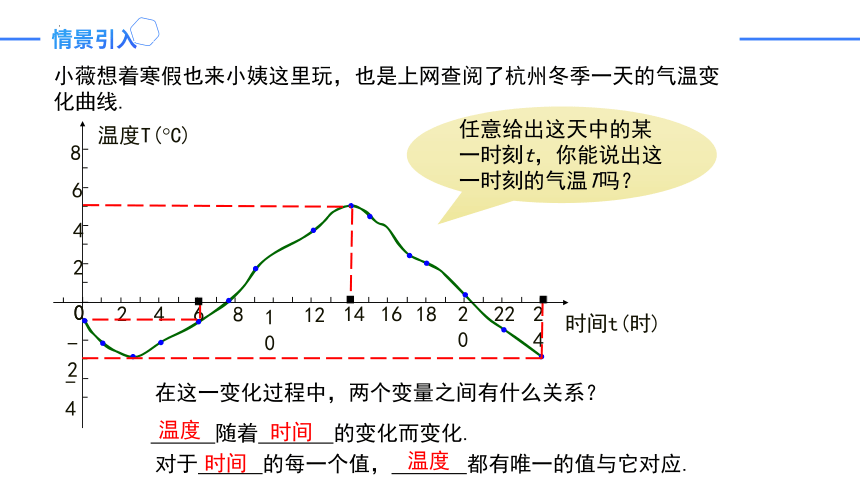
小薇想着寒假也来小姨这里玩,也是上网查阅了杭州冬季一天的气温变化曲线.
随着 的变化而变化.
任意给出这天中的某一时刻t,你能说出这一时刻的气温T吗?
对于 的每一个值, 都有唯一的值与它对应.
在这一变化过程中,两个变量之间有什么关系?
温度
时间
时间
温度
情景引入
同学们,你们能从刚才的几个变化过程中找到它们的共同之处吗?
对于 的每一个值,
有_____值与之对应.
金额与油量
两
唯一
随之变化
人口数与年份
温度与时间
每个变化过程中都有___个变量,
其中 变化时,
也___________;
x 和 y
一个变量
另一个变量
其中一个变量
另一个变量
鸡舍的长和宽
水位高低与水库容量
总结
新知探究
一般地,在某个变化过程中,如果有两个变量x与y,并且对于x的每一个确定的值,y都有唯一确定的值与它对应,那么我们就说x是自变量,y是x的函数.
如果当x=a时y=b,那么b叫做当自变量的值为a时的函数值.
新知探究
function
莱布尼兹
(德国)
李善兰
(清代)
凡此变数函彼变数,则此为彼之函数 .
(这里的“函”有包含的意思.)
函数
翻译
函数一语,起用于公元
1692 年,最早见自德国数
学家莱布尼兹的著作. 他
是德国最重要的自然科学
家、数学家、物理学家、
历史学家和哲学家,一个
举世罕见的科学天才,和
牛顿同为微积分的创建人。
他博览群书,涉猎百科,
对丰富人类的科学知识
宝库做出了不可磨灭的贡献。
典例精析
例1
下列表格反映了一个变化过程中y与x的关系,其中y 是x的函数吗?
(2)
(1)
典例精析
例2
(1)若每吨民用自来水的价格为2.8元,所交水费金额为y(元),使用自来水的数量为x(吨), 则 y 是 x 的函数吗?为什么?
(2)底边为6(m)的三角形面积为s(㎡),高为h (m), s是h的函数吗?为什么?
(3)根据小鱼的条数与所需火柴棒的根数的关系,s是n的函数吗?
为什么?
6n+2
s=6n+2
……
……
8
14
20
n
火柴的根数(s)
小鱼条数(n)
2
1
3
……
……
典例精析
例3
气温的摄氏度数x与华氏度数y之间可用数学式子
进行转化,华氏度数y是不是摄氏度数x的函数?为什么?
解:在把摄氏度转化为华氏度的过程中,华氏度y随着摄氏度x的变化而变化;
由 ,当x取一个值时,y的值也随之唯一确定,
例如下表:
摄氏度数x(℃) … -10 0 25 35 100 …
华氏度数y(℉) … …
14
32
77
95
212
所以y是x的函数.
典例精析
例4
下列变化过程中,两个变量之间是否存在确定的依赖关系?其中一个变量是另一个变量的函数吗?
近年来上海市区的环境绿化不断得到改善,下表是上海市区人均绿化面积变化的一些统计数据:
解:两个变量是年份和人均绿化面积。
由表可知,随着所列年份的变化,上海市区人均绿化面积也在变化;对于所列的每一个年份,在表格中都可以找到这一年人均绿化面积的数值. 所以人均绿化面积是年份的函数.
年份 2000 2001 2002 2003 2004 2005
人均绿化面积(㎡) 4.5 5.5 7.0 9.4 10.0 11.0
新知探究
请用含自变量的式子表示下列问题中的函数关系:
(1)汽车以60 km/h 的速度匀速行驶,行驶的时间为 t(单位:h),行驶的路程为 s(单位:km);
(2)多边形的边数为 n,内角和的度数为 y.
问题(1)中,t 取-2 有实际意义吗?
问题(2)中,n 取2 有意义吗?
例5
思考
新知探究
根据刚才问题的思考,你认为函数的自变量可以取任意值吗?
在实际问题中,函数的自变量取值范围往往是有限制的,在限制的范围内,函数才有实际意义;超出这个范围,函数没有实际意义,我们把这种自变量可以取的数值范围叫函数的自变量取值范围.
典例精析
例6
下列关于变量x ,y 的关系式:
y =5x-9;
y =-x2+32;
y =6|x|-1;
④ ;
⑤y2-6x=100,其中表示y 是x 的函数关系的是 .
判断一个变量是否是另一个变量的函数,关键是看当一个变量确定时,另一个变量是否有唯一确定的值与它对应.
一个x值有两个y 值与它对应
典例精析
例7
下列函数中自变量x的取值范围是什么?
.
0
.
-1
.
-2
-2
x取全体实数
典例精析
例8
解:根据等腰三角形的性质和三角形内角和定理,可知
2x+y=180°,
有 y=180°-2x.
由于等腰三角形的底角只能是锐角,所以自变量的取值范围是
0<x<90°.
y
x
等腰三角形顶角的度数y是底角度数x的函数,试写出这个函数关系式,并求出自变量x的取值范围.
典例精析
例9
汽车的油箱中有汽油50L,如果不再加油,那么油箱中的油量y(单位:L)随行驶里程x(单位:km)的增加而减少,平均耗油量为0.1L/km.
(1)写出表示y与x的函数关系的式子.
解:(1) 函数关系式为: y = 50-0.1x
(2)指出自变量x的取值范围;
(2) 由x≥0及50-0.1x ≥0
得 0 ≤ x ≤ 500
∴自变量的取值范围是 0 ≤ x ≤ 500
求函数自变量的取值范围
新知探究
① 函数表达式有意义
②要符合实际
4.表达式是复合式时,自变量的取值是使各式成立的公共解.
3.表达式是偶次根式时,自变量的取值必须使被开方数为非负数.表达式是奇次根式时,自变量取全体实数;
1.表达式是整式时,自变量取全体实数;
2.表达式是分式时,自变量的取值要使分母不为0;
典例精析
例10
已知函数
(1)求当x=2,3,-3时,函数的值;
(2)求当x取什么值时,函数的值为0.
解:(1)当x=2时,y= ;
当x=3时,y= ;
当x=-3时,y=7.
(2)令 解得x=
即当x= 时,y=0.
归纳总结
函数
概念:函数在某个变化过程中,如果有两个变量x与y,并且对于x的每一个确定的值,y都有唯一确定的值与它对应,那么x是自变量,y是x的函数.
函数值
自变量的取值范围
1.使函数解析式有意义
2.符合实际意义
当堂检测
1.设路程为s,时间为t,速度为v,当v=60时,路程和时间的关系式为 ,这个关系式中, 是常量,
是变量, 是 的函数.
60
s=60t
t和s
s
t
2.油箱中有油30kg,油从管道中匀速流出,1h流完,则油箱中剩余油量Q(kg)与流出时间t(min)之间的函数关系式是 ,自变量t的取值范围是 .
当堂检测
3.分别写出下列各问题中的函数关系及自变量的取值范围:
(1)某地民用电费标准为每度电 0.50 元,电费 y(元)是用电度数 x 的函数;
y = 0.5x (x ≥ 0)
(2)已知等腰三角形的面积为 20 cm2,设它的底边长为 x (cm),底边上的高 y (cm) 是 x的函数;
(x > 0)
(3)在一个半径为 10 cm 的圆形纸片中剪去一个半径为 r(cm)的同心圆,得到一个圆环,设圆环的面积为 S(cm2),S 是 r 的函数.
S = π(100 - r2)(0 < r < 10)
当堂检测
4.为了加强居民的节水意识,某市制定了如下用水收费标准:每户每月的用水不超过10吨时,水价为每吨1.2元;超过10吨时,超过部分按每吨1.8元收费,该市某户居民5月份用水x吨(x>10),应交水费y元.请求出y和x的表达式,并判断y是否为x的函数.
y =12+1.8(x-10)
=1.8x-6
解:
y是x的函数.
当堂检测
5.求下列函数中自变量 x 可以取值的范围:
(1)y=3x-2;
x 取任意实数;
x≥1;
(2)y=;
(3)y=;
(4)y= .
x≠-
x<
当堂检测
6.一个三角形的周长为y cm,三边长分别为 7cm,3cm和 xcm.
(1) 求y关于x的函数关系式;
y=x+10
(2) 求自变量x的取值范围.
4分析:三角形的三边关系应满足:两边之和大于第三边,两边之差小于第三边.即7-3y=x+10 (4y关于x的函数关系式:
第19章
一次函数
八年级数学下册同步精品课堂(人教版)
人教版 数学
八年级 下册
19.1.1.2
函数
情景引入
国庆黄金周天气晴朗,小薇一家开着车去杭州小姨家作客,途中加油时的数字引起了小薇的兴趣,她将记录的数据整理成下表,请你帮忙完成.
油量(升) 金额(元)
0 0
2 16.64
4
66.56
12
266.24
情景引入
小薇在收音机里听到新中国成立以来,我国已经进行了七次人口普查,她将我国七次人口普查的人口数做成了统计表.
年份 人口数(亿)
1953 6.02
1964 7.23
1982 10.32
1990 11.60
2000 12.95
2010 13.71
2020 14.12
(1)在这一变化过程中,有几个变量?分别是什么?
(2)在这一变化过程中,两个变量之间有什么关系?
随着 的变化而变化.
人口数
年份
对于 的每一个值, 都有唯一的值与它对应.
年份
人口数
新知探究
姨父说最近村子里有黄鼠狼,小薇准备帮助姨父用一段20m长的栅栏围一个长方形鸡舍……
(1)当长方形的宽为2m时,长为 ____ m;
(2)当长方形的宽为4m时,长为 ____ m;
(3)当长方形的宽为b m时,长为 ______ m.
8
6
(10-b)
(4)长方形的长是宽的函数吗?为什么?
(5)长方形的宽是长的函数吗?为什么?
(6)长方形的面积是宽的函数吗?为什么?
新知探究
水位/m 106 120 133 135 …
蓄水/m3 2.30×107 7.09×107 1.18×108 1.23×108 …
你能从他制作的表格中获得哪些信息?
水位高低与水库容量有什么关系?
小薇的小姨邻居小明的爸爸是某市水库管理员,他将水库的水位变化与水库蓄水量变化情况列成下表:
从表中可以看到,水库蓄水量随着水位的升高而增大,随着水位的下降而减小,当水位稳定时,蓄水量也稳定不变。
情景引入
时间t(时)
8
10
2
4
6
12
14
16
18
20
22
24
0
温度T( C)
2
4
6
8
-2
-4
0
小薇想着寒假也来小姨这里玩,也是上网查阅了杭州冬季一天的气温变化曲线.
随着 的变化而变化.
任意给出这天中的某一时刻t,你能说出这一时刻的气温T吗?
对于 的每一个值, 都有唯一的值与它对应.
在这一变化过程中,两个变量之间有什么关系?
温度
时间
时间
温度
情景引入
同学们,你们能从刚才的几个变化过程中找到它们的共同之处吗?
对于 的每一个值,
有_____值与之对应.
金额与油量
两
唯一
随之变化
人口数与年份
温度与时间
每个变化过程中都有___个变量,
其中 变化时,
也___________;
x 和 y
一个变量
另一个变量
其中一个变量
另一个变量
鸡舍的长和宽
水位高低与水库容量
总结
新知探究
一般地,在某个变化过程中,如果有两个变量x与y,并且对于x的每一个确定的值,y都有唯一确定的值与它对应,那么我们就说x是自变量,y是x的函数.
如果当x=a时y=b,那么b叫做当自变量的值为a时的函数值.
新知探究
function
莱布尼兹
(德国)
李善兰
(清代)
凡此变数函彼变数,则此为彼之函数 .
(这里的“函”有包含的意思.)
函数
翻译
函数一语,起用于公元
1692 年,最早见自德国数
学家莱布尼兹的著作. 他
是德国最重要的自然科学
家、数学家、物理学家、
历史学家和哲学家,一个
举世罕见的科学天才,和
牛顿同为微积分的创建人。
他博览群书,涉猎百科,
对丰富人类的科学知识
宝库做出了不可磨灭的贡献。
典例精析
例1
下列表格反映了一个变化过程中y与x的关系,其中y 是x的函数吗?
(2)
(1)
典例精析
例2
(1)若每吨民用自来水的价格为2.8元,所交水费金额为y(元),使用自来水的数量为x(吨), 则 y 是 x 的函数吗?为什么?
(2)底边为6(m)的三角形面积为s(㎡),高为h (m), s是h的函数吗?为什么?
(3)根据小鱼的条数与所需火柴棒的根数的关系,s是n的函数吗?
为什么?
6n+2
s=6n+2
……
……
8
14
20
n
火柴的根数(s)
小鱼条数(n)
2
1
3
……
……
典例精析
例3
气温的摄氏度数x与华氏度数y之间可用数学式子
进行转化,华氏度数y是不是摄氏度数x的函数?为什么?
解:在把摄氏度转化为华氏度的过程中,华氏度y随着摄氏度x的变化而变化;
由 ,当x取一个值时,y的值也随之唯一确定,
例如下表:
摄氏度数x(℃) … -10 0 25 35 100 …
华氏度数y(℉) … …
14
32
77
95
212
所以y是x的函数.
典例精析
例4
下列变化过程中,两个变量之间是否存在确定的依赖关系?其中一个变量是另一个变量的函数吗?
近年来上海市区的环境绿化不断得到改善,下表是上海市区人均绿化面积变化的一些统计数据:
解:两个变量是年份和人均绿化面积。
由表可知,随着所列年份的变化,上海市区人均绿化面积也在变化;对于所列的每一个年份,在表格中都可以找到这一年人均绿化面积的数值. 所以人均绿化面积是年份的函数.
年份 2000 2001 2002 2003 2004 2005
人均绿化面积(㎡) 4.5 5.5 7.0 9.4 10.0 11.0
新知探究
请用含自变量的式子表示下列问题中的函数关系:
(1)汽车以60 km/h 的速度匀速行驶,行驶的时间为 t(单位:h),行驶的路程为 s(单位:km);
(2)多边形的边数为 n,内角和的度数为 y.
问题(1)中,t 取-2 有实际意义吗?
问题(2)中,n 取2 有意义吗?
例5
思考
新知探究
根据刚才问题的思考,你认为函数的自变量可以取任意值吗?
在实际问题中,函数的自变量取值范围往往是有限制的,在限制的范围内,函数才有实际意义;超出这个范围,函数没有实际意义,我们把这种自变量可以取的数值范围叫函数的自变量取值范围.
典例精析
例6
下列关于变量x ,y 的关系式:
y =5x-9;
y =-x2+32;
y =6|x|-1;
④ ;
⑤y2-6x=100,其中表示y 是x 的函数关系的是 .
判断一个变量是否是另一个变量的函数,关键是看当一个变量确定时,另一个变量是否有唯一确定的值与它对应.
一个x值有两个y 值与它对应
典例精析
例7
下列函数中自变量x的取值范围是什么?
.
0
.
-1
.
-2
-2
x取全体实数
典例精析
例8
解:根据等腰三角形的性质和三角形内角和定理,可知
2x+y=180°,
有 y=180°-2x.
由于等腰三角形的底角只能是锐角,所以自变量的取值范围是
0<x<90°.
y
x
等腰三角形顶角的度数y是底角度数x的函数,试写出这个函数关系式,并求出自变量x的取值范围.
典例精析
例9
汽车的油箱中有汽油50L,如果不再加油,那么油箱中的油量y(单位:L)随行驶里程x(单位:km)的增加而减少,平均耗油量为0.1L/km.
(1)写出表示y与x的函数关系的式子.
解:(1) 函数关系式为: y = 50-0.1x
(2)指出自变量x的取值范围;
(2) 由x≥0及50-0.1x ≥0
得 0 ≤ x ≤ 500
∴自变量的取值范围是 0 ≤ x ≤ 500
求函数自变量的取值范围
新知探究
① 函数表达式有意义
②要符合实际
4.表达式是复合式时,自变量的取值是使各式成立的公共解.
3.表达式是偶次根式时,自变量的取值必须使被开方数为非负数.表达式是奇次根式时,自变量取全体实数;
1.表达式是整式时,自变量取全体实数;
2.表达式是分式时,自变量的取值要使分母不为0;
典例精析
例10
已知函数
(1)求当x=2,3,-3时,函数的值;
(2)求当x取什么值时,函数的值为0.
解:(1)当x=2时,y= ;
当x=3时,y= ;
当x=-3时,y=7.
(2)令 解得x=
即当x= 时,y=0.
归纳总结
函数
概念:函数在某个变化过程中,如果有两个变量x与y,并且对于x的每一个确定的值,y都有唯一确定的值与它对应,那么x是自变量,y是x的函数.
函数值
自变量的取值范围
1.使函数解析式有意义
2.符合实际意义
当堂检测
1.设路程为s,时间为t,速度为v,当v=60时,路程和时间的关系式为 ,这个关系式中, 是常量,
是变量, 是 的函数.
60
s=60t
t和s
s
t
2.油箱中有油30kg,油从管道中匀速流出,1h流完,则油箱中剩余油量Q(kg)与流出时间t(min)之间的函数关系式是 ,自变量t的取值范围是 .
当堂检测
3.分别写出下列各问题中的函数关系及自变量的取值范围:
(1)某地民用电费标准为每度电 0.50 元,电费 y(元)是用电度数 x 的函数;
y = 0.5x (x ≥ 0)
(2)已知等腰三角形的面积为 20 cm2,设它的底边长为 x (cm),底边上的高 y (cm) 是 x的函数;
(x > 0)
(3)在一个半径为 10 cm 的圆形纸片中剪去一个半径为 r(cm)的同心圆,得到一个圆环,设圆环的面积为 S(cm2),S 是 r 的函数.
S = π(100 - r2)(0 < r < 10)
当堂检测
4.为了加强居民的节水意识,某市制定了如下用水收费标准:每户每月的用水不超过10吨时,水价为每吨1.2元;超过10吨时,超过部分按每吨1.8元收费,该市某户居民5月份用水x吨(x>10),应交水费y元.请求出y和x的表达式,并判断y是否为x的函数.
y =12+1.8(x-10)
=1.8x-6
解:
y是x的函数.
当堂检测
5.求下列函数中自变量 x 可以取值的范围:
(1)y=3x-2;
x 取任意实数;
x≥1;
(2)y=;
(3)y=;
(4)y= .
x≠-
x<
当堂检测
6.一个三角形的周长为y cm,三边长分别为 7cm,3cm和 xcm.
(1) 求y关于x的函数关系式;
y=x+10
(2) 求自变量x的取值范围.
4
