第2章四边形复习课 课件(共64张PPT)-湘教版数学八年级下册
文档属性
| 名称 | 第2章四边形复习课 课件(共64张PPT)-湘教版数学八年级下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-25 00:00:00 | ||
图片预览







文档简介
(共64张PPT)
湘教版·初中数学·八年级下册·第2章
第2章 四边形
复习课
复习目标
1.理解平行四边形、矩形、菱形、正方形概念之间的 联系和区别.
2.能用正方形的定义、性质和判定进行推理与计算.
3.掌握多边形内角和与外角和中心对称的性质与三角形中位线的性质并能应用。
学习重点:
根据具体问题情境,选择适当的知识进行推理计算.
。
1. n边形的内角和等于 。n边形的外角和等于 。
(n-2) ·180°
360°
②、中点 + = 中位线
2、三角形的中位线定理:
三角形的中位线平行于第三边,并且等于第三边的一半。
简单记忆
①、中点 + = 中位线
中点
平行
3、中心对称图形的特征
在成中心对称的两个图形中,对应点所连线段都经过 ,并且被对称中心________.
对称中心
平分
复习引入
一、多边形的内角和与外角和
多边形的内角和等于
多边形的外角和等于
正多边形每个内角的度数是
正多边形每个外角的度数是
要点梳理
(n-2) ×180 °
360 °
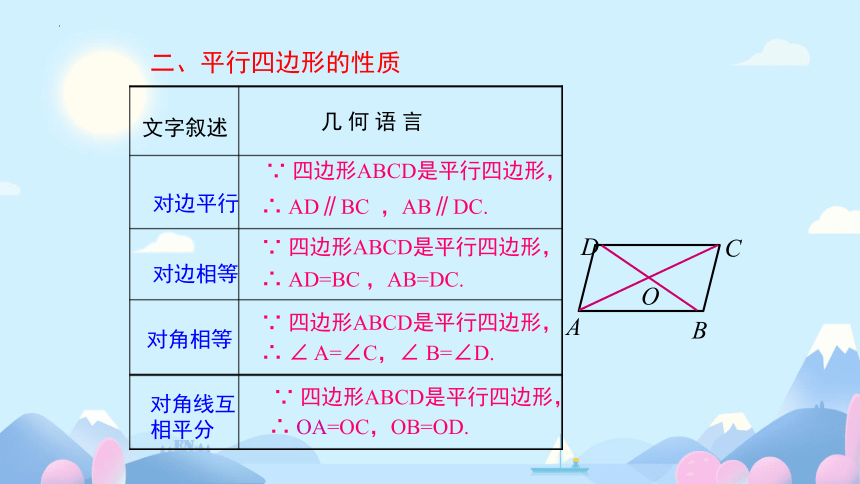
几 何 语 言
文字叙述
对边平行
对边相等
对角相等
∴ AD=BC ,AB=DC.
∵ 四边形ABCD是平行四边形,
∴ ∠ A=∠C,∠ B=∠D.
∵ 四边形ABCD是平行四边形,
二、平行四边形的性质
对角线互
相平分
∵ 四边形ABCD是平行四边形,
∴ OA=OC,OB=OD.
∵ 四边形ABCD是平行四边形,
∴ AD∥BC ,AB∥DC.
A
B
C
D
O
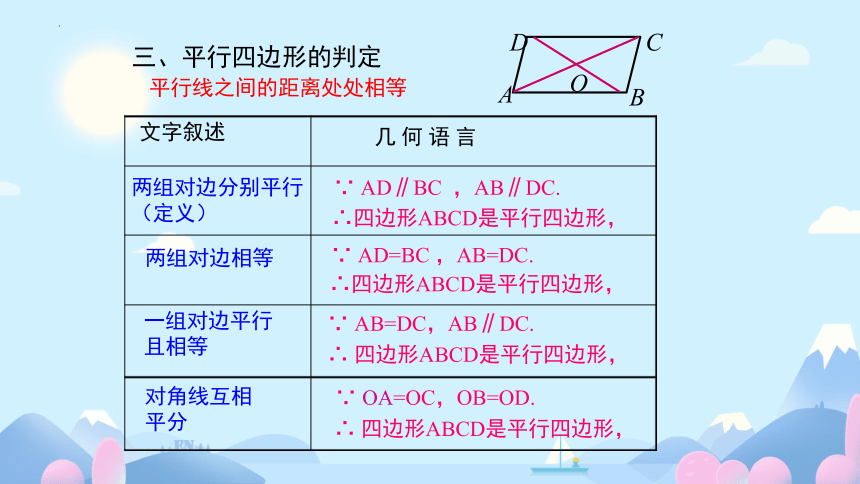
几 何 语 言
文字叙述
两组对边相等
一组对边平行且相等
∴四边形ABCD是平行四边形,
∵ AD=BC ,AB=DC.
∴ 四边形ABCD是平行四边形,
∵ AB=DC,AB∥DC.
三、平行四边形的判定
对角线互相平分
∴ 四边形ABCD是平行四边形,
∵ OA=OC,OB=OD.
两组对边分别平行(定义)
∴四边形ABCD是平行四边形,
∵ AD∥BC ,AB∥DC.
平行线之间的距离处处相等
A
B
C
D
O
1.中心对称
把一个图形绕着某一个点旋转____,如果它能与另一个图形重合,那么就说这两个图形成中心对称,这个点叫做对称中心,这两个图形中的对应点叫做关于中心的对称点.
180°
四、中心对称
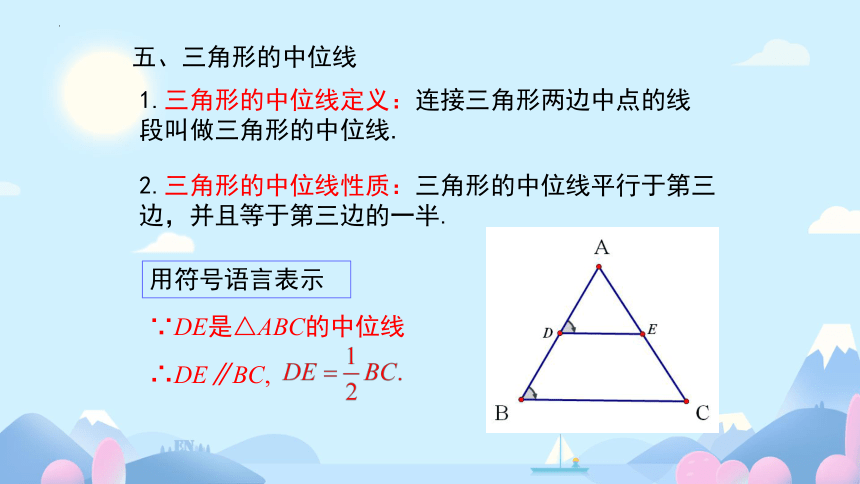
1.三角形的中位线定义:连接三角形两边中点的线段叫做三角形的中位线.
2.三角形的中位线性质:三角形的中位线平行于第三边,并且等于第三边的一半.
五、三角形的中位线
用符号语言表示
∵DE是△ABC的中位线
∴DE∥BC,
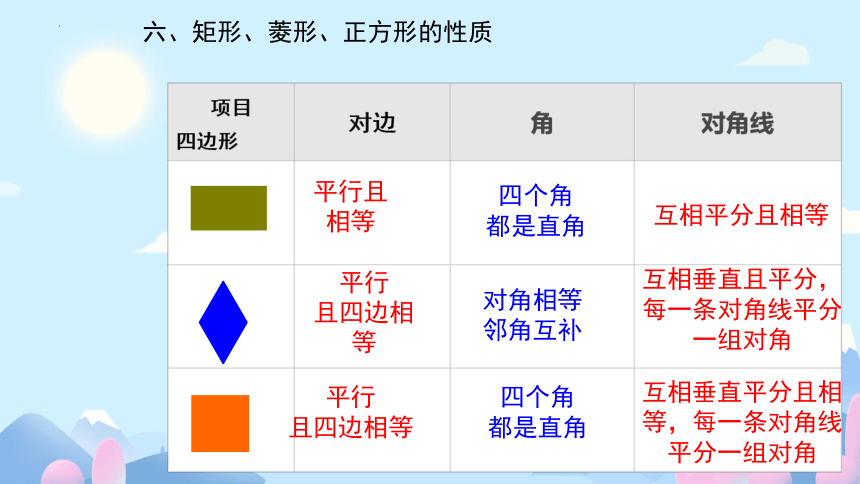
平行且相等
平行
且四边相等
平行
且四边相等
四个角
都是直角
对角相等
邻角互补
四个角
都是直角
互相平分且相等
互相垂直平分且相等,每一条对角线平分一组对角
互相垂直且平分,每一条对角线平分一组对角
六、矩形、菱形、正方形的性质
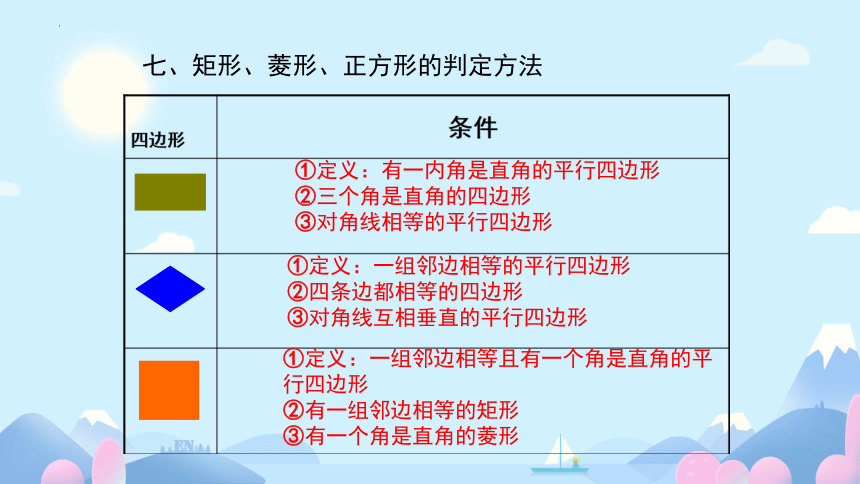
①定义:有一内角是直角的平行四边形
②三个角是直角的四边形
③对角线相等的平行四边形
①定义:一组邻边相等的平行四边形
②四条边都相等的四边形
③对角线互相垂直的平行四边形
①定义:一组邻边相等且有一个角是直角的平行四边形
②有一组邻边相等的矩形
③有一个角是直角的菱形
七、矩形、菱形、正方形的判定方法
知识点1 多边形的内角和、外角和
1. n边形的内角和等于________________.
2. 任意多边形的外角和等于 _______.
3. 在平面内,_______________________的多边形叫作正多边形.
4. 三角形具有稳定性,四边形具有_____________.
(n-2)·180°
360°
边相等、角也相等
不稳定性
例1 一个正多边形的内角和为1080°,则这个正多边形的每一个外角等于( )
A. 30° B. 45°
C. 60° D. 72°
B
解析 设多边形的边数为n,则
(n-2)×180°=1080°,解得n=8.
它的每一个外角为360°÷8=45°,
故选B.
做一做 (莱芜中考)一个多边形的内角和比其外角和的2倍多180°,则该多边形的对角线的条数是( )
A. 12 B. 13
C. 14 D. 15
解析 设多边形的边数为n,则(n-2)×180°=360°×2+180°,解得n=7.该多边形的对角线的条数为7×(7 3)/2=14,故选C
C
注意 从n边形的一个顶点出发,有(n-3)条对角线把n边形分成(n-3)个三角形,其内角和公式由三角形的内角和得到.
重要提示
1. n边形有n个内角,每一个顶点处的一个外角与内角的和等于180°;
2. 正多边形的各个内角相等,各个外角相等;
3. 一般地,求多边形的内角和,直接利用外角和公式计算;求多边形的边数,利用n边形的外角和公式和外角和等于360°列出方程求解.
知识点2 平行四边形的性质
1. 平行四边形的对边_________________.
2. 平行四边形的对角_________,邻角__________.
3. 平行四边形的对角线____________________.
4. 平行四边形是__________对称图形,但不是_________对称图形.
平行且相等
相等
互补
互相平分
中心
轴
例2 如图,在□ABCD中,对角线AC,BD相交于点O,过点O任意作直线EF分别交AD,BC于点E,F.
(1) 求证:OE=OF.
(2) 若AB=EF=8,BC=10,求四边形EFCD的周长.
(1)证明 ∵ 四边形ABCD是平行四边形,∴ OA=OC,AD∥BC.
∴ ∠AEO=∠CFO,∠EAO=∠FCO.
∴ △AEO≌△AEO.
∴ OE=OF.
(2)解 ∵ △AEO≌△AEO,
∴ AE=CF.
又∵ AD=BC,即AE+DE=BF+CF.
∴ DE=BF.
∴ DE+CF=BF+CF=BC=10.
∵ AB=CD,AB=8.
∴ CD=8.
∴ 四边形EFCD的周长为DE+CF+EF+CD=10+8+8=26.
做一做 (侯马市期末)如图,在□ABCD中,AC,BD交于点O,AE⊥BD于点E,BD=20,BE=7,AE=4,则AC的长等于____________.
在Rt△AOE中,由勾股定理得
OA= ,从而
AC=2OA=10.
解析 ∵ 四边形ABCD是平行四边形,
BD=20,BE=7,
∴ OB= BD=10,OE=OB-BE=3.
10
重要提示
已知平行四边形解决角和线段的问题,要注意:
1. 根据平行四边形的性质,得出所需要的结论;
2. 用得到的结论作为条件,判定两个三角形全等,或判定一个三角形是等腰三角形或直角三角形等;
3. 利用三角形、全等三角形的性质解决问题;
4. 一条对角线把平行四边形分成两个全等的三角形,两条对角线把平行四边形分成两对全等的三角形.
知识点3 平行四边形的判定
1. 两组对边_____________的四边形叫作平行四边形.
2. 一组对边 _____________ 的四边形是平行四边形.
3. 两组对边_____________的四边形是平行四边形.
4. 两组对角_____________的四边形是平行四边形.
5. 对角线_______________的四边形是平行四边形.
分别平行
平行且相等
分别相等
分别相等
互相平分
例3 如图,在□ABCD中,E,F是对角线BD上的点,且DE=BF.
求证:四边形AECF是平行四边形.
思路1 运用判定定理“一组对边平行且相等的四边形是平行四边形”,先证AE∥CF,且AE∥CF.
思路2 运用判定定理“对角线互相平分的四边形是平行四边形”,连接AC,交BD与点O,则OA=OC,证OE=OF即可.
证法一 ∵ 四边形ABCD是平行四边形,
∴ AD=BC,AD∥BC.
∴ ∠ADE=∠CBF.
又∵ DE=BF,
∴ △ADE≌△CBF.
∴ AE=CF,∠AED=∠CFB.
∴ AE∥CF.
∴ 四边形AECF是平行四边形.
证法二 连接BD.
∵ 四边形ABCD是平行四边形,
∴ OA=OC,OB=OD.
又∵ BF=DE,
∴ BF-OB=DE-OD.
∴ OF=OE.
∴ 四边形AECF是平行四边形.
做一做 如图,在四边形ABCD中,BE平分∠ABC交DA于点E,AB=AE,添加下列条件,一定能判定四边形ABCD是平行四边形的是( )
A. AB=CD
B. AD=BC
C. BE=BC
D. ∠A=∠D
B
重要提示
平行四边形的判定,要注意:
1. 根据条件和问题,正确选择判定方法;
2. 要充分利用已知平行四边形或三角形的性质得到判定平行四边形的条件,必要时需添加辅助线如对角线等;
3. 注意推理严密,语言规范.
知识点4 中心对称与中心对称图形
1. 在平面内,如果一个图形G绕点O旋转 ________,得到的像与另一个图形G′重合,那么称这两个图形关于点O中心对称,点O叫作_____________.
2. 成中心对称的两个图形中,对应点的连线经过对称中心,并且被对称中心________.
3. 如果一个图形绕一个点O旋转180°,所得到的像与原来的图形重合,那么这个图形叫作_______________,这个点O叫作它的对称中心.
对称中心
180°
平分
中心对称图形
例4 如图,已知△ACE和△DBF是关于某一点成中心对称的两个图形,连接BE,CF.
(1) 作出对称中心.
(2) 求证:四边形BECF是平行四边形.
(1)解 连接EF,交BC于点O,则点O为△ACE和△DBF的对称中心.
(2)证明 ∵ 点B和点C,点E和点F分别是两个成中心对称三角形的对称点,
∴ OB=OC,OE=OF.
∴ 四边形BECF是平行四边形.
做一做 1. 下列图形中,是中心对称图形但不是轴对称图形的是( )
A. 平行四边形
B. 矩形
C. 菱形
D. 正六边形
A
2. 下列图形中,是轴对称图形但不是中心对称图形的是( )
C
重要提示
解决中心对称与中心对称图形问题,要注意:
1. 明确对称中心——两组对应点连线的交点;
2. 根据对应中心和对应点得出相等的线段(边)和角.
知识点5 三角形的中位线
1. 连接三角形两边 _______的线段叫作三角形的中位线.
2. 三角形的中位线__________第三边,并且等于_______________.
3. 过三角形一边的中点,并且平行于另一边的直线,一定
经过第三边的______.
中点
平行于
第三边的一半
中点
例5 如图,在△ABC中,点E,F,G分别是边AB,BC,CA的中点,AD⊥BC,AB=10,BD=8,CD=4.
(1)求证:∠EDG=∠EFG.
(2)求四边形ABCD的周长和
四边形AEDG的面积.
(1)证明 ∵ EF,FG是△ABC的中线,AD⊥BC,AB=6,
∴ EF∥AG,FG∥AE.
∴ 四边形ABCD是平行四边形.
∴∠EFG=∠EAG.
又∵ AD⊥BC,
∴ ∠ADB=∠ADC=90°.
∴ DE= AB=AE,DG= AC=AG.
∴ ∠DAE=∠ADE,∠DAG=∠ADG.
∴ ∠DAE+∠DAG=∠ADE+∠ADG,即∠EAG=∠EDG.
∴ ∠EFG==∠EDG.
(2)解 在Rt△ABD中,∠ADB=90°,AB=10,BD=8,根据勾股定理,得
AD=
在Rt△ACD中,∠ADC=90°,AD=6,CD=4,根据勾股定理,得 AC= .
∵ EF,FG是△ABC的中位线,四边形ABCD是平行四边形
∴ EF=AG= AC,FG=AE= AB.
∴ EF+AG+FG+AE=AB+AC=10+ .
即四边形ABCD的周长为10+ .
如图,连接EG,交AD为点O,则 EF是△ABC的中位线,
∴ EG= BC= (BD+DC)= (8+4)=6,EG∥BC.
又∵ AD⊥BC,
∴ AD⊥EG.
∴
= EG(AO+DO)= EG·AD= ×6× = .
做一做 如图,□ABCD的对角线AC,BD相交于点O,OE∥AB,下列判断中正确的是( )
A. AD=2OE
B. AC=2OE
C. BD=2OE
D. CD=2OE
D
重要提示
解决与三角形的中位线有关的问题,应注意:
1. 从数量和位置两个方面准确运用三角形的中位线性质;
2. 问题中如果有条件:已知三角形的中点,则可以尝试添加辅助线——三角形的中线或中位线解决问题.
考点一 多边形的内角和与外角和
例1:已知一个多边形的每个外角都是其相邻内角度数的 ,求这个多边形的边数.
解: 设此多边形的外角的度数为x,则内角的度数为4x,
则x+4x=180°,解得 x=36°.
∴边数n=360°÷36°=10.
考点讲练
1.一个正多边形的每一个内角都等于120 °,则其边数是 .
6
【解析】 因为该多边形的每一个内角都等于120°,所以它的每一个外角都等于60 °.所以边数是6.
归纳拓展
在多边形的有关求边数或内角、外角度数的问题中,要注意内角与外角之间的转化,以及定理的运用.尤其在求边数的问题中,常常利用定理列出方程,进而再求得边数.
针对训练
考点二 平行四边形的性质
例2 如图,在平行四边形ABCD中,下列结论中错误的是( )
A.∠1=∠2 B.∠BAD=∠BCD
C.AB=CD D.AC=BC
【解析】A.∵四边形ABCD是平行四边形,
∴AB∥CD,∴∠1=∠2,故A正确;
B.∵四边形ABCD是平行四边形,
∴∠BAD=∠BCD,故B正确;
C.∵四边形ABCD是平行四边形,
∴AB=CD,故C正确;
D
方法总结
主要考查了平行四边形的性质,关键是掌握平行四边形对边相等且平行,对角相等.
针对训练
2.如图,已知 ABCD中,AE平分∠BAD,CF平分∠BCD,分别交BC、AD于E、F.求证:AF=EC.
证明:∵四边形ABCD是平行四边形,
∴∠B=∠D,AD=BC,AB=CD,∠BAD=∠BCD,
(平行四边形的对角相等,对边相等)
∵AE平分∠BAD,CF平分∠BCD,
∴∠EAB= ∠BAD,∠FCD= ∠BCD,∴∠EAB= ∠FCD,
在△ABE和△CDF中
∠B=∠D
AB=CD ∴△ABE≌△CDF,∴BE=DF.
∠EAB=∠FCD
∵AD=BC ∴AF=EC.
例3 如图,在 ABCD中,∠ODA=90°,AC=10cm,BD=6cm,则AD的长为( )
A.4cm B.5cm C.6cm D.8cm
【解析】∵四边形ABCD是平行四边形,
AC=10cm,BD=6cm
∴OA=OC= AC=5cm,OB=OD= BD=3cm,
∵∠ODA=90°,
∴AD= =4cm.
A
方法总结
主要考查了平行四边形的性质,平行四边形的对角线互相平分,解题时还要注意勾股定理的应用.
【解析】∵在 ABCD中,对角线AC和BD交于点O,AC=24cm,BD=38cm,AD=28cm,
∴AO=CO=12cm,BO=19cm,AD=BC=28cm,
∴△BOC的周长是:BO+CO+BC=12+19+28=59(cm).
针对训练
3.如图,在 ABCD中,对角线AC和BD交于点O,AC=24cm,BD=38cm,AD=28cm,则△BOC的周长是( )
A.45cm B.59cm C.62cm D.90cm
B
考点三 平行四边形的判定
例4 如图,四边形ABCD的对角线交于点O,下列哪组条件不能判断四边形ABCD是平行四边形( )
A.OA=OC,OB=OD
B.∠BAD=∠BCD,AB∥CD
C.AD∥BC,AD=BC
D.AB=CD,AO=CO
D
平行四边形的判定方法:
①两组对边分别平行的四边形是平行四边形;
②两组对边分别相等的四边形是平行四边形;
③两组对角分别相等的四边形是平行四边形;
④对角线互相平分的四边形是平行四边形;
⑤一组对边平行且相等的四边形是平行四边形.
方法总结
考点四 中心对称及中心对称图形
例5 下列图形中,既是轴对称图形,又是中心对称图形的是( ).
A B C D
D
【解析】 图A.图B都是轴对称图形,图C是中心对称图形,图D既是中心对称图形也是轴对称图形.
考点五 三角形的中位线
例6 已知:AD是△ABC的中线,E是AD的中点,F是BE的延长线与AC的交点.求证: .
证明:过点D作DH∥BF,交AC于点H.
∵AD是△ABC的中线.
∴D是BC的中点.
∴CH=HF= CF
∵E是AD的中点,EF∥DH.
∴AF=FH.
∴AF= FC
A
B
C
D
E
F
H
例7:如图,在矩形ABCD中,两条对角线相交于点O,
∠AOD=120°,AB=2.5 ,求矩形对角线的长.
解:∵四边形ABCD是矩形.
∴AC = BD(矩形的对角线相等).
OA= OC= AC,OB = OD = BD ,
(矩形对角线相互平分)
∴OA = OD.
A
B
C
D
O
考点六 矩形的性质和判定
A
B
C
D
O
∵∠AOD=120°,
∴∠ODA=∠OAD= (180°- 120°)=30°.
又∵∠DAB=90° ,
(矩形的四个角都是直角)
∴BD = 2AB = 2 ×2.5 = 5.
例8:如图,在菱形ABCD中,对角线AC与BD相交于点O,∠BAD=60°,BD =6,求菱形的边长AB和对角线AC的长.
解:∵四边形ABCD是菱形,
∴AC⊥BD(菱形的对角线互相垂直)
OB=OD= BD = ×6=3(菱形的对角线互相平分)
在等腰三角形ABC中,
∵∠BAD=60°,
∴△ABD是等边三角形.
∴AB = BD = 6.
∴在Rt△AOB中,AO
∴AC=2AO=
A
B
C
O
D
考点七 菱形的性质和判定
巩固练习
1. 一个正多边形的内角和是1260°,则它的每一个外角的度数等于( )
A. 30°
B. 40°
C. 60°
D. 72°
B
2. 如图,在□ABCD中,对角线AC,BD相交于点O,下列说法中不正确的是( )
A. AB=CD
B. OB=OD
C. ∠ABD=∠DCA
D. ∠BAD+∠ADC=180°
C
3. 如图,下列条件中,不能判断四边形ABCD是平行四边形的是( )
A. AB=CD,BC=AD
B. AB∥CD,BC=AD
C. AB∥CD,BC∥AD
D. ∠A=∠C,∠B=∠D
B
4. (天门中考)在下列条件中能够判定一个四边形是平行四边形的是( )
A. 一组对边平行,另一组对边相等
B. 一组对边相等,一组对角相等
C. 一组对边平行,一条对角线平分另一条对角线
D. 一组对边相等,一条对角线平分另一条对角线
C
5. 如图,在△ABC和△DEC关于点C成中心对称,若AC= ,AB=1,∠BAC=90°,则AE的长是________.
6. 如图,已知DE是△ABC的中位线,F是DE上一点,若∠AFC=90°,DF=1,BC=10,求AC的长.
解 ∵ DE是△ABC的中位线,BC=10,
∴ DE= BC=5
∴ EF=DE-DF=5-1=4.
又∵ ∠AFC=90°,EF是△ACF的斜边AC上的中线,
∴ AC=2EF=2×4=8.
7. 如图,□ABCD的对角线相交于点O,直线MN经过点O,分别与AB ,CD交于点M,N ,连接AN,CM.
求证:AN=CM.
证明 ∵ AC,BD为□ABCD的对角线,且相交于点O,
∴ OA=OC.
∵ AB∥CD,
∴ ∠MAO=∠NCO.
又 ∠AOM=∠CON,
∴ △AOM≌△CON.
∴ OM=ON.
∴ 四边形AMCN是平行四边形.
∴ AN=CM.
课堂小结
三角形的中位线定理:三角形的中位线平行于第三边,并且等于第三边的一半.
多边形的内角和与外角和
内角和计算公式
(n-2) × 180 °(n ≥3的整数)
外角和
多边形的外角和等于360°
特别注意:与边数无关
正多
边形
内角= ,外角=
四边形的分类及转化
有一个角是90°
(或对角线相等)
有一对邻边相等
(或对角线互相垂直)
平行四边形
矩形
菱形
正方形
一组邻边相等且一个内角为直角
(或对角线互相垂直且相等)
有一个角是90°
(或对角线相等)
有一对邻边相等
(或对角线互相垂直)
课堂小结
湘教版·初中数学·八年级下册·第2章
第2章 四边形
复习课
复习目标
1.理解平行四边形、矩形、菱形、正方形概念之间的 联系和区别.
2.能用正方形的定义、性质和判定进行推理与计算.
3.掌握多边形内角和与外角和中心对称的性质与三角形中位线的性质并能应用。
学习重点:
根据具体问题情境,选择适当的知识进行推理计算.
。
1. n边形的内角和等于 。n边形的外角和等于 。
(n-2) ·180°
360°
②、中点 + = 中位线
2、三角形的中位线定理:
三角形的中位线平行于第三边,并且等于第三边的一半。
简单记忆
①、中点 + = 中位线
中点
平行
3、中心对称图形的特征
在成中心对称的两个图形中,对应点所连线段都经过 ,并且被对称中心________.
对称中心
平分
复习引入
一、多边形的内角和与外角和
多边形的内角和等于
多边形的外角和等于
正多边形每个内角的度数是
正多边形每个外角的度数是
要点梳理
(n-2) ×180 °
360 °
几 何 语 言
文字叙述
对边平行
对边相等
对角相等
∴ AD=BC ,AB=DC.
∵ 四边形ABCD是平行四边形,
∴ ∠ A=∠C,∠ B=∠D.
∵ 四边形ABCD是平行四边形,
二、平行四边形的性质
对角线互
相平分
∵ 四边形ABCD是平行四边形,
∴ OA=OC,OB=OD.
∵ 四边形ABCD是平行四边形,
∴ AD∥BC ,AB∥DC.
A
B
C
D
O
几 何 语 言
文字叙述
两组对边相等
一组对边平行且相等
∴四边形ABCD是平行四边形,
∵ AD=BC ,AB=DC.
∴ 四边形ABCD是平行四边形,
∵ AB=DC,AB∥DC.
三、平行四边形的判定
对角线互相平分
∴ 四边形ABCD是平行四边形,
∵ OA=OC,OB=OD.
两组对边分别平行(定义)
∴四边形ABCD是平行四边形,
∵ AD∥BC ,AB∥DC.
平行线之间的距离处处相等
A
B
C
D
O
1.中心对称
把一个图形绕着某一个点旋转____,如果它能与另一个图形重合,那么就说这两个图形成中心对称,这个点叫做对称中心,这两个图形中的对应点叫做关于中心的对称点.
180°
四、中心对称
1.三角形的中位线定义:连接三角形两边中点的线段叫做三角形的中位线.
2.三角形的中位线性质:三角形的中位线平行于第三边,并且等于第三边的一半.
五、三角形的中位线
用符号语言表示
∵DE是△ABC的中位线
∴DE∥BC,
平行且相等
平行
且四边相等
平行
且四边相等
四个角
都是直角
对角相等
邻角互补
四个角
都是直角
互相平分且相等
互相垂直平分且相等,每一条对角线平分一组对角
互相垂直且平分,每一条对角线平分一组对角
六、矩形、菱形、正方形的性质
①定义:有一内角是直角的平行四边形
②三个角是直角的四边形
③对角线相等的平行四边形
①定义:一组邻边相等的平行四边形
②四条边都相等的四边形
③对角线互相垂直的平行四边形
①定义:一组邻边相等且有一个角是直角的平行四边形
②有一组邻边相等的矩形
③有一个角是直角的菱形
七、矩形、菱形、正方形的判定方法
知识点1 多边形的内角和、外角和
1. n边形的内角和等于________________.
2. 任意多边形的外角和等于 _______.
3. 在平面内,_______________________的多边形叫作正多边形.
4. 三角形具有稳定性,四边形具有_____________.
(n-2)·180°
360°
边相等、角也相等
不稳定性
例1 一个正多边形的内角和为1080°,则这个正多边形的每一个外角等于( )
A. 30° B. 45°
C. 60° D. 72°
B
解析 设多边形的边数为n,则
(n-2)×180°=1080°,解得n=8.
它的每一个外角为360°÷8=45°,
故选B.
做一做 (莱芜中考)一个多边形的内角和比其外角和的2倍多180°,则该多边形的对角线的条数是( )
A. 12 B. 13
C. 14 D. 15
解析 设多边形的边数为n,则(n-2)×180°=360°×2+180°,解得n=7.该多边形的对角线的条数为7×(7 3)/2=14,故选C
C
注意 从n边形的一个顶点出发,有(n-3)条对角线把n边形分成(n-3)个三角形,其内角和公式由三角形的内角和得到.
重要提示
1. n边形有n个内角,每一个顶点处的一个外角与内角的和等于180°;
2. 正多边形的各个内角相等,各个外角相等;
3. 一般地,求多边形的内角和,直接利用外角和公式计算;求多边形的边数,利用n边形的外角和公式和外角和等于360°列出方程求解.
知识点2 平行四边形的性质
1. 平行四边形的对边_________________.
2. 平行四边形的对角_________,邻角__________.
3. 平行四边形的对角线____________________.
4. 平行四边形是__________对称图形,但不是_________对称图形.
平行且相等
相等
互补
互相平分
中心
轴
例2 如图,在□ABCD中,对角线AC,BD相交于点O,过点O任意作直线EF分别交AD,BC于点E,F.
(1) 求证:OE=OF.
(2) 若AB=EF=8,BC=10,求四边形EFCD的周长.
(1)证明 ∵ 四边形ABCD是平行四边形,∴ OA=OC,AD∥BC.
∴ ∠AEO=∠CFO,∠EAO=∠FCO.
∴ △AEO≌△AEO.
∴ OE=OF.
(2)解 ∵ △AEO≌△AEO,
∴ AE=CF.
又∵ AD=BC,即AE+DE=BF+CF.
∴ DE=BF.
∴ DE+CF=BF+CF=BC=10.
∵ AB=CD,AB=8.
∴ CD=8.
∴ 四边形EFCD的周长为DE+CF+EF+CD=10+8+8=26.
做一做 (侯马市期末)如图,在□ABCD中,AC,BD交于点O,AE⊥BD于点E,BD=20,BE=7,AE=4,则AC的长等于____________.
在Rt△AOE中,由勾股定理得
OA= ,从而
AC=2OA=10.
解析 ∵ 四边形ABCD是平行四边形,
BD=20,BE=7,
∴ OB= BD=10,OE=OB-BE=3.
10
重要提示
已知平行四边形解决角和线段的问题,要注意:
1. 根据平行四边形的性质,得出所需要的结论;
2. 用得到的结论作为条件,判定两个三角形全等,或判定一个三角形是等腰三角形或直角三角形等;
3. 利用三角形、全等三角形的性质解决问题;
4. 一条对角线把平行四边形分成两个全等的三角形,两条对角线把平行四边形分成两对全等的三角形.
知识点3 平行四边形的判定
1. 两组对边_____________的四边形叫作平行四边形.
2. 一组对边 _____________ 的四边形是平行四边形.
3. 两组对边_____________的四边形是平行四边形.
4. 两组对角_____________的四边形是平行四边形.
5. 对角线_______________的四边形是平行四边形.
分别平行
平行且相等
分别相等
分别相等
互相平分
例3 如图,在□ABCD中,E,F是对角线BD上的点,且DE=BF.
求证:四边形AECF是平行四边形.
思路1 运用判定定理“一组对边平行且相等的四边形是平行四边形”,先证AE∥CF,且AE∥CF.
思路2 运用判定定理“对角线互相平分的四边形是平行四边形”,连接AC,交BD与点O,则OA=OC,证OE=OF即可.
证法一 ∵ 四边形ABCD是平行四边形,
∴ AD=BC,AD∥BC.
∴ ∠ADE=∠CBF.
又∵ DE=BF,
∴ △ADE≌△CBF.
∴ AE=CF,∠AED=∠CFB.
∴ AE∥CF.
∴ 四边形AECF是平行四边形.
证法二 连接BD.
∵ 四边形ABCD是平行四边形,
∴ OA=OC,OB=OD.
又∵ BF=DE,
∴ BF-OB=DE-OD.
∴ OF=OE.
∴ 四边形AECF是平行四边形.
做一做 如图,在四边形ABCD中,BE平分∠ABC交DA于点E,AB=AE,添加下列条件,一定能判定四边形ABCD是平行四边形的是( )
A. AB=CD
B. AD=BC
C. BE=BC
D. ∠A=∠D
B
重要提示
平行四边形的判定,要注意:
1. 根据条件和问题,正确选择判定方法;
2. 要充分利用已知平行四边形或三角形的性质得到判定平行四边形的条件,必要时需添加辅助线如对角线等;
3. 注意推理严密,语言规范.
知识点4 中心对称与中心对称图形
1. 在平面内,如果一个图形G绕点O旋转 ________,得到的像与另一个图形G′重合,那么称这两个图形关于点O中心对称,点O叫作_____________.
2. 成中心对称的两个图形中,对应点的连线经过对称中心,并且被对称中心________.
3. 如果一个图形绕一个点O旋转180°,所得到的像与原来的图形重合,那么这个图形叫作_______________,这个点O叫作它的对称中心.
对称中心
180°
平分
中心对称图形
例4 如图,已知△ACE和△DBF是关于某一点成中心对称的两个图形,连接BE,CF.
(1) 作出对称中心.
(2) 求证:四边形BECF是平行四边形.
(1)解 连接EF,交BC于点O,则点O为△ACE和△DBF的对称中心.
(2)证明 ∵ 点B和点C,点E和点F分别是两个成中心对称三角形的对称点,
∴ OB=OC,OE=OF.
∴ 四边形BECF是平行四边形.
做一做 1. 下列图形中,是中心对称图形但不是轴对称图形的是( )
A. 平行四边形
B. 矩形
C. 菱形
D. 正六边形
A
2. 下列图形中,是轴对称图形但不是中心对称图形的是( )
C
重要提示
解决中心对称与中心对称图形问题,要注意:
1. 明确对称中心——两组对应点连线的交点;
2. 根据对应中心和对应点得出相等的线段(边)和角.
知识点5 三角形的中位线
1. 连接三角形两边 _______的线段叫作三角形的中位线.
2. 三角形的中位线__________第三边,并且等于_______________.
3. 过三角形一边的中点,并且平行于另一边的直线,一定
经过第三边的______.
中点
平行于
第三边的一半
中点
例5 如图,在△ABC中,点E,F,G分别是边AB,BC,CA的中点,AD⊥BC,AB=10,BD=8,CD=4.
(1)求证:∠EDG=∠EFG.
(2)求四边形ABCD的周长和
四边形AEDG的面积.
(1)证明 ∵ EF,FG是△ABC的中线,AD⊥BC,AB=6,
∴ EF∥AG,FG∥AE.
∴ 四边形ABCD是平行四边形.
∴∠EFG=∠EAG.
又∵ AD⊥BC,
∴ ∠ADB=∠ADC=90°.
∴ DE= AB=AE,DG= AC=AG.
∴ ∠DAE=∠ADE,∠DAG=∠ADG.
∴ ∠DAE+∠DAG=∠ADE+∠ADG,即∠EAG=∠EDG.
∴ ∠EFG==∠EDG.
(2)解 在Rt△ABD中,∠ADB=90°,AB=10,BD=8,根据勾股定理,得
AD=
在Rt△ACD中,∠ADC=90°,AD=6,CD=4,根据勾股定理,得 AC= .
∵ EF,FG是△ABC的中位线,四边形ABCD是平行四边形
∴ EF=AG= AC,FG=AE= AB.
∴ EF+AG+FG+AE=AB+AC=10+ .
即四边形ABCD的周长为10+ .
如图,连接EG,交AD为点O,则 EF是△ABC的中位线,
∴ EG= BC= (BD+DC)= (8+4)=6,EG∥BC.
又∵ AD⊥BC,
∴ AD⊥EG.
∴
= EG(AO+DO)= EG·AD= ×6× = .
做一做 如图,□ABCD的对角线AC,BD相交于点O,OE∥AB,下列判断中正确的是( )
A. AD=2OE
B. AC=2OE
C. BD=2OE
D. CD=2OE
D
重要提示
解决与三角形的中位线有关的问题,应注意:
1. 从数量和位置两个方面准确运用三角形的中位线性质;
2. 问题中如果有条件:已知三角形的中点,则可以尝试添加辅助线——三角形的中线或中位线解决问题.
考点一 多边形的内角和与外角和
例1:已知一个多边形的每个外角都是其相邻内角度数的 ,求这个多边形的边数.
解: 设此多边形的外角的度数为x,则内角的度数为4x,
则x+4x=180°,解得 x=36°.
∴边数n=360°÷36°=10.
考点讲练
1.一个正多边形的每一个内角都等于120 °,则其边数是 .
6
【解析】 因为该多边形的每一个内角都等于120°,所以它的每一个外角都等于60 °.所以边数是6.
归纳拓展
在多边形的有关求边数或内角、外角度数的问题中,要注意内角与外角之间的转化,以及定理的运用.尤其在求边数的问题中,常常利用定理列出方程,进而再求得边数.
针对训练
考点二 平行四边形的性质
例2 如图,在平行四边形ABCD中,下列结论中错误的是( )
A.∠1=∠2 B.∠BAD=∠BCD
C.AB=CD D.AC=BC
【解析】A.∵四边形ABCD是平行四边形,
∴AB∥CD,∴∠1=∠2,故A正确;
B.∵四边形ABCD是平行四边形,
∴∠BAD=∠BCD,故B正确;
C.∵四边形ABCD是平行四边形,
∴AB=CD,故C正确;
D
方法总结
主要考查了平行四边形的性质,关键是掌握平行四边形对边相等且平行,对角相等.
针对训练
2.如图,已知 ABCD中,AE平分∠BAD,CF平分∠BCD,分别交BC、AD于E、F.求证:AF=EC.
证明:∵四边形ABCD是平行四边形,
∴∠B=∠D,AD=BC,AB=CD,∠BAD=∠BCD,
(平行四边形的对角相等,对边相等)
∵AE平分∠BAD,CF平分∠BCD,
∴∠EAB= ∠BAD,∠FCD= ∠BCD,∴∠EAB= ∠FCD,
在△ABE和△CDF中
∠B=∠D
AB=CD ∴△ABE≌△CDF,∴BE=DF.
∠EAB=∠FCD
∵AD=BC ∴AF=EC.
例3 如图,在 ABCD中,∠ODA=90°,AC=10cm,BD=6cm,则AD的长为( )
A.4cm B.5cm C.6cm D.8cm
【解析】∵四边形ABCD是平行四边形,
AC=10cm,BD=6cm
∴OA=OC= AC=5cm,OB=OD= BD=3cm,
∵∠ODA=90°,
∴AD= =4cm.
A
方法总结
主要考查了平行四边形的性质,平行四边形的对角线互相平分,解题时还要注意勾股定理的应用.
【解析】∵在 ABCD中,对角线AC和BD交于点O,AC=24cm,BD=38cm,AD=28cm,
∴AO=CO=12cm,BO=19cm,AD=BC=28cm,
∴△BOC的周长是:BO+CO+BC=12+19+28=59(cm).
针对训练
3.如图,在 ABCD中,对角线AC和BD交于点O,AC=24cm,BD=38cm,AD=28cm,则△BOC的周长是( )
A.45cm B.59cm C.62cm D.90cm
B
考点三 平行四边形的判定
例4 如图,四边形ABCD的对角线交于点O,下列哪组条件不能判断四边形ABCD是平行四边形( )
A.OA=OC,OB=OD
B.∠BAD=∠BCD,AB∥CD
C.AD∥BC,AD=BC
D.AB=CD,AO=CO
D
平行四边形的判定方法:
①两组对边分别平行的四边形是平行四边形;
②两组对边分别相等的四边形是平行四边形;
③两组对角分别相等的四边形是平行四边形;
④对角线互相平分的四边形是平行四边形;
⑤一组对边平行且相等的四边形是平行四边形.
方法总结
考点四 中心对称及中心对称图形
例5 下列图形中,既是轴对称图形,又是中心对称图形的是( ).
A B C D
D
【解析】 图A.图B都是轴对称图形,图C是中心对称图形,图D既是中心对称图形也是轴对称图形.
考点五 三角形的中位线
例6 已知:AD是△ABC的中线,E是AD的中点,F是BE的延长线与AC的交点.求证: .
证明:过点D作DH∥BF,交AC于点H.
∵AD是△ABC的中线.
∴D是BC的中点.
∴CH=HF= CF
∵E是AD的中点,EF∥DH.
∴AF=FH.
∴AF= FC
A
B
C
D
E
F
H
例7:如图,在矩形ABCD中,两条对角线相交于点O,
∠AOD=120°,AB=2.5 ,求矩形对角线的长.
解:∵四边形ABCD是矩形.
∴AC = BD(矩形的对角线相等).
OA= OC= AC,OB = OD = BD ,
(矩形对角线相互平分)
∴OA = OD.
A
B
C
D
O
考点六 矩形的性质和判定
A
B
C
D
O
∵∠AOD=120°,
∴∠ODA=∠OAD= (180°- 120°)=30°.
又∵∠DAB=90° ,
(矩形的四个角都是直角)
∴BD = 2AB = 2 ×2.5 = 5.
例8:如图,在菱形ABCD中,对角线AC与BD相交于点O,∠BAD=60°,BD =6,求菱形的边长AB和对角线AC的长.
解:∵四边形ABCD是菱形,
∴AC⊥BD(菱形的对角线互相垂直)
OB=OD= BD = ×6=3(菱形的对角线互相平分)
在等腰三角形ABC中,
∵∠BAD=60°,
∴△ABD是等边三角形.
∴AB = BD = 6.
∴在Rt△AOB中,AO
∴AC=2AO=
A
B
C
O
D
考点七 菱形的性质和判定
巩固练习
1. 一个正多边形的内角和是1260°,则它的每一个外角的度数等于( )
A. 30°
B. 40°
C. 60°
D. 72°
B
2. 如图,在□ABCD中,对角线AC,BD相交于点O,下列说法中不正确的是( )
A. AB=CD
B. OB=OD
C. ∠ABD=∠DCA
D. ∠BAD+∠ADC=180°
C
3. 如图,下列条件中,不能判断四边形ABCD是平行四边形的是( )
A. AB=CD,BC=AD
B. AB∥CD,BC=AD
C. AB∥CD,BC∥AD
D. ∠A=∠C,∠B=∠D
B
4. (天门中考)在下列条件中能够判定一个四边形是平行四边形的是( )
A. 一组对边平行,另一组对边相等
B. 一组对边相等,一组对角相等
C. 一组对边平行,一条对角线平分另一条对角线
D. 一组对边相等,一条对角线平分另一条对角线
C
5. 如图,在△ABC和△DEC关于点C成中心对称,若AC= ,AB=1,∠BAC=90°,则AE的长是________.
6. 如图,已知DE是△ABC的中位线,F是DE上一点,若∠AFC=90°,DF=1,BC=10,求AC的长.
解 ∵ DE是△ABC的中位线,BC=10,
∴ DE= BC=5
∴ EF=DE-DF=5-1=4.
又∵ ∠AFC=90°,EF是△ACF的斜边AC上的中线,
∴ AC=2EF=2×4=8.
7. 如图,□ABCD的对角线相交于点O,直线MN经过点O,分别与AB ,CD交于点M,N ,连接AN,CM.
求证:AN=CM.
证明 ∵ AC,BD为□ABCD的对角线,且相交于点O,
∴ OA=OC.
∵ AB∥CD,
∴ ∠MAO=∠NCO.
又 ∠AOM=∠CON,
∴ △AOM≌△CON.
∴ OM=ON.
∴ 四边形AMCN是平行四边形.
∴ AN=CM.
课堂小结
三角形的中位线定理:三角形的中位线平行于第三边,并且等于第三边的一半.
多边形的内角和与外角和
内角和计算公式
(n-2) × 180 °(n ≥3的整数)
外角和
多边形的外角和等于360°
特别注意:与边数无关
正多
边形
内角= ,外角=
四边形的分类及转化
有一个角是90°
(或对角线相等)
有一对邻边相等
(或对角线互相垂直)
平行四边形
矩形
菱形
正方形
一组邻边相等且一个内角为直角
(或对角线互相垂直且相等)
有一个角是90°
(或对角线相等)
有一对邻边相等
(或对角线互相垂直)
课堂小结
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
