专题1.1 平分---倍长中线模型 课件(共15张PPT)-中考数学二轮复习必会几何模型剖析(全国通用)
文档属性
| 名称 | 专题1.1 平分---倍长中线模型 课件(共15张PPT)-中考数学二轮复习必会几何模型剖析(全国通用) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-25 06:53:08 | ||
图片预览





文档简介
(共15张PPT)
专题一 平分模型
§1.1 与“中点”有关的模型
人教版中考第二轮总复习---几何模型
倍长中线模型
01
倍长类中线模型
02
03
知识要点
精讲精练
目录
图形示例 考查题型 模型分析 解题原理
三角形(3次) 正方形(2次) 菱形(1次)
考点6-1
模型分析
倍长中线模型
A
D
C
B
E
(1)以线段拼成三角形为背景考查新定义问题,倍长中线证明线段数量关系;
(2)以正方形为背景,结合图形旋转,证明线段数量关系;
(3)以一般三角形为背景,作倍长中线或平行倍长中线,
当已知条件中出现中线时,常常将此中线倍长构造全等三角形解决问题.
如图,在△ABC中,D为BC的中点,
延长AD到点E,使DE=AD,连接BE,则△ADC≌△EDB
找到三角形中线,倍长中线证明8字形三角形全等,从而得到线段数量关系.
【例1】如图,在△ABC中,AD是BC边上的中线,E是AD上一点,延长BE交AC于点F,AF=EF,求证:AC=BE.
②延长ED到点G,使得DG=DE,构造△CGD全等于△BED.
【思 考 】 你 能 想 到 哪 些 作 辅 助 线 的 方 法 :
①延长AD到点G,使得DG=AD,构造△GDB全等于△ADC;
A
F
C
D
B
E
G
证法一:如图,延长AD到点G,使得DG=AD,连接BG.
∵点D是BC的中点.
∴BD=CD.
∵∠BDG=∠CDA.AD=GD.
∴△ADC≌△GDB.
∴AC=GB.∠G=∠EAF.
∵AF=EF.
∴∠EAF=∠AEF.
∵∠AEF=∠BED.
∴∠G=∠BED.
∴BE=BG.
∴BE=AC.
考点6-1
典例精讲
倍长中线模型
A
F
C
D
B
E
G
∴AC=BE.
证法二:如解图②,延长ED到点G,使得DG=DE,连接CG.
∵点D是BC的中点.
∴BD=CD.
∵∠BDE=∠CDG,DG=DE.
∴△BED≌△CGD.
∴∠G=∠BED,BE=CG.
∵AF=EF.
∴∠FAE=∠AEF=∠BEG.
∴∠G=∠EAF.
∴AC=GC.
考点6-1
典例精讲
倍长中线模型
考点6-2
模型分析
倍长类中线模型
图形示例 模型分析
当已知条件中出现类中线(中点有关的线段)时,常常利用倍长类中线倍长构造全等三角形解决问题.
如图,在△ABC中,D为BC的中点,点E在AB上(不与点A,B重合),
A
D
C
B
E
F
延长ED到点F,使DF=ED,连接CF,则有△BED≌△CFD
A
D
C
E
B
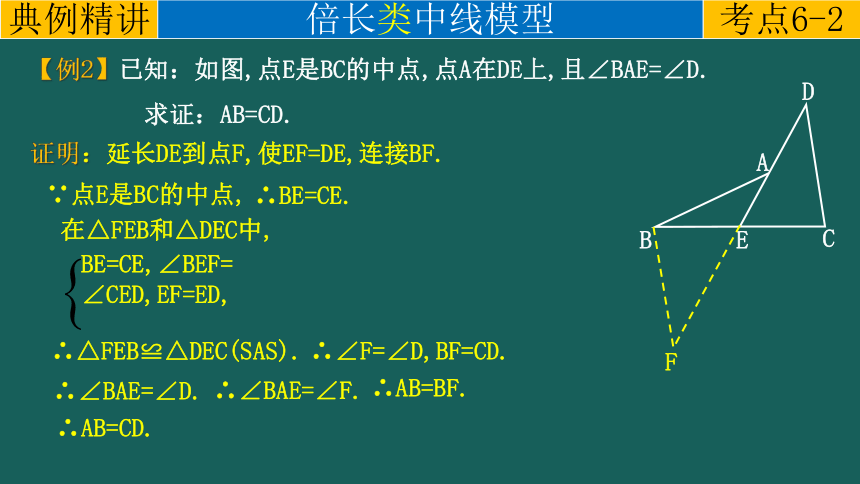
【例2】已知:如图,点E是BC的中点,点A在DE上,且∠BAE=∠D.
求证:AB=CD.
证明:延长DE到点F,使EF=DE,连接BF.
F
∵点E是BC的中点,
∴BE=CE.
在△FEB和△DEC中,
BE=CE,∠BEF=∠CED,EF=ED,
∴AB=CD.
∴△FEB≌△DEC(SAS).
∴∠F=∠D,BF=CD.
∴∠BAE=∠D.
∴∠BAE=∠F.
∴AB=BF.
考点6-2
典例精讲
倍长类中线模型
知识梳理
课堂小结
中点问题常用性质及常见辅助线作法
2.一边的垂线过这边中点
垂直平分线性质;
1.中线或与中点有关线段
中线倍长构造全等;
3.圆+弦或弧的中点
垂径定理或圆周角定理.
联想
联想
联想
联想
6.多个中点或平行+中点
4.直角三角形+斜边中点
5.等腰三角形+底边中点
构造中位线;
直角三角形斜边中线性质;
等腰三角形三线合一;
联想
联想
1.已知:如图,在△ABC中,AD是BC边上的中线,E是AD上一点,且BE=AC,延长BE交AC于点F.求证:AF=EF.
A
D
C
F
B
E
∴△ADC≌GDB(SAS)
证明:延长AD到点G,使得DG=AD,连接BG.
∵AD是BC边上的中线,
∴DC=DB.
在△ADC和△GDB中
AD=GD,∠ADC=∠GDB,DC=DB,
G
∴AF=EF.
∴∠CAD=∠G,AC=BG.
∵BE=AC.
∴BE=BG.
∴∠BED=∠G.
∵∠BED=∠AEF.
∴∠AEF=∠G.
∴∠AEF=∠CAD,
即∠AEF=∠FAE.
知识点一
针对训练
倍长中线模型
2.如图,在四边形ABCD中,∠A+∠B=90 ,AD=6,BC=8,点E为AB的中点,DE⊥CE,求CD的长.
知识点一
针对训练
倍长中线模型
F
A
C
D
E
B
证明:延长CE到点F,使得EF=CE,连接AF,DF.
∵点E为BC的中点,
∴AE=BE.
∵∠AEF=∠BEC,
∴△AEF≌BEC(SAS)
∴AF=BC=8,∠FAE=∠B.
∵∠A+∠B=90 .
∴∠A+∠FAE=90 .即∠FAD=90 .
由勾股定理得:
DF=
AF2+AD2
= 82+62
=10
∵DE⊥CE,EF=CE.
∴CD=DF=10.
3.E是BC中点,EF∥DA,若BG=CF,求证:AD平分∠BAC.
解:延长FE到点H,使EH=EF,连接BH.
∴AD平分∠BAC
在△FEC和△HEB中
FE=HE
∠1=∠2
CE=BE
∴△FEC≌△HEB(SAS)
∴∠H=∠F,BH=CF
∵BG=CF,
∴BG=BH,
∴∠H=∠3=∠4=∠F
∵EF∥AD
∴∠4=∠6,∠F=∠5
∴∠5=∠6
B
C
D
E
A
G
F
H
1
2
3
4
5
6
知识点一
针对训练
倍长类中线模型
3.如图,在△ABC中,AB=3,AC=5,则BC边上中线AD的范围是_________.
提升能力
强化训练
中点问题的常见模型
E
2<AD<8
C
D
B
A
图3
10.如图,CB是△AEC中线,CD是△ABC中线,AC=AB.
求证:(1)2CD=CE; (2)CB平分∠DCE.
A
E
C
B
D
F
提升能力
强化训练
中点问题的常见模型
13.在△ABC中,D为BC的中点.
(1)如图1,AB=5,AC=3,AD=2,求△ABC的面积;
图1
D
C
B
A
E
(1)解:如解图1,延长AD至点E,使得DE=AD,连接BE,CE.
∵BD=DC,DE=AD.
∴四边形ABEC是平行四边形.
∴BE=AC=3,AE=2AD=4.
在△ABE中,三条边的长度3、4、5是勾股数.
∴△ABE是直角三角形.
∴S△ABE=1/2×3×4=6.
根据平行四边形的性质可知S△ABC=S△ABE.
∴S△ABC=6;
提升能力
强化训练
中点问题的常见模型
(2)如图2,M为AC的中点,连接BM交AD于点F,若AM=MF.
求证:BF=AC.
A
F
M
D
C
B
图2
(2)证明:如图2,延长AD至点E,使DE=AD,连接BE,CE.
∵BD=DC,DE=AD.
∴四边形ABEC是平行四边形.
∴AC=BE,AC∥BE.
∴∠MAF=∠BEA.
∵AM=MF,
∴∠MAF=∠AFM.
∵∠BFE=∠MFA,
∴∠BEF=∠BFE.
∴BF=BE.
∴BF=AC.
E
提升能力
强化训练
中点问题的常见模型
专题一 平分模型
§1.1 与“中点”有关的模型
人教版中考第二轮总复习---几何模型
倍长中线模型
01
倍长类中线模型
02
03
知识要点
精讲精练
目录
图形示例 考查题型 模型分析 解题原理
三角形(3次) 正方形(2次) 菱形(1次)
考点6-1
模型分析
倍长中线模型
A
D
C
B
E
(1)以线段拼成三角形为背景考查新定义问题,倍长中线证明线段数量关系;
(2)以正方形为背景,结合图形旋转,证明线段数量关系;
(3)以一般三角形为背景,作倍长中线或平行倍长中线,
当已知条件中出现中线时,常常将此中线倍长构造全等三角形解决问题.
如图,在△ABC中,D为BC的中点,
延长AD到点E,使DE=AD,连接BE,则△ADC≌△EDB
找到三角形中线,倍长中线证明8字形三角形全等,从而得到线段数量关系.
【例1】如图,在△ABC中,AD是BC边上的中线,E是AD上一点,延长BE交AC于点F,AF=EF,求证:AC=BE.
②延长ED到点G,使得DG=DE,构造△CGD全等于△BED.
【思 考 】 你 能 想 到 哪 些 作 辅 助 线 的 方 法 :
①延长AD到点G,使得DG=AD,构造△GDB全等于△ADC;
A
F
C
D
B
E
G
证法一:如图,延长AD到点G,使得DG=AD,连接BG.
∵点D是BC的中点.
∴BD=CD.
∵∠BDG=∠CDA.AD=GD.
∴△ADC≌△GDB.
∴AC=GB.∠G=∠EAF.
∵AF=EF.
∴∠EAF=∠AEF.
∵∠AEF=∠BED.
∴∠G=∠BED.
∴BE=BG.
∴BE=AC.
考点6-1
典例精讲
倍长中线模型
A
F
C
D
B
E
G
∴AC=BE.
证法二:如解图②,延长ED到点G,使得DG=DE,连接CG.
∵点D是BC的中点.
∴BD=CD.
∵∠BDE=∠CDG,DG=DE.
∴△BED≌△CGD.
∴∠G=∠BED,BE=CG.
∵AF=EF.
∴∠FAE=∠AEF=∠BEG.
∴∠G=∠EAF.
∴AC=GC.
考点6-1
典例精讲
倍长中线模型
考点6-2
模型分析
倍长类中线模型
图形示例 模型分析
当已知条件中出现类中线(中点有关的线段)时,常常利用倍长类中线倍长构造全等三角形解决问题.
如图,在△ABC中,D为BC的中点,点E在AB上(不与点A,B重合),
A
D
C
B
E
F
延长ED到点F,使DF=ED,连接CF,则有△BED≌△CFD
A
D
C
E
B
【例2】已知:如图,点E是BC的中点,点A在DE上,且∠BAE=∠D.
求证:AB=CD.
证明:延长DE到点F,使EF=DE,连接BF.
F
∵点E是BC的中点,
∴BE=CE.
在△FEB和△DEC中,
BE=CE,∠BEF=∠CED,EF=ED,
∴AB=CD.
∴△FEB≌△DEC(SAS).
∴∠F=∠D,BF=CD.
∴∠BAE=∠D.
∴∠BAE=∠F.
∴AB=BF.
考点6-2
典例精讲
倍长类中线模型
知识梳理
课堂小结
中点问题常用性质及常见辅助线作法
2.一边的垂线过这边中点
垂直平分线性质;
1.中线或与中点有关线段
中线倍长构造全等;
3.圆+弦或弧的中点
垂径定理或圆周角定理.
联想
联想
联想
联想
6.多个中点或平行+中点
4.直角三角形+斜边中点
5.等腰三角形+底边中点
构造中位线;
直角三角形斜边中线性质;
等腰三角形三线合一;
联想
联想
1.已知:如图,在△ABC中,AD是BC边上的中线,E是AD上一点,且BE=AC,延长BE交AC于点F.求证:AF=EF.
A
D
C
F
B
E
∴△ADC≌GDB(SAS)
证明:延长AD到点G,使得DG=AD,连接BG.
∵AD是BC边上的中线,
∴DC=DB.
在△ADC和△GDB中
AD=GD,∠ADC=∠GDB,DC=DB,
G
∴AF=EF.
∴∠CAD=∠G,AC=BG.
∵BE=AC.
∴BE=BG.
∴∠BED=∠G.
∵∠BED=∠AEF.
∴∠AEF=∠G.
∴∠AEF=∠CAD,
即∠AEF=∠FAE.
知识点一
针对训练
倍长中线模型
2.如图,在四边形ABCD中,∠A+∠B=90 ,AD=6,BC=8,点E为AB的中点,DE⊥CE,求CD的长.
知识点一
针对训练
倍长中线模型
F
A
C
D
E
B
证明:延长CE到点F,使得EF=CE,连接AF,DF.
∵点E为BC的中点,
∴AE=BE.
∵∠AEF=∠BEC,
∴△AEF≌BEC(SAS)
∴AF=BC=8,∠FAE=∠B.
∵∠A+∠B=90 .
∴∠A+∠FAE=90 .即∠FAD=90 .
由勾股定理得:
DF=
AF2+AD2
= 82+62
=10
∵DE⊥CE,EF=CE.
∴CD=DF=10.
3.E是BC中点,EF∥DA,若BG=CF,求证:AD平分∠BAC.
解:延长FE到点H,使EH=EF,连接BH.
∴AD平分∠BAC
在△FEC和△HEB中
FE=HE
∠1=∠2
CE=BE
∴△FEC≌△HEB(SAS)
∴∠H=∠F,BH=CF
∵BG=CF,
∴BG=BH,
∴∠H=∠3=∠4=∠F
∵EF∥AD
∴∠4=∠6,∠F=∠5
∴∠5=∠6
B
C
D
E
A
G
F
H
1
2
3
4
5
6
知识点一
针对训练
倍长类中线模型
3.如图,在△ABC中,AB=3,AC=5,则BC边上中线AD的范围是_________.
提升能力
强化训练
中点问题的常见模型
E
2<AD<8
C
D
B
A
图3
10.如图,CB是△AEC中线,CD是△ABC中线,AC=AB.
求证:(1)2CD=CE; (2)CB平分∠DCE.
A
E
C
B
D
F
提升能力
强化训练
中点问题的常见模型
13.在△ABC中,D为BC的中点.
(1)如图1,AB=5,AC=3,AD=2,求△ABC的面积;
图1
D
C
B
A
E
(1)解:如解图1,延长AD至点E,使得DE=AD,连接BE,CE.
∵BD=DC,DE=AD.
∴四边形ABEC是平行四边形.
∴BE=AC=3,AE=2AD=4.
在△ABE中,三条边的长度3、4、5是勾股数.
∴△ABE是直角三角形.
∴S△ABE=1/2×3×4=6.
根据平行四边形的性质可知S△ABC=S△ABE.
∴S△ABC=6;
提升能力
强化训练
中点问题的常见模型
(2)如图2,M为AC的中点,连接BM交AD于点F,若AM=MF.
求证:BF=AC.
A
F
M
D
C
B
图2
(2)证明:如图2,延长AD至点E,使DE=AD,连接BE,CE.
∵BD=DC,DE=AD.
∴四边形ABEC是平行四边形.
∴AC=BE,AC∥BE.
∴∠MAF=∠BEA.
∵AM=MF,
∴∠MAF=∠AFM.
∵∠BFE=∠MFA,
∴∠BEF=∠BFE.
∴BF=BE.
∴BF=AC.
E
提升能力
强化训练
中点问题的常见模型
同课章节目录
