专题1.2 平分---中点问题的常见模型 课件(共22张PPT)-中考数学二轮复习必会几何模型剖析(全国通用)
文档属性
| 名称 | 专题1.2 平分---中点问题的常见模型 课件(共22张PPT)-中考数学二轮复习必会几何模型剖析(全国通用) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-25 06:50:59 | ||
图片预览








文档简介
(共22张PPT)
专题一 平分模型
专题1.1 与“中点”有关的模型
人教版中考第二轮总复习---几何模型
A
E
D
C
B
A
E
D
C
B
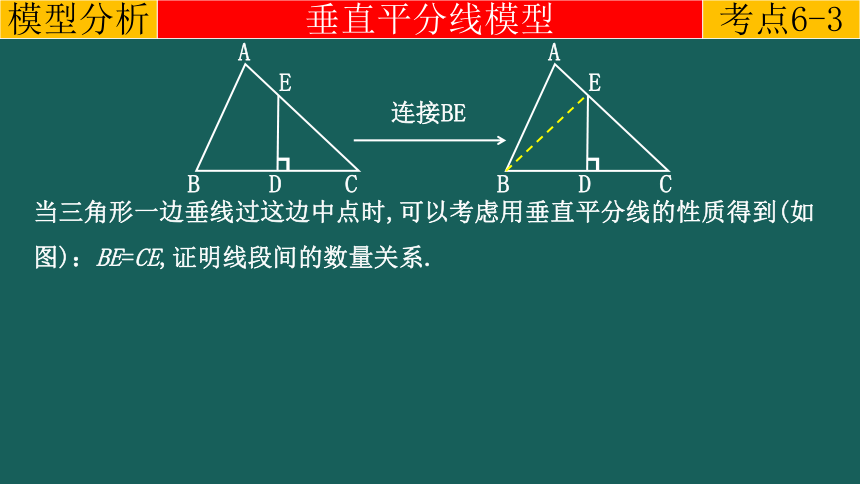
连接BE
当三角形一边垂线过这边中点时,可以考虑用垂直平分线的性质得到(如图):BE=CE,证明线段间的数量关系.
考点6-3
模型分析
垂直平分线模型
【例3】如图,在Rt△ABC中,∠ACB=90 ,BC=3,AC=4,点D是AB的中点,过点D作DE⊥AB交BC的延长线于点E,则CE的长为_____.
A
E
C
B
D
【思考】点D是AB的中点且DE⊥AB,你想到了哪些学过的知识:
______________________________________________________________.
DE是线段AB的垂直平分线,垂直平分线上的点到线段两端点的距离相等
设CE=x,连接AE.
∵DE是线段AB的垂直平分线.
∴AE=BE=BC+CE=3+x.
∴在Rt△ACE中,AE2=AC2+CE2.
即(3+x)2=42+x2,
考点6-3
典例精讲
垂直平分线模型
7
6
解得x=
7
6
图形示例 模型分析
在直角三角形中,当遇见斜边中点时,经常会作斜边上的中线,利用直角三角形斜边上的中线等于斜边的一半,即CD=0.5AB来证明线段间的数量关系,而且可以得到两个等腰三角形:△ACD和△BCD,该模型经常会与中位线定理一起综合应用.
B
C
A
D
考点6-4
模型分析
直角三角形的斜边中线模型
【思考】在直角三角形中遇到斜边上的中点,你想到了哪些学过的知识:___________________________________.
直角三角形斜边的中线等于斜边的一半
【例4】如图,∠ACB=90 ,点D为AB的中点,连接DC并延长到E,使CE=CD,过点B作BF∥DE,与AE的延长线交于点F,若BF=8,则AB的长度为____.
6
F
C
E
D
B
A
解:如图,∵BF∥DE,点D是AB的中点.
∴ED是△AFD的中位线.
∴BF=2ED=8.
∴ED=CE+CD=4.
∵∠ACB=90 ,D为AB的中点.
∴CD= 0.5AB.
∵CE=1/3CD.
∴AB=6.
考点6-4
典例精讲
直角三角形的斜边中线模型
图形示例 模型分析
当出现等腰三角形时,常隐含有底边中点,可利用其“三线合一”的性质.如图,在△ABC中,
(1)AC=BC;(2)CD平分∠ACB;(3)AD=BD;(4)CD⊥AB.
“知二得二”:比如由(2)(3)可得出(1)(4),也就是说,以上四条语句,任意选择两个作为条件,就可以推出剩下的两条.
A
D
C
B
考点6-5
模型分析
等腰三角形三线合一模型
【思考】在等腰三角形中遇到底边上的中点,你想到了哪些学过的知识:__________________________________________________.
【例5】如图,在△ABC中,AB=AC=5,BC=6,点M为BC的中点,MN⊥AC于点N.则MN的长为____.
A
B
N
M
C
等腰三角形底边中线、高线、顶角平分线“三线合一”
如图,连接AM.
∵AB=AC=5,点M为BC的中点.
∴AM⊥CM.
∵ 0.5AM×MC=0.5AC×MN.
考点6-5
典例精讲
等腰三角形三线合一模型
12
5
∴AM= 52-32=4
∴MN=
AM·CM
AC
12
5
=
图形示例 模型分析
当已知条件中同时出现两个及两个以上中点时,常考虑构造中位线;或出现一个中点,要证明平行线段或线段倍分关系时也常考虑构造中位线.利用三角形中位线的性质定理:DE∥BC,且DE=0.5BC,△ADE∽△ABC,则可得线段之间的相等或比例关系.
A
E
D
C
B
“角平分线,中点,垂直”只要出现了两个条件,考虑补全为等腰三角形三线合一模型.
考点6-6
模型分析
三角形中位线模型
【思考】在一般三角形中看到中点,你想到了哪些学过的知识:
_____________________________________________________________.
过中点作平行线可构造中位线,中位线平行于底边且等于底边的一半.
【例6】如图,M是△ABC的边BC的中点,AN平分∠BAC,BN⊥AN于点N,且AB=8,MN=3.则AC的长为( )A.3 B.7 C.8 D.14
D
A
N
M
C
B
D
∴AC=AD+DC=8+6=14.
解析:∵AN平分∠BAC.
∴∠BAN=∠DAN,AN=AN,∠ANB=∠AND=90 .
∴△ABN≌△AEN.
∴AD=AB=8,BN=ND.
∵M是△ABC的边BC的中点.
∴CD=2MN=2×3=6.
考点6-6
典例精讲
三角形中位线模型
知识梳理
课堂小结
中点问题常用性质及常见辅助线作法
2.一边的垂线过这边中点
垂直平分线性质;
1.中线或与中点有关线段
中线倍长构造全等;
3.圆+弦或弧的中点
垂径定理或圆周角定理.
联想
联想
联想
联想
6.多个中点或平行+中点
4.直角三角形+斜边中点
5.等腰三角形+底边中点
构造中位线;
直角三角形斜边中线性质;
等腰三角形三线合一;
联想
联想
A
N
M
D
B
C
1.如图,在四边形ABCD中,M,N分别是CD,BC的中点,且AM⊥CD,AN⊥BC.
(1)求证:∠BAD=2∠MAN;
(2)连接BD,若∠MAN=70 ,∠DBC=40 ,求∠ADC.
1
2
3
4
(1)证明:如解图,连接AC.
∵M是CD的中点,AM⊥CD.
∴AM是线段CD的垂直平分线.
∴AC=AD.
∵AM⊥CD.
∴∠3=∠4.
同理可得∠1=∠2.
(2)解:∵AM⊥CD,AN⊥BC,∠MAN=70 .
∴∠BCD=360 -90 -90 -70 =110 .
∴∠BDC=180 -∠DBC-∠BCD=30 ,∠BAD=2∠MAN=140 .
∵AB=AC,AD=AC.
∴AB=AD.
∴∠ADB=∠ABD=20 .
∴∠ADC=∠ADB+∠BDC=50 .
知识点二
针对训练
垂直平分线模型
2.如图,已知AB=24,AB⊥BC于点B,AB⊥AD于点A,AD=10,BC=20.若点E是CD的中点,则AE的长是_____.
13
A
C
B
E
D
知识点二
针对训练
垂直平分线模型
如图,在Rt△ABC中,∠ACB=90 ,CD为AB边上的高,若点A关于CD所在直线的对称点E恰好为AB的中点,则∠BCE的度数是( )
A.60 B.45 C.30 D.75
C
C
D
E
A
B
∵在Rt△ABC中,∠ACB=90 ,CD为AB边上的高,
点A关于CD所在直线的对称点E恰好为AB的中点.
∴∠CED=∠A,CE=BE=AE.
∴∠ECA=∠A,∠B=∠BCE.
∴△ACE是等边三角形.
∴∠CED=60 .
∴∠B=∠CED=30 .
∴∠A=60 .
知识点三
针对训练
直角三角形的斜边中线模型
如图,在矩形ABCD中,点E为AB边上一点,EC平分∠DEB,点F为CE的中点,连接AF,BF.过点E作EH∥BC分别交AF,CD于G,H两点.
求证:(1)DE=DC;(2)AF⊥BF.
A
M
H
D
C
B
E
F
G
证明:(1)∵四边形ABCD是矩形
∴AB∥CD.
∴∠DCE=∠CEB.
∵EC平分∠DEB.
∴∠DCE=∠CEB.
∴∠DCE=∠DEC.
∴DE=DC.
(2)连接DF.
∵DE=DC,点F为CE的中点,
∴DF⊥EC.
∴∠DFC=90 .
在矩形ABCD,AB=DC,∠ABC=90 ,
∴BF=CF=EF=0.5EC
∴∠ABF=∠CEB.
∵∠DCE=∠CEB,
∴∠ABF=∠DCF.
在△ABF和△DCF中
BF=CF
∠ABF=∠DCFAB=DC
∴△ABF≌△DCF(SAS)
∴∠AFB=∠DFC=90
∴AF⊥BF.
知识点四
针对训练
等腰三角形三线合一模型
在△ABC中,CD平分∠ACB,AD⊥CD,E是AB中点,AC=15,BC=27,求DE的长.
等腰中,造三线,两个条件快补全.
三线合一+中位线
F
【分析】本题中,点E已经是AB的中点,由CD平分∠ACB,
AD⊥CD,想到可以构造等腰三角形,利用三线合一,使点D成为另一个中点,从而让ED变成“看得见”的中位线.
∴DE=0.5BF=0.5(BC-CF)=0.5(BC-AC)=6.
解:延长AD交BC于F.
∵CD平分∠ACB,AD⊥CD
∴∠ACD=∠FCD,∠ADC=∠FDC=90 ,
∴∠CAD=∠CFD
∴AC=CF,AD=FD
∵E是AB的中点,D是FA的中点.
∴DE是△ABF的中位线,
知识点五
针对训练
三角形中位线模型
A
D
E
C
B
1.如图1,在△ABC中,AB=AC,A=30 ,AB的垂直平分线l交AC于点D,则∠CBD的度数为( ) A.30 B.45 C.50 D.75
2.如图2,在 Rt△ABC中,∠ACB=90°,点D,E分别是边AB,AC的中点,延长BC至点F,使CF=0.5BC,若AB=10,则EF的长是____.
B
A
F
E
D
B
C
图2
5
提升能力
强化训练
中点问题的常见模型
A
l
D
C
B
图1
4.如图,D是△ABC内一点,BD⊥CD,AD=12,BD=8,CD=6,点E,F,G,H分别是AB,
AC,CD,BD的中点,则四边形EFGH的周长是____.
5.如图,△ABC的面积是12,点D,E,F,G分别是BC,AD,BE,CE的中点,则△AFG的面积是____.
6.如图,在Rt△ABC中,D为斜边AC的中点,E为BD上一点,F为CE的中点.若AE=AD,DF=2,则BD的长为____.
22
4.5
A
D
G
H
F
E
C
B
A
G
F
D
C
B
E
提升能力
强化训练
中点问题的常见模型
4
A
F
E
D
C
B
7.如图,点M是△ABC的边BC的中点,AN平分∠BAC,BN⊥AN于点N,延长BN交AC于点D,已知AB=10,AC=16,则MN=____.
8.如图,在△ABC中,D是AB上一点,AD=AC,AE平分∠CAD,交CD于点E,F是BC的中点,若BD=16,则EF的长为____.
9.如图,在△ABC中,AB=8,AC=6,AD,AE分别是其角平分线和中线,点C作CG⊥AD于点F,交AB于点G,连接EF,则线段EF的长为____.
3
A
N
D
C
M
B
8
C
F
E
B
D
A
1
A
D
E
C
B
G
F
提升能力
强化训练
中点问题的常见模型
11.如图,在△ABC中,若∠B=2∠C,AD⊥BC,E为BC边中点,求证:AB=2DE.
F
EF为中位线,综合已知条件易得:DE=DF
A
E
D
C
B
提升能力
强化训练
中点问题的常见模型
【变式】如图,在△ABC中,AB=2,AC=3,E为BC的中点,AD平分∠BAC,CF⊥AD交AD的延长线于点F,求EF的长.
B
D
E
F
C
A
P
A
E
D
C
B
F
A
B
E
D
C
12.如图,在Rt△ABC中,∠ACB=90 ,CD为AB边上的高,CE为AB边上的中线,AD=4,CE=10,求CD的长.
解:在Rt△ABC中∠ACB=90 ,CE为AB边上的中线,CE=10,
∴AE=CE=10.
∵AD=4,
∴DE=6.
∵CD为AB边上的高,
∴在Rt△CDE中,
提升能力
强化训练
中点问题的常见模型
CD=
CE2-DE2
= 102-62=8.
14.如图,在平行四边形ABCD中,AC⊥BC,点E,F分别在AB,BC上,且满足AC=AE=CF,连接CE,AF,EF.
(1)若∠ABC=35°,求∠EAF的度数;
(2)若CE⊥EF,求证:CE=2EF.
A
E
B
F
C
D
M
∴CE=2EF.
(1)解:∵AC⊥BC,AC=CF.
∴△ACF为等腰直角三角形,则∠AFC=45 .
∵∠AFC=∠B+∠EAF,∠B=35 .
∴∠EAF=10 ;
(2)证明:如解图①,取CF的中点M,连接EM、AM.
∵CE⊥EF
∴EM=CM=FM=0.5CF.
∵AC=AE,
∴AM为EC的中垂线.
∴∠CAM+∠ACE=90 .
∵∠ECF+∠ACE=90 .
∴∠CAM=∠FCE.
∵∠CEF=∠ACM=90 .
∴△ACM∽△CEF.
∵CF=AC=2CM.
∴AC:CM=CE:EF=2:1
∴AC:CM=CE:EF
提升能力
强化训练
中点问题的常见模型
15.如图,在△ABC中,AD是高,CE是中线,点G是CE的中点,DG⊥CE于点G.
(1)求证:DC=BE;
(2)若∠AEC=66 ,求∠BCE的度数.
A
G
E
D
C
B
(1)证明:连接DE.
∵AD⊥BC,
∴∠ADB=90 .
∵AE=BE.
∴DE=BE=AE.
∵DG⊥EC,点G是CE的中点.
∴DE=CD.
∴DC=BE.
(2)解:设∠BCE=x.
∵BE=DE=DC,
∴∠DEC=∠DCE=x.
∴∠EBD=∠BDE=∠DEC+∠DCE=2x.
∵∠AEC=∠EBD+∠ECD,
∴66 =3x.
∴x=22 .
∴∠BCE=22 .
提升能力
强化训练
中点问题的常见模型
专题一 平分模型
专题1.1 与“中点”有关的模型
人教版中考第二轮总复习---几何模型
A
E
D
C
B
A
E
D
C
B
连接BE
当三角形一边垂线过这边中点时,可以考虑用垂直平分线的性质得到(如图):BE=CE,证明线段间的数量关系.
考点6-3
模型分析
垂直平分线模型
【例3】如图,在Rt△ABC中,∠ACB=90 ,BC=3,AC=4,点D是AB的中点,过点D作DE⊥AB交BC的延长线于点E,则CE的长为_____.
A
E
C
B
D
【思考】点D是AB的中点且DE⊥AB,你想到了哪些学过的知识:
______________________________________________________________.
DE是线段AB的垂直平分线,垂直平分线上的点到线段两端点的距离相等
设CE=x,连接AE.
∵DE是线段AB的垂直平分线.
∴AE=BE=BC+CE=3+x.
∴在Rt△ACE中,AE2=AC2+CE2.
即(3+x)2=42+x2,
考点6-3
典例精讲
垂直平分线模型
7
6
解得x=
7
6
图形示例 模型分析
在直角三角形中,当遇见斜边中点时,经常会作斜边上的中线,利用直角三角形斜边上的中线等于斜边的一半,即CD=0.5AB来证明线段间的数量关系,而且可以得到两个等腰三角形:△ACD和△BCD,该模型经常会与中位线定理一起综合应用.
B
C
A
D
考点6-4
模型分析
直角三角形的斜边中线模型
【思考】在直角三角形中遇到斜边上的中点,你想到了哪些学过的知识:___________________________________.
直角三角形斜边的中线等于斜边的一半
【例4】如图,∠ACB=90 ,点D为AB的中点,连接DC并延长到E,使CE=CD,过点B作BF∥DE,与AE的延长线交于点F,若BF=8,则AB的长度为____.
6
F
C
E
D
B
A
解:如图,∵BF∥DE,点D是AB的中点.
∴ED是△AFD的中位线.
∴BF=2ED=8.
∴ED=CE+CD=4.
∵∠ACB=90 ,D为AB的中点.
∴CD= 0.5AB.
∵CE=1/3CD.
∴AB=6.
考点6-4
典例精讲
直角三角形的斜边中线模型
图形示例 模型分析
当出现等腰三角形时,常隐含有底边中点,可利用其“三线合一”的性质.如图,在△ABC中,
(1)AC=BC;(2)CD平分∠ACB;(3)AD=BD;(4)CD⊥AB.
“知二得二”:比如由(2)(3)可得出(1)(4),也就是说,以上四条语句,任意选择两个作为条件,就可以推出剩下的两条.
A
D
C
B
考点6-5
模型分析
等腰三角形三线合一模型
【思考】在等腰三角形中遇到底边上的中点,你想到了哪些学过的知识:__________________________________________________.
【例5】如图,在△ABC中,AB=AC=5,BC=6,点M为BC的中点,MN⊥AC于点N.则MN的长为____.
A
B
N
M
C
等腰三角形底边中线、高线、顶角平分线“三线合一”
如图,连接AM.
∵AB=AC=5,点M为BC的中点.
∴AM⊥CM.
∵ 0.5AM×MC=0.5AC×MN.
考点6-5
典例精讲
等腰三角形三线合一模型
12
5
∴AM= 52-32=4
∴MN=
AM·CM
AC
12
5
=
图形示例 模型分析
当已知条件中同时出现两个及两个以上中点时,常考虑构造中位线;或出现一个中点,要证明平行线段或线段倍分关系时也常考虑构造中位线.利用三角形中位线的性质定理:DE∥BC,且DE=0.5BC,△ADE∽△ABC,则可得线段之间的相等或比例关系.
A
E
D
C
B
“角平分线,中点,垂直”只要出现了两个条件,考虑补全为等腰三角形三线合一模型.
考点6-6
模型分析
三角形中位线模型
【思考】在一般三角形中看到中点,你想到了哪些学过的知识:
_____________________________________________________________.
过中点作平行线可构造中位线,中位线平行于底边且等于底边的一半.
【例6】如图,M是△ABC的边BC的中点,AN平分∠BAC,BN⊥AN于点N,且AB=8,MN=3.则AC的长为( )A.3 B.7 C.8 D.14
D
A
N
M
C
B
D
∴AC=AD+DC=8+6=14.
解析:∵AN平分∠BAC.
∴∠BAN=∠DAN,AN=AN,∠ANB=∠AND=90 .
∴△ABN≌△AEN.
∴AD=AB=8,BN=ND.
∵M是△ABC的边BC的中点.
∴CD=2MN=2×3=6.
考点6-6
典例精讲
三角形中位线模型
知识梳理
课堂小结
中点问题常用性质及常见辅助线作法
2.一边的垂线过这边中点
垂直平分线性质;
1.中线或与中点有关线段
中线倍长构造全等;
3.圆+弦或弧的中点
垂径定理或圆周角定理.
联想
联想
联想
联想
6.多个中点或平行+中点
4.直角三角形+斜边中点
5.等腰三角形+底边中点
构造中位线;
直角三角形斜边中线性质;
等腰三角形三线合一;
联想
联想
A
N
M
D
B
C
1.如图,在四边形ABCD中,M,N分别是CD,BC的中点,且AM⊥CD,AN⊥BC.
(1)求证:∠BAD=2∠MAN;
(2)连接BD,若∠MAN=70 ,∠DBC=40 ,求∠ADC.
1
2
3
4
(1)证明:如解图,连接AC.
∵M是CD的中点,AM⊥CD.
∴AM是线段CD的垂直平分线.
∴AC=AD.
∵AM⊥CD.
∴∠3=∠4.
同理可得∠1=∠2.
(2)解:∵AM⊥CD,AN⊥BC,∠MAN=70 .
∴∠BCD=360 -90 -90 -70 =110 .
∴∠BDC=180 -∠DBC-∠BCD=30 ,∠BAD=2∠MAN=140 .
∵AB=AC,AD=AC.
∴AB=AD.
∴∠ADB=∠ABD=20 .
∴∠ADC=∠ADB+∠BDC=50 .
知识点二
针对训练
垂直平分线模型
2.如图,已知AB=24,AB⊥BC于点B,AB⊥AD于点A,AD=10,BC=20.若点E是CD的中点,则AE的长是_____.
13
A
C
B
E
D
知识点二
针对训练
垂直平分线模型
如图,在Rt△ABC中,∠ACB=90 ,CD为AB边上的高,若点A关于CD所在直线的对称点E恰好为AB的中点,则∠BCE的度数是( )
A.60 B.45 C.30 D.75
C
C
D
E
A
B
∵在Rt△ABC中,∠ACB=90 ,CD为AB边上的高,
点A关于CD所在直线的对称点E恰好为AB的中点.
∴∠CED=∠A,CE=BE=AE.
∴∠ECA=∠A,∠B=∠BCE.
∴△ACE是等边三角形.
∴∠CED=60 .
∴∠B=∠CED=30 .
∴∠A=60 .
知识点三
针对训练
直角三角形的斜边中线模型
如图,在矩形ABCD中,点E为AB边上一点,EC平分∠DEB,点F为CE的中点,连接AF,BF.过点E作EH∥BC分别交AF,CD于G,H两点.
求证:(1)DE=DC;(2)AF⊥BF.
A
M
H
D
C
B
E
F
G
证明:(1)∵四边形ABCD是矩形
∴AB∥CD.
∴∠DCE=∠CEB.
∵EC平分∠DEB.
∴∠DCE=∠CEB.
∴∠DCE=∠DEC.
∴DE=DC.
(2)连接DF.
∵DE=DC,点F为CE的中点,
∴DF⊥EC.
∴∠DFC=90 .
在矩形ABCD,AB=DC,∠ABC=90 ,
∴BF=CF=EF=0.5EC
∴∠ABF=∠CEB.
∵∠DCE=∠CEB,
∴∠ABF=∠DCF.
在△ABF和△DCF中
BF=CF
∠ABF=∠DCFAB=DC
∴△ABF≌△DCF(SAS)
∴∠AFB=∠DFC=90
∴AF⊥BF.
知识点四
针对训练
等腰三角形三线合一模型
在△ABC中,CD平分∠ACB,AD⊥CD,E是AB中点,AC=15,BC=27,求DE的长.
等腰中,造三线,两个条件快补全.
三线合一+中位线
F
【分析】本题中,点E已经是AB的中点,由CD平分∠ACB,
AD⊥CD,想到可以构造等腰三角形,利用三线合一,使点D成为另一个中点,从而让ED变成“看得见”的中位线.
∴DE=0.5BF=0.5(BC-CF)=0.5(BC-AC)=6.
解:延长AD交BC于F.
∵CD平分∠ACB,AD⊥CD
∴∠ACD=∠FCD,∠ADC=∠FDC=90 ,
∴∠CAD=∠CFD
∴AC=CF,AD=FD
∵E是AB的中点,D是FA的中点.
∴DE是△ABF的中位线,
知识点五
针对训练
三角形中位线模型
A
D
E
C
B
1.如图1,在△ABC中,AB=AC,A=30 ,AB的垂直平分线l交AC于点D,则∠CBD的度数为( ) A.30 B.45 C.50 D.75
2.如图2,在 Rt△ABC中,∠ACB=90°,点D,E分别是边AB,AC的中点,延长BC至点F,使CF=0.5BC,若AB=10,则EF的长是____.
B
A
F
E
D
B
C
图2
5
提升能力
强化训练
中点问题的常见模型
A
l
D
C
B
图1
4.如图,D是△ABC内一点,BD⊥CD,AD=12,BD=8,CD=6,点E,F,G,H分别是AB,
AC,CD,BD的中点,则四边形EFGH的周长是____.
5.如图,△ABC的面积是12,点D,E,F,G分别是BC,AD,BE,CE的中点,则△AFG的面积是____.
6.如图,在Rt△ABC中,D为斜边AC的中点,E为BD上一点,F为CE的中点.若AE=AD,DF=2,则BD的长为____.
22
4.5
A
D
G
H
F
E
C
B
A
G
F
D
C
B
E
提升能力
强化训练
中点问题的常见模型
4
A
F
E
D
C
B
7.如图,点M是△ABC的边BC的中点,AN平分∠BAC,BN⊥AN于点N,延长BN交AC于点D,已知AB=10,AC=16,则MN=____.
8.如图,在△ABC中,D是AB上一点,AD=AC,AE平分∠CAD,交CD于点E,F是BC的中点,若BD=16,则EF的长为____.
9.如图,在△ABC中,AB=8,AC=6,AD,AE分别是其角平分线和中线,点C作CG⊥AD于点F,交AB于点G,连接EF,则线段EF的长为____.
3
A
N
D
C
M
B
8
C
F
E
B
D
A
1
A
D
E
C
B
G
F
提升能力
强化训练
中点问题的常见模型
11.如图,在△ABC中,若∠B=2∠C,AD⊥BC,E为BC边中点,求证:AB=2DE.
F
EF为中位线,综合已知条件易得:DE=DF
A
E
D
C
B
提升能力
强化训练
中点问题的常见模型
【变式】如图,在△ABC中,AB=2,AC=3,E为BC的中点,AD平分∠BAC,CF⊥AD交AD的延长线于点F,求EF的长.
B
D
E
F
C
A
P
A
E
D
C
B
F
A
B
E
D
C
12.如图,在Rt△ABC中,∠ACB=90 ,CD为AB边上的高,CE为AB边上的中线,AD=4,CE=10,求CD的长.
解:在Rt△ABC中∠ACB=90 ,CE为AB边上的中线,CE=10,
∴AE=CE=10.
∵AD=4,
∴DE=6.
∵CD为AB边上的高,
∴在Rt△CDE中,
提升能力
强化训练
中点问题的常见模型
CD=
CE2-DE2
= 102-62=8.
14.如图,在平行四边形ABCD中,AC⊥BC,点E,F分别在AB,BC上,且满足AC=AE=CF,连接CE,AF,EF.
(1)若∠ABC=35°,求∠EAF的度数;
(2)若CE⊥EF,求证:CE=2EF.
A
E
B
F
C
D
M
∴CE=2EF.
(1)解:∵AC⊥BC,AC=CF.
∴△ACF为等腰直角三角形,则∠AFC=45 .
∵∠AFC=∠B+∠EAF,∠B=35 .
∴∠EAF=10 ;
(2)证明:如解图①,取CF的中点M,连接EM、AM.
∵CE⊥EF
∴EM=CM=FM=0.5CF.
∵AC=AE,
∴AM为EC的中垂线.
∴∠CAM+∠ACE=90 .
∵∠ECF+∠ACE=90 .
∴∠CAM=∠FCE.
∵∠CEF=∠ACM=90 .
∴△ACM∽△CEF.
∵CF=AC=2CM.
∴AC:CM=CE:EF=2:1
∴AC:CM=CE:EF
提升能力
强化训练
中点问题的常见模型
15.如图,在△ABC中,AD是高,CE是中线,点G是CE的中点,DG⊥CE于点G.
(1)求证:DC=BE;
(2)若∠AEC=66 ,求∠BCE的度数.
A
G
E
D
C
B
(1)证明:连接DE.
∵AD⊥BC,
∴∠ADB=90 .
∵AE=BE.
∴DE=BE=AE.
∵DG⊥EC,点G是CE的中点.
∴DE=CD.
∴DC=BE.
(2)解:设∠BCE=x.
∵BE=DE=DC,
∴∠DEC=∠DCE=x.
∴∠EBD=∠BDE=∠DEC+∠DCE=2x.
∵∠AEC=∠EBD+∠ECD,
∴66 =3x.
∴x=22 .
∴∠BCE=22 .
提升能力
强化训练
中点问题的常见模型
同课章节目录
