专题2.3(1)矩形的折叠问题 课件(共19张PPT)-中考数学二轮复习必会几何模型剖析(全国通用)
文档属性
| 名称 | 专题2.3(1)矩形的折叠问题 课件(共19张PPT)-中考数学二轮复习必会几何模型剖析(全国通用) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-25 06:48:24 | ||
图片预览






文档简介
(共19张PPT)
专题二 轴对称模型
§2.3 矩形的折叠
人教版中考第二轮总复习---几何模型
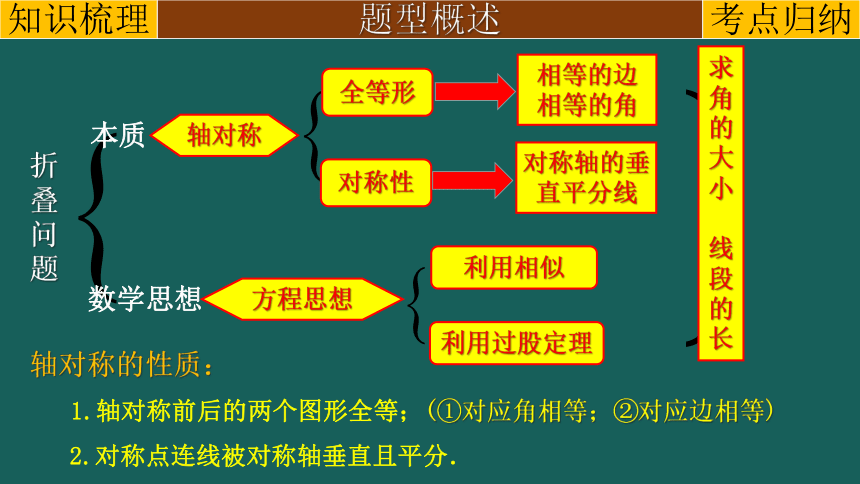
折叠问题
数学思想
本质
轴对称
方程思想
全等形
对称性
相等的边
相等的角
对称轴的垂直平分线
利用相似
利用过股定理
求角的大小
线段的长
考点归纳
知识梳理
题型概述
轴对称的性质:
1.轴对称前后的两个图形全等;(①对应角相等;②对应边相等)
2.对称点连线被对称轴垂直且平分.
考点归纳
知识梳理
矩形折叠的常见类型
A
B
C
D
C
E
A
B
C
D
D
E
A
B
C
D
A
E
A
B
C
D
A
E
△ABD 与△D CE有什么关系
(1)△ABE与△C DE有什么关系
(2)△BDE是什么三角形.
A
F
D
E
D
B
C
3
5
x
5-x
5-x
3
△A DE是什么三角形.
点A 的运动路径?
A
B
C
D
D
C
F
E
M
△MEF是什么三角形.
(1)△ABE与△C DE有什么关系
(2)△BDE是什么三角形.
【例1】如图,直线EF是矩形ABCD的对称轴,点P在CD边上,将△BCP沿BP折叠,点C恰好落在线段AP与EF的交点Q处,BC=4,则线段AB的长是___.
30
30
30
A
P
D
C
E
F
B
Q
8
4 3
4 3
【分析】根据图形位置的特殊性,寻找隐含条件.
根据点Q在EF上且∠BQP=90 .
∴∠ABQ=∠PBQ=∠CBP=30 .
∴AB=8.
∵BC=4 ,
3
8
∴BQ=
4 3
考点5-1
典例精讲
矩形的折叠与全等三角形
【例2】如图,矩形ABCD中,AB=3,BC=12,点E是AD边的中点,点F是AB上的一点,将△AEF沿EF折叠后,点A恰好落到CF上的点G处,则折痕EF=______.
A
G
E
F
C
D
B
【小结】从中点处翻折,则另外部分亦可翻折.
【分析】有特殊位置关系必然有隐藏结论.
连接CE,易证△CED≌△CEG(HL).
∴∠CEF=90 ,
易证△CDE∽△EAF,
可得:
CD
EA
=
CE
EF
由CD=3 ,ED=EA=6.
6
∴CE=3 .
10
代入比例式,得:
EF= =
3 10×6
3 6
2 15
2 15
考点5-2
典例精讲
矩形的折叠与相似三角形
13.如图,四边形ABCD是矩形纸片,将△BCD沿BD折叠,得到△BED,BE交AD于点F,AB=3,AF:FD=1:2,则AF=____.
A
F
E
D
C
B
x
3
2x
2x
x=
3
x2-32=(2x)2,
3
考点5-3
典例精讲
矩形的折叠与勾股定理
【分析】易证△AFB≌△EFD.
【小结】沿对角线折叠,则必有一组全等.
∴AF= .
3
设AF=x,则BF=DF=2x,又AB=3.
解得:x=
3
故x2-32=(2x)2,
∴BF=DF.
【例4】如图,矩形纸片ABCD,AB=4,BC=3,点P在BC边上,将△CDP沿DP折叠,点C落在点E处,PE、DE分别交AB于点O、F,且OP=OF,则cos∠ADF的值为( )
A. B. C. D.
A
F
E
D
C
P
O
B
4
4-x
x+1
【小结】对称点落在矩形外,也可能有全等,有相等线段便可用用勾股与相似.
C
【分析】根据0P=0F,易证△0EF≌△0BP,
∴0E=0B,0E+0P=0B+0F,即EP=BF.
设EP=BF=x,则AF=4-x,
∵CP=EP=x,
∴EF=BP=3-x,
∴DF=4-(3-x)=x+1.
在Rt△ADF中,DF2=AD2+AF2,
代入得:(x+1)2=3+(4-x)2
解得:x= .
12
5
∴DF= .
17
5
∴cos∠ADF= .
17
5
考点5-4
典例精讲
矩形的折叠与三角形函数
【例5】如图,矩形ABCD中,AB=4,BC=6,点P是矩形ABCD内一动点,且S△PAB=S△PCD,则PC+PD的最小值为______.
A
P
C
D
B
M
N
D
【分析】与上题类似,分析出P点轨迹.
∵S△PAB=0.5S△PCD.
∵过点P作MN∥AB分别交AD、BC于M、N两点.
则M是线段AD靠近点A的三等分点,N是线段BC靠近点B的三等分点.
作点D关于MN的对称点D ,连接CD ,与MN交点即为P点.
此时PC+PD=PC+PD =CD =
42+82
=4 5
∴PC+PD的最小值为 .
4 5
4 5
考点5-5
典例精讲
矩形的折叠与最值问题
1.如图,在矩形纸片ABCD中,AB=6,BC=10,点E在CD上,将△BCE沿BE折叠,点C恰落在边AD上的点F处,点G在AF上,将△ABG沿BG折叠,点A恰落在线段BF上的点H处,有下列结论:①∠EBG=45 ;②△DEF∽△ABG;③AG+DF=FG;
④S△ABG=1.5S△FGH.其中正确的是_______.(填序号)
①③④
B
F
G
E
D
A
C
H
6
10
6
4
x
x
8-x
2
查漏补缺
针对训练
矩形的折叠
2.如图,正方形ABCD中,AB=8,AC与BD交于点O,N是AO的中点,点M在BC边上,且BM=6,P为对角线BD上一点,则PM-PN的最大值为____.
A
B
P
M
D
C
N
O
M
A
B
P
M
D
C
N
O
M
∴PM-PN的最大值为2.
【分析】求两线段差值最大的思路是“三角形两边之差小于第三边,当三点共线时差最大”,
本题的难点在于无论P在对角线BD的任何位置,都无法构造出PM-PN=MN.
作点M关于BD的对称点M ,
根据正方形的对称性可得点M 在边AB上且AM =CM=2,
∴PM-PN=PM -PN≤M N,当M 、N、P共线时取到等号.
∵N是OA中点,
∴M N=AM =2,
2
查漏补缺
针对训练
矩形的折叠
知识梳理
课堂小结
矩形的折叠
1.如图,已知矩形纸片ABCD,点E是AB的中点,点G是BC上的一点,∠BEG>60 .现沿直线EG将纸片折叠,使点B落在纸片上的点H处,连接AH,则与∠BEG相等的角的个数为____.
2.如图,把一个长方形纸片沿EF折叠后,点D、C分别落在D 、C 的位置,若∠EFB=65 ,则∠AED =____ .
3
A
H
C
D
G
B
E
A
D
C
D
E
F
C
G
B
50
65
65
65
50
提升能力
强化训练
矩形折叠
3.如图,在坐标系中,把矩形OABC的顶点O放在原点处,把边OA,OC分别放在x轴、y轴的正半轴上,点D在OC边上,把△BDC沿直线BD翻折,点C的对应点恰好落在x轴上的点E处,已知B(10,8),则直线BD的解析式为________.
4.如图,四边形ABCD是矩形,AB:AD=4:3,把矩形沿直线AC折叠,点B落在点E处,连接DE,则DE:AC=( )A.1:3 B.3:8 C.8:27 D.7:25
y
x
C
B
A
O
D
E
y= x+3
1
2
提升能力
强化训练
矩形折叠
F
H
A
D
E
C
B
4x
3x
3x
3x
2.4x
1.8x
1.8x
1.4x
1.4x
D
5.如图,矩形ABCD中,AB=1,E、F分别为AD、CD的中点,沿BE将△ABE折叠,若点A恰好落在BF上,则AD=____.
6.如图,正方形ABCD中,AB=6,G是BC的中点.将△ABG沿AG对折至△AFG,延长GF交DC于点E,则DE的长是( )
A.1 B.1.5 C.2 D.2.5
1
1
A
A
F
E
D
C
B
2
1
2
1
2
1
2
提升能力
强化训练
矩形折叠
A
G
C
E
D
B
F
6
3
3
3
x
6-x
x
C
7.如图,矩形纸片ABCD,AB=4,AD=3,折叠纸片使AD边与对角线BD重合,折痕为DG,则AG=_____.
8.如图,折叠矩形ABCD的一边AD,使点D落在BC边的点F出,已知折痕AE=5cm,且,那么矩形ABCD的周长为____cm.
1.5
A
G
A
B
C
D
3
4
3
2
x
x
4-x
x2-22=(4-x)2
x=1.5
A
E
F
D
C
B
3x
4x
5x
5x
8x
6x
10x
5 5
(3x)2-52=(4x)2
x=1
36
提升能力
强化训练
矩形折叠
9.如图,在矩形ABCD中,AB=3,AD=5,点E在DC上,将矩形ABCD沿AE折叠,点D恰好落在BC边上的点F处,那么sin∠EFC的值为___.
10.如图,在矩形ABCD中,AB=3,BC=2,H是AB的中点,将△CBH沿CH折叠,点B落在矩形内点P处,连接AP,则tan∠HAP=____.
B
D
E
F
C
A
3
5
5
4
4
5
G
A
H
P
D
C
B
4
3
3
2
2
1.5
1.5
提升能力
强化训练
矩形折叠
11.将一张宽为3的矩形纸片折叠成如图所示的图形,若AB=5,则BC=_____.
12.如图,将矩形ABCD(纸片)折叠,使点B与AD边上的点K重合,EG为折痕,点C与AD边上的点K重合,FH为折痕.已知∠1=67.5 ,∠2=75 ,EF=+1,BC=__.
A
B
C
H
5
3
4
1
10
10
提升能力
强化训练
矩形折叠
P
A
F
E
D
C
B
G
H
K
【分析】根据对称的性质.
∵∠1=67.5 ,
∴∠KEG=67.5 ,∠KEF=45 .
∵∠2=75 ,
∴∠KFH=75 ,∠KFE=30 ,
过点K作KP⊥BC交BC于P点,
设KP=x,则EP=x.
FP= x,
3
∴x+ x= +1.
3
3
解得x=1.
∴BE=KE=
2
CF=KF=2,
∴BC=BE+EF+FC= + +3
2
3
13.如图,在矩形ABCD中,AB=5,BC=6,点M,N分别在AD,BC上,AM=AD,BN=BC,
E为直线BC上一动点,连接DE,将△DCE沿DE所在的直线翻折得到△DC E,当点C 恰好落在直线MN上时,CE的长为________.
A
C
E
N
M
D
C
B
综上所述,CE的长为2.5或10.
【分析】可能情况如下:
情况一:如图2,
由题意可得:DC =DC=5,DM=4,
∴MC =3,C N=2.
对于△ENC ,设CE=x,
则C E=x,EN=4-x.
由勾股定理可得:
A
N
M
D
C
B
C
E
图2
A
B
N
M
E
C
D
C
α
F
α
α
图3
(4-x)2+22=x2,
解得:x=2.5,
CE=2.5.
情况二:如图3,
易证C F=CD=5,
∴NF=3,MF=2.
易证EN=4×1.5=6.
∴CE=10.
2.5或10
提升能力
强化训练
矩形折叠
14.如图,在矩形ABCD中,AB=2,AD=2,点E是CD的中点,连接AE,将△ADE沿直线AE折叠,使点D落在点F处,则线段CF的长度是( )
A.1 B. C. D.
M
A
F
D
E
C
B
【分析】可以考虑构造包含CF的直角三角形.
∴DF⊥AE,M是DF中点,
连接DF交AE于点M,
∵点E是DC中点,
∴ME是FC边中位线,
∴DF⊥FC,
由AD·DE=AE·DM,得:DM=
2 3
3
∴DF=
4 2
3
勾股定理得:CF= =
22-( )2
4 2
3
2
3
B
提升能力
强化训练
矩形折叠
专题二 轴对称模型
§2.3 矩形的折叠
人教版中考第二轮总复习---几何模型
折叠问题
数学思想
本质
轴对称
方程思想
全等形
对称性
相等的边
相等的角
对称轴的垂直平分线
利用相似
利用过股定理
求角的大小
线段的长
考点归纳
知识梳理
题型概述
轴对称的性质:
1.轴对称前后的两个图形全等;(①对应角相等;②对应边相等)
2.对称点连线被对称轴垂直且平分.
考点归纳
知识梳理
矩形折叠的常见类型
A
B
C
D
C
E
A
B
C
D
D
E
A
B
C
D
A
E
A
B
C
D
A
E
△ABD 与△D CE有什么关系
(1)△ABE与△C DE有什么关系
(2)△BDE是什么三角形.
A
F
D
E
D
B
C
3
5
x
5-x
5-x
3
△A DE是什么三角形.
点A 的运动路径?
A
B
C
D
D
C
F
E
M
△MEF是什么三角形.
(1)△ABE与△C DE有什么关系
(2)△BDE是什么三角形.
【例1】如图,直线EF是矩形ABCD的对称轴,点P在CD边上,将△BCP沿BP折叠,点C恰好落在线段AP与EF的交点Q处,BC=4,则线段AB的长是___.
30
30
30
A
P
D
C
E
F
B
Q
8
4 3
4 3
【分析】根据图形位置的特殊性,寻找隐含条件.
根据点Q在EF上且∠BQP=90 .
∴∠ABQ=∠PBQ=∠CBP=30 .
∴AB=8.
∵BC=4 ,
3
8
∴BQ=
4 3
考点5-1
典例精讲
矩形的折叠与全等三角形
【例2】如图,矩形ABCD中,AB=3,BC=12,点E是AD边的中点,点F是AB上的一点,将△AEF沿EF折叠后,点A恰好落到CF上的点G处,则折痕EF=______.
A
G
E
F
C
D
B
【小结】从中点处翻折,则另外部分亦可翻折.
【分析】有特殊位置关系必然有隐藏结论.
连接CE,易证△CED≌△CEG(HL).
∴∠CEF=90 ,
易证△CDE∽△EAF,
可得:
CD
EA
=
CE
EF
由CD=3 ,ED=EA=6.
6
∴CE=3 .
10
代入比例式,得:
EF= =
3 10×6
3 6
2 15
2 15
考点5-2
典例精讲
矩形的折叠与相似三角形
13.如图,四边形ABCD是矩形纸片,将△BCD沿BD折叠,得到△BED,BE交AD于点F,AB=3,AF:FD=1:2,则AF=____.
A
F
E
D
C
B
x
3
2x
2x
x=
3
x2-32=(2x)2,
3
考点5-3
典例精讲
矩形的折叠与勾股定理
【分析】易证△AFB≌△EFD.
【小结】沿对角线折叠,则必有一组全等.
∴AF= .
3
设AF=x,则BF=DF=2x,又AB=3.
解得:x=
3
故x2-32=(2x)2,
∴BF=DF.
【例4】如图,矩形纸片ABCD,AB=4,BC=3,点P在BC边上,将△CDP沿DP折叠,点C落在点E处,PE、DE分别交AB于点O、F,且OP=OF,则cos∠ADF的值为( )
A. B. C. D.
A
F
E
D
C
P
O
B
4
4-x
x+1
【小结】对称点落在矩形外,也可能有全等,有相等线段便可用用勾股与相似.
C
【分析】根据0P=0F,易证△0EF≌△0BP,
∴0E=0B,0E+0P=0B+0F,即EP=BF.
设EP=BF=x,则AF=4-x,
∵CP=EP=x,
∴EF=BP=3-x,
∴DF=4-(3-x)=x+1.
在Rt△ADF中,DF2=AD2+AF2,
代入得:(x+1)2=3+(4-x)2
解得:x= .
12
5
∴DF= .
17
5
∴cos∠ADF= .
17
5
考点5-4
典例精讲
矩形的折叠与三角形函数
【例5】如图,矩形ABCD中,AB=4,BC=6,点P是矩形ABCD内一动点,且S△PAB=S△PCD,则PC+PD的最小值为______.
A
P
C
D
B
M
N
D
【分析】与上题类似,分析出P点轨迹.
∵S△PAB=0.5S△PCD.
∵过点P作MN∥AB分别交AD、BC于M、N两点.
则M是线段AD靠近点A的三等分点,N是线段BC靠近点B的三等分点.
作点D关于MN的对称点D ,连接CD ,与MN交点即为P点.
此时PC+PD=PC+PD =CD =
42+82
=4 5
∴PC+PD的最小值为 .
4 5
4 5
考点5-5
典例精讲
矩形的折叠与最值问题
1.如图,在矩形纸片ABCD中,AB=6,BC=10,点E在CD上,将△BCE沿BE折叠,点C恰落在边AD上的点F处,点G在AF上,将△ABG沿BG折叠,点A恰落在线段BF上的点H处,有下列结论:①∠EBG=45 ;②△DEF∽△ABG;③AG+DF=FG;
④S△ABG=1.5S△FGH.其中正确的是_______.(填序号)
①③④
B
F
G
E
D
A
C
H
6
10
6
4
x
x
8-x
2
查漏补缺
针对训练
矩形的折叠
2.如图,正方形ABCD中,AB=8,AC与BD交于点O,N是AO的中点,点M在BC边上,且BM=6,P为对角线BD上一点,则PM-PN的最大值为____.
A
B
P
M
D
C
N
O
M
A
B
P
M
D
C
N
O
M
∴PM-PN的最大值为2.
【分析】求两线段差值最大的思路是“三角形两边之差小于第三边,当三点共线时差最大”,
本题的难点在于无论P在对角线BD的任何位置,都无法构造出PM-PN=MN.
作点M关于BD的对称点M ,
根据正方形的对称性可得点M 在边AB上且AM =CM=2,
∴PM-PN=PM -PN≤M N,当M 、N、P共线时取到等号.
∵N是OA中点,
∴M N=AM =2,
2
查漏补缺
针对训练
矩形的折叠
知识梳理
课堂小结
矩形的折叠
1.如图,已知矩形纸片ABCD,点E是AB的中点,点G是BC上的一点,∠BEG>60 .现沿直线EG将纸片折叠,使点B落在纸片上的点H处,连接AH,则与∠BEG相等的角的个数为____.
2.如图,把一个长方形纸片沿EF折叠后,点D、C分别落在D 、C 的位置,若∠EFB=65 ,则∠AED =____ .
3
A
H
C
D
G
B
E
A
D
C
D
E
F
C
G
B
50
65
65
65
50
提升能力
强化训练
矩形折叠
3.如图,在坐标系中,把矩形OABC的顶点O放在原点处,把边OA,OC分别放在x轴、y轴的正半轴上,点D在OC边上,把△BDC沿直线BD翻折,点C的对应点恰好落在x轴上的点E处,已知B(10,8),则直线BD的解析式为________.
4.如图,四边形ABCD是矩形,AB:AD=4:3,把矩形沿直线AC折叠,点B落在点E处,连接DE,则DE:AC=( )A.1:3 B.3:8 C.8:27 D.7:25
y
x
C
B
A
O
D
E
y= x+3
1
2
提升能力
强化训练
矩形折叠
F
H
A
D
E
C
B
4x
3x
3x
3x
2.4x
1.8x
1.8x
1.4x
1.4x
D
5.如图,矩形ABCD中,AB=1,E、F分别为AD、CD的中点,沿BE将△ABE折叠,若点A恰好落在BF上,则AD=____.
6.如图,正方形ABCD中,AB=6,G是BC的中点.将△ABG沿AG对折至△AFG,延长GF交DC于点E,则DE的长是( )
A.1 B.1.5 C.2 D.2.5
1
1
A
A
F
E
D
C
B
2
1
2
1
2
1
2
提升能力
强化训练
矩形折叠
A
G
C
E
D
B
F
6
3
3
3
x
6-x
x
C
7.如图,矩形纸片ABCD,AB=4,AD=3,折叠纸片使AD边与对角线BD重合,折痕为DG,则AG=_____.
8.如图,折叠矩形ABCD的一边AD,使点D落在BC边的点F出,已知折痕AE=5cm,且,那么矩形ABCD的周长为____cm.
1.5
A
G
A
B
C
D
3
4
3
2
x
x
4-x
x2-22=(4-x)2
x=1.5
A
E
F
D
C
B
3x
4x
5x
5x
8x
6x
10x
5 5
(3x)2-52=(4x)2
x=1
36
提升能力
强化训练
矩形折叠
9.如图,在矩形ABCD中,AB=3,AD=5,点E在DC上,将矩形ABCD沿AE折叠,点D恰好落在BC边上的点F处,那么sin∠EFC的值为___.
10.如图,在矩形ABCD中,AB=3,BC=2,H是AB的中点,将△CBH沿CH折叠,点B落在矩形内点P处,连接AP,则tan∠HAP=____.
B
D
E
F
C
A
3
5
5
4
4
5
G
A
H
P
D
C
B
4
3
3
2
2
1.5
1.5
提升能力
强化训练
矩形折叠
11.将一张宽为3的矩形纸片折叠成如图所示的图形,若AB=5,则BC=_____.
12.如图,将矩形ABCD(纸片)折叠,使点B与AD边上的点K重合,EG为折痕,点C与AD边上的点K重合,FH为折痕.已知∠1=67.5 ,∠2=75 ,EF=+1,BC=__.
A
B
C
H
5
3
4
1
10
10
提升能力
强化训练
矩形折叠
P
A
F
E
D
C
B
G
H
K
【分析】根据对称的性质.
∵∠1=67.5 ,
∴∠KEG=67.5 ,∠KEF=45 .
∵∠2=75 ,
∴∠KFH=75 ,∠KFE=30 ,
过点K作KP⊥BC交BC于P点,
设KP=x,则EP=x.
FP= x,
3
∴x+ x= +1.
3
3
解得x=1.
∴BE=KE=
2
CF=KF=2,
∴BC=BE+EF+FC= + +3
2
3
13.如图,在矩形ABCD中,AB=5,BC=6,点M,N分别在AD,BC上,AM=AD,BN=BC,
E为直线BC上一动点,连接DE,将△DCE沿DE所在的直线翻折得到△DC E,当点C 恰好落在直线MN上时,CE的长为________.
A
C
E
N
M
D
C
B
综上所述,CE的长为2.5或10.
【分析】可能情况如下:
情况一:如图2,
由题意可得:DC =DC=5,DM=4,
∴MC =3,C N=2.
对于△ENC ,设CE=x,
则C E=x,EN=4-x.
由勾股定理可得:
A
N
M
D
C
B
C
E
图2
A
B
N
M
E
C
D
C
α
F
α
α
图3
(4-x)2+22=x2,
解得:x=2.5,
CE=2.5.
情况二:如图3,
易证C F=CD=5,
∴NF=3,MF=2.
易证EN=4×1.5=6.
∴CE=10.
2.5或10
提升能力
强化训练
矩形折叠
14.如图,在矩形ABCD中,AB=2,AD=2,点E是CD的中点,连接AE,将△ADE沿直线AE折叠,使点D落在点F处,则线段CF的长度是( )
A.1 B. C. D.
M
A
F
D
E
C
B
【分析】可以考虑构造包含CF的直角三角形.
∴DF⊥AE,M是DF中点,
连接DF交AE于点M,
∵点E是DC中点,
∴ME是FC边中位线,
∴DF⊥FC,
由AD·DE=AE·DM,得:DM=
2 3
3
∴DF=
4 2
3
勾股定理得:CF= =
22-( )2
4 2
3
2
3
B
提升能力
强化训练
矩形折叠
同课章节目录
