专题2.3(2)矩形的折叠问题-中考数学二轮复习必会几何模型剖析(全国通用)
文档属性
| 名称 | 专题2.3(2)矩形的折叠问题-中考数学二轮复习必会几何模型剖析(全国通用) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-25 09:34:31 | ||
图片预览





文档简介
(共18张PPT)
专题二 轴对称模型
§2.3 矩形的折叠
人教版中考第二轮总复习---几何模型
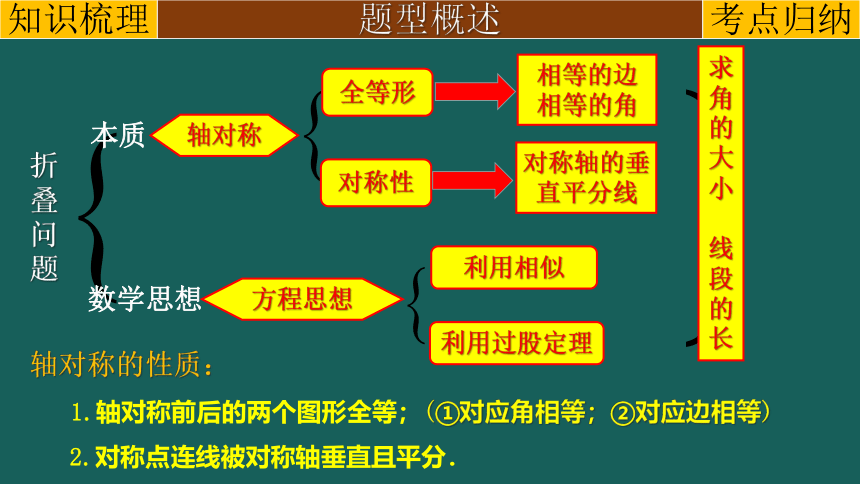
折叠问题
数学思想
本质
轴对称
方程思想
全等形
对称性
相等的边
相等的角
对称轴的垂直平分线
利用相似
利用过股定理
求角的大小
线段的长
考点归纳
知识梳理
题型概述
轴对称的性质:
1.轴对称前后的两个图形全等;(①对应角相等;②对应边相等)
2.对称点连线被对称轴垂直且平分.
考点归纳
知识梳理
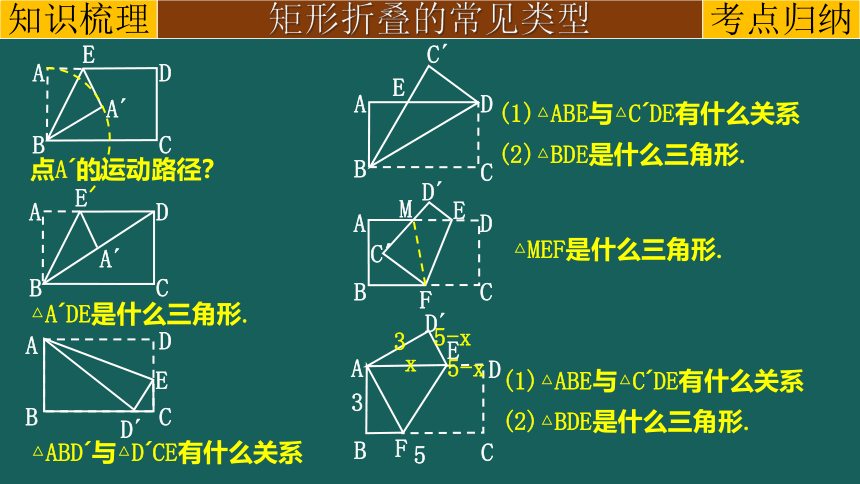
矩形折叠的常见类型
A
B
C
D
C
E
A
B
C
D
D
E
A
B
C
D
A
E
A
B
C
D
A
E
△ABD 与△D CE有什么关系
(1)△ABE与△C DE有什么关系
(2)△BDE是什么三角形.
A
F
D
E
D
B
C
3
5
x
5-x
5-x
3
△A DE是什么三角形.
点A 的运动路径?
A
B
C
D
D
C
F
E
M
△MEF是什么三角形.
(1)△ABE与△C DE有什么关系
(2)△BDE是什么三角形.
考点5-1
典例精讲
矩形的折叠与全等三角形
对称的图形中可能会有特殊角,而此时特殊角带来的不仅仅是其本身,也可能会连带其他角也变成特殊角.
【例1】如图,在矩形ABCD中,AD=3,M是CD上一点,将△ADM沿直线AM对折得到△ANM,若AN平分∠MAB,则折痕AM的长为( )
A.3 B.2 C.3 D.6
B
30
30
30
【分析】找出图中隐藏的特殊角.由题意可得:
∠DAM=∠MAN=∠NAB=30
∵AD=3,
∴DM= ,AM=
3
2 3.
A
N
M
D
C
B
考点5-2
典例精讲
矩形的折叠与相似三角形
【例2】如图,将面积为32的矩形ABCD沿对角线BD折叠,点A的对应点为点P,连接AP交BC于点E.若BE=,则AP的长为______.
A
E
C
P
D
B
【分析】由对称可得AP⊥BD,易证△ABE∽△DAB,
设AB=x,则:
BE
AB
=
AB
DA
代入得: =
2
x
x
DA
∴DA= x2.
2
2
∵矩形ABCD面积为32 .
2
∴x· x2=32 .
2
2
2
解得:x=4.
∴AB=4,AD=8 ,
2
128+16=
BD= =12,
144
记AP与BD交点为H,则AB·AD=AH·BD,
代入解得:AH=
8 2
3
∴AP=
16 2
3
性质2:对称点连线被对称轴垂直且平分,连接对称点连线可得垂直,由垂直,可得直角三角形,可得三垂直全等或相似,由三角函数,但终可求线段长.
16 2
3
H
考点5-3
典例精讲
矩形的折叠与勾股定理
【例3】如图,折叠长方形的一边AD,点D落在BC边的点F处,已知AB=8cm,AD=10cm,则EC=___.
A
E
F
D
C
B
8
10
x
8-x
10
8-x
6
4
42+x2=(8-x)2
x=3
3
方法一:利用勾股定理
方法二:利用相似
x:6=4:8
x=3
考点5-4
典例精讲
矩形的折叠与三角形函数
【例4】如图,在矩形ABCD中,AB=4,BC=,E为CD边上一点,将△BCE沿BE折叠,使得C落到矩形内点F的位置,连接AF,若tan∠BAF=,则CE=______.
A
F
E
D
C
B
M
N
x
2x
4-2x
【分析】过F点作MN∥BC分别交AB、CD于M、N两点.
∴tan∠BAF=
1
2
设FM=x,则AM=2x,BM=4-2x.
在Rt△BMF中:x2+(4-2x)2=( )2,
5
解得:x1=1,x2= (舍),
11
5
易证△BMF∽△FNE.
BF
EF
=
BM
FN
∴
【小结】对称点落在内部则可作辅助线,使点落在矩形边上.
代入得:
EF
=
2
5
5-1
解得:EF=
5- 5
2
∴CE的长为
5- 5
2
5- 5
2
【例5】如图,在矩形ABCD中,AB=6,AD=3,动点P满足S△PAB=S矩形ABCD,则点P到A、B两点距离之和PA+PB的最小值为( )
A.2 B.2 C.3 D.
A
P
D
C
B
A
M
N
作点A关于直线MN的对称点A ,连接A B,与MN交点即为点P.
A
【分析】将军饮马问题的基本思路是“作关于动点所在直线的对称,化折线为直线”,本题的一个难点在于要分析出动点P的轨迹是一条直线.
根据S△PAB= S矩形ABCD.
1
3
42+62
=2 13
过点P作MN∥AB分别交AD、BC于M、N两点,则M是线段AD靠近点D的三等分点,N是线段BC靠近点C的三等分点.
此时PA+PB=PA +PB=A B=
考点5-5
典例精讲
矩形的折叠与最值问题
如图,在正方形ABCD中,E是BC边上的一点,BE=4,EC=8,将正方形AB沿AE折叠到AF,延长EF交DC于G,连接AG,FC,现在有如下4个结论:①∠EAG=45 ;②FG=FC;③FC∥AG;④S△GFC=14.其中正确结论是_____.
A
D
C
B
F
G
E
查漏补缺
针对训练
矩形的折叠
4
8
4
x
x
12-x
82+(12-x)2=(4+x)2
x=6
①③
知识梳理
课堂小结
矩形的折叠
1.如图,在一张矩形纸片ABCD中,AD=4cm,点E,F分别是CD和AB的中点,现将这张纸片折叠,使点B落在EF上的点G处,折痕为AH,若HG延长线恰好经过点D,则CD的长为_____.
2.如图,边长为的正方形ABCD的对角线AC与BD交于点O,将正方形ABCD沿直线DF折叠,点C落在对角线BD上的点E处,折痕DF交AC于点M.则OM=_____.
A
F
G
E
H
D
C
B
4
4
2 3
提升能力
强化训练
矩形折叠
2-1
A
F
M
E
O
B
C
D
2
2-1
1
2-1
3.如图,将矩形ABCD的四个角向内翻折后,恰好拼成一个无缝隙无重叠的四边形EFGH,EH=12cm,EF=16cm,则边AD的长是____cm.
4.矩形ABCD按如图的方式折叠,BE,EG,FG为折痕,若顶点A,C,D都落在点O处,且点B,O,G在同一条直线上,同时点E,O,F在另一条直线上,则=___.
20
A
H
E
C
D
B
F
G
12
16
20
B
E
A
D
C
F
O
G
b
b
2
b
2
a
2
a
2
2
a
相似
提升能力
强化训练
矩形折叠
5.如图,矩形AOBC边OB,OA分别在x轴,y轴上,点A坐标为(0,3),∠OAB=60 ,以AB为对称轴对折后,使C点落在D点处,则D点坐标为__________.
6.如图,在矩形ABCD中,AB=6,BC=10,将矩形ABCD沿BE折叠,点A落在A 处,若EA 处,若EA 的延长线恰好过点C,则sin∠ABE的值为_____.
y
x
A
B
D
C
O
3
H
AH=4.5
OH=AH-AO=4.5-3=1.5
( ,- )
3 3
2
3
2
( ,- )
3 3
2
3
2
3 3
3 3
3 3
3 3
2
提升能力
强化训练
矩形折叠
A
B
A
E
D
C
2 10
6
10
6
8
6
8
2
10
10
7.如图,在矩形ABCD中,AB=2,BC=3,点E为AD上一点,且∠ABE=30 ,将△ABE沿BE翻折,得到△A BE,连接CA 并延长交AD于点F,则DF的长为______.
H
B
A
E
F
A
D
C
∵tan∠DFC=
【小结】矩形对称,自带直角也要再构造直角,勾股、相似、三角函数均与直角相关,明确了思路解题便不是难事.
【分析】可通过三角函数值来计算.
由题意得:∠ABE=∠A BE=∠A BC=30 ,
过点A 作A H⊥BC交BC于H点,
则A H=1,BH= ,
3
3
∴CH=3- ,tan∠FCB=
1
3- 3
3+ 3
6
=
12
3+ 3
=2(3- 3)
=6-2 3.
6-2 3
提升能力
强化训练
矩形折叠
8.如图,在矩形ABCD中,AD=2.将∠A向内翻折,点A落在BC上,记为A ,折痕为DE.若将∠B沿EA 向内翻折,点B恰好落在DE上,记为B ,则AB=____.
A
B
D
C
B
E
A
2
60
60
60
1
1
3
3
30
30
60
60
3
提升能力
强化训练
矩形折叠
9.把一张宽为1cm的长方形纸片ABCD折叠成如图中阴影部分所示的形状,顶点A,D的对应点A ,D 互相重合,中间空白部分是以E为直角顶点,腰长为2cm的等腰直角三角形,则纸片的长AD(单位cm)为( )
A.7+3 B.7+4 C.8+3 D.8+4
A
A (D )
B
C
D
E
2
2
1
1
1
2
2
2 2
1
1
D
直角三角形
提升能力
强化训练
矩形折叠
10.如图,把某矩形纸片ABCD沿EF,GH折叠,使点B和点C落在AD边上同一点P处,点A的对称点为点A ,点D的对称点为点D ,若∠FPG=90 ,△A EP的面积为4,△D PH的面积为1,则矩形ABCD的面积等于______.
A
P
G
F
D
A
H
E
D
C
B
【分析】求矩形面积,考虑能否把矩形相邻两边都算出来.两端往中间折叠,则可得:A P=D P.
∵∠FPG=90 ,
∴A PD =90 ,
易证△A EP∽△D PH.
考虑两三角形面积分别是4和1,
∴相似比为2:1.
设AB=a,则A P=D P=a,D H=0.5a,A E=2a,
EP= a,PH= a
5
5
2
表示△D PH面积: · ·a=1,
1
2
a
2
解得a=2.
AD=2a+ a+ a+ =5+3 ,
5
5
2
a
2
5
∵AB=2.
∴矩形ABCD面积为2×(5+3 )=10+6 .
5
5
提升能力
强化训练
矩形折叠
11.如图,正方形纸片ABCD的边长为12,E是边CD上一点,连接AE、折叠该纸片,使点A落在AE上的G点,并使折痕经过点B,得到折痕BF,点F在AD上,若DE=5,则GE的长为____.
A
G
F
E
D
C
B
12
5
5
5
60
13
49
13
等积
提升能力
强化训练
矩形折叠
专题二 轴对称模型
§2.3 矩形的折叠
人教版中考第二轮总复习---几何模型
折叠问题
数学思想
本质
轴对称
方程思想
全等形
对称性
相等的边
相等的角
对称轴的垂直平分线
利用相似
利用过股定理
求角的大小
线段的长
考点归纳
知识梳理
题型概述
轴对称的性质:
1.轴对称前后的两个图形全等;(①对应角相等;②对应边相等)
2.对称点连线被对称轴垂直且平分.
考点归纳
知识梳理
矩形折叠的常见类型
A
B
C
D
C
E
A
B
C
D
D
E
A
B
C
D
A
E
A
B
C
D
A
E
△ABD 与△D CE有什么关系
(1)△ABE与△C DE有什么关系
(2)△BDE是什么三角形.
A
F
D
E
D
B
C
3
5
x
5-x
5-x
3
△A DE是什么三角形.
点A 的运动路径?
A
B
C
D
D
C
F
E
M
△MEF是什么三角形.
(1)△ABE与△C DE有什么关系
(2)△BDE是什么三角形.
考点5-1
典例精讲
矩形的折叠与全等三角形
对称的图形中可能会有特殊角,而此时特殊角带来的不仅仅是其本身,也可能会连带其他角也变成特殊角.
【例1】如图,在矩形ABCD中,AD=3,M是CD上一点,将△ADM沿直线AM对折得到△ANM,若AN平分∠MAB,则折痕AM的长为( )
A.3 B.2 C.3 D.6
B
30
30
30
【分析】找出图中隐藏的特殊角.由题意可得:
∠DAM=∠MAN=∠NAB=30
∵AD=3,
∴DM= ,AM=
3
2 3.
A
N
M
D
C
B
考点5-2
典例精讲
矩形的折叠与相似三角形
【例2】如图,将面积为32的矩形ABCD沿对角线BD折叠,点A的对应点为点P,连接AP交BC于点E.若BE=,则AP的长为______.
A
E
C
P
D
B
【分析】由对称可得AP⊥BD,易证△ABE∽△DAB,
设AB=x,则:
BE
AB
=
AB
DA
代入得: =
2
x
x
DA
∴DA= x2.
2
2
∵矩形ABCD面积为32 .
2
∴x· x2=32 .
2
2
2
解得:x=4.
∴AB=4,AD=8 ,
2
128+16=
BD= =12,
144
记AP与BD交点为H,则AB·AD=AH·BD,
代入解得:AH=
8 2
3
∴AP=
16 2
3
性质2:对称点连线被对称轴垂直且平分,连接对称点连线可得垂直,由垂直,可得直角三角形,可得三垂直全等或相似,由三角函数,但终可求线段长.
16 2
3
H
考点5-3
典例精讲
矩形的折叠与勾股定理
【例3】如图,折叠长方形的一边AD,点D落在BC边的点F处,已知AB=8cm,AD=10cm,则EC=___.
A
E
F
D
C
B
8
10
x
8-x
10
8-x
6
4
42+x2=(8-x)2
x=3
3
方法一:利用勾股定理
方法二:利用相似
x:6=4:8
x=3
考点5-4
典例精讲
矩形的折叠与三角形函数
【例4】如图,在矩形ABCD中,AB=4,BC=,E为CD边上一点,将△BCE沿BE折叠,使得C落到矩形内点F的位置,连接AF,若tan∠BAF=,则CE=______.
A
F
E
D
C
B
M
N
x
2x
4-2x
【分析】过F点作MN∥BC分别交AB、CD于M、N两点.
∴tan∠BAF=
1
2
设FM=x,则AM=2x,BM=4-2x.
在Rt△BMF中:x2+(4-2x)2=( )2,
5
解得:x1=1,x2= (舍),
11
5
易证△BMF∽△FNE.
BF
EF
=
BM
FN
∴
【小结】对称点落在内部则可作辅助线,使点落在矩形边上.
代入得:
EF
=
2
5
5-1
解得:EF=
5- 5
2
∴CE的长为
5- 5
2
5- 5
2
【例5】如图,在矩形ABCD中,AB=6,AD=3,动点P满足S△PAB=S矩形ABCD,则点P到A、B两点距离之和PA+PB的最小值为( )
A.2 B.2 C.3 D.
A
P
D
C
B
A
M
N
作点A关于直线MN的对称点A ,连接A B,与MN交点即为点P.
A
【分析】将军饮马问题的基本思路是“作关于动点所在直线的对称,化折线为直线”,本题的一个难点在于要分析出动点P的轨迹是一条直线.
根据S△PAB= S矩形ABCD.
1
3
42+62
=2 13
过点P作MN∥AB分别交AD、BC于M、N两点,则M是线段AD靠近点D的三等分点,N是线段BC靠近点C的三等分点.
此时PA+PB=PA +PB=A B=
考点5-5
典例精讲
矩形的折叠与最值问题
如图,在正方形ABCD中,E是BC边上的一点,BE=4,EC=8,将正方形AB沿AE折叠到AF,延长EF交DC于G,连接AG,FC,现在有如下4个结论:①∠EAG=45 ;②FG=FC;③FC∥AG;④S△GFC=14.其中正确结论是_____.
A
D
C
B
F
G
E
查漏补缺
针对训练
矩形的折叠
4
8
4
x
x
12-x
82+(12-x)2=(4+x)2
x=6
①③
知识梳理
课堂小结
矩形的折叠
1.如图,在一张矩形纸片ABCD中,AD=4cm,点E,F分别是CD和AB的中点,现将这张纸片折叠,使点B落在EF上的点G处,折痕为AH,若HG延长线恰好经过点D,则CD的长为_____.
2.如图,边长为的正方形ABCD的对角线AC与BD交于点O,将正方形ABCD沿直线DF折叠,点C落在对角线BD上的点E处,折痕DF交AC于点M.则OM=_____.
A
F
G
E
H
D
C
B
4
4
2 3
提升能力
强化训练
矩形折叠
2-1
A
F
M
E
O
B
C
D
2
2-1
1
2-1
3.如图,将矩形ABCD的四个角向内翻折后,恰好拼成一个无缝隙无重叠的四边形EFGH,EH=12cm,EF=16cm,则边AD的长是____cm.
4.矩形ABCD按如图的方式折叠,BE,EG,FG为折痕,若顶点A,C,D都落在点O处,且点B,O,G在同一条直线上,同时点E,O,F在另一条直线上,则=___.
20
A
H
E
C
D
B
F
G
12
16
20
B
E
A
D
C
F
O
G
b
b
2
b
2
a
2
a
2
2
a
相似
提升能力
强化训练
矩形折叠
5.如图,矩形AOBC边OB,OA分别在x轴,y轴上,点A坐标为(0,3),∠OAB=60 ,以AB为对称轴对折后,使C点落在D点处,则D点坐标为__________.
6.如图,在矩形ABCD中,AB=6,BC=10,将矩形ABCD沿BE折叠,点A落在A 处,若EA 处,若EA 的延长线恰好过点C,则sin∠ABE的值为_____.
y
x
A
B
D
C
O
3
H
AH=4.5
OH=AH-AO=4.5-3=1.5
( ,- )
3 3
2
3
2
( ,- )
3 3
2
3
2
3 3
3 3
3 3
3 3
2
提升能力
强化训练
矩形折叠
A
B
A
E
D
C
2 10
6
10
6
8
6
8
2
10
10
7.如图,在矩形ABCD中,AB=2,BC=3,点E为AD上一点,且∠ABE=30 ,将△ABE沿BE翻折,得到△A BE,连接CA 并延长交AD于点F,则DF的长为______.
H
B
A
E
F
A
D
C
∵tan∠DFC=
【小结】矩形对称,自带直角也要再构造直角,勾股、相似、三角函数均与直角相关,明确了思路解题便不是难事.
【分析】可通过三角函数值来计算.
由题意得:∠ABE=∠A BE=∠A BC=30 ,
过点A 作A H⊥BC交BC于H点,
则A H=1,BH= ,
3
3
∴CH=3- ,tan∠FCB=
1
3- 3
3+ 3
6
=
12
3+ 3
=2(3- 3)
=6-2 3.
6-2 3
提升能力
强化训练
矩形折叠
8.如图,在矩形ABCD中,AD=2.将∠A向内翻折,点A落在BC上,记为A ,折痕为DE.若将∠B沿EA 向内翻折,点B恰好落在DE上,记为B ,则AB=____.
A
B
D
C
B
E
A
2
60
60
60
1
1
3
3
30
30
60
60
3
提升能力
强化训练
矩形折叠
9.把一张宽为1cm的长方形纸片ABCD折叠成如图中阴影部分所示的形状,顶点A,D的对应点A ,D 互相重合,中间空白部分是以E为直角顶点,腰长为2cm的等腰直角三角形,则纸片的长AD(单位cm)为( )
A.7+3 B.7+4 C.8+3 D.8+4
A
A (D )
B
C
D
E
2
2
1
1
1
2
2
2 2
1
1
D
直角三角形
提升能力
强化训练
矩形折叠
10.如图,把某矩形纸片ABCD沿EF,GH折叠,使点B和点C落在AD边上同一点P处,点A的对称点为点A ,点D的对称点为点D ,若∠FPG=90 ,△A EP的面积为4,△D PH的面积为1,则矩形ABCD的面积等于______.
A
P
G
F
D
A
H
E
D
C
B
【分析】求矩形面积,考虑能否把矩形相邻两边都算出来.两端往中间折叠,则可得:A P=D P.
∵∠FPG=90 ,
∴A PD =90 ,
易证△A EP∽△D PH.
考虑两三角形面积分别是4和1,
∴相似比为2:1.
设AB=a,则A P=D P=a,D H=0.5a,A E=2a,
EP= a,PH= a
5
5
2
表示△D PH面积: · ·a=1,
1
2
a
2
解得a=2.
AD=2a+ a+ a+ =5+3 ,
5
5
2
a
2
5
∵AB=2.
∴矩形ABCD面积为2×(5+3 )=10+6 .
5
5
提升能力
强化训练
矩形折叠
11.如图,正方形纸片ABCD的边长为12,E是边CD上一点,连接AE、折叠该纸片,使点A落在AE上的G点,并使折痕经过点B,得到折痕BF,点F在AD上,若DE=5,则GE的长为____.
A
G
F
E
D
C
B
12
5
5
5
60
13
49
13
等积
提升能力
强化训练
矩形折叠
同课章节目录
