专题1.3平分---角平分线的四种模型-中考数学二轮复习必会几何模型剖析(全国通用)
文档属性
| 名称 | 专题1.3平分---角平分线的四种模型-中考数学二轮复习必会几何模型剖析(全国通用) |  | |
| 格式 | pptx | ||
| 文件大小 | 7.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-25 09:36:10 | ||
图片预览










文档简介
(共30张PPT)
专题一 平分模型
§1.2 与“角平分线”有关的模型
人教版中考第二轮总复习---几何模型
模型 图形示例 模型分析
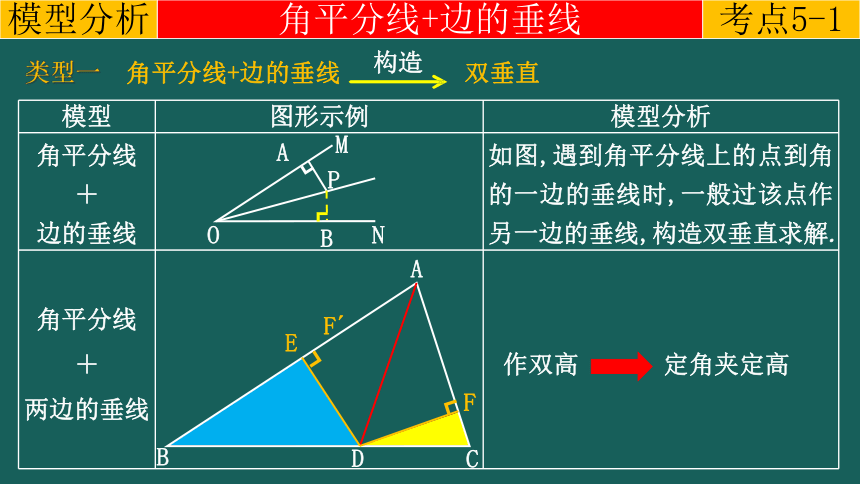
角平分线 + 边的垂线 如图,遇到角平分线上的点到角的一边的垂线时,一般过该点作另一边的垂线,构造双垂直求解.
角平分线 + 两边的垂线
考点5-1
模型分析
角平分线+边的垂线
类型一 角平分线+边的垂线
构造
双垂直
O
A
P
N
B
M
A
D
C
B
E
F
F
作双高
定角夹定高
∴AB=OC=9,BC=OA=12.
【例1】如图3,在平面直角坐标系中,矩形OABC的顶点A在x轴的正半轴上,顶点C在y轴的正半轴上,OA=12,OC=9,连接AC.
(1)填空:点B的坐标为_______;AC的长度为____.
(2)若CD平分∠ACO,交x轴于点D,求直线CD的函数表达式.
图3
A
D
O
C
B
y
x
(12,9)
15
M
∴A(12,0),B(12,9),AC= AB2+BC2= 92+122=15.
解:(1)∵四边形OABC是矩形.
∴直线CD的解析式为y=-2x+9.
(2)作DM⊥AC于M.
∵CD平分∠ACO,DO⊥CO.DM⊥AC.
∴DO=DM,∠COD=∠CMD=90 .
∵CD=CD.
∴Rt△CDO≌Rt△CDM(HL),
∴CM=OC=9.
∵AC=15.
设OD=x,则DM=x,AD=12-x.
在Rt△ADM中
∵AD =DM +AM2.
∴x2+6 =(12-x)2,
解得x=4.5.
∴D(4.5,0).
设直线CD的解析式为y=kx+b,
把C(0,9),D(4.5,0)代入得:
b=9.
0=4.5k+b
则
解得:
b=9
k=-2
∴AM=6.
考点5-1
典例精讲
角平分线+边的垂线
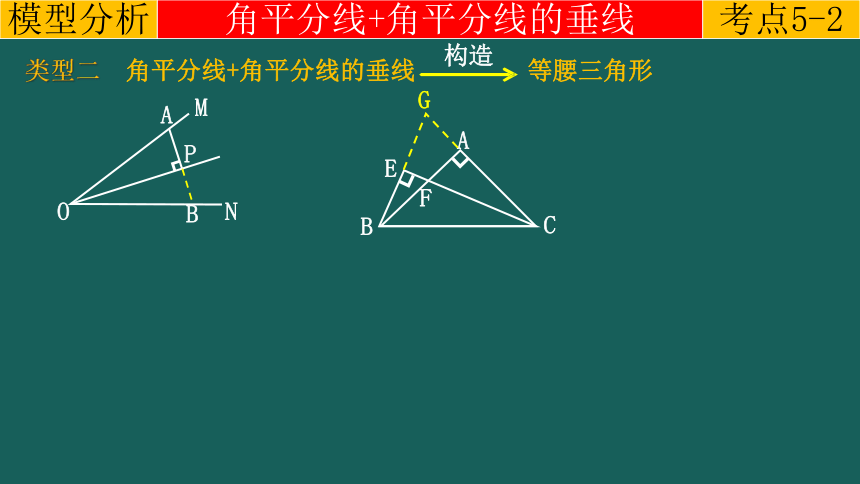
考点5-2
模型分析
角平分线+角平分线的垂线
类型二 角平分线+角平分线的垂线
构造
等腰三角形
A
O
B
P
N
M
E
F
C
B
A
G
【例2】如图,在△ABC中,∠C=90 ,AC=BC,AD平分∠BAC,BD⊥AD,若BD=2,则AE=____.
考点5-2
典例精讲
角平分线+角平分线的垂线
∴AE=BF=2BD=4.
4
F
【解析】延长BD,AC交于点F.
∵AD平分∠BAC,AD⊥BD.
∴∠ABF=∠AFB,BD=FD,BF=2BD.
∵AD⊥BD,∠ACB=90 ,∠AEC=∠BED.
∴∠EAC=∠FBC.
∵AC=BC.
∴△ACE≌△BCF.
A
B
D
E
C
图形示例 模型分析
如图,若P是∠MON平分线上一点,点A是边OM上任意一点,可考虑在边ON上 截取OB=OA,连接PB,构造△OPB≌△OPA,进而将一些线段和角进行等量代换,这是常用的解题技巧之一.
考点5-3
模型分析
见角平分线作对称
类型三 见角平分线作对称
全等三角形
构造
M
P
A
N
O
B
【例3】如图,在△ABC中,∠C=2∠B,AD平分∠BAC,求证:AB=AC+CD.
F
A
B
D
C
1
2
3
∴AB=AC+CD.
证法一:如图,在AB上截取AF,使AF=AC.
∵AD平分∠BAC,
∴∠1=∠2.
∵AD=AD
∴△AFD≌△ACD(SAS)
∴DF=DC,∠AFD=∠C.
∵∠C=2∠B.∠AFD=∠3+∠B.
∴∠3=∠B,
∴FD=FB.
∵AB=AF+FB=AC+FD.
考点5-3
典例精讲
见角平分线作对称
E
∴AB=AC+DC.
证法二:如图,延长AC到点E.使CE=DC.
∴∠CDE=∠CED.
∴∠ACB=2∠CED.
∵∠ACB=2∠B.
∴∠B=∠CED.
∴AD平分∠BAC.
∴∠1=∠2.
∵AD=AD
∴△ABD≌△AED(AAS).
∴AB=AE.
∵AE=AC+CE=AC+DC.
图形示例 模型分析
当题中同时出现角平分线和平行线时,注意找等腰三角形.一般地,角平分线,平行线,等腰三角形中任意两个条件存在,可得第三个条件(知二推一).OP平分∠MON,PQ∥ON,则△OPQ为等腰三角形.
考点5-4
模型分析
角平分线+平行线
O
M
Q
P
N
类型四 角平分线+平行线
等腰三角形
构造
【例4】如图,AC是正方形ABCD的对角线,∠DCA的平分线交BA的延长线于点E,若AB=3,则AE=______.
考点5-4
典例精讲
角平分线+平行线
E
C
D
B
A
3 2
【解析】∵AC是正方形ABCD的对角线,AB=3.
∵∠DCA的平分线交BA的延长线于点E.
∴∠DCE=∠ECA.
∵DC∥EB.
∴∠CEA=∠DCE.
∴∠CEA=∠ECA.
∴AC=3 2.
∴AE=AC=3 2.
图形示例 模型分析
夹角模型 BO平分∠ABC,CO平分∠ACB,则点O为△ABC的内心.
①S△ABC=_______________;②∠BOC=__________.
BO平分∠ABC,CO平分∠ACB,则∠O=__________.
BO平分∠ABC,CO平分∠ACB,则∠O=_____.
考点5-5
模型分析
夹角模型
A
B
C
O
E
F
A
B
C
O
E
类型五 角平分线+角平分线
三角形内心
构造
A
B
C
O
D
(AB+AC+BC)OD
1
2
90 + ∠A
1
2
90 - ∠A
1
2
∠A
1
2
【例5】如图,在Rt△ABC中,△ABC=90 ,AB=6,BC=8,∠BAC,∠ACB的平分线相交于点E,过点E作EF∥BC交AC于点F,则EF的长为( )
A. B. C. D.
考点5-5
典例精讲
夹角模型
C
B
A
E
F
C
M
D
N
∴EF=10/3
【解析】过E作ED⊥AB于D,EM⊥BC于M,EN⊥AC于N.
易得:四边形BMED是正方形,AD=AN,CM=CN.
由勾股定理得AC=10,sin∠ACB=3/5.
设BD=BM=x,则AD=AN=6-x,MC=NC=8-x.
∴AN+NC=AC.
∴6-x+8-x=10.
∴x=2.
∴BD=BM=DE=EN=2.
∵EF∥BC.
∴sin∠AFE=sin∠ACB=EN:EF=3:5
知识梳理
课堂小结
角平分线模型
当题中出现角平分线或易得到角平分线(有对称或等腰三角形)时,首先 考虑利用角平分线定理求解.若另有平行或垂直等条件,则可考虑构造等腰三角形或对称图形求解.常见类型 如下:
类型一 角平分线+边的垂线
构造
双垂直
类型二 角平分线+角平分线的垂线
构造
等腰三角形
类型三 见角平分线作对称
全等三角形
类型四 角平分线+平行线
等腰三角形
类型五 角平分线+角平分线
三角形内心
构造
构造
构造
1.如图1,Rt△ABC中,∠C=90 ,∠ABC的平分线BD交AC于点D,若CD=3,则点D到B距离DE是( )A.5 B.4 C.3 D.2
2.如图2,在△ABC中,AB=10,AC=8,∠BAC=45°,AD是∠BAC的平分线,DE⊥AB于点E,则DE的长是______.
C
B
A
E
D
C
图1
图2
A
E
D
C
B
F
M
2.作DF⊥AC,CM⊥AB,垂足分别为点F,M则DF=DE.
∵∠BAC=45 ,AC=8.
∴CM=AM=4 2.
∴S△ABC=0.5AB·CM=0.5×10×4√2=20 2.
∵S△ABC=S△ABD+S△ACD=0.5AB·DE+0.5AC·DF
=0.5DE·(AB+AC)=20 2.
20 2
9
∴DE=
20 2
9
查漏补缺
基础训练
角平分线解题策略
1.如图,△ABC中,∠BAC=90 ,S△ABC=10,AD平分∠BAC,交BC于点D,BE⊥AD交AD延长线于点E,连接CE,则△ACE的面积为___.
B
D
A
C
E
5
F
∴S△ACE=S△AEF-S△CEF=0.5S△ABF-0.5S△BCF=0.5S△ABC=5.
【解析】延长BE和AC交于点F,易得△ABF是等腰直角三角形.
∵AE⊥BF.
∴BE=EF.
查漏补缺
基础训练
角平分线解题策略
2.如图,在△ABC中,点M为BC的中点AD平分∠BAC,且BD⊥AD于点D.
求证:DM=0.5(AC-AB).
A
M
D
C
B
证明:延长BD交AC于E.
∵AD⊥BD.
∴∠ADB=∠ADE=90 .
∵AD为∠BAC的平分线.
∴∠BAD=∠EAD.
∴∠ABD=∠AEB.
∴AB=AE,BD=DE.
∵M为BC的中点.
∴DM=0.5CE=0.5(AC-AE)=0.5(AC-AB).
E
查漏补缺
基础训练
角平分线解题策略
如图,在菱形ABCD中,P是AB上的一个动点且不与A,B重合,连接DP交对角线AC于E,连接BE.求证:∠APD=∠CBE.
A
E
D
C
B
P
∴∠APD=∠CBE.
证明:∵四边形ABCD是菱形,
∴BC=CD,CA平分∠BCD.
∴∠BCE=∠DCE.
∵CE=CE,
∴△BCE≌△DCE.
∴∠CBE=∠CDE.
∵AB∥DC,
∴∠APD=∠CDE.
查漏补缺
基础训练
角平分线解题策略
1.在 ABCD中,AE平分∠BAD交边BC于点E,DF平分∠ADC交边BC于点F,若
AD=11,EF=5,则AB=______.
A
E
G
F
C
B
D
图1
A
F
E
C
B
D
图2
8或3
【解析】①如图1,在 ABCD中.
∵BC∥AD.
∴∠ADF=∠CFD.
∵DF平分∠ADC交BC于点F.
∴∠ADF=∠CDF.
∴∠CFD=∠CDF.
∴CF=CD.
同理可证AB=BE.
∴AB=BE=CF=CD.
∵EF=5,BC=AD=11.
∴BC=BE+CF-EF=2AB-EF=2AB-5=11.
∴AB=8.
∴AB=3.
②如图2,在 ABCD中,同①可得AB=BE=CF=CD.
∵EF=5.
∴BC=BE+CF+EF=2AB+EF=2AB+5=11.
查漏补缺
基础训练
角平分线解题策略
2.如图,在△ABC中,AD平分∠BAC,BD⊥AD,过D作DE∥AC,交AB于E,若AB=5,则DE= ______.
A
E
D
C
B
2.5
∴ED=0.5AB=2.5
【解析】∵AC∥ED,AD平分∠EAC.
∴∠CAD=∠ADE.∠CAD=∠EAD.
∴∠EAD=∠ADE.
∴AE=DE.
∵AD⊥BD.
∴∠BAD+∠ABD=90 .∠ADE+EDB=90 .
∴∠ABD=∠EDB.
∴BE=DE=AE.
查漏补缺
基础训练
角平分线解题策略
3.如图,在△ABC中,CD平分∠ACB交AB于D,DE∥AC交BC于点E,DF∥BC交AC于点F.求证:四边形DECF是菱形.
A
D
F
E
C
B
3
1
2
证明:如图,∵DE∥AC,DF∥BC.
∴四边形DECF为平行四边形,∠2=∠3.
∵CD平分∠ACB交AB于点D.
∴∠1=∠2.
∴∠1=∠3.
∴DE=EC.
∴四边形DECF为菱形.
查漏补缺
基础训练
角平分线解题策略
4.如图,在△ABC中,AB>AC,E为BC边的中点,AD为∠BAC的平分线,过E作AD的平行线,交AB于F,交CA的延长线于点G.
求证:BF=AC+AF.
A
D
E
F
C
B
G
Q
∴△BEF≌△CEQ(SAS).
证明:延长FE至Q,使EQ=EF,连接CQ.
∵E为BC边的中点.
∴BE=CE.
在△BEF和△CEQ中
BE=CE∠BEF=∠CEQ
EF=EQ
∴BF=CG=AG+AC=AF+AC.
∴BF=CQ,∠BFE=∠Q.
∵AD平分∠BAC.
∴∠CAD=∠BAD.
∵EF∥AD.
∴∠CAD=∠G,∠BAD=∠BFE=∠GFA.
∴∠G=∠GFA.
∴AG=AF.
∵∠BFE=∠Q.
∴∠G=∠Q.
∴CQ=CG.
∵CQ=BF.
查漏补缺
基础训练
角平分线解题策略
1.如图1,△ABC的三边AB,BC,CA的长分别是20,30,40,三条角平分线将△ABC分为三个三角形,则S△OAB∶S△OBC∶S△OAC=_______.
2.如图2,已知△ABC的周长是18cm,BO,CO分别平分∠ABC和∠ACB,OD⊥BC于点D,若△ABC的面积为45cm2,则OD=_____;若∠BOC=110°,则∠A=____.
3.如图,△ABC的外角∠ACD的平分线CP与内角∠ABC的平分线BP交于点P,若∠BPC=40 ,则∠CAP=_____ .
2:3:4
5cm
40
A
B
O
C
图1
B
A
O
C
图2
D
B
O
D
C
P
A
图3
50
查漏补缺
基础训练
角平分线解题策略
1.在△ABC中,∠ABC与∠ACB的角平分线相交于点F,过点F作DE∥BC,交AB于点D,交AC于点E,若BD+CE=9,则线段DE之长为____.
2.如图,在四边形ABCD中,AB∥DC,∠ADC的平分线与∠BCD的平分线的交点E恰好在AB上.若AD=7cm,BC=8cm,则AB的长为_____cm.
A
F
E
D
C
B
查漏补缺
基础训练
角平分线解题策略
9
A
C
D
B
E
15
3.已知等腰直角三角形ABC中,∠A=90 ,AB=AC,BD平分∠ABC,CE⊥BD,垂足为点E,求证:BD=2CE
角平分线+垂直=构造三线合一;找全等:△CAF≌△BDA
CE=EF=1/2CF=1/2DB 作辅助性的本质就是:补全图形!
A
D
E
C
B
F
查漏补缺
基础训练
角平分线解题策略
4.在△ABC中,∠A=90 ,点D在线段BC上,∠EDB=0.5∠C,BE⊥DE,垂足为点E,DE与AB相交于点F.
(1)当AB=AC时(如图1),①∠EBF=______ ;
②探究线段BE与FD的数量关系,并加以证明;
B
A
E
C
D
F
图1
解:(1)①22.5;
②FD=2BE.
证明:在△BEF和△DEB中.
∵∠E=∠E=90 ,∠EBF=∠EDB=22.5 .
∴△BEF∽△DEB.
G
作BG平分∠ABC,交DE于点G.
∴∠GDB=∠GBD=22.5 ,∠EGB=45 .
∴BG=GD,△BEG是等腰直角三角形.
设EF=x,BE=y,则BG=GD= 2y,FD= 2y+y-x.
∴FD=2BE
∵△BEF∽△DEB,
∴EF:BE=BE:DE,即:x:y=y:( 2-1)y
∴x=( 2-1)y
∴FD= 2y+y-( 2-1)y=2y
查漏补缺
基础训练
角平分线解题策略
4.在△ABC中,∠A=90 ,点D在线段BC上,∠EDB=0.5∠C,BE⊥DE,垂足为点E,DE与AB相交于点F.
(2)当AB=kAC时(如图2).求BE:FD的值(用含k的式子表示).
B
A
E
C
D
F
图2
G
N
(2)过点D作DG∥AC,交BE的延长线于点G,与BA交于点N,则∠GDB=∠C.
∵∠EDB=0.5∠C.
∴∠EDB=∠EDG.
∵BE⊥DE.
∴∠DEB=∠DEG=90 .
∵DE=DE.
∴△DEB≌△EGC(ASA)
∴BE=0.5GB.
∵∠BND=∠BNG=90 ,∠BFE=∠DFN.
∴∠EBF=∠NDF.
∴△CBN∽△FDN.
∴GB:FD=BN:DN.
∵DG∥AC,
∴△BND∽△BAC.
∴BN:BA=DN:CA.
∴BN:DN=AB:CA=k.
∴BE:FD=0.5k.
∴BE:DF=BN:2DN.
查漏补缺
基础训练
角平分线解题策略
5.已知:在△ABC中,∠ABC=60 ,∠ACB=40 ,BD平分∠ABC,CD平分∠ACB.
(1)如图1,求∠BDC的度数;
(2)如图2,连接AD,过点D作DE⊥AB于点E,
DE=2,AC=4,求△ADC的面积.
A
D
C
B
图1
解:(1)∵BD平分∠ABC.
∴∠DBC=0.5∠ABC=30 .
∵CD平分∠ACB.
∴∠DCB=0.5∠ACB=20 .
∴∠BDC=180 -∠DBC-∠DCB=130 .
∴S△ADC=0.5·AC·DF=0.5×4×2=4.
(2)过点D作DH⊥BC于点H,DF⊥ABC于点F,
∵BD平分∠ABC,CD平分∠ACB.
∴DF=DH=DE=2.
A
D
C
B
图2
E
H
F
查漏补缺
基础训练
角平分线解题策略
6.如图,△ABC中,AB=AC,AD,CD分别是两个外角的平分线.
(1)求证:AC=AD;
(2)若∠B=60 ,求证:四边形ABCD是菱形.
E
F
C
D
B
A
证明:(1)∵AB=AC.
∴∠B=∠BCA.
∵AD平分∠EAC.
∴∠EAD=∠DAC=0.5∠EAC.
∵∠B+∠BCA=∠EAC.
∴∠B=0.5∠EAD.
∴∠B=∠EAD.
∴AD∥BC.
∴∠D=∠DCF.
∵CD平分∠ACF.
∴∠ACD=∠DCF.
∴∠D=∠ACD.
∴AC=AD.
(2)∵∠B=60 ,AB=AC.
∴△ABC为等边三角形.
∴∠ACB=60 ,AB=BC.
∴∠ACF=120 .
∴∠DCF=B=60 .
∴AB∥CD.
由(1)知AD∥BC.
∴四边形ABCD是平行四边形.
∵AB=BC.
∴四边形ABCD是菱形.
查漏补缺
基础训练
角平分线解题策略
7.如图,在△ABC中,点O是AC边上(端点除外)的一个动点,过点O作直线MN∥BC.设MN交∠BCA的平分线于点E,交∠BCA的外角平分线于点F,连接AE,AF.那么当点O运动到何处时,四边形AECF是矩形 并证明你的结论.
A
O
F
E
N
M
C
B
1
2
4
5
3
∴四边形AECF是矩形.
解:当点O运动到AC的中点(或OA=OC)时,
四边形AECF是矩形.
证明:∵CE平分∠BCA.
∴∠1=∠2.
∵MN∥BC.
∴∠1=∠3.
∴∠2=∠3.
∴OE=OC.
同理,0F=OC.
∴0E=OF.
∵OA=OC.
∴四边形AECF是平行四边形.
∴OE=OC,OF=OC,OA=OC.
∴OE=OC=OF=OA,即AC=EF.
查漏补缺
基础训练
角平分线解题策略
8.如图1,将三角板放在正方形ABCD上,使三角板的直角顶点E与正方形ABCD的顶点A重合,三角板的一边交CD于点F,另一边交CB的延长线于点G.
(1)求证:EF=EG;
A(E)
F
G
D
C
B
图1
∴EF=EG.
(1)证明:∵∠DEF+∠BEF=90 ,
∠GEF=∠GEB+∠BEF=90 .
∴∠DEF=∠BEG.
在△FED和△GEB中,
∠DEF=∠BEG
ED=EB
∠D=∠EBG
∴△FED≌△GEB(ASA).
查漏补缺
基础训练
角平分线解题策略
(2)如图2,移动三角板,使顶点E始终在对角线AC上,其他条件不变,(1)中的结论是否任然成立 若成立,请给予证明;若不成立,请说明理由.
D
B
G
E
A
F
C
图2
H
P
∴EF=EG.
(2)解:仍然成立.
证明:如图,过点E作EHLBC于点H,EP⊥CD于点P.
∵四边形ABCD为正方形.
∴CE平分∠BCD.
∵EH⊥BC,EP⊥CD.
∴EH=EP.
∴四边形EHCP是正方形.
∴∠HEP=90 .
∵∠GEH+∠HEF=90 ,∠PEF+∠HEF=90 .
∴∠PEF=∠GEH.
在△FEP和△GEH中.
∠PEF=∠HEG
EP=EH
∠EPF=∠EHG
∴△FEP≌△GEH(ASA).
查漏补缺
基础训练
角平分线解题策略
专题一 平分模型
§1.2 与“角平分线”有关的模型
人教版中考第二轮总复习---几何模型
模型 图形示例 模型分析
角平分线 + 边的垂线 如图,遇到角平分线上的点到角的一边的垂线时,一般过该点作另一边的垂线,构造双垂直求解.
角平分线 + 两边的垂线
考点5-1
模型分析
角平分线+边的垂线
类型一 角平分线+边的垂线
构造
双垂直
O
A
P
N
B
M
A
D
C
B
E
F
F
作双高
定角夹定高
∴AB=OC=9,BC=OA=12.
【例1】如图3,在平面直角坐标系中,矩形OABC的顶点A在x轴的正半轴上,顶点C在y轴的正半轴上,OA=12,OC=9,连接AC.
(1)填空:点B的坐标为_______;AC的长度为____.
(2)若CD平分∠ACO,交x轴于点D,求直线CD的函数表达式.
图3
A
D
O
C
B
y
x
(12,9)
15
M
∴A(12,0),B(12,9),AC= AB2+BC2= 92+122=15.
解:(1)∵四边形OABC是矩形.
∴直线CD的解析式为y=-2x+9.
(2)作DM⊥AC于M.
∵CD平分∠ACO,DO⊥CO.DM⊥AC.
∴DO=DM,∠COD=∠CMD=90 .
∵CD=CD.
∴Rt△CDO≌Rt△CDM(HL),
∴CM=OC=9.
∵AC=15.
设OD=x,则DM=x,AD=12-x.
在Rt△ADM中
∵AD =DM +AM2.
∴x2+6 =(12-x)2,
解得x=4.5.
∴D(4.5,0).
设直线CD的解析式为y=kx+b,
把C(0,9),D(4.5,0)代入得:
b=9.
0=4.5k+b
则
解得:
b=9
k=-2
∴AM=6.
考点5-1
典例精讲
角平分线+边的垂线
考点5-2
模型分析
角平分线+角平分线的垂线
类型二 角平分线+角平分线的垂线
构造
等腰三角形
A
O
B
P
N
M
E
F
C
B
A
G
【例2】如图,在△ABC中,∠C=90 ,AC=BC,AD平分∠BAC,BD⊥AD,若BD=2,则AE=____.
考点5-2
典例精讲
角平分线+角平分线的垂线
∴AE=BF=2BD=4.
4
F
【解析】延长BD,AC交于点F.
∵AD平分∠BAC,AD⊥BD.
∴∠ABF=∠AFB,BD=FD,BF=2BD.
∵AD⊥BD,∠ACB=90 ,∠AEC=∠BED.
∴∠EAC=∠FBC.
∵AC=BC.
∴△ACE≌△BCF.
A
B
D
E
C
图形示例 模型分析
如图,若P是∠MON平分线上一点,点A是边OM上任意一点,可考虑在边ON上 截取OB=OA,连接PB,构造△OPB≌△OPA,进而将一些线段和角进行等量代换,这是常用的解题技巧之一.
考点5-3
模型分析
见角平分线作对称
类型三 见角平分线作对称
全等三角形
构造
M
P
A
N
O
B
【例3】如图,在△ABC中,∠C=2∠B,AD平分∠BAC,求证:AB=AC+CD.
F
A
B
D
C
1
2
3
∴AB=AC+CD.
证法一:如图,在AB上截取AF,使AF=AC.
∵AD平分∠BAC,
∴∠1=∠2.
∵AD=AD
∴△AFD≌△ACD(SAS)
∴DF=DC,∠AFD=∠C.
∵∠C=2∠B.∠AFD=∠3+∠B.
∴∠3=∠B,
∴FD=FB.
∵AB=AF+FB=AC+FD.
考点5-3
典例精讲
见角平分线作对称
E
∴AB=AC+DC.
证法二:如图,延长AC到点E.使CE=DC.
∴∠CDE=∠CED.
∴∠ACB=2∠CED.
∵∠ACB=2∠B.
∴∠B=∠CED.
∴AD平分∠BAC.
∴∠1=∠2.
∵AD=AD
∴△ABD≌△AED(AAS).
∴AB=AE.
∵AE=AC+CE=AC+DC.
图形示例 模型分析
当题中同时出现角平分线和平行线时,注意找等腰三角形.一般地,角平分线,平行线,等腰三角形中任意两个条件存在,可得第三个条件(知二推一).OP平分∠MON,PQ∥ON,则△OPQ为等腰三角形.
考点5-4
模型分析
角平分线+平行线
O
M
Q
P
N
类型四 角平分线+平行线
等腰三角形
构造
【例4】如图,AC是正方形ABCD的对角线,∠DCA的平分线交BA的延长线于点E,若AB=3,则AE=______.
考点5-4
典例精讲
角平分线+平行线
E
C
D
B
A
3 2
【解析】∵AC是正方形ABCD的对角线,AB=3.
∵∠DCA的平分线交BA的延长线于点E.
∴∠DCE=∠ECA.
∵DC∥EB.
∴∠CEA=∠DCE.
∴∠CEA=∠ECA.
∴AC=3 2.
∴AE=AC=3 2.
图形示例 模型分析
夹角模型 BO平分∠ABC,CO平分∠ACB,则点O为△ABC的内心.
①S△ABC=_______________;②∠BOC=__________.
BO平分∠ABC,CO平分∠ACB,则∠O=__________.
BO平分∠ABC,CO平分∠ACB,则∠O=_____.
考点5-5
模型分析
夹角模型
A
B
C
O
E
F
A
B
C
O
E
类型五 角平分线+角平分线
三角形内心
构造
A
B
C
O
D
(AB+AC+BC)OD
1
2
90 + ∠A
1
2
90 - ∠A
1
2
∠A
1
2
【例5】如图,在Rt△ABC中,△ABC=90 ,AB=6,BC=8,∠BAC,∠ACB的平分线相交于点E,过点E作EF∥BC交AC于点F,则EF的长为( )
A. B. C. D.
考点5-5
典例精讲
夹角模型
C
B
A
E
F
C
M
D
N
∴EF=10/3
【解析】过E作ED⊥AB于D,EM⊥BC于M,EN⊥AC于N.
易得:四边形BMED是正方形,AD=AN,CM=CN.
由勾股定理得AC=10,sin∠ACB=3/5.
设BD=BM=x,则AD=AN=6-x,MC=NC=8-x.
∴AN+NC=AC.
∴6-x+8-x=10.
∴x=2.
∴BD=BM=DE=EN=2.
∵EF∥BC.
∴sin∠AFE=sin∠ACB=EN:EF=3:5
知识梳理
课堂小结
角平分线模型
当题中出现角平分线或易得到角平分线(有对称或等腰三角形)时,首先 考虑利用角平分线定理求解.若另有平行或垂直等条件,则可考虑构造等腰三角形或对称图形求解.常见类型 如下:
类型一 角平分线+边的垂线
构造
双垂直
类型二 角平分线+角平分线的垂线
构造
等腰三角形
类型三 见角平分线作对称
全等三角形
类型四 角平分线+平行线
等腰三角形
类型五 角平分线+角平分线
三角形内心
构造
构造
构造
1.如图1,Rt△ABC中,∠C=90 ,∠ABC的平分线BD交AC于点D,若CD=3,则点D到B距离DE是( )A.5 B.4 C.3 D.2
2.如图2,在△ABC中,AB=10,AC=8,∠BAC=45°,AD是∠BAC的平分线,DE⊥AB于点E,则DE的长是______.
C
B
A
E
D
C
图1
图2
A
E
D
C
B
F
M
2.作DF⊥AC,CM⊥AB,垂足分别为点F,M则DF=DE.
∵∠BAC=45 ,AC=8.
∴CM=AM=4 2.
∴S△ABC=0.5AB·CM=0.5×10×4√2=20 2.
∵S△ABC=S△ABD+S△ACD=0.5AB·DE+0.5AC·DF
=0.5DE·(AB+AC)=20 2.
20 2
9
∴DE=
20 2
9
查漏补缺
基础训练
角平分线解题策略
1.如图,△ABC中,∠BAC=90 ,S△ABC=10,AD平分∠BAC,交BC于点D,BE⊥AD交AD延长线于点E,连接CE,则△ACE的面积为___.
B
D
A
C
E
5
F
∴S△ACE=S△AEF-S△CEF=0.5S△ABF-0.5S△BCF=0.5S△ABC=5.
【解析】延长BE和AC交于点F,易得△ABF是等腰直角三角形.
∵AE⊥BF.
∴BE=EF.
查漏补缺
基础训练
角平分线解题策略
2.如图,在△ABC中,点M为BC的中点AD平分∠BAC,且BD⊥AD于点D.
求证:DM=0.5(AC-AB).
A
M
D
C
B
证明:延长BD交AC于E.
∵AD⊥BD.
∴∠ADB=∠ADE=90 .
∵AD为∠BAC的平分线.
∴∠BAD=∠EAD.
∴∠ABD=∠AEB.
∴AB=AE,BD=DE.
∵M为BC的中点.
∴DM=0.5CE=0.5(AC-AE)=0.5(AC-AB).
E
查漏补缺
基础训练
角平分线解题策略
如图,在菱形ABCD中,P是AB上的一个动点且不与A,B重合,连接DP交对角线AC于E,连接BE.求证:∠APD=∠CBE.
A
E
D
C
B
P
∴∠APD=∠CBE.
证明:∵四边形ABCD是菱形,
∴BC=CD,CA平分∠BCD.
∴∠BCE=∠DCE.
∵CE=CE,
∴△BCE≌△DCE.
∴∠CBE=∠CDE.
∵AB∥DC,
∴∠APD=∠CDE.
查漏补缺
基础训练
角平分线解题策略
1.在 ABCD中,AE平分∠BAD交边BC于点E,DF平分∠ADC交边BC于点F,若
AD=11,EF=5,则AB=______.
A
E
G
F
C
B
D
图1
A
F
E
C
B
D
图2
8或3
【解析】①如图1,在 ABCD中.
∵BC∥AD.
∴∠ADF=∠CFD.
∵DF平分∠ADC交BC于点F.
∴∠ADF=∠CDF.
∴∠CFD=∠CDF.
∴CF=CD.
同理可证AB=BE.
∴AB=BE=CF=CD.
∵EF=5,BC=AD=11.
∴BC=BE+CF-EF=2AB-EF=2AB-5=11.
∴AB=8.
∴AB=3.
②如图2,在 ABCD中,同①可得AB=BE=CF=CD.
∵EF=5.
∴BC=BE+CF+EF=2AB+EF=2AB+5=11.
查漏补缺
基础训练
角平分线解题策略
2.如图,在△ABC中,AD平分∠BAC,BD⊥AD,过D作DE∥AC,交AB于E,若AB=5,则DE= ______.
A
E
D
C
B
2.5
∴ED=0.5AB=2.5
【解析】∵AC∥ED,AD平分∠EAC.
∴∠CAD=∠ADE.∠CAD=∠EAD.
∴∠EAD=∠ADE.
∴AE=DE.
∵AD⊥BD.
∴∠BAD+∠ABD=90 .∠ADE+EDB=90 .
∴∠ABD=∠EDB.
∴BE=DE=AE.
查漏补缺
基础训练
角平分线解题策略
3.如图,在△ABC中,CD平分∠ACB交AB于D,DE∥AC交BC于点E,DF∥BC交AC于点F.求证:四边形DECF是菱形.
A
D
F
E
C
B
3
1
2
证明:如图,∵DE∥AC,DF∥BC.
∴四边形DECF为平行四边形,∠2=∠3.
∵CD平分∠ACB交AB于点D.
∴∠1=∠2.
∴∠1=∠3.
∴DE=EC.
∴四边形DECF为菱形.
查漏补缺
基础训练
角平分线解题策略
4.如图,在△ABC中,AB>AC,E为BC边的中点,AD为∠BAC的平分线,过E作AD的平行线,交AB于F,交CA的延长线于点G.
求证:BF=AC+AF.
A
D
E
F
C
B
G
Q
∴△BEF≌△CEQ(SAS).
证明:延长FE至Q,使EQ=EF,连接CQ.
∵E为BC边的中点.
∴BE=CE.
在△BEF和△CEQ中
BE=CE∠BEF=∠CEQ
EF=EQ
∴BF=CG=AG+AC=AF+AC.
∴BF=CQ,∠BFE=∠Q.
∵AD平分∠BAC.
∴∠CAD=∠BAD.
∵EF∥AD.
∴∠CAD=∠G,∠BAD=∠BFE=∠GFA.
∴∠G=∠GFA.
∴AG=AF.
∵∠BFE=∠Q.
∴∠G=∠Q.
∴CQ=CG.
∵CQ=BF.
查漏补缺
基础训练
角平分线解题策略
1.如图1,△ABC的三边AB,BC,CA的长分别是20,30,40,三条角平分线将△ABC分为三个三角形,则S△OAB∶S△OBC∶S△OAC=_______.
2.如图2,已知△ABC的周长是18cm,BO,CO分别平分∠ABC和∠ACB,OD⊥BC于点D,若△ABC的面积为45cm2,则OD=_____;若∠BOC=110°,则∠A=____.
3.如图,△ABC的外角∠ACD的平分线CP与内角∠ABC的平分线BP交于点P,若∠BPC=40 ,则∠CAP=_____ .
2:3:4
5cm
40
A
B
O
C
图1
B
A
O
C
图2
D
B
O
D
C
P
A
图3
50
查漏补缺
基础训练
角平分线解题策略
1.在△ABC中,∠ABC与∠ACB的角平分线相交于点F,过点F作DE∥BC,交AB于点D,交AC于点E,若BD+CE=9,则线段DE之长为____.
2.如图,在四边形ABCD中,AB∥DC,∠ADC的平分线与∠BCD的平分线的交点E恰好在AB上.若AD=7cm,BC=8cm,则AB的长为_____cm.
A
F
E
D
C
B
查漏补缺
基础训练
角平分线解题策略
9
A
C
D
B
E
15
3.已知等腰直角三角形ABC中,∠A=90 ,AB=AC,BD平分∠ABC,CE⊥BD,垂足为点E,求证:BD=2CE
角平分线+垂直=构造三线合一;找全等:△CAF≌△BDA
CE=EF=1/2CF=1/2DB 作辅助性的本质就是:补全图形!
A
D
E
C
B
F
查漏补缺
基础训练
角平分线解题策略
4.在△ABC中,∠A=90 ,点D在线段BC上,∠EDB=0.5∠C,BE⊥DE,垂足为点E,DE与AB相交于点F.
(1)当AB=AC时(如图1),①∠EBF=______ ;
②探究线段BE与FD的数量关系,并加以证明;
B
A
E
C
D
F
图1
解:(1)①22.5;
②FD=2BE.
证明:在△BEF和△DEB中.
∵∠E=∠E=90 ,∠EBF=∠EDB=22.5 .
∴△BEF∽△DEB.
G
作BG平分∠ABC,交DE于点G.
∴∠GDB=∠GBD=22.5 ,∠EGB=45 .
∴BG=GD,△BEG是等腰直角三角形.
设EF=x,BE=y,则BG=GD= 2y,FD= 2y+y-x.
∴FD=2BE
∵△BEF∽△DEB,
∴EF:BE=BE:DE,即:x:y=y:( 2-1)y
∴x=( 2-1)y
∴FD= 2y+y-( 2-1)y=2y
查漏补缺
基础训练
角平分线解题策略
4.在△ABC中,∠A=90 ,点D在线段BC上,∠EDB=0.5∠C,BE⊥DE,垂足为点E,DE与AB相交于点F.
(2)当AB=kAC时(如图2).求BE:FD的值(用含k的式子表示).
B
A
E
C
D
F
图2
G
N
(2)过点D作DG∥AC,交BE的延长线于点G,与BA交于点N,则∠GDB=∠C.
∵∠EDB=0.5∠C.
∴∠EDB=∠EDG.
∵BE⊥DE.
∴∠DEB=∠DEG=90 .
∵DE=DE.
∴△DEB≌△EGC(ASA)
∴BE=0.5GB.
∵∠BND=∠BNG=90 ,∠BFE=∠DFN.
∴∠EBF=∠NDF.
∴△CBN∽△FDN.
∴GB:FD=BN:DN.
∵DG∥AC,
∴△BND∽△BAC.
∴BN:BA=DN:CA.
∴BN:DN=AB:CA=k.
∴BE:FD=0.5k.
∴BE:DF=BN:2DN.
查漏补缺
基础训练
角平分线解题策略
5.已知:在△ABC中,∠ABC=60 ,∠ACB=40 ,BD平分∠ABC,CD平分∠ACB.
(1)如图1,求∠BDC的度数;
(2)如图2,连接AD,过点D作DE⊥AB于点E,
DE=2,AC=4,求△ADC的面积.
A
D
C
B
图1
解:(1)∵BD平分∠ABC.
∴∠DBC=0.5∠ABC=30 .
∵CD平分∠ACB.
∴∠DCB=0.5∠ACB=20 .
∴∠BDC=180 -∠DBC-∠DCB=130 .
∴S△ADC=0.5·AC·DF=0.5×4×2=4.
(2)过点D作DH⊥BC于点H,DF⊥ABC于点F,
∵BD平分∠ABC,CD平分∠ACB.
∴DF=DH=DE=2.
A
D
C
B
图2
E
H
F
查漏补缺
基础训练
角平分线解题策略
6.如图,△ABC中,AB=AC,AD,CD分别是两个外角的平分线.
(1)求证:AC=AD;
(2)若∠B=60 ,求证:四边形ABCD是菱形.
E
F
C
D
B
A
证明:(1)∵AB=AC.
∴∠B=∠BCA.
∵AD平分∠EAC.
∴∠EAD=∠DAC=0.5∠EAC.
∵∠B+∠BCA=∠EAC.
∴∠B=0.5∠EAD.
∴∠B=∠EAD.
∴AD∥BC.
∴∠D=∠DCF.
∵CD平分∠ACF.
∴∠ACD=∠DCF.
∴∠D=∠ACD.
∴AC=AD.
(2)∵∠B=60 ,AB=AC.
∴△ABC为等边三角形.
∴∠ACB=60 ,AB=BC.
∴∠ACF=120 .
∴∠DCF=B=60 .
∴AB∥CD.
由(1)知AD∥BC.
∴四边形ABCD是平行四边形.
∵AB=BC.
∴四边形ABCD是菱形.
查漏补缺
基础训练
角平分线解题策略
7.如图,在△ABC中,点O是AC边上(端点除外)的一个动点,过点O作直线MN∥BC.设MN交∠BCA的平分线于点E,交∠BCA的外角平分线于点F,连接AE,AF.那么当点O运动到何处时,四边形AECF是矩形 并证明你的结论.
A
O
F
E
N
M
C
B
1
2
4
5
3
∴四边形AECF是矩形.
解:当点O运动到AC的中点(或OA=OC)时,
四边形AECF是矩形.
证明:∵CE平分∠BCA.
∴∠1=∠2.
∵MN∥BC.
∴∠1=∠3.
∴∠2=∠3.
∴OE=OC.
同理,0F=OC.
∴0E=OF.
∵OA=OC.
∴四边形AECF是平行四边形.
∴OE=OC,OF=OC,OA=OC.
∴OE=OC=OF=OA,即AC=EF.
查漏补缺
基础训练
角平分线解题策略
8.如图1,将三角板放在正方形ABCD上,使三角板的直角顶点E与正方形ABCD的顶点A重合,三角板的一边交CD于点F,另一边交CB的延长线于点G.
(1)求证:EF=EG;
A(E)
F
G
D
C
B
图1
∴EF=EG.
(1)证明:∵∠DEF+∠BEF=90 ,
∠GEF=∠GEB+∠BEF=90 .
∴∠DEF=∠BEG.
在△FED和△GEB中,
∠DEF=∠BEG
ED=EB
∠D=∠EBG
∴△FED≌△GEB(ASA).
查漏补缺
基础训练
角平分线解题策略
(2)如图2,移动三角板,使顶点E始终在对角线AC上,其他条件不变,(1)中的结论是否任然成立 若成立,请给予证明;若不成立,请说明理由.
D
B
G
E
A
F
C
图2
H
P
∴EF=EG.
(2)解:仍然成立.
证明:如图,过点E作EHLBC于点H,EP⊥CD于点P.
∵四边形ABCD为正方形.
∴CE平分∠BCD.
∵EH⊥BC,EP⊥CD.
∴EH=EP.
∴四边形EHCP是正方形.
∴∠HEP=90 .
∵∠GEH+∠HEF=90 ,∠PEF+∠HEF=90 .
∴∠PEF=∠GEH.
在△FEP和△GEH中.
∠PEF=∠HEG
EP=EH
∠EPF=∠EHG
∴△FEP≌△GEH(ASA).
查漏补缺
基础训练
角平分线解题策略
同课章节目录
