专题2.2轴对称---线段的最值-中考数学二轮复习必会几何模型剖析(全国通用)
文档属性
| 名称 | 专题2.2轴对称---线段的最值-中考数学二轮复习必会几何模型剖析(全国通用) |

|
|
| 格式 | pptx | ||
| 文件大小 | 9.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-25 00:00:00 | ||
图片预览






文档简介
(共22张PPT)
专题二 轴对称模型
§2.2 “将军饮马”模型
人教版中考第二轮总复习---几何模型
---线段的最值
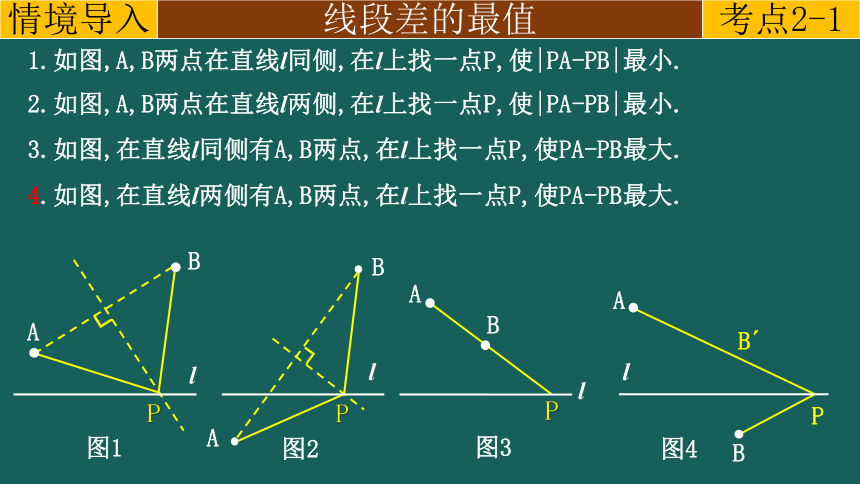
1.如图,A,B两点在直线l同侧,在l上找一点P,使|PA-PB|最小.
P
l
B
A
图1
4.如图,在直线l两侧有A,B两点,在l上找一点P,使PA-PB最大.
2.如图,A,B两点在直线l两侧,在l上找一点P,使|PA-PB|最小.
3.如图,在直线l同侧有A,B两点,在l上找一点P,使PA-PB最大.
P
l
B
A
图2
P
l
A
B
图3
B
P
B
A
l
图4
考点2-1
情境导入
线段差的最值
AB最短
B
A
①两点之间,线段最短;
核心知识
AC+BC>AB
B
A
C
②三角形两边之和大于第三边.
派生知识
考点2-1
模型分析
两点之间线段最短
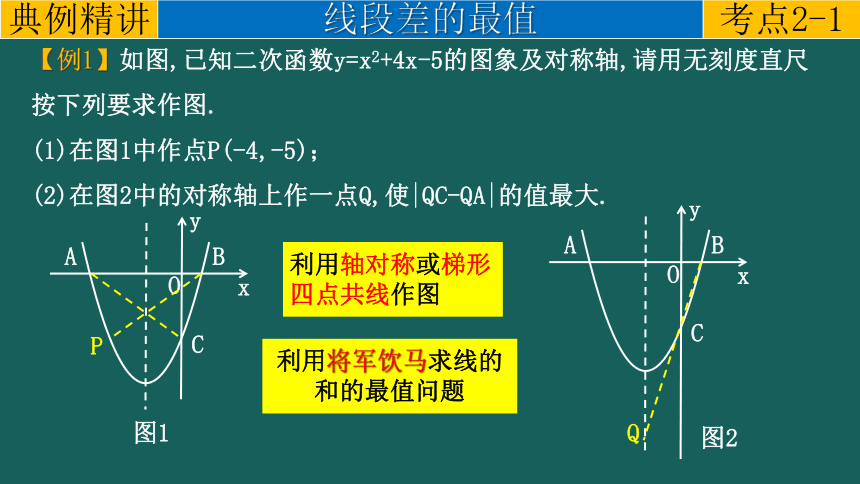
【例1】如图,已知二次函数y=x2+4x-5的图象及对称轴,请用无刻度直尺按下列要求作图.
(1)在图1中作点P(-4,-5);
(2)在图2中的对称轴上作一点Q,使|QC-QA|的值最大.
y
O
x
图1
A
B
C
P
y
O
x
图2
A
B
C
Q
利用轴对称或梯形四点共线作图
利用将军饮马求线的和的最值问题
考点2-1
典例精讲
线段差的最值
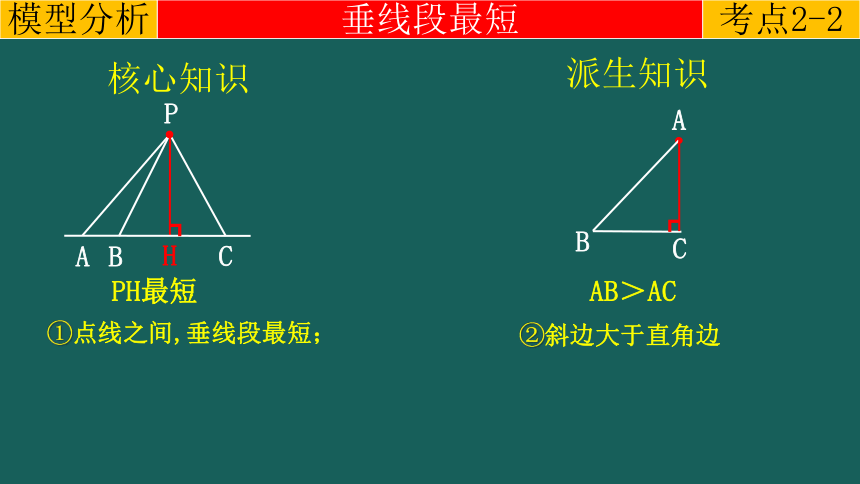
核心知识
P
H
C
B
A
PH最短
①点线之间,垂线段最短;
A
C
B
②斜边大于直角边
AB>AC
考点2-2
模型分析
垂线段最短
派生知识
【例2】如图,在Rt△ABC中∠ACB=90 ,AC=6,
BC=8,AD平分∠CAB交BC于D点,E,F分别是AD,AC上的动点,则CE+EF的最小值为_____.
A
E
F
D
B
C
F'
F
E
F
A
D
B
C
C'
F
E
E
知识点二
典例精讲
垂线段最短---一定两动
图形特征:
基本策略:
基本原理:
一定两动;
同侧化异侧、折线化直线;
垂线段最短;
将军饮马+垂线段最短
24
5
5.如图,在Rt△ABC中,∠A=90 ,BA=3,AC=4,点D是斜边BC上的一个动点,过点D分别作DM⊥AB于点M,DN⊥AC于点N,连接MN,则线段MN的最小最为____.
2.4
C
M
D
N
B
A
提升能力
强化训练
线段最值问题
6.如图,在平面直角坐标系中,⊙O的半径为,点P在经过点A(-,0)、B(0,)的直线上,PQ切⊙O于点Q,则切线长PQ的最小值为( )
A. B. C.1.2 D.1
B
y
Q
B
A
x
P
O
提升能力
强化训练
线段最值问题
8.如图,在Rt△AOB中,OB=2,∠A=30 ,⊙O的半径为1,点P是AB边上的动点,过点P作⊙O的一条切线PQ(其中点Q为切点),则线段PQ长度的最小值为______.
A
P
Q
O
B
提升能力
强化训练
与“圆”有关的最值问题
2 2
9.在⊙O中,直径AB=6,BC是弦,∠ABC=30 ,点P在BC上,点Q在⊙O上,且OP⊥PQ.
(1)如图1,当PQ∥AB时,求PQ的长度;
(2)如图2,当点P在BC上移动时,求PQ长的最大值.
A
Q
P
C
B
O
图1
A
Q
P
C
B
O
图2
6
3 3
2
如图,在Rt△ABC中,∠A=90 ,BA=3,AC=4,点D是斜边BC上的一个动点,过点D分别作DM⊥AB于点M,DN⊥AC于点N,连接MN,则线段MN的最小最为____.
2.4
C
M
D
N
B
A
提升能力
强化训练
线段最值问题
已知点O是边长为6的等边三角形ABC的中心,点P在△ABC外,△ABC,△PAB, △PBC,△PCA的面积分别记为S0,S1,S2,S3.若S1+S2+S3=2S0,则线段OP长的最小值是( )
A. B. C.3 D.
提升能力
强化训练
线段最值问题
B
P
A
C
B
O
知识梳理
课堂小结
将军饮马
将军饮马:这个将军饮的不是马,是数学!
解题依据:两点间线段最短;点到直线的垂直距离最短;翻折,对称.
解题策略:对称、翻折→化同为异;化异为同;化折为直.
两村一路(异侧)和最小
A
B
l
P
l
A
B
B
P
B
A
l
两村一路(同侧)差最大
两村一路(异侧)差最大
1.如图,边长为2的等边△ABC的两个顶点A,B分别在射线OM,ON上滑动.若OM⊥ON,则OC的最大值为______.
N
C
B
A
O
M
1+ 3
D
OC≤OD+CD
=
1+ 3
如图,在矩形ABCD中,AB=3,BC=4,点E在边AD上,且DE=3,M,N分别是边AB,BC上的动点,且BM=BN,P是线段CE上的动点,连接PM,PN.则PM+PN最小值是____,此时PC=_____.
A
N
M
P
C
D
B
N
P
x
x
4-x
4-x
x=4-x
4
2 2
1.已知A(1,1),B(4,2).
(1)点P为x轴上一动点,求PA+PB的最小值和此时P点的坐标;
(2)点P为x轴上一动点,求|PA-PB|的值最大时P点的坐标;
(3)CD为x轴上一条动线段,且CD=1,求AC+CD+DB的最小值和此时C点的坐标.
A
P
P(2,0)
A
O
y
x
B
A
O
y
x
B
P
(-2,0)
B
A
D
C
D
C
A
O
y
x
B
C(5/3,0)
提升能力
强化训练
线段最值问题
PA+PB的最小值为 ,
3 2
AC+CD+DB的最小值为 ,
13+1
2.如图,在平面直角坐标系中,一次函数y1=kx+b(k≠0)的图象与反比例函数y2=(m≠0)交于点A(3,5),B(a,-3).
(1)求该反比例函数和一次函数的解析式;
(2)在y轴上找一点P使PB-PC最大,
求PB-PC的最大值及点P的坐标.
提升能力
强化训练
线段最值问题
y
O
x
A
C
B
(1)y1=x+2,y2=
15
x
(2)P(0,2),PB-PC的最大值为
3 2
3.如图,△ABC为等边三角形,边长为6,AD⊥BC,垂足为点D,点E和点F分别是线段AD和AB上的两个动点,连接CE,EF,则CE+EF的最小值为____.
H
F
A
C
D
B
F
E
E
提升能力
强化训练
线段最值问题
垂线段最短---一定两动
3 3
4.如图,∠BAC=30 ,M为AC上一点,AM=2,点P是AB上的一动点,PQ⊥AC,垂足为点Q,则PM+PQ的最小值为____.
B
C
M
A
P
Q
N
Q
P
提升能力
强化训练
线段最值问题
垂线段最短---一定两动
【解析】如图,作M关于直线AB的对称点N,
∴NP=MP,PM+PQ=NP+PQ.
如图,当NO⊥AC时,PM+PQ取最小值.
易得∠N=∠BAC=30 ,MD=0.5AM=1.
∴MN=2,NQ=MN·cosN=2× =
3
2
3
3
5.如图,在矩形ABCD中,AD=4,∠DAC=30 ,点P,E分别在AC,AD上,则PE+PD的最小值是_______.
A
D
C
B
2 3
【解析】如图,作点D关于直线AC的对称点D
当D ,P,E三点共线,且D E⊥AD时,PE+PD最小.
∠ADD =60 ,DD =4,
易得CD=
4 3
3
∴D E=2 3.
提升能力
强化训练
线段最值问题
P
E
E
P
D
6.如图,在矩形ABCD中,AB=3,AD=4,连接AC,O是AC的中点,M是AD上一 点,且MD=1,P是BC上一动点,则PM-PO的最大值为( )
A. B. C. D.3
7.如图,已知△ABC为等腰直角三角形,AC=BC=4,∠BCD=15 ,P为CD上的动点,则|PA-PB|的最大值为( )
A. 3 B. 4 C.5 D.
A
B
D
M
O
A
P
C
提升能力
强化训练
线段最值问题
B
A
P
D
B
C
A
图2
P
C
B
Q
R
8.在△ABC中AB=10,∠BAC=45 ,∠ABC=60 .
(1)如图1,P是BC边上一动点,点P关于AB,AC的对称点分别是D,E,连接AP,AD,
AE,DE,请写出AP与DE的数量关系,并说明理由;
(2)如图2,若P,Q,R分别是BC,AB,AC上的动点,则C△PQR的最小值为_____.
(3)如图3,正方形ABCD的边长为2,E,F分别是BC,DC上的动点,且∠EAF=45 ,
P,Q,R分别是△AEF的边AE,EF,AF上的动点,求出△PQR的周长的最小值.
提升能力
强化训练
线段最值问题
A
图1
P
C
B
E
D
A
图3
Q
R
P
F
E
D
C
B
E
D
∴DE= 2AD= 2AP.
C△PQR=PQ+QR+RP
=DQ+QR+RE
≤DE= 2AP
H
≤ 2AH
= 2·ABsinB
=5 6
5 6
H
C△PQR≤ 2AH
C△PQR≤ 2AB
=2 2
同(2)可得
由半角模型可得:AH=AB
专题二 轴对称模型
§2.2 “将军饮马”模型
人教版中考第二轮总复习---几何模型
---线段的最值
1.如图,A,B两点在直线l同侧,在l上找一点P,使|PA-PB|最小.
P
l
B
A
图1
4.如图,在直线l两侧有A,B两点,在l上找一点P,使PA-PB最大.
2.如图,A,B两点在直线l两侧,在l上找一点P,使|PA-PB|最小.
3.如图,在直线l同侧有A,B两点,在l上找一点P,使PA-PB最大.
P
l
B
A
图2
P
l
A
B
图3
B
P
B
A
l
图4
考点2-1
情境导入
线段差的最值
AB最短
B
A
①两点之间,线段最短;
核心知识
AC+BC>AB
B
A
C
②三角形两边之和大于第三边.
派生知识
考点2-1
模型分析
两点之间线段最短
【例1】如图,已知二次函数y=x2+4x-5的图象及对称轴,请用无刻度直尺按下列要求作图.
(1)在图1中作点P(-4,-5);
(2)在图2中的对称轴上作一点Q,使|QC-QA|的值最大.
y
O
x
图1
A
B
C
P
y
O
x
图2
A
B
C
Q
利用轴对称或梯形四点共线作图
利用将军饮马求线的和的最值问题
考点2-1
典例精讲
线段差的最值
核心知识
P
H
C
B
A
PH最短
①点线之间,垂线段最短;
A
C
B
②斜边大于直角边
AB>AC
考点2-2
模型分析
垂线段最短
派生知识
【例2】如图,在Rt△ABC中∠ACB=90 ,AC=6,
BC=8,AD平分∠CAB交BC于D点,E,F分别是AD,AC上的动点,则CE+EF的最小值为_____.
A
E
F
D
B
C
F'
F
E
F
A
D
B
C
C'
F
E
E
知识点二
典例精讲
垂线段最短---一定两动
图形特征:
基本策略:
基本原理:
一定两动;
同侧化异侧、折线化直线;
垂线段最短;
将军饮马+垂线段最短
24
5
5.如图,在Rt△ABC中,∠A=90 ,BA=3,AC=4,点D是斜边BC上的一个动点,过点D分别作DM⊥AB于点M,DN⊥AC于点N,连接MN,则线段MN的最小最为____.
2.4
C
M
D
N
B
A
提升能力
强化训练
线段最值问题
6.如图,在平面直角坐标系中,⊙O的半径为,点P在经过点A(-,0)、B(0,)的直线上,PQ切⊙O于点Q,则切线长PQ的最小值为( )
A. B. C.1.2 D.1
B
y
Q
B
A
x
P
O
提升能力
强化训练
线段最值问题
8.如图,在Rt△AOB中,OB=2,∠A=30 ,⊙O的半径为1,点P是AB边上的动点,过点P作⊙O的一条切线PQ(其中点Q为切点),则线段PQ长度的最小值为______.
A
P
Q
O
B
提升能力
强化训练
与“圆”有关的最值问题
2 2
9.在⊙O中,直径AB=6,BC是弦,∠ABC=30 ,点P在BC上,点Q在⊙O上,且OP⊥PQ.
(1)如图1,当PQ∥AB时,求PQ的长度;
(2)如图2,当点P在BC上移动时,求PQ长的最大值.
A
Q
P
C
B
O
图1
A
Q
P
C
B
O
图2
6
3 3
2
如图,在Rt△ABC中,∠A=90 ,BA=3,AC=4,点D是斜边BC上的一个动点,过点D分别作DM⊥AB于点M,DN⊥AC于点N,连接MN,则线段MN的最小最为____.
2.4
C
M
D
N
B
A
提升能力
强化训练
线段最值问题
已知点O是边长为6的等边三角形ABC的中心,点P在△ABC外,△ABC,△PAB, △PBC,△PCA的面积分别记为S0,S1,S2,S3.若S1+S2+S3=2S0,则线段OP长的最小值是( )
A. B. C.3 D.
提升能力
强化训练
线段最值问题
B
P
A
C
B
O
知识梳理
课堂小结
将军饮马
将军饮马:这个将军饮的不是马,是数学!
解题依据:两点间线段最短;点到直线的垂直距离最短;翻折,对称.
解题策略:对称、翻折→化同为异;化异为同;化折为直.
两村一路(异侧)和最小
A
B
l
P
l
A
B
B
P
B
A
l
两村一路(同侧)差最大
两村一路(异侧)差最大
1.如图,边长为2的等边△ABC的两个顶点A,B分别在射线OM,ON上滑动.若OM⊥ON,则OC的最大值为______.
N
C
B
A
O
M
1+ 3
D
OC≤OD+CD
=
1+ 3
如图,在矩形ABCD中,AB=3,BC=4,点E在边AD上,且DE=3,M,N分别是边AB,BC上的动点,且BM=BN,P是线段CE上的动点,连接PM,PN.则PM+PN最小值是____,此时PC=_____.
A
N
M
P
C
D
B
N
P
x
x
4-x
4-x
x=4-x
4
2 2
1.已知A(1,1),B(4,2).
(1)点P为x轴上一动点,求PA+PB的最小值和此时P点的坐标;
(2)点P为x轴上一动点,求|PA-PB|的值最大时P点的坐标;
(3)CD为x轴上一条动线段,且CD=1,求AC+CD+DB的最小值和此时C点的坐标.
A
P
P(2,0)
A
O
y
x
B
A
O
y
x
B
P
(-2,0)
B
A
D
C
D
C
A
O
y
x
B
C(5/3,0)
提升能力
强化训练
线段最值问题
PA+PB的最小值为 ,
3 2
AC+CD+DB的最小值为 ,
13+1
2.如图,在平面直角坐标系中,一次函数y1=kx+b(k≠0)的图象与反比例函数y2=(m≠0)交于点A(3,5),B(a,-3).
(1)求该反比例函数和一次函数的解析式;
(2)在y轴上找一点P使PB-PC最大,
求PB-PC的最大值及点P的坐标.
提升能力
强化训练
线段最值问题
y
O
x
A
C
B
(1)y1=x+2,y2=
15
x
(2)P(0,2),PB-PC的最大值为
3 2
3.如图,△ABC为等边三角形,边长为6,AD⊥BC,垂足为点D,点E和点F分别是线段AD和AB上的两个动点,连接CE,EF,则CE+EF的最小值为____.
H
F
A
C
D
B
F
E
E
提升能力
强化训练
线段最值问题
垂线段最短---一定两动
3 3
4.如图,∠BAC=30 ,M为AC上一点,AM=2,点P是AB上的一动点,PQ⊥AC,垂足为点Q,则PM+PQ的最小值为____.
B
C
M
A
P
Q
N
Q
P
提升能力
强化训练
线段最值问题
垂线段最短---一定两动
【解析】如图,作M关于直线AB的对称点N,
∴NP=MP,PM+PQ=NP+PQ.
如图,当NO⊥AC时,PM+PQ取最小值.
易得∠N=∠BAC=30 ,MD=0.5AM=1.
∴MN=2,NQ=MN·cosN=2× =
3
2
3
3
5.如图,在矩形ABCD中,AD=4,∠DAC=30 ,点P,E分别在AC,AD上,则PE+PD的最小值是_______.
A
D
C
B
2 3
【解析】如图,作点D关于直线AC的对称点D
当D ,P,E三点共线,且D E⊥AD时,PE+PD最小.
∠ADD =60 ,DD =4,
易得CD=
4 3
3
∴D E=2 3.
提升能力
强化训练
线段最值问题
P
E
E
P
D
6.如图,在矩形ABCD中,AB=3,AD=4,连接AC,O是AC的中点,M是AD上一 点,且MD=1,P是BC上一动点,则PM-PO的最大值为( )
A. B. C. D.3
7.如图,已知△ABC为等腰直角三角形,AC=BC=4,∠BCD=15 ,P为CD上的动点,则|PA-PB|的最大值为( )
A. 3 B. 4 C.5 D.
A
B
D
M
O
A
P
C
提升能力
强化训练
线段最值问题
B
A
P
D
B
C
A
图2
P
C
B
Q
R
8.在△ABC中AB=10,∠BAC=45 ,∠ABC=60 .
(1)如图1,P是BC边上一动点,点P关于AB,AC的对称点分别是D,E,连接AP,AD,
AE,DE,请写出AP与DE的数量关系,并说明理由;
(2)如图2,若P,Q,R分别是BC,AB,AC上的动点,则C△PQR的最小值为_____.
(3)如图3,正方形ABCD的边长为2,E,F分别是BC,DC上的动点,且∠EAF=45 ,
P,Q,R分别是△AEF的边AE,EF,AF上的动点,求出△PQR的周长的最小值.
提升能力
强化训练
线段最值问题
A
图1
P
C
B
E
D
A
图3
Q
R
P
F
E
D
C
B
E
D
∴DE= 2AD= 2AP.
C△PQR=PQ+QR+RP
=DQ+QR+RE
≤DE= 2AP
H
≤ 2AH
= 2·ABsinB
=5 6
5 6
H
C△PQR≤ 2AH
C△PQR≤ 2AB
=2 2
同(2)可得
由半角模型可得:AH=AB
同课章节目录
