专题3.2旋转---三叉口模型-中考数学二轮复习必会几何模型剖析(全国通用)
文档属性
| 名称 | 专题3.2旋转---三叉口模型-中考数学二轮复习必会几何模型剖析(全国通用) |  | |
| 格式 | pptx | ||
| 文件大小 | 6.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-25 09:42:29 | ||
图片预览





文档简介
(共16张PPT)
专题三 全等模型---旋转
§3.2 “三叉口”模型
人教版中考第二轮总复习---几何模型
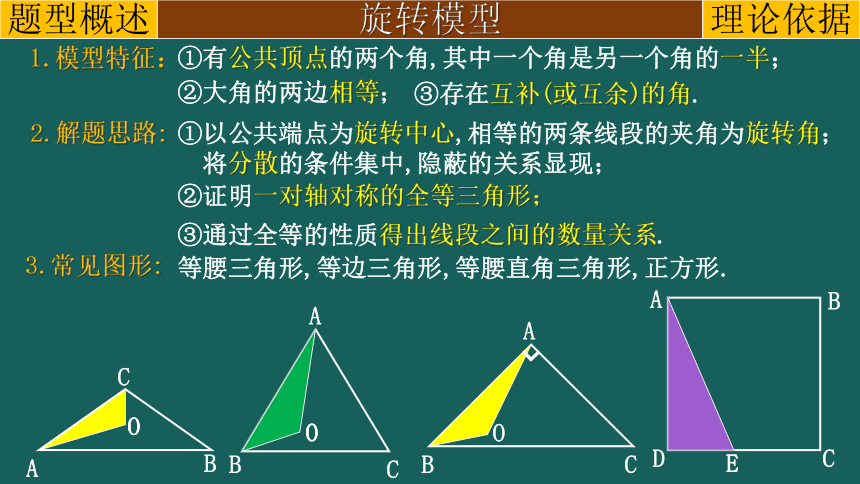
1.模型特征:
①有公共顶点的两个角,其中一个角是另一个角的一半;
②大角的两边相等;
③存在互补(或互余)的角.
2.解题思路:
③通过全等的性质得出线段之间的数量关系.
①以公共端点为旋转中心,相等的两条线段的夹角为旋转角;
将分散的条件集中,隐蔽的关系显现;
②证明一对轴对称的全等三角形;
理论依据
题型概述
旋转模型
3.常见图形:
等腰三角形,等边三角形,等腰直角三角形,正方形.
O
O
C
B
A
A
O
C
B
O
A
B
C
D
E
E
A
O
C
B
【例1】如图,点P在等边△ABC的内部,且PC=6,PA=8,PB=10,将线段PC绕点C顺时针旋转60 得到DC,连接AD,则
(1)sin∠PAD的值为____;
(2)则四边形APBD的面积为________.
(3)S△ABP+S△BPC=_________.
解:(1)连接PD,
∴sin∠PAD=3/5
则△CPD是等边三角形,故PD=PC=6
易证△CPB≌△CDA
∴AD=BP=10
又∵AP=8,
∴△APD是直角三角形,
(2)S四边形APBD=S△APD+S△PCD
(3)S△APO+S△BPC
=S△AEP+S△BEP
考点2-1
典例精讲
三叉口模型---等边三角形
A
C
B
P
D
D
5
3
24+9 3
24+25 3
A
C
B
P
D
A
C
B
P
D
A
C
B
P
E
A
C
B
P
F
【小结】如果说(1)(2)问是给出了辅助线,那么第(3)问便是完全自行构造旋转,这个图形也是一个固定搭配.
【搭配一】若PA2+PC2=PB2,则可任意旋转,得等边+直角.
且两条较短边夹角(∠APC)为150 .
【搭配二】若∠APC=150 ,则有PA2+PC2=PB2.
考点2-1
模型分析
三叉口模型---等边三角形
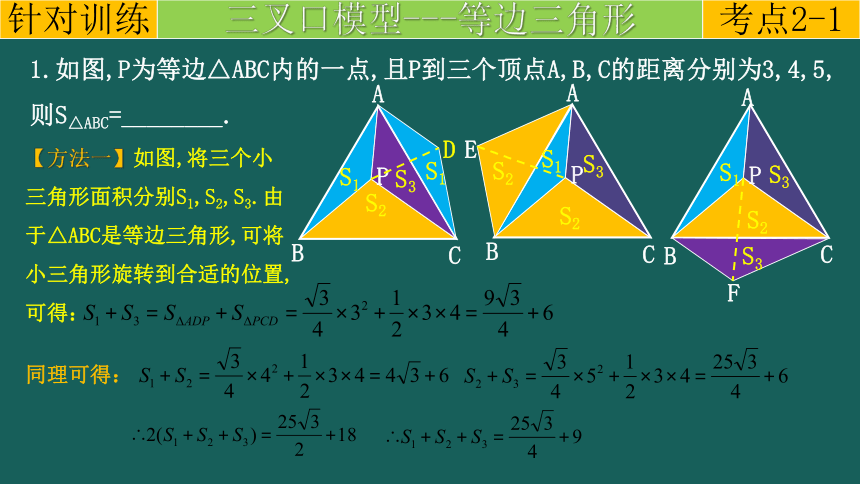
1.如图,P为等边△ABC内的一点,且P到三个顶点A,B,C的距离分别为3,4,5,则S△ABC=________.
【方法一】如图,将三个小三角形面积分别S1,S2,S3.由于△ABC是等边三角形,可将小三角形旋转到合适的位置,可得:
考点2-1
针对训练
三叉口模型---等边三角形
A
P
C
B
D
S1
S3
S2
S1
A
P
C
B
E
S1
S3
S2
S2
A
P
C
B
F
S1
S3
S2
S3
同理可得:
【方法二】如图,易证∠APB=150 ,过点A作BP的垂线交BP延长线于点H,
A
P
C
B
H
考点2-1
针对训练
三叉口模型---等边三角形
1.如图,P为等边△ABC内的一点,且P到三个顶点A,B,C的距离分别为3,4,5,则S△ABC=________.
2.如图,点P为等边△ABC内一点,且PA=5,PB=3,PC=4,
(1)求∠BPC的度数;(2)求等边△ABC的边长;(3)求等边△ABC的面积.
解:(1)∵△ABC是等边三角形,
∴P B=PB=3,P C=PA=5,∠PBP =ABC=60 .
P
H
A
P
C
B
3
4
5
将△ABP绕点B顺时针旋转60 得△CBQ,
∴AB=BC,∠ABC60 .
∴△PBP 为等边三角形.
∴△PBP 为等边三角形.
∴PP =PB=3,∠BPP =60 .
∵32+42=52.
即P P2+PC2=P C2.
∴∠P PC=90 .
∴∠BPC=∠BPP +∠P PC=150 .
(2)过点B作BH⊥PC于点H.
连接PQ.
∵∠BPC=150 .
∴∠BPH=30 .
∴BH=0.5BP=1.5.
(3)S△ABC=
三线共点必旋转
考点2-1
针对训练
三叉口模型---等边三角形
【例2】如图,点P是正方形ABCD内一点,PA=,PD=2,PC=.
(1)求∠APD的大小; (2)求正方形边长.
【思路点拨】
(1)将△APD绕点D逆时针旋转90 得△CQD,再连接PQ,
(2)作CH⊥DQ于点H,
求得∠APD=∠CQD=45 +90 =135°
三线共点必旋转
考点2-2
典例精讲
三叉口模型---正方形
A
P
D
C
B
H
Q
求得CH=HQ=1,再由勾股定理得出CD=
10
已知在△ACB中,∠ACB=90 ,AC=BC,PA=3,PC=2,PB=1,则∠BPC=______.
A
P
B
C
P
135
三叉口模型---三线共点必旋转
考点2-2
针对训练
三叉口模型---等腰直角三角形
【思考】如果放在正方形里,条件与结论又该如何搭配 作旋转之后,可得△AEP是等腰直角三角形,若使△PEB也为直角三角形,则∠APD=135 ,而线段PA,PB,PD之间的关系为2PA2+PD2=PB2.
【搭配一】若∠APD=135 ,则2PA2+PD2=PB2
【搭配二】若2PA2+PD2=PB2,则∠APD=135
A
P
D
C
B
E
F
考点2-2
模型分析
三叉口模型---正方形
知识梳理
课堂小结
三叉口模型
1.三叉口模型的特征:
①在正多边形(或等腰直角三角形)中;
②三条已知线段有公共端点;
2.解题思路:
③由旋转的性质和勾股定理的逆定理求出角度;
①将其中一个三角形到旋转;
②连接三叉口点与其对应点;
④过正多边形的顶点作求出角的一边的垂线.
⑤利用勾股定理求出正多边形的边长(或面积).
【例2】在Rt△ABC中,AB=AC,点P是三角形内一点且∠APB=135 ,PC=,AC的最大值为_______.
A
P
C
B
知识点二
典例精讲
三叉口模型---等腰直角三角形
P
A
P
B
C
D
E
F
8
10
H
如图,点P为正六边形ABCDEF内一点,且PA=8,PB=3,PC=10,则正六边形ABCD的面积为_________.
提升能力
强化训练
三叉口模型---正多边形
三线共点必旋转
100+24 2
3 2
1.已知P为等边三角形ABC的边BC上的一点,若∠APC=104 ,则在以线段AP、BP、CP为边的三角形中,最小内角的大小为( ) A.14 B.16 C.24 D.26
B
A
C
B
P
Q
A
C
B
P
P
2.阅读材料:小明喜欢探究数学问题,一天杨老师给他一道几何问题:如图1,△ABC和△BDE都是等边三角形,且点A在DE上.求证:以AE,AD,AC为边的三角形是钝角三角形.
探究发现:(1)小明通过探究发现:连接DC.根据已知条件,可以证明DC=AE,∠ADC=120 ,从而得出△ADC是钝角三角形,故以AE,AD,AC为边的三角形是钝角三角形.请你根据小明的思路,写出完整的证明过程;
A
D
E
C
B
图1
(1)证明:如图1,连接DC.
∴以AE,AD,AC为边的三角形是钝角三角形.
∵△ABC和△BDE都是等边三角形.
∴AB=CB,BD=BE,∠ABC=∠DBE=∠E=∠BDE=60 .
∴∠ABC-∠ABD=∠DBE-∠ABD,即∠CBD=∠ABE.
∴△CBD≌△ABE(SAS).
∴CD=AE,∠BDC=∠E=60 .
∴∠ADC=∠BDE+∠BDC=120 .
∴△ADC为钝角三角形.
拓展迁移:(2)如图2,四边形ABCD和四边形BGFE都是正方形,且点A在EG上.
①试猜想:以AE,AG,AC为边的三角形的形状,并说明理由;
②若AE2+AG2=10,试求出正方形ABCD的面积.
A
E
G
D
C
B
F
图2
故以AE,AG,AC为边的三角形是直角三角形.
(2)解:①以AE,AG,AC为边的三角形是直角三角形.理由如下:如图2,连接CG.
∵四边形ABCD和四边形BGFE都是正方形.
∴AB=CB,BE=BG,∠ABC=∠EBG=90 ,∠EGB=∠GEB=45 .
∴∠ABC-∠ABG=∠EBG-∠ABG,即∠CBG=∠ABE.
∴△CBG≌△ABE(SAS).
∴CG=AE,∠CGB=∠AEB=45 .
∴∠AGC=∠EGB+∠CGB=45 +45 =90 ,
∴△ACG是直角三角形,
∴CG2+AG2=AC2,
∴AE2+AG2=AC2.
∴S正方形ABCD=0.5AC2=5.
②由①可知,AE2+AG2=AC2.
∵AE2+AG2=10.
∴AC2=10.
专题三 全等模型---旋转
§3.2 “三叉口”模型
人教版中考第二轮总复习---几何模型
1.模型特征:
①有公共顶点的两个角,其中一个角是另一个角的一半;
②大角的两边相等;
③存在互补(或互余)的角.
2.解题思路:
③通过全等的性质得出线段之间的数量关系.
①以公共端点为旋转中心,相等的两条线段的夹角为旋转角;
将分散的条件集中,隐蔽的关系显现;
②证明一对轴对称的全等三角形;
理论依据
题型概述
旋转模型
3.常见图形:
等腰三角形,等边三角形,等腰直角三角形,正方形.
O
O
C
B
A
A
O
C
B
O
A
B
C
D
E
E
A
O
C
B
【例1】如图,点P在等边△ABC的内部,且PC=6,PA=8,PB=10,将线段PC绕点C顺时针旋转60 得到DC,连接AD,则
(1)sin∠PAD的值为____;
(2)则四边形APBD的面积为________.
(3)S△ABP+S△BPC=_________.
解:(1)连接PD,
∴sin∠PAD=3/5
则△CPD是等边三角形,故PD=PC=6
易证△CPB≌△CDA
∴AD=BP=10
又∵AP=8,
∴△APD是直角三角形,
(2)S四边形APBD=S△APD+S△PCD
(3)S△APO+S△BPC
=S△AEP+S△BEP
考点2-1
典例精讲
三叉口模型---等边三角形
A
C
B
P
D
D
5
3
24+9 3
24+25 3
A
C
B
P
D
A
C
B
P
D
A
C
B
P
E
A
C
B
P
F
【小结】如果说(1)(2)问是给出了辅助线,那么第(3)问便是完全自行构造旋转,这个图形也是一个固定搭配.
【搭配一】若PA2+PC2=PB2,则可任意旋转,得等边+直角.
且两条较短边夹角(∠APC)为150 .
【搭配二】若∠APC=150 ,则有PA2+PC2=PB2.
考点2-1
模型分析
三叉口模型---等边三角形
1.如图,P为等边△ABC内的一点,且P到三个顶点A,B,C的距离分别为3,4,5,则S△ABC=________.
【方法一】如图,将三个小三角形面积分别S1,S2,S3.由于△ABC是等边三角形,可将小三角形旋转到合适的位置,可得:
考点2-1
针对训练
三叉口模型---等边三角形
A
P
C
B
D
S1
S3
S2
S1
A
P
C
B
E
S1
S3
S2
S2
A
P
C
B
F
S1
S3
S2
S3
同理可得:
【方法二】如图,易证∠APB=150 ,过点A作BP的垂线交BP延长线于点H,
A
P
C
B
H
考点2-1
针对训练
三叉口模型---等边三角形
1.如图,P为等边△ABC内的一点,且P到三个顶点A,B,C的距离分别为3,4,5,则S△ABC=________.
2.如图,点P为等边△ABC内一点,且PA=5,PB=3,PC=4,
(1)求∠BPC的度数;(2)求等边△ABC的边长;(3)求等边△ABC的面积.
解:(1)∵△ABC是等边三角形,
∴P B=PB=3,P C=PA=5,∠PBP =ABC=60 .
P
H
A
P
C
B
3
4
5
将△ABP绕点B顺时针旋转60 得△CBQ,
∴AB=BC,∠ABC60 .
∴△PBP 为等边三角形.
∴△PBP 为等边三角形.
∴PP =PB=3,∠BPP =60 .
∵32+42=52.
即P P2+PC2=P C2.
∴∠P PC=90 .
∴∠BPC=∠BPP +∠P PC=150 .
(2)过点B作BH⊥PC于点H.
连接PQ.
∵∠BPC=150 .
∴∠BPH=30 .
∴BH=0.5BP=1.5.
(3)S△ABC=
三线共点必旋转
考点2-1
针对训练
三叉口模型---等边三角形
【例2】如图,点P是正方形ABCD内一点,PA=,PD=2,PC=.
(1)求∠APD的大小; (2)求正方形边长.
【思路点拨】
(1)将△APD绕点D逆时针旋转90 得△CQD,再连接PQ,
(2)作CH⊥DQ于点H,
求得∠APD=∠CQD=45 +90 =135°
三线共点必旋转
考点2-2
典例精讲
三叉口模型---正方形
A
P
D
C
B
H
Q
求得CH=HQ=1,再由勾股定理得出CD=
10
已知在△ACB中,∠ACB=90 ,AC=BC,PA=3,PC=2,PB=1,则∠BPC=______.
A
P
B
C
P
135
三叉口模型---三线共点必旋转
考点2-2
针对训练
三叉口模型---等腰直角三角形
【思考】如果放在正方形里,条件与结论又该如何搭配 作旋转之后,可得△AEP是等腰直角三角形,若使△PEB也为直角三角形,则∠APD=135 ,而线段PA,PB,PD之间的关系为2PA2+PD2=PB2.
【搭配一】若∠APD=135 ,则2PA2+PD2=PB2
【搭配二】若2PA2+PD2=PB2,则∠APD=135
A
P
D
C
B
E
F
考点2-2
模型分析
三叉口模型---正方形
知识梳理
课堂小结
三叉口模型
1.三叉口模型的特征:
①在正多边形(或等腰直角三角形)中;
②三条已知线段有公共端点;
2.解题思路:
③由旋转的性质和勾股定理的逆定理求出角度;
①将其中一个三角形到旋转;
②连接三叉口点与其对应点;
④过正多边形的顶点作求出角的一边的垂线.
⑤利用勾股定理求出正多边形的边长(或面积).
【例2】在Rt△ABC中,AB=AC,点P是三角形内一点且∠APB=135 ,PC=,AC的最大值为_______.
A
P
C
B
知识点二
典例精讲
三叉口模型---等腰直角三角形
P
A
P
B
C
D
E
F
8
10
H
如图,点P为正六边形ABCDEF内一点,且PA=8,PB=3,PC=10,则正六边形ABCD的面积为_________.
提升能力
强化训练
三叉口模型---正多边形
三线共点必旋转
100+24 2
3 2
1.已知P为等边三角形ABC的边BC上的一点,若∠APC=104 ,则在以线段AP、BP、CP为边的三角形中,最小内角的大小为( ) A.14 B.16 C.24 D.26
B
A
C
B
P
Q
A
C
B
P
P
2.阅读材料:小明喜欢探究数学问题,一天杨老师给他一道几何问题:如图1,△ABC和△BDE都是等边三角形,且点A在DE上.求证:以AE,AD,AC为边的三角形是钝角三角形.
探究发现:(1)小明通过探究发现:连接DC.根据已知条件,可以证明DC=AE,∠ADC=120 ,从而得出△ADC是钝角三角形,故以AE,AD,AC为边的三角形是钝角三角形.请你根据小明的思路,写出完整的证明过程;
A
D
E
C
B
图1
(1)证明:如图1,连接DC.
∴以AE,AD,AC为边的三角形是钝角三角形.
∵△ABC和△BDE都是等边三角形.
∴AB=CB,BD=BE,∠ABC=∠DBE=∠E=∠BDE=60 .
∴∠ABC-∠ABD=∠DBE-∠ABD,即∠CBD=∠ABE.
∴△CBD≌△ABE(SAS).
∴CD=AE,∠BDC=∠E=60 .
∴∠ADC=∠BDE+∠BDC=120 .
∴△ADC为钝角三角形.
拓展迁移:(2)如图2,四边形ABCD和四边形BGFE都是正方形,且点A在EG上.
①试猜想:以AE,AG,AC为边的三角形的形状,并说明理由;
②若AE2+AG2=10,试求出正方形ABCD的面积.
A
E
G
D
C
B
F
图2
故以AE,AG,AC为边的三角形是直角三角形.
(2)解:①以AE,AG,AC为边的三角形是直角三角形.理由如下:如图2,连接CG.
∵四边形ABCD和四边形BGFE都是正方形.
∴AB=CB,BE=BG,∠ABC=∠EBG=90 ,∠EGB=∠GEB=45 .
∴∠ABC-∠ABG=∠EBG-∠ABG,即∠CBG=∠ABE.
∴△CBG≌△ABE(SAS).
∴CG=AE,∠CGB=∠AEB=45 .
∴∠AGC=∠EGB+∠CGB=45 +45 =90 ,
∴△ACG是直角三角形,
∴CG2+AG2=AC2,
∴AE2+AG2=AC2.
∴S正方形ABCD=0.5AC2=5.
②由①可知,AE2+AG2=AC2.
∵AE2+AG2=10.
∴AC2=10.
同课章节目录
