专题2.1轴对称---将军饮马模型-中考数学二轮复习必会几何模型剖析(全国通用)
文档属性
| 名称 | 专题2.1轴对称---将军饮马模型-中考数学二轮复习必会几何模型剖析(全国通用) |  | |
| 格式 | pptx | ||
| 文件大小 | 12.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-25 09:44:31 | ||
图片预览







文档简介
(共21张PPT)
专题二 轴对称模型
§2.1 “将军饮马”模型
人教版中考第二轮总复习---几何模型
考点归纳
知识梳理
最值问题---解题策略
1.分析定点、动点,寻找不变特征;
2.确定路径(关键):
3.①若属于常见模型,调用模型解决问题;
②若不属于常见模型,要结合所求目标.
根据不变特征转化为基本定理或函数解决问题.
4.设计方案,求出路径长.
通过起点、终点、特殊点猜测运动路径(轨迹),
并结合不变特征进行验证;
线段最值
单动线段最值
双动线段最值
三动线段最值
1.点到点
2.点到线
3.点到圆
PA±PB
PA±kPB
费马点模型
PA+PB+PC
两点之间线段最短
垂线段最短
点心线截距最短(长).
将军饮马模型
胡不归模型
AB+BC+CD
将军饮马模型
考点归纳
知识梳理
线段最值问题---基本类型
考点3-1
视频导入
将军饮马---两定一动
草地
河流
M
N
B
【引例】如图,一位将军骑马从驻地A出发,先牵马去河边MN喝水,再回到驻地B.这位将军怎样走路程最短
考点3-1
情境导入
将军饮马---两定一动
A
P1
P2
P3
P
B'
将军沿A-P-B走路程最短.
PA+PB=_______=____.
PA+PB
AB
P1A+P1B=_______
P1A+P1B
>AB
图形特征:
两定一动;
基本策略:
同侧化异侧、折线化直线;
基本方法:
一个动点一条河,一次对称跑不脱;
基本原理:
两点之间线段最短.
适用模型:
将军饮马;
AB最短
B
A
①两点之间,线段最短;
核心知识
AC+BC>AB
B
A
C
②三角形两边之和大于第三边.
派生知识
考点3-1
模型分析
两点之间线段最短
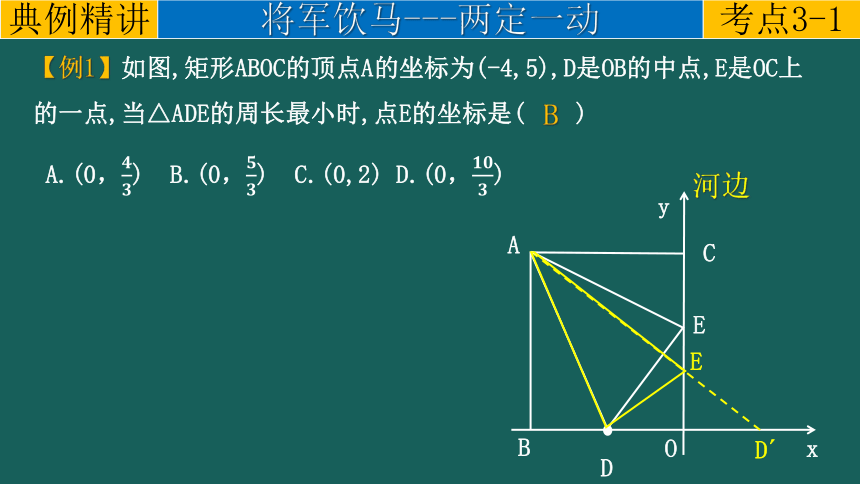
【例1】如图,矩形ABOC的顶点A的坐标为(-4,5),D是OB的中点,E是OC上的一点,当△ADE的周长最小时,点E的坐标是( )
A.(0,) B.(0,) C.(0,2) D.(0,)
B
A
D
C
B
O
x
y
E
E
D
考点3-1
典例精讲
将军饮马---两定一动
河边
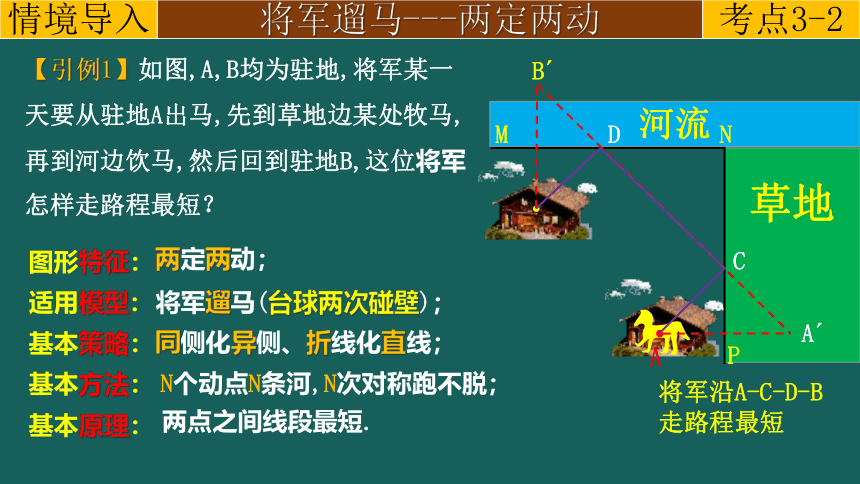
【引例1】如图,A,B均为驻地,将军某一天要从驻地A出马,先到草地边某处牧马,再到河边饮马,然后回到驻地B,这位将军怎样走路程最短?
草地
河流
P
N
M
A
将军沿A-C-D-B
走路程最短
C
D
A
B
考点3-2
情境导入
将军遛马---两定两动
图形特征:
两定两动;
基本策略:
同侧化异侧、折线化直线;
基本方法:
N个动点N条河,N次对称跑不脱;
基本原理:
两点之间线段最短.
适用模型:
将军遛马(台球两次碰壁);
【例2-1】如图,点A(a,3)B(b,1)都在双曲线y=上,点C,D分别是x轴,y轴上的动点,则四边形ABCD周长的最小值为( )
A.5 B.6 C.2+2 D.8
B
A
D
B
C
y
x
O
A'
B'
D
C
考点3-2
典例精讲
将军遛马---两定两动
河边
草地
草地
河流
N
M
O
【引例2】如图,一位将军骑马从驻地A出发,先牵马去草地OM吃草,再牵马去河边ON喝水,最后回到驻地A,这位将军怎样走路程最短?
B
C
A1
A2
将军沿A-B-C-A走路程最短
考点3-2
情境导入
将军遛马---两定两动
A
图形特征:
一定两动;
基本策略:
同侧化异侧、折线化直线;
基本方法:
N个动点N条河,N次对称跑不脱;
基本原理:
两点之间线段最短.
适用模型:
将军遛马(台球两次碰壁);
【例2-2】如图,∠AOB=45 ,点P是∠AOB内一点且OP=,若点M、N分别是射线OA、OB上异于点O的动点,则△PMN周长的最小值是_____.
考点3-2
典例精讲
将军遛马---两定两动
N
M
P1
P2
P
A
O
B
N
M
2
【引例】将军每日需骑马从军营A出发,去河对岸的瞭望台B观测敌情,已知河流的宽度为30米,请问,在何地修浮桥,使每日的行程最短
考点3-3
情境导入
变态的将军饮马--- 造桥选址
A
B
a
b
A
M
N
M1
N1
M2
N2
AM1+M1N1+N1B=_____________
A N1+N1B+M1N1
AM+MN+NB=__________
A N+MN+NB
=A B+MN
A N1+N1B+M1N1____A B+MN
>
如图,MN即为所求
图形特征:
两定两动;
基本方法:
将一定点沿定长方向平移定长距离,
再用将军饮马模型解决问题;
基本原理:
两点之间线段最短.
适用模型:
造桥选址;
如图,荆州古城河在CC 处直角转弯,河宽相同,从A处到B处,须经两座桥:DD ,EE (桥宽不计),设护城河以及两座桥都是东西、南北方向的,怎样架桥可使ADD E EB的路程最短?
A
D
D
C
C
E
E
B
考点3-3
情境导入
造桥选址---两定两动(定长)
图形特征:
两定两动;
基本方法:
将一定点沿定长方向平移定长距离,
再用将军饮马模型解决问题;
基本原理:
两点之间线段最短.
适用模型:
造桥选址;
【例3-1】在矩形ABCD,AB=6,BC=8,G为AD的中点.如图,E,F为边AB上的两个动点,且EF=4,当四边形CGEF的周长最小时,则AF=____.
E
A
G
D
C
B
E
F
H
G
F
考点3-3
典例精讲
造桥选址---两定两动(定长)
5
【例3-2】如图,菱形ABCD中,AB=4,∠BAD=60 ,M,N是AC上两动点,且MN=2,则BM+BN的最小值为_____.
考点3-3
典例精讲
造桥选址---一定两动(定长)
B
A
D
C
B
N
M
M
N
2 5
知识梳理
课堂小结
将军饮马
将军饮马:这个将军饮的不是马,是数学!
解题依据:两点间线段最短;点到直线的垂直距离最短;翻折,对称.
解题策略:对称、翻折→化同为异;化异为同;化折为直.
两村一路
(同侧)和最小
B
A
B
l
A
B
l
O
P
N
M
两村一路(线段)和最小
一村两路和最小
两村两路和最小
P2
P1
A
B
M
N
O
Q
P
P
Q
B
A
Q
P
A1
A2
1.如图,正方形ABCD内接于⊙O,线段MN在对角线BD上运动,若⊙O的面积为2π,MN=1,则△AMN周长的最小值是( )
A.3 B.4 C.5 D.6
A
D
C
N
O
M
B
B
E
提升能力
强化训练
将军饮马
1.如图:已知⊙O的直径CD为2,AC的度数为60 ,点B是AC的中点,在直径CD上作出点P,使BP+AP的值最小,则BP+AP的最小值为____.
2.如图,等腰三角形ABC的底边BC长为10,面积是40,腰AC的垂直平分线EF分别交AC,AB边于E,F点,若点D为BC边的中点,点M为线段EF上一动点,则△CDM周长的最小值为____.
︵
︵
C
D
O
A
B
P
B
河边
提升能力
强化训练
将军饮马
13
M
C
F
E
B
A
D
M
2
y
O
x
A
B
3.如图,抛物线y=0.5x -4x+4与y轴交于点A,点B是OA的中点.一个动点G从点B出发,先经过x轴上的点M,再经过抛物线对称轴上的点N,然后返回到点A.如果动点G走过的路程最短为____,则点M、N的坐标为______________.
B
M
A
N
M
N
10
M(8/3,0)N(4,1)
将军遛马---两定两动
提升能力
强化训练
将军饮马
4.如图,正方形EFGH的边EF在正方形ABCD的边BC上.若AB=4,EF=2,则AG+DH的最小值为_____.
A
G
H
F
E
D
C
B
M
G
造桥选址---两定两动(定长)
提升能力
强化训练
将军饮马
2 13
5.如图,在边长为1的菱形ABCD中,∠ABC=60 ,将△ABD沿射线BD的方向平移得到△A B D ,分别连接A C,A D,B C,则A C+B C的最小值为_____.
A
D
A
D
C
B
B
A
造桥选址---一定两动(定长)
提升能力
强化训练
将军饮马
3
专题二 轴对称模型
§2.1 “将军饮马”模型
人教版中考第二轮总复习---几何模型
考点归纳
知识梳理
最值问题---解题策略
1.分析定点、动点,寻找不变特征;
2.确定路径(关键):
3.①若属于常见模型,调用模型解决问题;
②若不属于常见模型,要结合所求目标.
根据不变特征转化为基本定理或函数解决问题.
4.设计方案,求出路径长.
通过起点、终点、特殊点猜测运动路径(轨迹),
并结合不变特征进行验证;
线段最值
单动线段最值
双动线段最值
三动线段最值
1.点到点
2.点到线
3.点到圆
PA±PB
PA±kPB
费马点模型
PA+PB+PC
两点之间线段最短
垂线段最短
点心线截距最短(长).
将军饮马模型
胡不归模型
AB+BC+CD
将军饮马模型
考点归纳
知识梳理
线段最值问题---基本类型
考点3-1
视频导入
将军饮马---两定一动
草地
河流
M
N
B
【引例】如图,一位将军骑马从驻地A出发,先牵马去河边MN喝水,再回到驻地B.这位将军怎样走路程最短
考点3-1
情境导入
将军饮马---两定一动
A
P1
P2
P3
P
B'
将军沿A-P-B走路程最短.
PA+PB=_______=____.
PA+PB
AB
P1A+P1B=_______
P1A+P1B
>AB
图形特征:
两定一动;
基本策略:
同侧化异侧、折线化直线;
基本方法:
一个动点一条河,一次对称跑不脱;
基本原理:
两点之间线段最短.
适用模型:
将军饮马;
AB最短
B
A
①两点之间,线段最短;
核心知识
AC+BC>AB
B
A
C
②三角形两边之和大于第三边.
派生知识
考点3-1
模型分析
两点之间线段最短
【例1】如图,矩形ABOC的顶点A的坐标为(-4,5),D是OB的中点,E是OC上的一点,当△ADE的周长最小时,点E的坐标是( )
A.(0,) B.(0,) C.(0,2) D.(0,)
B
A
D
C
B
O
x
y
E
E
D
考点3-1
典例精讲
将军饮马---两定一动
河边
【引例1】如图,A,B均为驻地,将军某一天要从驻地A出马,先到草地边某处牧马,再到河边饮马,然后回到驻地B,这位将军怎样走路程最短?
草地
河流
P
N
M
A
将军沿A-C-D-B
走路程最短
C
D
A
B
考点3-2
情境导入
将军遛马---两定两动
图形特征:
两定两动;
基本策略:
同侧化异侧、折线化直线;
基本方法:
N个动点N条河,N次对称跑不脱;
基本原理:
两点之间线段最短.
适用模型:
将军遛马(台球两次碰壁);
【例2-1】如图,点A(a,3)B(b,1)都在双曲线y=上,点C,D分别是x轴,y轴上的动点,则四边形ABCD周长的最小值为( )
A.5 B.6 C.2+2 D.8
B
A
D
B
C
y
x
O
A'
B'
D
C
考点3-2
典例精讲
将军遛马---两定两动
河边
草地
草地
河流
N
M
O
【引例2】如图,一位将军骑马从驻地A出发,先牵马去草地OM吃草,再牵马去河边ON喝水,最后回到驻地A,这位将军怎样走路程最短?
B
C
A1
A2
将军沿A-B-C-A走路程最短
考点3-2
情境导入
将军遛马---两定两动
A
图形特征:
一定两动;
基本策略:
同侧化异侧、折线化直线;
基本方法:
N个动点N条河,N次对称跑不脱;
基本原理:
两点之间线段最短.
适用模型:
将军遛马(台球两次碰壁);
【例2-2】如图,∠AOB=45 ,点P是∠AOB内一点且OP=,若点M、N分别是射线OA、OB上异于点O的动点,则△PMN周长的最小值是_____.
考点3-2
典例精讲
将军遛马---两定两动
N
M
P1
P2
P
A
O
B
N
M
2
【引例】将军每日需骑马从军营A出发,去河对岸的瞭望台B观测敌情,已知河流的宽度为30米,请问,在何地修浮桥,使每日的行程最短
考点3-3
情境导入
变态的将军饮马--- 造桥选址
A
B
a
b
A
M
N
M1
N1
M2
N2
AM1+M1N1+N1B=_____________
A N1+N1B+M1N1
AM+MN+NB=__________
A N+MN+NB
=A B+MN
A N1+N1B+M1N1____A B+MN
>
如图,MN即为所求
图形特征:
两定两动;
基本方法:
将一定点沿定长方向平移定长距离,
再用将军饮马模型解决问题;
基本原理:
两点之间线段最短.
适用模型:
造桥选址;
如图,荆州古城河在CC 处直角转弯,河宽相同,从A处到B处,须经两座桥:DD ,EE (桥宽不计),设护城河以及两座桥都是东西、南北方向的,怎样架桥可使ADD E EB的路程最短?
A
D
D
C
C
E
E
B
考点3-3
情境导入
造桥选址---两定两动(定长)
图形特征:
两定两动;
基本方法:
将一定点沿定长方向平移定长距离,
再用将军饮马模型解决问题;
基本原理:
两点之间线段最短.
适用模型:
造桥选址;
【例3-1】在矩形ABCD,AB=6,BC=8,G为AD的中点.如图,E,F为边AB上的两个动点,且EF=4,当四边形CGEF的周长最小时,则AF=____.
E
A
G
D
C
B
E
F
H
G
F
考点3-3
典例精讲
造桥选址---两定两动(定长)
5
【例3-2】如图,菱形ABCD中,AB=4,∠BAD=60 ,M,N是AC上两动点,且MN=2,则BM+BN的最小值为_____.
考点3-3
典例精讲
造桥选址---一定两动(定长)
B
A
D
C
B
N
M
M
N
2 5
知识梳理
课堂小结
将军饮马
将军饮马:这个将军饮的不是马,是数学!
解题依据:两点间线段最短;点到直线的垂直距离最短;翻折,对称.
解题策略:对称、翻折→化同为异;化异为同;化折为直.
两村一路
(同侧)和最小
B
A
B
l
A
B
l
O
P
N
M
两村一路(线段)和最小
一村两路和最小
两村两路和最小
P2
P1
A
B
M
N
O
Q
P
P
Q
B
A
Q
P
A1
A2
1.如图,正方形ABCD内接于⊙O,线段MN在对角线BD上运动,若⊙O的面积为2π,MN=1,则△AMN周长的最小值是( )
A.3 B.4 C.5 D.6
A
D
C
N
O
M
B
B
E
提升能力
强化训练
将军饮马
1.如图:已知⊙O的直径CD为2,AC的度数为60 ,点B是AC的中点,在直径CD上作出点P,使BP+AP的值最小,则BP+AP的最小值为____.
2.如图,等腰三角形ABC的底边BC长为10,面积是40,腰AC的垂直平分线EF分别交AC,AB边于E,F点,若点D为BC边的中点,点M为线段EF上一动点,则△CDM周长的最小值为____.
︵
︵
C
D
O
A
B
P
B
河边
提升能力
强化训练
将军饮马
13
M
C
F
E
B
A
D
M
2
y
O
x
A
B
3.如图,抛物线y=0.5x -4x+4与y轴交于点A,点B是OA的中点.一个动点G从点B出发,先经过x轴上的点M,再经过抛物线对称轴上的点N,然后返回到点A.如果动点G走过的路程最短为____,则点M、N的坐标为______________.
B
M
A
N
M
N
10
M(8/3,0)N(4,1)
将军遛马---两定两动
提升能力
强化训练
将军饮马
4.如图,正方形EFGH的边EF在正方形ABCD的边BC上.若AB=4,EF=2,则AG+DH的最小值为_____.
A
G
H
F
E
D
C
B
M
G
造桥选址---两定两动(定长)
提升能力
强化训练
将军饮马
2 13
5.如图,在边长为1的菱形ABCD中,∠ABC=60 ,将△ABD沿射线BD的方向平移得到△A B D ,分别连接A C,A D,B C,则A C+B C的最小值为_____.
A
D
A
D
C
B
B
A
造桥选址---一定两动(定长)
提升能力
强化训练
将军饮马
3
同课章节目录
