专题4.1圆---隐圆模型 课件(共23张PPT)-中考数学二轮复习必会几何模型剖析(全国通用)
文档属性
| 名称 | 专题4.1圆---隐圆模型 课件(共23张PPT)-中考数学二轮复习必会几何模型剖析(全国通用) |  | |
| 格式 | pptx | ||
| 文件大小 | 5.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-25 07:04:31 | ||
图片预览




文档简介
(共23张PPT)
专题四 与圆有关的模型
§4.1 “隐圆”模型
人教版中考第二轮总复习---几何模型
考点3-1
知识归纳
定点定长型
模型分析
图形 条件
结论
原理
特征
O
B
C
A
OA=OB=OC
A、B、C,在以O为圆心,OA为半径的圆上.
到定点的距离等于定长的点的集合是以定点为圆心定长为半径的圆;
有几个点到同一个点的距离相等时,要想到构造圆.
考点3-1
典例精讲
定点定长型
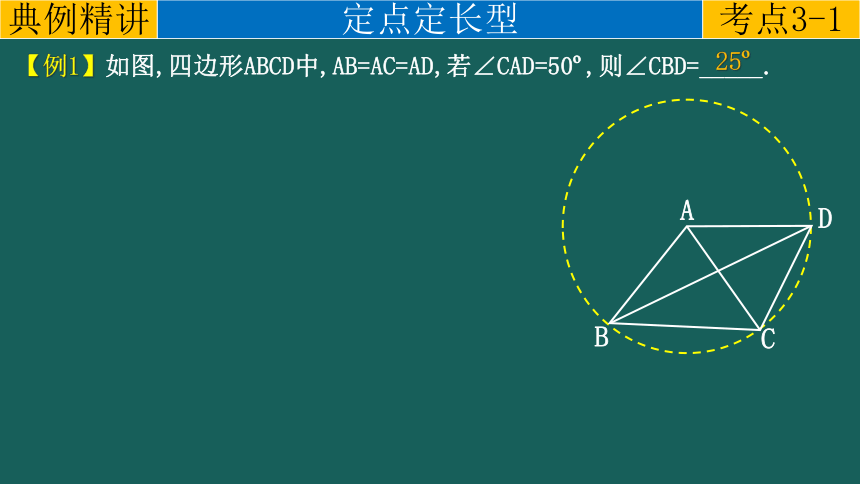
【例1】如图,四边形ABCD中,AB=AC=AD,若∠CAD=50 ,则∠CBD=_____.
25
B
C
D
A
考点3-1
针对训练
定点定长型
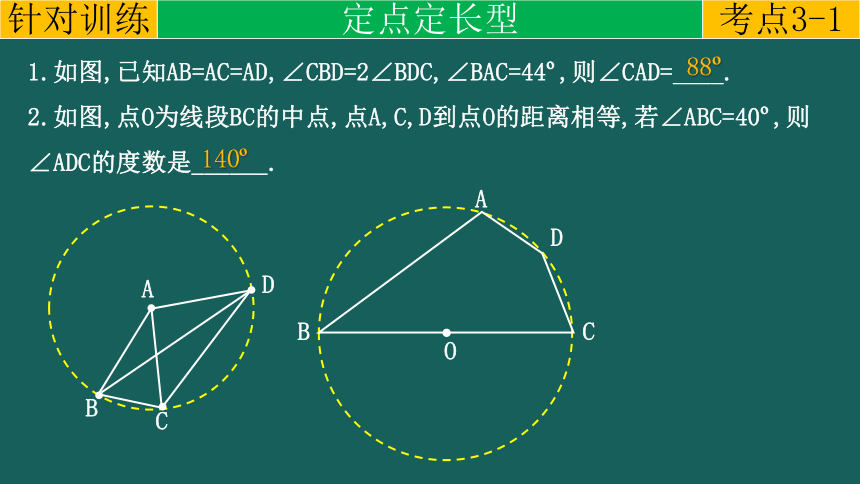
1.如图,已知AB=AC=AD,∠CBD=2∠BDC,∠BAC=44 ,则∠CAD=____.
2.如图,点O为线段BC的中点,点A,C,D到点O的距离相等,若∠ABC=40 ,则∠ADC的度数是______.
88
A
C
D
B
B
O
C
D
A
140
考点3-2
知识归纳
定边对定角
模型分析
图形 条件
结论
原理
备注
图①
A
P1
B
P2
P3
O
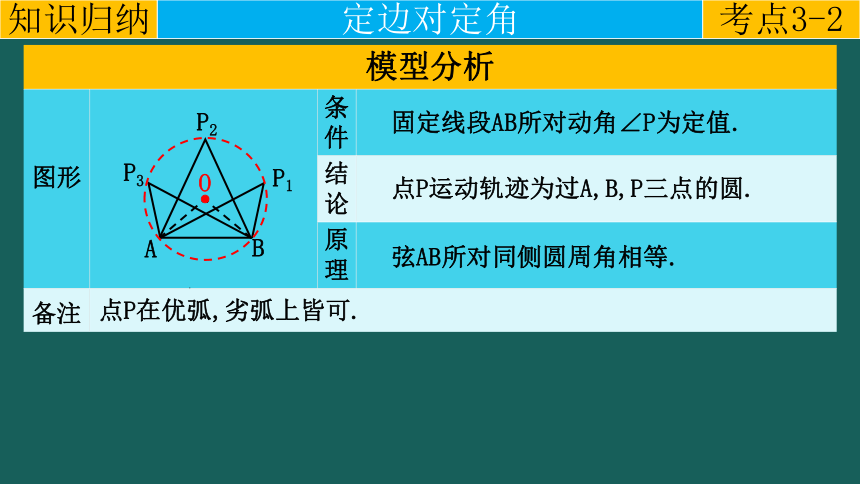
弦AB所对同侧圆周角相等.
固定线段AB所对动角∠P为定值.
点P在优弧,劣弧上皆可.
点P运动轨迹为过A,B,P三点的圆.
考点3-2
典例精讲
定边对定角
【例2-1】如图,AC为边长为4的菱形ABCD的对角线,∠ABC=60 .点M和N分别从点B、C同时出发,以相同的速度沿BC、CA运动.连接AM和BN,交于点P,则PC长的最小值为____.
4 3
3
B
P
N
M
A
D
C
考点3-2
知识归纳
定边对定角---直径对直角
模型分析
图形 条件
结论
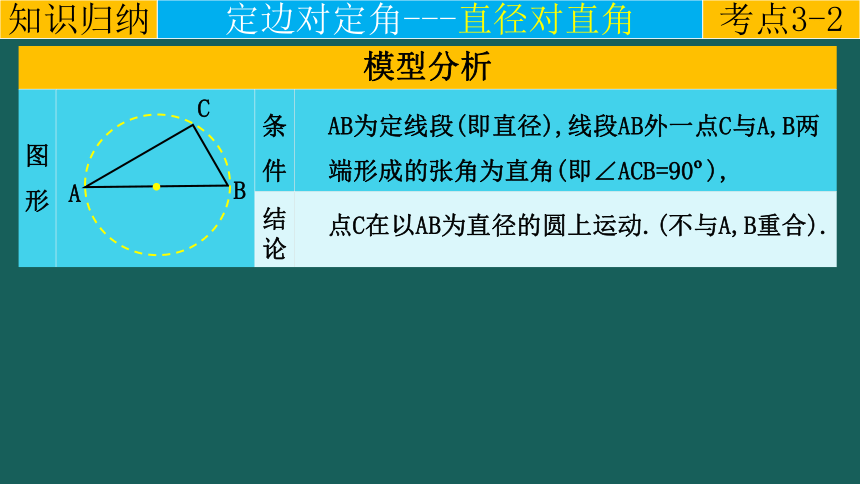
AB为定线段(即直径),线段AB外一点C与A,B两端形成的张角为直角(即∠ACB=90 ),
A
C
B
点C在以AB为直径的圆上运动.(不与A,B重合).
考点3-2
典例精讲
定边对定角---直径对直角
【例2-2】在正方形ABCD中,AD=2,E,F分别为边DC,CB上的点,且始终保持DE=CF,连接AE和DF交于点P,则线段CP的最小值为_____.
A
P
F
C
E
D
B
Q
5-1
考点3-3
知识归纳
四点共圆
模型分析
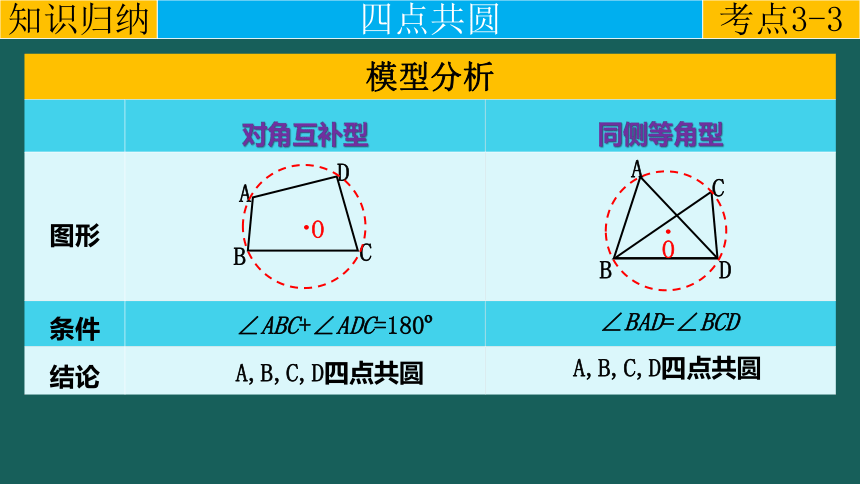
对角互补型 同侧等角型
图形
条件
结论
A
B
D
C
A
B
D
C
O
O
∠ABC+∠ADC=180
A,B,C,D四点共圆
∠BAD=∠BCD
A,B,C,D四点共圆
考点3-3
典例精讲
四点共圆
【例3】如图,在四边形ABCD中,∠B=60 ,∠D=120 ,BC=CD=a,
则AB-AD=____.
E
120
D
C
B
A
60
120
a
a
a
a
1.如图,已知∠ABC=∠ADC=90 ,∠DAB=45 ,M,N分别是AC、BD的中点.若AC=10,则MN=____.
5 2
2
A
M
N
C
D
B
考点3-3
针对训练
四点共圆
1.如图,在四边形ABCD中,∠ABC=∠ADC=90 ,E为对角线AC的中点,连接BE,ED,BD.若∠BAD=58 ,则∠EBD的度数为_____度.
32
A
E
D
C
B
四点共圆-对角互补
考点3-3
针对训练
四点共圆
2.如图,△ABD,△AEC都是等腰三角形,AB=AD,AE=AC,AC>AB
∠BAD=∠EAC=α,连接CD,BE交于点P,连接AP.
(1)求∠BPD的度数(用含α的代数式表示);
(2)求证:∠APD=∠ABD.
(3)PA平分∠DPE.
F
E
A
P
C
E
B
D
(3)①利用全等三角形对应边上的高相等得OE=OF;
②在利用到角的两边距离相等的点在这个角的平分线上.
(1)(2)利用四点共圆求解
23.在△AOB中,∠AOB=90 ,AO=BO=2,D为AO的中点,以O为圆心,DO为半径,作扇形COD,∠COD=90 ,将扇形COD绕点O顺时针旋转α(0 <α<360 ).
(1)在旋转过程中,BD的最小值为_____;
(2)当α=30 ,试判断BD与CD的位置关系,并给予证明;
(3)当C、D、B在同一直线上时,求BC的长。
⌒
A
D
C
B
O
2
A
D
C
B
O
E
A
B
O
D
C
D
C
D
C
3.如图,在△ABC中,AB=AC,∠BAC<90 ,点M,N分别为边AB,BC的中点,连接MN,将△BMN绕点B顺时针旋转α,得到△BEF,连接AE,CF.当旋转角α满足0 <α<360 ,点C,E,F在同一直线上时,证明点A,B,C,E四点共圆,并利用所提供的备用图探究∠BAE与∠ABF的数量关系,并说明理由.
A
N
M
C
B
A
N
M
C
B
备用图
E
F
E
F
考点3-3
针对训练
四点共圆
1.如图,∠AOB=45 ,边OA、OB上分别有两个动点C、D,连接CD,以CD为 直角边作等腰Rt△CDE,且CD=CE,当CD长保持不变且等于2cm时,则OE长的最大值为________cm.
2.如图,已知在Rt△ABC中,AC=5,BC=12,∠ACB=90 ,P是边AB上的动点,Q是边BC上的动点,且∠CPQ=90 ,求线段CQ的取值范围____________.
3.如图,在四边形ABCD中,AD∥BC,BD⊥DC,若AD=2,BC=4,则四边形ABCD面积的最大值是___.
10+ 2
A
B
D
O
C
E
20
3
≤CQ≤12
6
A
P
B
Q
O
C
B
A
D
C
提升能力
强化训练
“隐圆”模型
提升能力
强化训练
“隐圆”模型
1.已知P为△ABC内一点,且PA=PB=PC=a.若AB=3,∠C=45 ,则a=______.
2.如图,在△ABC中,∠ACB=90 ,O是AB的中点,将OB绕点O顺时针旋转α(0 <α<180 )得到OP,连接AP.若∠BAC=20 ,当△ACP为等腰三角形时,α的值为________________.
P
C
B
A
3 2
2
40 或70 或100
A
O
P
B
C
提升能力
强化训练
“隐圆”模型
3.如图,在正△ABC中,AB=2,若P为△ABC内一动点,且满足∠APC=150 ,则线段PB长度的最小值为_______.
4.如图,Rt△ABC中,AB⊥BC,AB=6,BC=4,P是△ABC内部的一个动点,且AP⊥BP,则线段CP长的最小值为____.
B
P
C
A
O
P
A
C
B
P
O
2
定边对定角
定边对直角
2 3-2
提升能力
强化训练
“隐圆”模型
5.点P在在等腰三角形ABC的外部,且AP=AB=AC,∠A=72 ,那么∠BPC的度数为__________.
6.如图,四边形ABCD中,AB=AC=AD=2,BC=1,AB∥CD,则BD=____.
36 或144
A
C
B
P1
P2
B
D
C
A
E
定点定长型
定点定长型
15
提升能力
强化训练
“隐圆”模型
7.如图,在△ABC中,AD⊥BC于D,DE⊥AB于E,DF⊥AC于F,连接EF.
求证:∠AEF=∠C.
A
E
F
C
D
B
利用AEDF四点共圆证明∠1=∠2
∵∠2+∠3=90 ,∠B+∠3=90 .
∴∠1=∠B
又∵∠BAC=∠BAC
∴∠AEF=∠C
1
3
2
四点共圆-对角互补
提升能力
强化训练
“隐圆”模型
8.如图,E是正方形ABCD的边BC反向延长线上的一点,∠AEF=90 ,且EF交正方形外角的平分线CM的反向延长线于点F.求证:AE=EF.
A
N
M
F
E
C
B
D
方法一:延长AB至G,使BG=BE,连接EG,
证△AEG≌△EFG得AE=EF.
方法二:连接AC,AF,得∠ACF=∠AEF=90 ,
∴A、E、F、C四点共圆.
G
∴∠EAF=∠ECF=45
∴∠EAF=∠EFA=45
∴AE=EF
四点共圆-对角互补
提升能力
强化训练
“隐圆”模型
9.如图,E,F是正方形ABCD的边AD上两个动点,满足AE=DF.连接CF交BD于点G,连接BE交AG于点H.若正方形的边长为2,则线段DH长度的最小值是_____.
A
D
C
B
F
E
G
H
H
O
E
F
G
【分析】根据条件可知:∠DAG=∠DCG=∠ABE,
易证AG⊥BE,即∠AHB=90 ,
∴点H的轨迹是以AB为直径的圆弧,
当D、H、O共线时,DH取到最小值,
由勾股定理可求DH最小=
定边对直角
5-1
5-1
提升能力
强化训练
“隐圆”模型
23.如图,在∠ABC=90 ,BA=BC.将线段AB绕点A逆时针旋转90 得到线段DA,E是边BC上的一动点,连接DE交AC于点F,连接BF.
(1)求证:FB=FD;
(2)如图2,连结CD,点H在线段BE上(不含端点),且BH=CE,连结AH交BF于点N.
①判断AH与BF的位置关系,并证明你的结论;
②连接CN.若AB=2,请直接写出线段CN长度的最小值.
H
N
A
F
E
C
D
B
O
专题四 与圆有关的模型
§4.1 “隐圆”模型
人教版中考第二轮总复习---几何模型
考点3-1
知识归纳
定点定长型
模型分析
图形 条件
结论
原理
特征
O
B
C
A
OA=OB=OC
A、B、C,在以O为圆心,OA为半径的圆上.
到定点的距离等于定长的点的集合是以定点为圆心定长为半径的圆;
有几个点到同一个点的距离相等时,要想到构造圆.
考点3-1
典例精讲
定点定长型
【例1】如图,四边形ABCD中,AB=AC=AD,若∠CAD=50 ,则∠CBD=_____.
25
B
C
D
A
考点3-1
针对训练
定点定长型
1.如图,已知AB=AC=AD,∠CBD=2∠BDC,∠BAC=44 ,则∠CAD=____.
2.如图,点O为线段BC的中点,点A,C,D到点O的距离相等,若∠ABC=40 ,则∠ADC的度数是______.
88
A
C
D
B
B
O
C
D
A
140
考点3-2
知识归纳
定边对定角
模型分析
图形 条件
结论
原理
备注
图①
A
P1
B
P2
P3
O
弦AB所对同侧圆周角相等.
固定线段AB所对动角∠P为定值.
点P在优弧,劣弧上皆可.
点P运动轨迹为过A,B,P三点的圆.
考点3-2
典例精讲
定边对定角
【例2-1】如图,AC为边长为4的菱形ABCD的对角线,∠ABC=60 .点M和N分别从点B、C同时出发,以相同的速度沿BC、CA运动.连接AM和BN,交于点P,则PC长的最小值为____.
4 3
3
B
P
N
M
A
D
C
考点3-2
知识归纳
定边对定角---直径对直角
模型分析
图形 条件
结论
AB为定线段(即直径),线段AB外一点C与A,B两端形成的张角为直角(即∠ACB=90 ),
A
C
B
点C在以AB为直径的圆上运动.(不与A,B重合).
考点3-2
典例精讲
定边对定角---直径对直角
【例2-2】在正方形ABCD中,AD=2,E,F分别为边DC,CB上的点,且始终保持DE=CF,连接AE和DF交于点P,则线段CP的最小值为_____.
A
P
F
C
E
D
B
Q
5-1
考点3-3
知识归纳
四点共圆
模型分析
对角互补型 同侧等角型
图形
条件
结论
A
B
D
C
A
B
D
C
O
O
∠ABC+∠ADC=180
A,B,C,D四点共圆
∠BAD=∠BCD
A,B,C,D四点共圆
考点3-3
典例精讲
四点共圆
【例3】如图,在四边形ABCD中,∠B=60 ,∠D=120 ,BC=CD=a,
则AB-AD=____.
E
120
D
C
B
A
60
120
a
a
a
a
1.如图,已知∠ABC=∠ADC=90 ,∠DAB=45 ,M,N分别是AC、BD的中点.若AC=10,则MN=____.
5 2
2
A
M
N
C
D
B
考点3-3
针对训练
四点共圆
1.如图,在四边形ABCD中,∠ABC=∠ADC=90 ,E为对角线AC的中点,连接BE,ED,BD.若∠BAD=58 ,则∠EBD的度数为_____度.
32
A
E
D
C
B
四点共圆-对角互补
考点3-3
针对训练
四点共圆
2.如图,△ABD,△AEC都是等腰三角形,AB=AD,AE=AC,AC>AB
∠BAD=∠EAC=α,连接CD,BE交于点P,连接AP.
(1)求∠BPD的度数(用含α的代数式表示);
(2)求证:∠APD=∠ABD.
(3)PA平分∠DPE.
F
E
A
P
C
E
B
D
(3)①利用全等三角形对应边上的高相等得OE=OF;
②在利用到角的两边距离相等的点在这个角的平分线上.
(1)(2)利用四点共圆求解
23.在△AOB中,∠AOB=90 ,AO=BO=2,D为AO的中点,以O为圆心,DO为半径,作扇形COD,∠COD=90 ,将扇形COD绕点O顺时针旋转α(0 <α<360 ).
(1)在旋转过程中,BD的最小值为_____;
(2)当α=30 ,试判断BD与CD的位置关系,并给予证明;
(3)当C、D、B在同一直线上时,求BC的长。
⌒
A
D
C
B
O
2
A
D
C
B
O
E
A
B
O
D
C
D
C
D
C
3.如图,在△ABC中,AB=AC,∠BAC<90 ,点M,N分别为边AB,BC的中点,连接MN,将△BMN绕点B顺时针旋转α,得到△BEF,连接AE,CF.当旋转角α满足0 <α<360 ,点C,E,F在同一直线上时,证明点A,B,C,E四点共圆,并利用所提供的备用图探究∠BAE与∠ABF的数量关系,并说明理由.
A
N
M
C
B
A
N
M
C
B
备用图
E
F
E
F
考点3-3
针对训练
四点共圆
1.如图,∠AOB=45 ,边OA、OB上分别有两个动点C、D,连接CD,以CD为 直角边作等腰Rt△CDE,且CD=CE,当CD长保持不变且等于2cm时,则OE长的最大值为________cm.
2.如图,已知在Rt△ABC中,AC=5,BC=12,∠ACB=90 ,P是边AB上的动点,Q是边BC上的动点,且∠CPQ=90 ,求线段CQ的取值范围____________.
3.如图,在四边形ABCD中,AD∥BC,BD⊥DC,若AD=2,BC=4,则四边形ABCD面积的最大值是___.
10+ 2
A
B
D
O
C
E
20
3
≤CQ≤12
6
A
P
B
Q
O
C
B
A
D
C
提升能力
强化训练
“隐圆”模型
提升能力
强化训练
“隐圆”模型
1.已知P为△ABC内一点,且PA=PB=PC=a.若AB=3,∠C=45 ,则a=______.
2.如图,在△ABC中,∠ACB=90 ,O是AB的中点,将OB绕点O顺时针旋转α(0 <α<180 )得到OP,连接AP.若∠BAC=20 ,当△ACP为等腰三角形时,α的值为________________.
P
C
B
A
3 2
2
40 或70 或100
A
O
P
B
C
提升能力
强化训练
“隐圆”模型
3.如图,在正△ABC中,AB=2,若P为△ABC内一动点,且满足∠APC=150 ,则线段PB长度的最小值为_______.
4.如图,Rt△ABC中,AB⊥BC,AB=6,BC=4,P是△ABC内部的一个动点,且AP⊥BP,则线段CP长的最小值为____.
B
P
C
A
O
P
A
C
B
P
O
2
定边对定角
定边对直角
2 3-2
提升能力
强化训练
“隐圆”模型
5.点P在在等腰三角形ABC的外部,且AP=AB=AC,∠A=72 ,那么∠BPC的度数为__________.
6.如图,四边形ABCD中,AB=AC=AD=2,BC=1,AB∥CD,则BD=____.
36 或144
A
C
B
P1
P2
B
D
C
A
E
定点定长型
定点定长型
15
提升能力
强化训练
“隐圆”模型
7.如图,在△ABC中,AD⊥BC于D,DE⊥AB于E,DF⊥AC于F,连接EF.
求证:∠AEF=∠C.
A
E
F
C
D
B
利用AEDF四点共圆证明∠1=∠2
∵∠2+∠3=90 ,∠B+∠3=90 .
∴∠1=∠B
又∵∠BAC=∠BAC
∴∠AEF=∠C
1
3
2
四点共圆-对角互补
提升能力
强化训练
“隐圆”模型
8.如图,E是正方形ABCD的边BC反向延长线上的一点,∠AEF=90 ,且EF交正方形外角的平分线CM的反向延长线于点F.求证:AE=EF.
A
N
M
F
E
C
B
D
方法一:延长AB至G,使BG=BE,连接EG,
证△AEG≌△EFG得AE=EF.
方法二:连接AC,AF,得∠ACF=∠AEF=90 ,
∴A、E、F、C四点共圆.
G
∴∠EAF=∠ECF=45
∴∠EAF=∠EFA=45
∴AE=EF
四点共圆-对角互补
提升能力
强化训练
“隐圆”模型
9.如图,E,F是正方形ABCD的边AD上两个动点,满足AE=DF.连接CF交BD于点G,连接BE交AG于点H.若正方形的边长为2,则线段DH长度的最小值是_____.
A
D
C
B
F
E
G
H
H
O
E
F
G
【分析】根据条件可知:∠DAG=∠DCG=∠ABE,
易证AG⊥BE,即∠AHB=90 ,
∴点H的轨迹是以AB为直径的圆弧,
当D、H、O共线时,DH取到最小值,
由勾股定理可求DH最小=
定边对直角
5-1
5-1
提升能力
强化训练
“隐圆”模型
23.如图,在∠ABC=90 ,BA=BC.将线段AB绕点A逆时针旋转90 得到线段DA,E是边BC上的一动点,连接DE交AC于点F,连接BF.
(1)求证:FB=FD;
(2)如图2,连结CD,点H在线段BE上(不含端点),且BH=CE,连结AH交BF于点N.
①判断AH与BF的位置关系,并证明你的结论;
②连接CN.若AB=2,请直接写出线段CN长度的最小值.
H
N
A
F
E
C
D
B
O
同课章节目录
