专题4.2圆---利用“隐圆”模型求最值-中考数学二轮复习必会几何模型剖析(全国通用)
文档属性
| 名称 | 专题4.2圆---利用“隐圆”模型求最值-中考数学二轮复习必会几何模型剖析(全国通用) |  | |
| 格式 | pptx | ||
| 文件大小 | 6.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-25 09:47:59 | ||
图片预览





文档简介
(共26张PPT)
专题四 与圆有关的模型
人教版中考第二轮总复习---几何模型
§4.2 利用“隐圆”模型求最值
考点归纳
知识梳理
“隐圆”模型概述
在辅助圆问题中,我们了解了求关于动点最值问题的方式之一---求出动点轨迹,即可求出关于动点的最值.
本节课我们继续讨论另一类动点引发的最值问题,在此类题目中,题目或许先描述的是动点P,但最终问题问的可以是另一点Q,当然P、Q之间存在某种联系,从P点出发探讨Q点运动轨迹并求出最值,为常规思路.
近几年中考数学,有一些高频考题,如线段最值问题,动点路程问题,除了填空选择关于圆的计算以及解答题关于圆的证明以外,常常会以压轴题的形式考察圆的重要性质.在这些题目的图形中往往没有出现“圆”,但在解题时却要用到“圆”的知识点,我们把这种类型的题目称之为“隐圆模型”.
考点4-1
模型分析
点圆最值---点心线
O
P
点P在⊙O外
B
A
O
P
点P在⊙O内
B
A
C
PA=PO-AO=PO-CO<PC.
PB=PO+BO=PO+CO>PC.
∴PA最短
∴PB最长
C
PA=AO-PO=CO-PO<PC.
PB=PO+BO=PO+CO>PC.
∴PA最短
∴PB最长
点圆之间,点心线截距最短(长)
考点4-1
典型例题
点圆最值---点心线
【例1】有一架靠在直角墙面的梯子(MN=4)正在下滑,D点出有一只猫紧紧盯住位于梯子MN的正中间E处的老鼠,等待与老鼠距离最小时扑捉.把墙面,梯子,猫和老鼠看成同一平面内的线或点,点D到BA,BC的距离分别为4和2.猫与老鼠的距离DE的最小值为_______.
N
A
D
E
M
C
B
2 5-2
考点4-1
针对训练
点圆最值---点心线
1.如图,⊙O、⊙C,OC=5,点A、B分别是平面内的动点,且OA=4,BC=3,则OB长的最大值为______,OB长的最小值为______,AC长的最大值为_____,AC长的最小值为______,AB长的最大值为______,AB长的最小值为____.
2.如图,在矩形ABCD中,AB=4,AD=6,点E是AB边上的中点,点F是线段BC边上的动点,将△EBF沿EF所在直线折叠得到△EB F,连接B C,则B C最小值是________.
1
8
2
9
12
0
O
C
A
B
B
E
F
C
D
B
B
2 10-2
A
AB为⊙O的一条定弦,点C为圆上一动点,当点C在何处,△ABC的面积最大.
考点4-2
模型分析
线圆最值---心垂线
当CH⊥AB且CH的延长线过圆心O时,线段CH即为点C到弦AB的最大距离,此时△ABC的面积最大.
C
H
若点C在优弧AB上
O
B
A
C
当CH⊥AB且CH过圆心O时,线段CH即为点C到弦AB的最大距离,此时△ABC的面积最大;
O
C
B
A
H
若点C在劣弧AB上
考点4-2
典例精讲
线圆最值---心垂线
【例2-1】在△ABC中,AB=4,∠C=60 ,∠A≥∠B,则BC的长的取值范围是___________,△ABC面积的最大值为____.
C
C
A
B
60
4
O
C
4≤BC≤
8 3
3
4 3
考点4-2
模型分析
线圆最值---心垂线
O
l
如图,⊙O与直线l相离,点P是⊙O上的一个动点,设圆心O到直线l的距离为d,⊙O的半径为r,则点P到直线l的最小距离是____,点P到直线l的最大距离是_____.
d-r
d+r
A
B
P
H
M
∵OP+PM>OM>OH=OB+BH,OB=OP.
∵AH=OA+OH=OP+OH>PH>PM,
①线圆之间,心垂线截距最短(长).
结论:AH最长,BH最短.
∴PM>BH.
∴AH>PM.
考点4-2
典例精讲
线圆最值---心垂线
【例2-2】如图,在Rt△ABC中,∠C=90 ,AC=6,BC=8,点F在边AC上,并且CF=1,点E为边BC上的动点,△CEF沿直线EF翻折,点C落在点P处,则点P到边AB距离的最小值是_____.
P
P
H
E
A
F
C
B
E
1.2
考点4-3
模型分析
圆中最长弦---直径
1.定圆中最长的弦是直径;
O
B
A
D
C
2.定弦中最小的圆是以该弦为直径的圆
A
B
O
B
A
3.经过圆中定点最短的弦是垂直于过这点直径的弦;
O
P
C
D
E
F
H
考点4-3
典例精讲
圆中最长弦---直径
【例3-1】在△ABC中,∠ACB=90 ,AC=6,BC=8,O为AB的中点,过O作OE⊥OF,OE,OF分别交射线AC,BC于E,F,则EF的最小值为____.
【简答】∵∠EOF=∠C=90 ,
B
O
A
C
E
F
F
E
5
∴C,O均在以EF为直径的圆上.
∵EF是圆的直径,O、C均在圆上,且OC长度固定,要使EF最短,则圆最小,要使圆最小,由于OC为固定长度,则OC为直径时,圆最小,此时EF=CO=OA=OB=5(斜边上中线等于斜边一半)
考点4-3
典例精讲
圆中最长弦---直径
【例3-2】如图,P为⊙O内的一个定点,A为⊙O上的一个动点,射线AP,AO分别与⊙O交于点B,C.若⊙O的半径为3,OP=,则弦BC长的最大值为( )
A.2 B.3 C. D.3
A
C
A
B
P
O
A
C
B
考点4-4
模型分析
定角夹定高
【题型背景】在一些最值问题中,给定一个角,并且过定角的顶点作对边的垂线为定值时,也存在最值问题,面对这种问题我们借助“隐圆”进行说明:我们称这种问题为:“定角夹定高”模型也称“探照灯”模型.主要解决:
(1)线段最短问题; (2)面积最小问题.
【模型】如右图所示,在△ABC中,∠BAC=α为定值,AD为BC边上的高,且AD=h为定值,则底边BC存在最小值,△ABC的面积存在最小值.
A
h
D
C
B
α
O
α
E
【突破点】1.找出“隐圆”---三角形外接圆;
2.定高过外心(半径+弦心距)≥定高.
证明:作△ABC的外接圆,圆心为O,连接AO,BO,CO,
作OE⊥BC于点E.易得∠BOE=α,则OE=r·cosα.
∵OA+OE≥AD,
∴r+r·cosα≥h.
∴r≥
h
1+cosα
∴BE=r·sinα≥
h·sinα
1+cosα
∴BC=2BE≥
2h·sinα
1+cosα
∴S△ABCmin=
h2·sinα
1+cosα
考点4-4
典例精讲
定角夹定高
【例3-1】如图,在△ABC中,∠BAC=60 ,BC边上的高AD为3,则BC的最小值为___.
O
60
E
A
D
C
B
60
解:作△ABC的外接圆,连接OA,OB,OC,
设半径为r,
则∠BOC=2∠A=2×60=120
∵OB=OC.
∴∠BOE=60 .
∴OE=0.5r.
由垂线段最短可知:
OA+OE≥AD
作OE⊥BC于点E.
6
O
A
C
B
D
BC=2BE=
3r.
即:r+ r≥
1
2
3 3
解得:r≥
2 3
∴BC最小= =6.
3r
考点4-4
典例精讲
定角夹定高
【例3-2】(2022 T23)【拓展应用】将任意一个锐角的顶点放在正方形中心O处,该锐角记为∠GOH(设∠GOH=α),将∠GOH绕点O逆时针旋转,在旋转过程中,∠GOH的两边与正方形ABCD的边所围成的图形的面积为S2,请直接写出S2的最小值与最大值(分别用含α的式子表示).
A
O
C
D
B
G
N
M
H
Q
(F)
提升能力
强化训练
与“圆”有关的最值问题
1.如图,在矩形ABCD中,AB=3,BC=4,O为矩形ABCD的中心,以D为圆心,1为半径作⊙D,P为⊙D上的一个动点,连接AP,OP,AO,则△AOP面积的最大值为_______.
2.如图,在边长为2的菱形ABCD中,∠A=60 ,M是AD边的中点,N是AB上一个动点,将△AMN沿MN所在直线翻折得到△A MN,连接A C,则A C长的最小值为______.
17
4
A
P
O
D
C
B
7-1
A
A
N
M
D
C
B
提升能力
强化训练
与“圆”有关的最值问题
3.如图,在矩形ABCD中,AB=60,AD=45,P,Q分别是AB,AD边上的动点,PQ=52,以PQ为直径的⊙O与BD交于点M,N,则MN的最大值为_____.
A
B
C
D
Q
P
M
N
O
H
O
N
M
Q
P
∵MN=2NH=
∴当OH最短时,MN最长.
48
ON2-OH2
= 262-OH2
提升能力
强化训练
与“圆”有关的最值问题
4.如图,在Rt△ABC中,∠C=90 ,BC=6,AC=8,D,E分别是BC,AC上的一点,且DE=6.若以DE为直径的圆与斜边AB相交于M,N两点,则MN的最大值为_____. 5.如图,在⊙O中,直径AB=12,点D是圆上任意一点(A,B除外),P为CD的中点,过点D作DE⊥AB于点E,连接AD,EP.则EP的最大值为____.
24/5
A
O
M
D
E
C
B
N
A
C
D
O
E
B
P
F
6
提升能力
强化训练
与“圆”有关的最值问题
6.如图,AB是⊙O的弦,点C是ACB上的动点(C不与A,B重合),CH⊥AB,垂足为H,点M是BC的中点.若⊙O的半径是3,则MH长的最大值是_____.
7.如图,Rt△AOB∽Rt△DOC,∠AOB=∠COD=90 ,M为OA的中点,OA=5,OB=12.将△COD绕点O旋转,连接AD,CB,并延长交于点P,连接MP,则MP的最大值为_____.
3
︵
12.5
O
B
A
H
M
C
C
(M)
(H)
O
M
D
P
B
A
C
I
N
提升能力
强化训练
与“圆”有关的最值问题
10.如图,等边△ABC中,AB=6,P为AB上一动点,PD⊥BC,PE⊥AC,
(1)求∠DPE的度数;(2)求DE的最小值.
【简答】∵∠PEC=∠PDC=90 ,故四边形PDCE对角互补,故PDCE四点共圆,如图.
∠EOD=2∠ECD=120 ,要使得DE最小,则要使圆的半径最小,故直径PC最小,当CP⊥AB时,PC最短为 ,则可求出DE=4.5.
D
E
P
A
C
B
O
3 3
提升能力
强化训练
与“圆”有关的最值问题
11.如图,AC是半径为1的⊙的一条弦,点D是⊙O直径AB延长线上一点,AC=CD,BC=BD.(1)求证:直线CD是⊙O的切线;
(2)点P在弧AEB上运动,过点C作CP的垂线,与PA的延长线交于点F.
①当点P运动到与点C关于直径AB对称时,求PF的长;
②当点P运动到何处,PF取最大值 请直接写出此时点P的位置以及PF的长.
A
O
B
D
C
PF=2PC=2×2=4
PF=2PC=2 3
提升能力
强化训练
与“圆”有关的最值问题
4.点E在边长为4的正方形ABCD的边BC上,点F在边CD上,∠EAF=45 ,则△AEF面积的最小值为_________.
A
F
C
D
E
B
F
O
H
定角夹定高
16 2-16
提升能力
强化训练
与“圆”有关的最值问题
5.如图,半径为2cm,圆心角为90 的扇形OAB的弧AB上有一动点P,从点P向半径OA引垂线PH交OA于点H,设△OPH的内心为I,当点P在弧AB上从点A运动到点B时,内心I所经过的路径长为_____.
C
P
H
I
A
B
O
分析:连接AI,由内心的性质可得∠PIO=135 ,
定角夹定高
2π
2
90π 2
180
=
2
2
π
∵OI平分∠AOP,OP=OA,
∴△AIO≌△PIO,
∴∠AIO=∠PIO=135 ,
∵OA为定边,∠AIO=135 为定角.
∴P在以OA为弦且圆心角为90 的⊙C上运动.
由弧长公式可求得内心I的运动路径长为:
易求AC= 2.
提升能力
强化训练
与“圆”有关的最值问题
6.如图,已知以AB为直径的⊙O,C为弧AB的中点,P为弧BC上任意一点,CD⊥CP交AP于D,连接BD,若AB=6,则BD的最小值为_______.
G
A
P
C
O
B
D
分析:连接AC,易得∠P=45 ,
∴△CDP为等腰三角形,
∴∠ADC=135 为定角,AC为定边.
∴∠AGC=90 ,
∵AB=6,∴ ,∴AG=CG=3.
定角夹定高
3 5-3
提升能力
强化训练
与“圆”有关的最值问题
9.如图,在四边形ABCD中,AB=AD=CD=4,AD∥BC,∠B=60 ,点E、F分别为边BC、CD上两个动点,且∠EAF=60 ,则△AEF的面积是否存在最小值 若存在,求出其最小值;若不存在,请说明理由.
【简答】将△ADF绕点A顺时针旋转120 ,得△ABF ,则∠EAF =60 ,易证△AEF ≌△AEF,作△AEF 的外接圆⊙O,作OH⊥BC于点H,AG⊥BC于点G,则∠F OH=60 ,设⊙O的半径为r,则OH=0.5OF=0.5r.∵OA+OH≥AG,
A
E
C
F
D
B
O
G
H
F
定角夹定高
提升能力
强化训练
与“圆”有关的最值问题
A
C
D
F
E
B
C
B
F
E
45
F
O
45
H
10.在四边形ABCD中,∠BAD=45 ,∠B=∠D=90 ,CB=CD=,点E、F分别为AB、AD上的点,若保持CE⊥CF,那么四边形AECF的面积是否存在最大值,若存在,求出面积的最大值;若不存在,请说明理由.
定角夹定高
专题四 与圆有关的模型
人教版中考第二轮总复习---几何模型
§4.2 利用“隐圆”模型求最值
考点归纳
知识梳理
“隐圆”模型概述
在辅助圆问题中,我们了解了求关于动点最值问题的方式之一---求出动点轨迹,即可求出关于动点的最值.
本节课我们继续讨论另一类动点引发的最值问题,在此类题目中,题目或许先描述的是动点P,但最终问题问的可以是另一点Q,当然P、Q之间存在某种联系,从P点出发探讨Q点运动轨迹并求出最值,为常规思路.
近几年中考数学,有一些高频考题,如线段最值问题,动点路程问题,除了填空选择关于圆的计算以及解答题关于圆的证明以外,常常会以压轴题的形式考察圆的重要性质.在这些题目的图形中往往没有出现“圆”,但在解题时却要用到“圆”的知识点,我们把这种类型的题目称之为“隐圆模型”.
考点4-1
模型分析
点圆最值---点心线
O
P
点P在⊙O外
B
A
O
P
点P在⊙O内
B
A
C
PA=PO-AO=PO-CO<PC.
PB=PO+BO=PO+CO>PC.
∴PA最短
∴PB最长
C
PA=AO-PO=CO-PO<PC.
PB=PO+BO=PO+CO>PC.
∴PA最短
∴PB最长
点圆之间,点心线截距最短(长)
考点4-1
典型例题
点圆最值---点心线
【例1】有一架靠在直角墙面的梯子(MN=4)正在下滑,D点出有一只猫紧紧盯住位于梯子MN的正中间E处的老鼠,等待与老鼠距离最小时扑捉.把墙面,梯子,猫和老鼠看成同一平面内的线或点,点D到BA,BC的距离分别为4和2.猫与老鼠的距离DE的最小值为_______.
N
A
D
E
M
C
B
2 5-2
考点4-1
针对训练
点圆最值---点心线
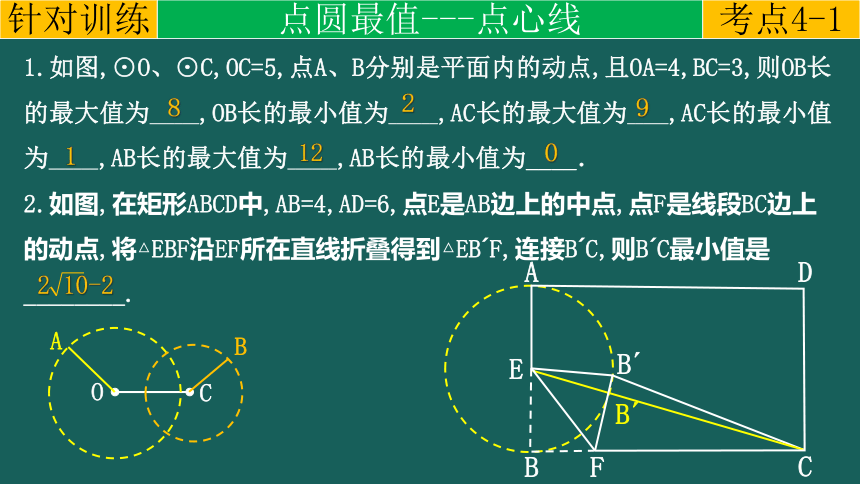
1.如图,⊙O、⊙C,OC=5,点A、B分别是平面内的动点,且OA=4,BC=3,则OB长的最大值为______,OB长的最小值为______,AC长的最大值为_____,AC长的最小值为______,AB长的最大值为______,AB长的最小值为____.
2.如图,在矩形ABCD中,AB=4,AD=6,点E是AB边上的中点,点F是线段BC边上的动点,将△EBF沿EF所在直线折叠得到△EB F,连接B C,则B C最小值是________.
1
8
2
9
12
0
O
C
A
B
B
E
F
C
D
B
B
2 10-2
A
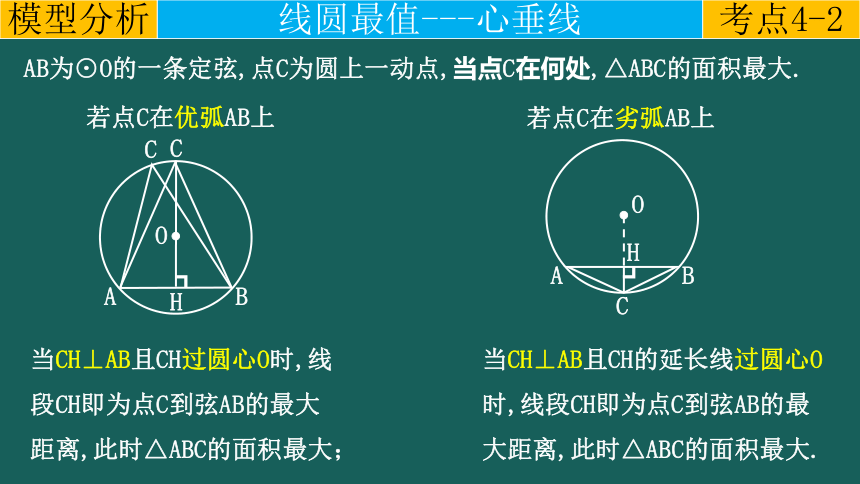
AB为⊙O的一条定弦,点C为圆上一动点,当点C在何处,△ABC的面积最大.
考点4-2
模型分析
线圆最值---心垂线
当CH⊥AB且CH的延长线过圆心O时,线段CH即为点C到弦AB的最大距离,此时△ABC的面积最大.
C
H
若点C在优弧AB上
O
B
A
C
当CH⊥AB且CH过圆心O时,线段CH即为点C到弦AB的最大距离,此时△ABC的面积最大;
O
C
B
A
H
若点C在劣弧AB上
考点4-2
典例精讲
线圆最值---心垂线
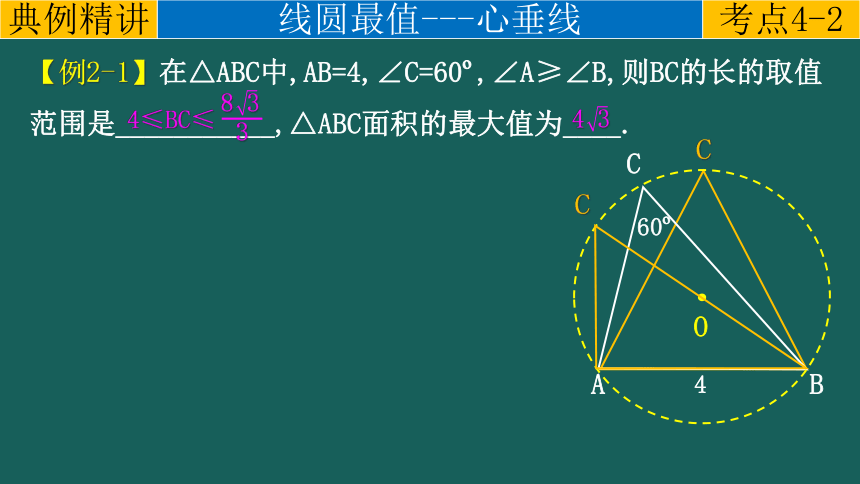
【例2-1】在△ABC中,AB=4,∠C=60 ,∠A≥∠B,则BC的长的取值范围是___________,△ABC面积的最大值为____.
C
C
A
B
60
4
O
C
4≤BC≤
8 3
3
4 3
考点4-2
模型分析
线圆最值---心垂线
O
l
如图,⊙O与直线l相离,点P是⊙O上的一个动点,设圆心O到直线l的距离为d,⊙O的半径为r,则点P到直线l的最小距离是____,点P到直线l的最大距离是_____.
d-r
d+r
A
B
P
H
M
∵OP+PM>OM>OH=OB+BH,OB=OP.
∵AH=OA+OH=OP+OH>PH>PM,
①线圆之间,心垂线截距最短(长).
结论:AH最长,BH最短.
∴PM>BH.
∴AH>PM.
考点4-2
典例精讲
线圆最值---心垂线
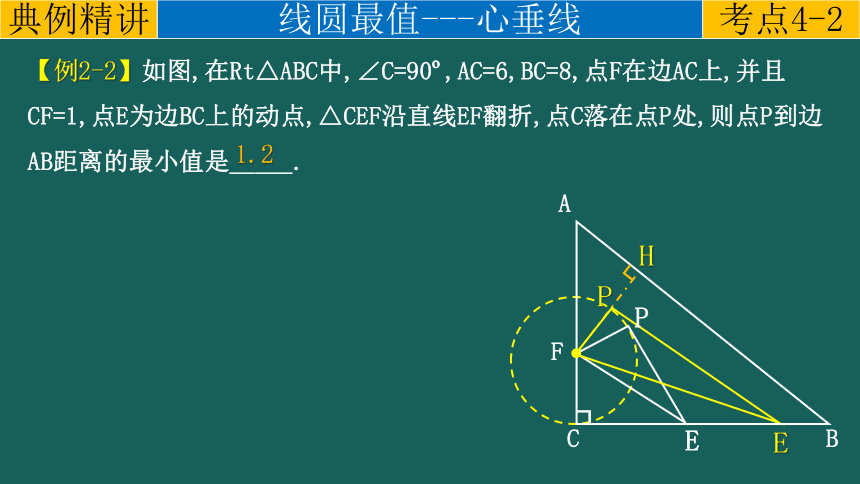
【例2-2】如图,在Rt△ABC中,∠C=90 ,AC=6,BC=8,点F在边AC上,并且CF=1,点E为边BC上的动点,△CEF沿直线EF翻折,点C落在点P处,则点P到边AB距离的最小值是_____.
P
P
H
E
A
F
C
B
E
1.2
考点4-3
模型分析
圆中最长弦---直径
1.定圆中最长的弦是直径;
O
B
A
D
C
2.定弦中最小的圆是以该弦为直径的圆
A
B
O
B
A
3.经过圆中定点最短的弦是垂直于过这点直径的弦;
O
P
C
D
E
F
H
考点4-3
典例精讲
圆中最长弦---直径
【例3-1】在△ABC中,∠ACB=90 ,AC=6,BC=8,O为AB的中点,过O作OE⊥OF,OE,OF分别交射线AC,BC于E,F,则EF的最小值为____.
【简答】∵∠EOF=∠C=90 ,
B
O
A
C
E
F
F
E
5
∴C,O均在以EF为直径的圆上.
∵EF是圆的直径,O、C均在圆上,且OC长度固定,要使EF最短,则圆最小,要使圆最小,由于OC为固定长度,则OC为直径时,圆最小,此时EF=CO=OA=OB=5(斜边上中线等于斜边一半)
考点4-3
典例精讲
圆中最长弦---直径
【例3-2】如图,P为⊙O内的一个定点,A为⊙O上的一个动点,射线AP,AO分别与⊙O交于点B,C.若⊙O的半径为3,OP=,则弦BC长的最大值为( )
A.2 B.3 C. D.3
A
C
A
B
P
O
A
C
B
考点4-4
模型分析
定角夹定高
【题型背景】在一些最值问题中,给定一个角,并且过定角的顶点作对边的垂线为定值时,也存在最值问题,面对这种问题我们借助“隐圆”进行说明:我们称这种问题为:“定角夹定高”模型也称“探照灯”模型.主要解决:
(1)线段最短问题; (2)面积最小问题.
【模型】如右图所示,在△ABC中,∠BAC=α为定值,AD为BC边上的高,且AD=h为定值,则底边BC存在最小值,△ABC的面积存在最小值.
A
h
D
C
B
α
O
α
E
【突破点】1.找出“隐圆”---三角形外接圆;
2.定高过外心(半径+弦心距)≥定高.
证明:作△ABC的外接圆,圆心为O,连接AO,BO,CO,
作OE⊥BC于点E.易得∠BOE=α,则OE=r·cosα.
∵OA+OE≥AD,
∴r+r·cosα≥h.
∴r≥
h
1+cosα
∴BE=r·sinα≥
h·sinα
1+cosα
∴BC=2BE≥
2h·sinα
1+cosα
∴S△ABCmin=
h2·sinα
1+cosα
考点4-4
典例精讲
定角夹定高
【例3-1】如图,在△ABC中,∠BAC=60 ,BC边上的高AD为3,则BC的最小值为___.
O
60
E
A
D
C
B
60
解:作△ABC的外接圆,连接OA,OB,OC,
设半径为r,
则∠BOC=2∠A=2×60=120
∵OB=OC.
∴∠BOE=60 .
∴OE=0.5r.
由垂线段最短可知:
OA+OE≥AD
作OE⊥BC于点E.
6
O
A
C
B
D
BC=2BE=
3r.
即:r+ r≥
1
2
3 3
解得:r≥
2 3
∴BC最小= =6.
3r
考点4-4
典例精讲
定角夹定高
【例3-2】(2022 T23)【拓展应用】将任意一个锐角的顶点放在正方形中心O处,该锐角记为∠GOH(设∠GOH=α),将∠GOH绕点O逆时针旋转,在旋转过程中,∠GOH的两边与正方形ABCD的边所围成的图形的面积为S2,请直接写出S2的最小值与最大值(分别用含α的式子表示).
A
O
C
D
B
G
N
M
H
Q
(F)
提升能力
强化训练
与“圆”有关的最值问题
1.如图,在矩形ABCD中,AB=3,BC=4,O为矩形ABCD的中心,以D为圆心,1为半径作⊙D,P为⊙D上的一个动点,连接AP,OP,AO,则△AOP面积的最大值为_______.
2.如图,在边长为2的菱形ABCD中,∠A=60 ,M是AD边的中点,N是AB上一个动点,将△AMN沿MN所在直线翻折得到△A MN,连接A C,则A C长的最小值为______.
17
4
A
P
O
D
C
B
7-1
A
A
N
M
D
C
B
提升能力
强化训练
与“圆”有关的最值问题
3.如图,在矩形ABCD中,AB=60,AD=45,P,Q分别是AB,AD边上的动点,PQ=52,以PQ为直径的⊙O与BD交于点M,N,则MN的最大值为_____.
A
B
C
D
Q
P
M
N
O
H
O
N
M
Q
P
∵MN=2NH=
∴当OH最短时,MN最长.
48
ON2-OH2
= 262-OH2
提升能力
强化训练
与“圆”有关的最值问题
4.如图,在Rt△ABC中,∠C=90 ,BC=6,AC=8,D,E分别是BC,AC上的一点,且DE=6.若以DE为直径的圆与斜边AB相交于M,N两点,则MN的最大值为_____. 5.如图,在⊙O中,直径AB=12,点D是圆上任意一点(A,B除外),P为CD的中点,过点D作DE⊥AB于点E,连接AD,EP.则EP的最大值为____.
24/5
A
O
M
D
E
C
B
N
A
C
D
O
E
B
P
F
6
提升能力
强化训练
与“圆”有关的最值问题
6.如图,AB是⊙O的弦,点C是ACB上的动点(C不与A,B重合),CH⊥AB,垂足为H,点M是BC的中点.若⊙O的半径是3,则MH长的最大值是_____.
7.如图,Rt△AOB∽Rt△DOC,∠AOB=∠COD=90 ,M为OA的中点,OA=5,OB=12.将△COD绕点O旋转,连接AD,CB,并延长交于点P,连接MP,则MP的最大值为_____.
3
︵
12.5
O
B
A
H
M
C
C
(M)
(H)
O
M
D
P
B
A
C
I
N
提升能力
强化训练
与“圆”有关的最值问题
10.如图,等边△ABC中,AB=6,P为AB上一动点,PD⊥BC,PE⊥AC,
(1)求∠DPE的度数;(2)求DE的最小值.
【简答】∵∠PEC=∠PDC=90 ,故四边形PDCE对角互补,故PDCE四点共圆,如图.
∠EOD=2∠ECD=120 ,要使得DE最小,则要使圆的半径最小,故直径PC最小,当CP⊥AB时,PC最短为 ,则可求出DE=4.5.
D
E
P
A
C
B
O
3 3
提升能力
强化训练
与“圆”有关的最值问题
11.如图,AC是半径为1的⊙的一条弦,点D是⊙O直径AB延长线上一点,AC=CD,BC=BD.(1)求证:直线CD是⊙O的切线;
(2)点P在弧AEB上运动,过点C作CP的垂线,与PA的延长线交于点F.
①当点P运动到与点C关于直径AB对称时,求PF的长;
②当点P运动到何处,PF取最大值 请直接写出此时点P的位置以及PF的长.
A
O
B
D
C
PF=2PC=2×2=4
PF=2PC=2 3
提升能力
强化训练
与“圆”有关的最值问题
4.点E在边长为4的正方形ABCD的边BC上,点F在边CD上,∠EAF=45 ,则△AEF面积的最小值为_________.
A
F
C
D
E
B
F
O
H
定角夹定高
16 2-16
提升能力
强化训练
与“圆”有关的最值问题
5.如图,半径为2cm,圆心角为90 的扇形OAB的弧AB上有一动点P,从点P向半径OA引垂线PH交OA于点H,设△OPH的内心为I,当点P在弧AB上从点A运动到点B时,内心I所经过的路径长为_____.
C
P
H
I
A
B
O
分析:连接AI,由内心的性质可得∠PIO=135 ,
定角夹定高
2π
2
90π 2
180
=
2
2
π
∵OI平分∠AOP,OP=OA,
∴△AIO≌△PIO,
∴∠AIO=∠PIO=135 ,
∵OA为定边,∠AIO=135 为定角.
∴P在以OA为弦且圆心角为90 的⊙C上运动.
由弧长公式可求得内心I的运动路径长为:
易求AC= 2.
提升能力
强化训练
与“圆”有关的最值问题
6.如图,已知以AB为直径的⊙O,C为弧AB的中点,P为弧BC上任意一点,CD⊥CP交AP于D,连接BD,若AB=6,则BD的最小值为_______.
G
A
P
C
O
B
D
分析:连接AC,易得∠P=45 ,
∴△CDP为等腰三角形,
∴∠ADC=135 为定角,AC为定边.
∴∠AGC=90 ,
∵AB=6,∴ ,∴AG=CG=3.
定角夹定高
3 5-3
提升能力
强化训练
与“圆”有关的最值问题
9.如图,在四边形ABCD中,AB=AD=CD=4,AD∥BC,∠B=60 ,点E、F分别为边BC、CD上两个动点,且∠EAF=60 ,则△AEF的面积是否存在最小值 若存在,求出其最小值;若不存在,请说明理由.
【简答】将△ADF绕点A顺时针旋转120 ,得△ABF ,则∠EAF =60 ,易证△AEF ≌△AEF,作△AEF 的外接圆⊙O,作OH⊥BC于点H,AG⊥BC于点G,则∠F OH=60 ,设⊙O的半径为r,则OH=0.5OF=0.5r.∵OA+OH≥AG,
A
E
C
F
D
B
O
G
H
F
定角夹定高
提升能力
强化训练
与“圆”有关的最值问题
A
C
D
F
E
B
C
B
F
E
45
F
O
45
H
10.在四边形ABCD中,∠BAD=45 ,∠B=∠D=90 ,CB=CD=,点E、F分别为AB、AD上的点,若保持CE⊥CF,那么四边形AECF的面积是否存在最大值,若存在,求出面积的最大值;若不存在,请说明理由.
定角夹定高
同课章节目录
