专题4.5圆---利用“瓜豆”模型求最值-中考数学二轮复习必会几何模型剖析(全国通用)
文档属性
| 名称 | 专题4.5圆---利用“瓜豆”模型求最值-中考数学二轮复习必会几何模型剖析(全国通用) |  | |
| 格式 | pptx | ||
| 文件大小 | 6.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-25 10:14:25 | ||
图片预览






文档简介
(共26张PPT)
专题四 与圆有关的模型
人教版中考第二轮总复习---几何模型
§4.5 利用“瓜豆”模型求最值
“主从联动模型”在网络上也叫“瓜豆模型”,出自成语“种瓜得瓜,种豆得豆”.在这一类动点问题中,一个动点随另一个动点的运动而运动,我们把它们分别叫做从动点和主动点,从动点和主动点的轨迹是一致的,即所谓“种瓜得瓜,种豆得豆”.解决这一类问题通常用到旋转和放缩,也就是我们常说的全等型和相似型的手拉手模型.
知识要点
模型分析
主从联动模型专题
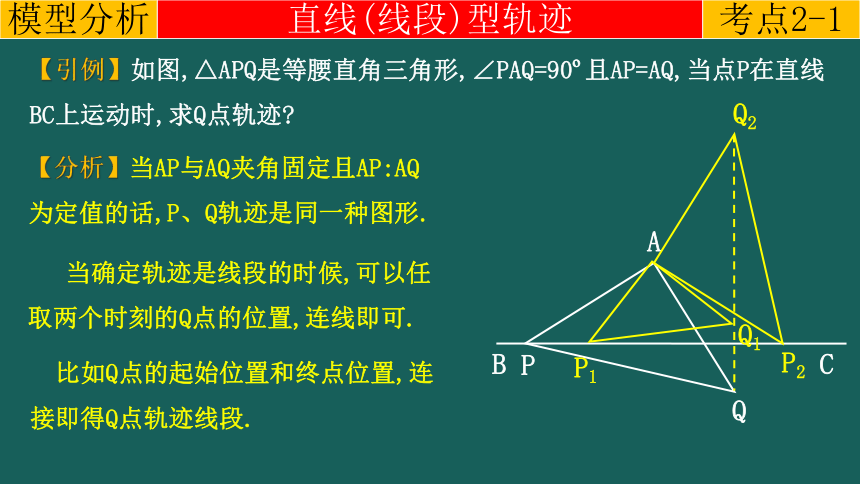
【引例】如图,△APQ是等腰直角三角形,∠PAQ=90 且AP=AQ,当点P在直线BC上运动时,求Q点轨迹
【分析】当AP与AQ夹角固定且AP:AQ为定值的话,P、Q轨迹是同一种图形.
C
B
P
Q
A
Q2
P2
P1
Q1
考点2-1
模型分析
直线(线段)型轨迹
当确定轨迹是线段的时候,可以任取两个时刻的Q点的位置,连线即可.
比如Q点的起始位置和终点位置,连接即得Q点轨迹线段.
考点2-1
典例精讲
直线(线段)型轨迹
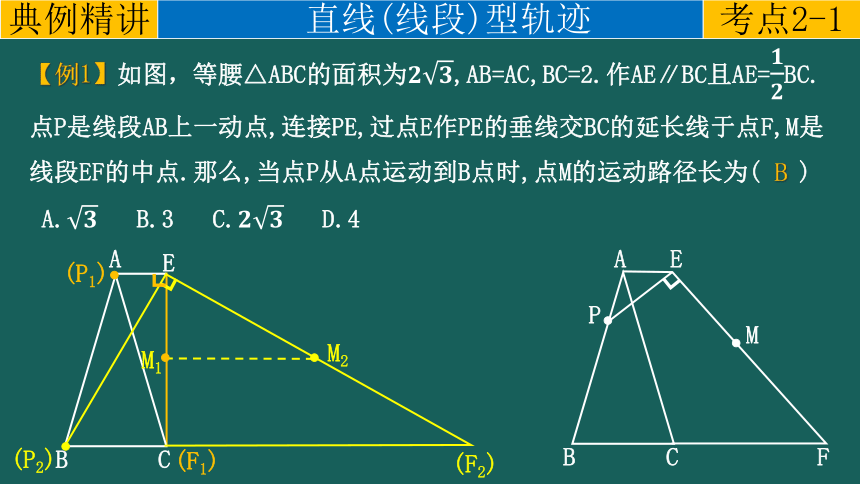
【例1】如图,等腰△ABC的面积为,AB=AC,BC=2.作AE∥BC且AE=BC.点P是线段AB上一动点,连接PE,过点E作PE的垂线交BC的延长线于点F,M是线段EF的中点.那么,当点P从A点运动到B点时,点M的运动路径长为( )
A. B.3 C. D.4
B
A
M
E
P
F
C
B
A
E
C
B
(P1)
(F2)
M1
M2
(F1)
(P2)
考点2-1
典例精讲
直线(线段)型轨迹
【例1】如图,正方形ABCD的边长为2,动点E从点A出发,沿边AB向终点B运动,以DE为边作正方形DEFG(点D、E、F、G按顺时针方向排列).在点E的整个运动过程中,点F经过的路径长为______.
A
C
G
F
B
E
D
【分析】点E是主动点,点F是从动点,连接DF,我们可以这么看,DE绕点D顺时针旋转45 并放大为DE的 倍,即得DF,而点E的运动轨迹为线段AB,那么点F的路径长必为线段AB绕点D顺时针旋转45 ,并放大为原来的倍的路径长.
2
2
解析:易证△ADE∽△BDF,因此∠FBD=90 .
∴F经过的路径长为AB,即2 2.
2
∵E点运动路径长为AB.
∴F点运动轨迹为线段,BF=AE.
2
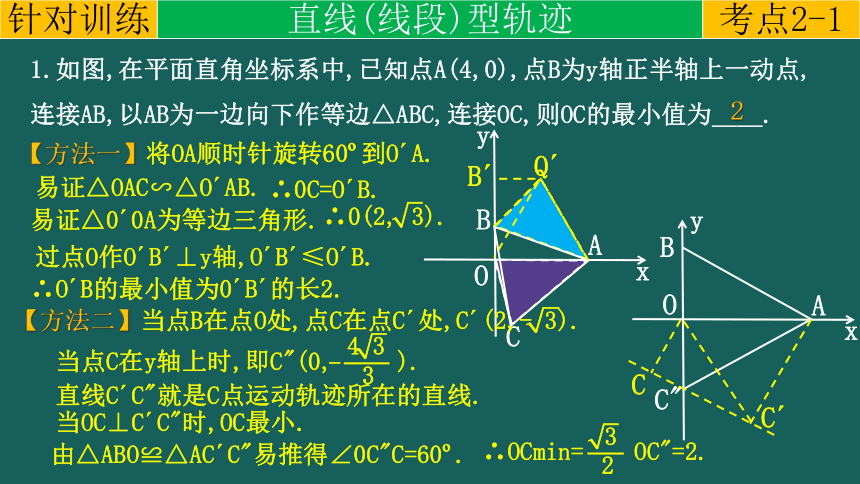
1.如图,在平面直角坐标系中,已知点A(4,0),点B为y轴正半轴上一动点,连接AB,以AB为一边向下作等边△ABC,连接OC,则OC的最小值为____.
【方法一】将OA顺时针旋转60 到O A.
∴O B的最小值为0 B 的长2.
易证△OAC∽△O AB.
∴0C=O B.
易证△0 0A为等边三角形.
过点O作O B ⊥y轴,O B ≤O B.
2
∴0(2, 3).
y
O
x
C
A
B
B
Q
由△ABO≌△AC C"易推得∠0C"C=60 .
当点C在y轴上时,即C"(0, ).
当OC⊥C C"时,OC最小.
4 3
3
-
直线C C"就是C点运动轨迹所在的直线.
【方法二】当点B在点O处,点C在点C 处,C (2,- 3).
∴OCmin= OC"=2.
3
2
y
O
x
C"
A
B
C
C
考点2-1
针对训练
直线(线段)型轨迹
2.如图,△ABC中,∠ACB=90 ,∠A=30 ,BC=2,D是AB上一动点,以DC为斜边向上作等腰Rt△DCE,使∠CED=90 ,连接BE,求BE的最小值.
A
D
E
C
B
F
H
G
【分析】E是由D绕C点逆时针旋转45 并缩小为√2/2倍得到的,因此如果把△ABC绕着C点逆时针旋转45 ,并缩小为√2/2倍得到△GFC,则FG就是E点的运动轨迹.
【简答】分别以BC,AC为斜边构造等腰直角△BFC,△AGC.
易证明△ACD∽△GCE,△FCG∽△BCA,
∴△CFE∽△CBD,
∴∠CFE=∠CBD,
∴∠CFE=∠CFG=60 ,
∴F,E,G三点共线,
∴∠BFH=30 ,
∴BH= BP= ,即BE的最小值为 .
1
2
2
2
2
2
考点2-1
针对训练
直线(线段)型轨迹
【引例】如图,已知A是⊙O外一点,P是⊙O上的动点,线段AP的中点为Q,连接OA,OP.若⊙O的半径为2,OA=4,则线段OQ的最小值是( )
A.0 B.1 C.2 D.3
B
考点2-2
典例精讲
圆型运动轨迹
A
Q
P
O
M
【思考】当点P在圆O上运动时,Q点轨迹是?
解:连接AO,取AO的中点M,连接QM,PO.
∴QM是△APO的中位线.
∴QM=0.5PO=0.5r.
∴点Q在以M为圆心,0.5r为半径的圆上.
古人云:种瓜得瓜,种豆得豆.种圆得圆,种线得线,谓之“瓜豆原理”.
【关键】根据图中的主动点和从动点,找出主从动点的运动路径.
【变式1】如图,P是半径为r的⊙O上一个动点,A为定点,
连接AP,作AQ⊥AP且AQ=AP.
解:连接AO,过点A作AM⊥AO,使AM=AO,连接OP,MQ,
O
A
P
Q
易证△APO≌△AQM(SAS).
∴QM=PO=r
∴Q在以点M为圆心,r为半径的圆上.
AP=2AQ
O
A
P
Q
解:连接AO,过点A作AM⊥AO,使AM=AO,连接OP,MQ,
易证△APO∽△AQM.
∴QM:PO=AQ:AP=1:2
∴Q在以点M为圆心,0.5r为半径的圆上.
∴QM=0.5PO=0.5r
M
M
【思考】当点P在圆O上运动时,Q点轨迹是?
考点2-2
模型分析
圆型运动轨迹
【变式2】如图,P是圆O上一个动点,A为定点,连接AP,
以AP为边作等边△APQ.
解:连接AO,将AO绕点A逆时针旋转60 得AM,连接OP,MQ,
O
A
P
Q
易证△APO≌△AQM(SAS).
∴Q在以点M为圆心,r为半径的圆上.
∴QM=PO=r.
O
A
P
Q
解:连接AO,将AO绕点A逆时针旋转45 得AM,连接OP,MQ,
易证△APO∽△AQM.
M
以AP为斜边作等腰直角△APQ.
M
【考虑】当点P在圆O上运动时,Q点轨迹是
∴QM:PO=AQ:AP=1:
2
∴QM= PO= r
2
2
2
2
∴Q在以点M为圆心, r为半径的圆上.
5
2
考点2-2
模型分析
圆型运动轨迹
【总结】为了便于区分动点P,Q,可称点P为主动点,点Q为从动点.此类问题的必要条件(两个定量):主、从动点与定点连线的夹角是定量(∠PAQ是定值);主、从动点到定点的距离之比是定量(AP:AQ是定值).
(1)主、从动点与定点连线的夹角等于两圆心与定点连线的夹角:∠OAM=∠PAQ;
O
A
P
Q
M
(2)主、从动点与定点的距离之比等于两圆心到定点的距离之比:AP:AQ=AO:AM,也等于两圆半径之比.按以上两点即可确定从动点轨迹圆,Q与P的关系相当于旋转+伸缩.
古人云:种瓜得瓜,种豆得豆.种圆得圆,种线得线,谓之“瓜豆模型”.
考点2-2
模型分析
圆型运动轨迹
考点2-2
典例精讲
圆型运动轨迹
【例1】平面内两定点A、B之间的距离为8,P为一动点,且PB=2,连接AP,并且以AP为斜边在AP的上方作等腰直角△APC,如图,连接BC,则BC的最大值与最小值的差为________.
A
B
P
C
B
【简答】点P在以B为圆心,2为半径的圆上运动,属于主动点,点C可以看做是由点P绕点A逆时针旋转90 ,再缩小 倍而得到的,所以点P所在圆的圆心绕点A逆时针旋转90 ,再乘以 就是点C所在圆的圆心B ,而半径也缩小 倍,即 .根据点圆最值模型,可知:BB -CB ≤BC≤BB +CB ,即 ≤BC≤ ,因此最大值与最小值的差为 .
2
2
2
2
2
2
2
3 2
5 2
3 2
1.如图,四边形ABCD中,BC=4,∠BAC=∠ADC=90 ,AD=CD,则BD的最大值为__
【简答】取BC的中点E,连接AE,则AE=2,以EC为斜边,向上构造等腰直角△ECF如图,连接FD、FB,易证△AEC△DFC,相似比为√,DF=压,过F作FHLBC,易求得BF=√i⑥,因此BD≤BF+FD=√10+√2.
A
D
C
B
E
F
H
考点2-2
针对训练
圆型运动轨迹
【分析】B,C是定点,∠BAC=90 ,因此点A的轨迹是以AB为直径的圆,设其圆心为E,△ADC始终个等腰直角三角形,因此点D是由点A绕着点C顺时针旋转45 ,并缩小为是 倍得到的,∴点D的轨迹也是圆,其圆心是由点E绕着点C顺时针旋转45 并缩小为 倍而得到,也就是以CE为斜边构造等腰直角△ECF,所以点D的轨迹就是以F为圆心,以FC为半径的圆,∴BD≤BF+FD,当B,F,D三点共线时,取得最值.过F作FH⊥BC,易求得BF= ,FD=FC= ,∴BD的最大值为
2
2
2
2
10
2
10
2.如图,正方形ABCD中,AB=4,B,F分别是AB、AD上的动点,AE=DF,连接DE,CF交于点P,过P作PK∥BC,且PK=2,当∠CBK的度数最大,BK=______.
【简答】易证∠DPC=90 ,∴点P在以CD为直径的⊙O上运动,由于K是由P向右平移2个单位得到的,∴K在⊙Q上运动,当BK⊥QK时,∠CBK最大,此时BK=B C=-6.如果题目是解答题,书写过程不能出现“瓜豆原理,主从联动”等字样,要利用相似去进行规范书写证明.
A
E
F
C
D
B
P
K
O
Q
C
考点2-2
针对训练
圆型运动轨迹
3.如图,在矩形ABCD中,AB=4,AD=3,点E在边AB上,且AE=3BE,将线段AE绕点A旋转一定的角度α(0 <α<360 ),得到线段AF,点M是线段CF的中点,则旋转过程中线段BM长的最大值为___,和最小值为___.
考点2-2
针对训练
圆型运动轨迹
D
E
F
C
B
A
O
M
M
M
4
1
4.如图,在△ABC中,∠ACB=90 ,AC=BC=4,将AC绕点A逆时针旋转α(0 <α<360 ),得到AC ,连接BC ,E为BC 的中点,连接CE,则CE长度的取值范围___________________.
考点2-2
针对训练
圆型运动轨迹
A
C
B
C
O
E
E
E
≤CE≤
2 2-2
2 2+2
知识梳理
课堂小结
“瓜豆”模型
两定三动求轨迹
条件
结论
两个动点与定点连线的夹角确定不变为α主动点、从动点与定点的两连线的比为定值K一个定点保持不动(无定不瓜豆)—旋转中心
从路径相似于主路径(且位似)其相似比为K
从路径=K·主路径(秒杀公式)
从路径:看作主路径绕定点旋转定角并按照定比缩放形成
(定点、定角、定比)
知识梳理
课堂小结
“瓜豆”模型—“V”型动点轨迹
【条件】三定两动---三定:定点;定角;定比。
如图:O为定点;∠POQ为定角;QO:PQ=K(为定值)
两动:P、Q为两个动点,P为主动点,Q为从动点.(捆绑运动)
【问题】通过P点的轨迹求得Q点的轨迹.
【结论】点P的运动轨迹与Q的运动轨迹形状相同(相似,且位似).Q的轨迹的长度:P的运动轨迹=K(定比)即:Q的轨迹的长度=K·P的运动轨迹
【瓜豆原理】种瓜得瓜;种豆得豆.满足“三定两动”条件的两个动点的轨迹:相似、位似.且从动点的轨迹=主动点的轨迹·定比(K).定比K为两轨迹的相似比!
上述模型在数学江湖中也被称作“捆绑动点轨迹模型”
O
P
Q
1.如图,正方形ABCD中,AB=12,E是BC边上一点,CE=7,F是正方形内部一点,且EF=3,连接EF,DE,DF,并将△DEF绕点D逆时针旋转90 得到△DMN(点M,N分别为点E,F的对应点),连接CN,则CN长度的最小值为_____.
提升能力
强化训练
“瓜豆”模型
F
A
M
E
D
C
B
N
N
H
10
1.如图,△ABC为等腰直角三角形,点A(0,3),B(-3,0),点D是x轴上一个动点,从点B开始向右运动,以AD为一直角边在其右侧作等腰直角△ADE,
∠DAE=90 ,若△ABD为等腰三角形,则点E的坐标为___________________.
y
x
O
B
A
C
D
E
先证△ABD≌△ACE
∠ACE=∠ABD=45
CE⊥BC
D1
E1
D2
E2
D3
E3
提升能力
强化训练
“瓜豆”模型
(3,3)(3,6)或(3,3 2)
【分析】1.先画出Rt△ABP的起始位置,和终止位置;
2.在再证明△AP1P2∽△AB1B2;
3.点B的运动轨迹是线段B1B2.
2.如图,已知点A是第一象限内横坐标为的定点,AN⊥x轴于点M,交直线y=-x于点N.若点P是线段ON上的一个动点,∠APB=30 ,BA⊥PA,则点P在线段ON上的一个运动时,A点不变,B点随之运动,求当点P从点O运动到点N时,点B运动的路径长是( ) A.2 B. C. D.
C
P
B
A
y
x
O
M
N
P2
B2
P1
B1
提升能力
强化训练
“瓜豆”模型
=
B1B2=
ON
3
=
3·2
3
=
2
M
N
3.如图所示,AB=4,AC=2,以BC为底边向上构造等腰直角△BCD,连接AD并延长至点P,使AD=PD,则PB的取值范围为_______.
【分析】固定AB不变,AC=2,则点C的轨迹是以A为圆心,2为半径的圆,以BC为斜边作等腰直角△BCD,则点D的轨迹是以点M为圆心、 为半径的圆.
∵AP=2AD,故点P轨迹是以N为圆心, 为半径的圆,即可求出PB的取值范围.
A
C
D
P
B
提升能力
强化训练
“瓜豆”模型
2
2 2
4.如图,点P(3,4),圆P半径为2,A(2.8,0),B(5.6,0),点M是圆P上的动点,点C是MB的中点,则AC的最小值是_____.
1.5
B
y
x
O
A
P
C
M
N
M
C
y
x
O
B
A
P
C
M
M
C
提升能力
强化训练
“瓜豆”模型
种圆得圆
5.如图,在等腰Rt△ABC中,∠BAC=90 ,AB=3,点D在BC上,以AD为边向右作正方形ADEF,连接BF,若∠FBC=30 ,则BD=____.
6.如图,等边△ABC的边长为8,点D为AB边上一动点,DE始终平行于BC,MN为△ADE的中位线,现将点D开始沿AB方向移动,移动到点B处停止,在整个移动过程中线段MN扫过的面积是_____.
△ABD≌△ACF,BD=FC
A
F
E
C
D
B
6
提升能力
强化训练
“瓜豆”模型
A
M
D
E
C
B
N
4 3
7.如图,△ABC是边长为4的等边三角形,AD为BC边上的高,点E为线段AD上一动点,连接EF,CE,将CE绕点C逆时针旋转60 得到线段CF,连接DF.△CEF的周长的最小值为____,DF的最小值是_____.
G
A
D
E
F
C
B
1
6
【方法一】连接BF,可得△CFB≌△CAE,
∴∠CBF=∠CAE=30 ,∴点F在射线BF上,
当DF⊥BF时,DF最短,
【方法二】取AC的中点G,连接EG,
可得△CFD≌△CEG,∴DF=EG,由垂线段最短得:
当GE⊥AD时GE最短,即DF最短。
提升能力
强化训练
“瓜豆”模型
8.如图,在等边△ABC中,AB=10,BD=4,BE=2,点P从点E出发沿EA方向运动,连结PD,以PD为边,在PD的右侧按如图所示的方式作等边△DPF,当点P从点E运动到点A时,点F运动的路径长是____.
【分析】根据△DPF是等边三角形,所以可知F点运动路径长与P点相同,P从E点运动到A点路径长为8,故此题答案为8.
A
D
F
P
E
C
B
8
提升能力
强化训练
“瓜豆”模型
专题四 与圆有关的模型
人教版中考第二轮总复习---几何模型
§4.5 利用“瓜豆”模型求最值
“主从联动模型”在网络上也叫“瓜豆模型”,出自成语“种瓜得瓜,种豆得豆”.在这一类动点问题中,一个动点随另一个动点的运动而运动,我们把它们分别叫做从动点和主动点,从动点和主动点的轨迹是一致的,即所谓“种瓜得瓜,种豆得豆”.解决这一类问题通常用到旋转和放缩,也就是我们常说的全等型和相似型的手拉手模型.
知识要点
模型分析
主从联动模型专题
【引例】如图,△APQ是等腰直角三角形,∠PAQ=90 且AP=AQ,当点P在直线BC上运动时,求Q点轨迹
【分析】当AP与AQ夹角固定且AP:AQ为定值的话,P、Q轨迹是同一种图形.
C
B
P
Q
A
Q2
P2
P1
Q1
考点2-1
模型分析
直线(线段)型轨迹
当确定轨迹是线段的时候,可以任取两个时刻的Q点的位置,连线即可.
比如Q点的起始位置和终点位置,连接即得Q点轨迹线段.
考点2-1
典例精讲
直线(线段)型轨迹
【例1】如图,等腰△ABC的面积为,AB=AC,BC=2.作AE∥BC且AE=BC.点P是线段AB上一动点,连接PE,过点E作PE的垂线交BC的延长线于点F,M是线段EF的中点.那么,当点P从A点运动到B点时,点M的运动路径长为( )
A. B.3 C. D.4
B
A
M
E
P
F
C
B
A
E
C
B
(P1)
(F2)
M1
M2
(F1)
(P2)
考点2-1
典例精讲
直线(线段)型轨迹
【例1】如图,正方形ABCD的边长为2,动点E从点A出发,沿边AB向终点B运动,以DE为边作正方形DEFG(点D、E、F、G按顺时针方向排列).在点E的整个运动过程中,点F经过的路径长为______.
A
C
G
F
B
E
D
【分析】点E是主动点,点F是从动点,连接DF,我们可以这么看,DE绕点D顺时针旋转45 并放大为DE的 倍,即得DF,而点E的运动轨迹为线段AB,那么点F的路径长必为线段AB绕点D顺时针旋转45 ,并放大为原来的倍的路径长.
2
2
解析:易证△ADE∽△BDF,因此∠FBD=90 .
∴F经过的路径长为AB,即2 2.
2
∵E点运动路径长为AB.
∴F点运动轨迹为线段,BF=AE.
2
1.如图,在平面直角坐标系中,已知点A(4,0),点B为y轴正半轴上一动点,连接AB,以AB为一边向下作等边△ABC,连接OC,则OC的最小值为____.
【方法一】将OA顺时针旋转60 到O A.
∴O B的最小值为0 B 的长2.
易证△OAC∽△O AB.
∴0C=O B.
易证△0 0A为等边三角形.
过点O作O B ⊥y轴,O B ≤O B.
2
∴0(2, 3).
y
O
x
C
A
B
B
Q
由△ABO≌△AC C"易推得∠0C"C=60 .
当点C在y轴上时,即C"(0, ).
当OC⊥C C"时,OC最小.
4 3
3
-
直线C C"就是C点运动轨迹所在的直线.
【方法二】当点B在点O处,点C在点C 处,C (2,- 3).
∴OCmin= OC"=2.
3
2
y
O
x
C"
A
B
C
C
考点2-1
针对训练
直线(线段)型轨迹
2.如图,△ABC中,∠ACB=90 ,∠A=30 ,BC=2,D是AB上一动点,以DC为斜边向上作等腰Rt△DCE,使∠CED=90 ,连接BE,求BE的最小值.
A
D
E
C
B
F
H
G
【分析】E是由D绕C点逆时针旋转45 并缩小为√2/2倍得到的,因此如果把△ABC绕着C点逆时针旋转45 ,并缩小为√2/2倍得到△GFC,则FG就是E点的运动轨迹.
【简答】分别以BC,AC为斜边构造等腰直角△BFC,△AGC.
易证明△ACD∽△GCE,△FCG∽△BCA,
∴△CFE∽△CBD,
∴∠CFE=∠CBD,
∴∠CFE=∠CFG=60 ,
∴F,E,G三点共线,
∴∠BFH=30 ,
∴BH= BP= ,即BE的最小值为 .
1
2
2
2
2
2
考点2-1
针对训练
直线(线段)型轨迹
【引例】如图,已知A是⊙O外一点,P是⊙O上的动点,线段AP的中点为Q,连接OA,OP.若⊙O的半径为2,OA=4,则线段OQ的最小值是( )
A.0 B.1 C.2 D.3
B
考点2-2
典例精讲
圆型运动轨迹
A
Q
P
O
M
【思考】当点P在圆O上运动时,Q点轨迹是?
解:连接AO,取AO的中点M,连接QM,PO.
∴QM是△APO的中位线.
∴QM=0.5PO=0.5r.
∴点Q在以M为圆心,0.5r为半径的圆上.
古人云:种瓜得瓜,种豆得豆.种圆得圆,种线得线,谓之“瓜豆原理”.
【关键】根据图中的主动点和从动点,找出主从动点的运动路径.
【变式1】如图,P是半径为r的⊙O上一个动点,A为定点,
连接AP,作AQ⊥AP且AQ=AP.
解:连接AO,过点A作AM⊥AO,使AM=AO,连接OP,MQ,
O
A
P
Q
易证△APO≌△AQM(SAS).
∴QM=PO=r
∴Q在以点M为圆心,r为半径的圆上.
AP=2AQ
O
A
P
Q
解:连接AO,过点A作AM⊥AO,使AM=AO,连接OP,MQ,
易证△APO∽△AQM.
∴QM:PO=AQ:AP=1:2
∴Q在以点M为圆心,0.5r为半径的圆上.
∴QM=0.5PO=0.5r
M
M
【思考】当点P在圆O上运动时,Q点轨迹是?
考点2-2
模型分析
圆型运动轨迹
【变式2】如图,P是圆O上一个动点,A为定点,连接AP,
以AP为边作等边△APQ.
解:连接AO,将AO绕点A逆时针旋转60 得AM,连接OP,MQ,
O
A
P
Q
易证△APO≌△AQM(SAS).
∴Q在以点M为圆心,r为半径的圆上.
∴QM=PO=r.
O
A
P
Q
解:连接AO,将AO绕点A逆时针旋转45 得AM,连接OP,MQ,
易证△APO∽△AQM.
M
以AP为斜边作等腰直角△APQ.
M
【考虑】当点P在圆O上运动时,Q点轨迹是
∴QM:PO=AQ:AP=1:
2
∴QM= PO= r
2
2
2
2
∴Q在以点M为圆心, r为半径的圆上.
5
2
考点2-2
模型分析
圆型运动轨迹
【总结】为了便于区分动点P,Q,可称点P为主动点,点Q为从动点.此类问题的必要条件(两个定量):主、从动点与定点连线的夹角是定量(∠PAQ是定值);主、从动点到定点的距离之比是定量(AP:AQ是定值).
(1)主、从动点与定点连线的夹角等于两圆心与定点连线的夹角:∠OAM=∠PAQ;
O
A
P
Q
M
(2)主、从动点与定点的距离之比等于两圆心到定点的距离之比:AP:AQ=AO:AM,也等于两圆半径之比.按以上两点即可确定从动点轨迹圆,Q与P的关系相当于旋转+伸缩.
古人云:种瓜得瓜,种豆得豆.种圆得圆,种线得线,谓之“瓜豆模型”.
考点2-2
模型分析
圆型运动轨迹
考点2-2
典例精讲
圆型运动轨迹
【例1】平面内两定点A、B之间的距离为8,P为一动点,且PB=2,连接AP,并且以AP为斜边在AP的上方作等腰直角△APC,如图,连接BC,则BC的最大值与最小值的差为________.
A
B
P
C
B
【简答】点P在以B为圆心,2为半径的圆上运动,属于主动点,点C可以看做是由点P绕点A逆时针旋转90 ,再缩小 倍而得到的,所以点P所在圆的圆心绕点A逆时针旋转90 ,再乘以 就是点C所在圆的圆心B ,而半径也缩小 倍,即 .根据点圆最值模型,可知:BB -CB ≤BC≤BB +CB ,即 ≤BC≤ ,因此最大值与最小值的差为 .
2
2
2
2
2
2
2
3 2
5 2
3 2
1.如图,四边形ABCD中,BC=4,∠BAC=∠ADC=90 ,AD=CD,则BD的最大值为__
【简答】取BC的中点E,连接AE,则AE=2,以EC为斜边,向上构造等腰直角△ECF如图,连接FD、FB,易证△AEC△DFC,相似比为√,DF=压,过F作FHLBC,易求得BF=√i⑥,因此BD≤BF+FD=√10+√2.
A
D
C
B
E
F
H
考点2-2
针对训练
圆型运动轨迹
【分析】B,C是定点,∠BAC=90 ,因此点A的轨迹是以AB为直径的圆,设其圆心为E,△ADC始终个等腰直角三角形,因此点D是由点A绕着点C顺时针旋转45 ,并缩小为是 倍得到的,∴点D的轨迹也是圆,其圆心是由点E绕着点C顺时针旋转45 并缩小为 倍而得到,也就是以CE为斜边构造等腰直角△ECF,所以点D的轨迹就是以F为圆心,以FC为半径的圆,∴BD≤BF+FD,当B,F,D三点共线时,取得最值.过F作FH⊥BC,易求得BF= ,FD=FC= ,∴BD的最大值为
2
2
2
2
10
2
10
2.如图,正方形ABCD中,AB=4,B,F分别是AB、AD上的动点,AE=DF,连接DE,CF交于点P,过P作PK∥BC,且PK=2,当∠CBK的度数最大,BK=______.
【简答】易证∠DPC=90 ,∴点P在以CD为直径的⊙O上运动,由于K是由P向右平移2个单位得到的,∴K在⊙Q上运动,当BK⊥QK时,∠CBK最大,此时BK=B C=-6.如果题目是解答题,书写过程不能出现“瓜豆原理,主从联动”等字样,要利用相似去进行规范书写证明.
A
E
F
C
D
B
P
K
O
Q
C
考点2-2
针对训练
圆型运动轨迹
3.如图,在矩形ABCD中,AB=4,AD=3,点E在边AB上,且AE=3BE,将线段AE绕点A旋转一定的角度α(0 <α<360 ),得到线段AF,点M是线段CF的中点,则旋转过程中线段BM长的最大值为___,和最小值为___.
考点2-2
针对训练
圆型运动轨迹
D
E
F
C
B
A
O
M
M
M
4
1
4.如图,在△ABC中,∠ACB=90 ,AC=BC=4,将AC绕点A逆时针旋转α(0 <α<360 ),得到AC ,连接BC ,E为BC 的中点,连接CE,则CE长度的取值范围___________________.
考点2-2
针对训练
圆型运动轨迹
A
C
B
C
O
E
E
E
≤CE≤
2 2-2
2 2+2
知识梳理
课堂小结
“瓜豆”模型
两定三动求轨迹
条件
结论
两个动点与定点连线的夹角确定不变为α主动点、从动点与定点的两连线的比为定值K一个定点保持不动(无定不瓜豆)—旋转中心
从路径相似于主路径(且位似)其相似比为K
从路径=K·主路径(秒杀公式)
从路径:看作主路径绕定点旋转定角并按照定比缩放形成
(定点、定角、定比)
知识梳理
课堂小结
“瓜豆”模型—“V”型动点轨迹
【条件】三定两动---三定:定点;定角;定比。
如图:O为定点;∠POQ为定角;QO:PQ=K(为定值)
两动:P、Q为两个动点,P为主动点,Q为从动点.(捆绑运动)
【问题】通过P点的轨迹求得Q点的轨迹.
【结论】点P的运动轨迹与Q的运动轨迹形状相同(相似,且位似).Q的轨迹的长度:P的运动轨迹=K(定比)即:Q的轨迹的长度=K·P的运动轨迹
【瓜豆原理】种瓜得瓜;种豆得豆.满足“三定两动”条件的两个动点的轨迹:相似、位似.且从动点的轨迹=主动点的轨迹·定比(K).定比K为两轨迹的相似比!
上述模型在数学江湖中也被称作“捆绑动点轨迹模型”
O
P
Q
1.如图,正方形ABCD中,AB=12,E是BC边上一点,CE=7,F是正方形内部一点,且EF=3,连接EF,DE,DF,并将△DEF绕点D逆时针旋转90 得到△DMN(点M,N分别为点E,F的对应点),连接CN,则CN长度的最小值为_____.
提升能力
强化训练
“瓜豆”模型
F
A
M
E
D
C
B
N
N
H
10
1.如图,△ABC为等腰直角三角形,点A(0,3),B(-3,0),点D是x轴上一个动点,从点B开始向右运动,以AD为一直角边在其右侧作等腰直角△ADE,
∠DAE=90 ,若△ABD为等腰三角形,则点E的坐标为___________________.
y
x
O
B
A
C
D
E
先证△ABD≌△ACE
∠ACE=∠ABD=45
CE⊥BC
D1
E1
D2
E2
D3
E3
提升能力
强化训练
“瓜豆”模型
(3,3)(3,6)或(3,3 2)
【分析】1.先画出Rt△ABP的起始位置,和终止位置;
2.在再证明△AP1P2∽△AB1B2;
3.点B的运动轨迹是线段B1B2.
2.如图,已知点A是第一象限内横坐标为的定点,AN⊥x轴于点M,交直线y=-x于点N.若点P是线段ON上的一个动点,∠APB=30 ,BA⊥PA,则点P在线段ON上的一个运动时,A点不变,B点随之运动,求当点P从点O运动到点N时,点B运动的路径长是( ) A.2 B. C. D.
C
P
B
A
y
x
O
M
N
P2
B2
P1
B1
提升能力
强化训练
“瓜豆”模型
=
B1B2=
ON
3
=
3·2
3
=
2
M
N
3.如图所示,AB=4,AC=2,以BC为底边向上构造等腰直角△BCD,连接AD并延长至点P,使AD=PD,则PB的取值范围为_______.
【分析】固定AB不变,AC=2,则点C的轨迹是以A为圆心,2为半径的圆,以BC为斜边作等腰直角△BCD,则点D的轨迹是以点M为圆心、 为半径的圆.
∵AP=2AD,故点P轨迹是以N为圆心, 为半径的圆,即可求出PB的取值范围.
A
C
D
P
B
提升能力
强化训练
“瓜豆”模型
2
2 2
4.如图,点P(3,4),圆P半径为2,A(2.8,0),B(5.6,0),点M是圆P上的动点,点C是MB的中点,则AC的最小值是_____.
1.5
B
y
x
O
A
P
C
M
N
M
C
y
x
O
B
A
P
C
M
M
C
提升能力
强化训练
“瓜豆”模型
种圆得圆
5.如图,在等腰Rt△ABC中,∠BAC=90 ,AB=3,点D在BC上,以AD为边向右作正方形ADEF,连接BF,若∠FBC=30 ,则BD=____.
6.如图,等边△ABC的边长为8,点D为AB边上一动点,DE始终平行于BC,MN为△ADE的中位线,现将点D开始沿AB方向移动,移动到点B处停止,在整个移动过程中线段MN扫过的面积是_____.
△ABD≌△ACF,BD=FC
A
F
E
C
D
B
6
提升能力
强化训练
“瓜豆”模型
A
M
D
E
C
B
N
4 3
7.如图,△ABC是边长为4的等边三角形,AD为BC边上的高,点E为线段AD上一动点,连接EF,CE,将CE绕点C逆时针旋转60 得到线段CF,连接DF.△CEF的周长的最小值为____,DF的最小值是_____.
G
A
D
E
F
C
B
1
6
【方法一】连接BF,可得△CFB≌△CAE,
∴∠CBF=∠CAE=30 ,∴点F在射线BF上,
当DF⊥BF时,DF最短,
【方法二】取AC的中点G,连接EG,
可得△CFD≌△CEG,∴DF=EG,由垂线段最短得:
当GE⊥AD时GE最短,即DF最短。
提升能力
强化训练
“瓜豆”模型
8.如图,在等边△ABC中,AB=10,BD=4,BE=2,点P从点E出发沿EA方向运动,连结PD,以PD为边,在PD的右侧按如图所示的方式作等边△DPF,当点P从点E运动到点A时,点F运动的路径长是____.
【分析】根据△DPF是等边三角形,所以可知F点运动路径长与P点相同,P从E点运动到A点路径长为8,故此题答案为8.
A
D
F
P
E
C
B
8
提升能力
强化训练
“瓜豆”模型
同课章节目录
