专题5.2相似---A字形及其变形-中考数学二轮复习必会几何模型剖析(全国通用)
文档属性
| 名称 | 专题5.2相似---A字形及其变形-中考数学二轮复习必会几何模型剖析(全国通用) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-25 00:00:00 | ||
图片预览






文档简介
(共15张PPT)
专题五 与相似有关的模型
人教版中考第二轮总复习---几何模型
§5.2 “A字形”及其变形
考点归纳
模型分析
相似的基本模型
相似三角形是几何中重要的证明模型之一,是全等三角形的推广,分析图形间的关系离不开数量的计算.相似和勾股是产生等式的主要依据(其他依据还有面积法,三角函数等),因此要掌握相似三角形的基本图形,体会其各种 演变和联系.现将基本模型总结如下:
模型一 A字形; 模型二 X(8)字形; 模型三 K字形。
对于“A字形”及“ X字形”(或作平行线或其他辅助线去构造“AX字形”)问题,一般利用平行线分线段成比例定理或相似三角形的判定、性质去进行比例变形、等量代换,寻找中间比,从而将问题解决.
【例1】如图,点D,F在△ABC边AC上,点E在边BC上,且DE∥AB,CD2=CF·CA.
(1)求证:EF∥BD.
(2)如果AC·CF=BC·CE,求证:BD2=DE·BA
考点5-1
典例精讲
正“A字形”相似
C
D
B
A
E
F
∴BD2=BA·DE.
证明:(1)∵DE∥AB,
∴CD:AC=CE:CB.
∵CD2=CF·CA,
∴CD:AC=CF:CD.
∴CF:CD=CE:CB.
∴EF∥BD.
(2)∵EF∥BD,
∴∠CEF=∠CBD.
∵AC·CF=BC·CE,
∴AC:BC=CE:CF
∵∠C=∠C,
∴△CEF∽△CAB.
∴∠CEF=∠A.
∴∠DBE=∠A.
∵DE∥AB,
∴∠EDB=∠DBA.∠DBE=∠A,
∴△BAD∽△DBE.
∴BA:BD=BD:DE.
【例2】如图,在△ABC中,点D,E分别在边AB,AC上,∠AED=∠B,线段AG分别交线段DE,BC于点F,G,且AD:AC=DF:CG,
(1)求证:△ADF∽△ACG. (2)若AD:AC=3:7,求AF:FG的值.
考点5-2
典例精讲
斜“A字形”相似
A
D
C
B
E
G
(1)证明:∵∠AED=∠B,∠DAE=∠CAB,
∴△AED∽△ABC
∴∠ADF=∠C.
∵AD:AC=DF:CG
∴△ADF∽△ACG.
(2)解:∵△ADF∽△ACG,
∴AD:AC=AF:AG
∵AD:AC=3:7.
∴AF:AG=3:7.
∴AF:FG=3:4.
【例3】如图,在△ABC中,D为BC边上一点,BC=3BD,∠BAD=∠C.
求证:AC=AD.
考点5-3
典例精讲
“母子形”相似
A
D
C
B
证明:∵∠BAD=∠C,∠B=∠B,
∴△BAD∽△BCA.
∵BC=3BD,
∴ =
BA
BC
BD
BA
=
AD
AC
∴BA= BD.
3
∴AC= AD.
3
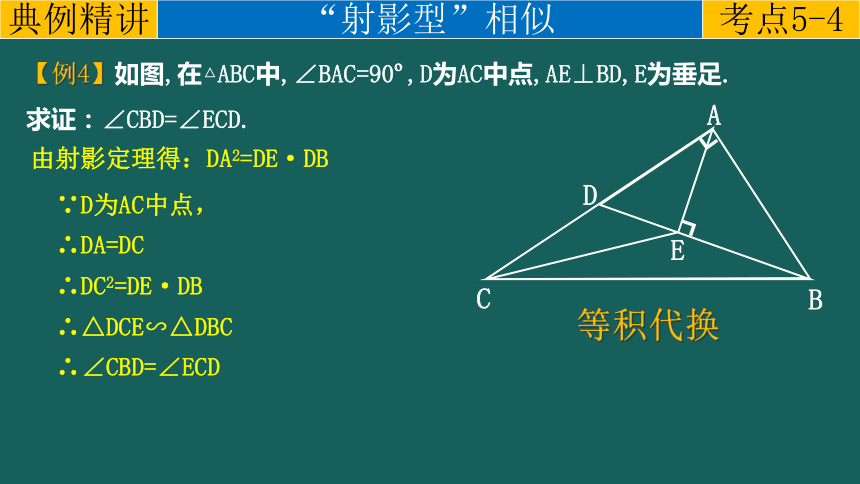
【例4】如图,在△ABC中,∠BAC=90 ,D为AC中点,AE⊥BD,E为垂足.
求证:∠CBD=∠ECD.
考点5-4
典例精讲
“射影型”相似
A
E
D
B
C
由射影定理得:DA2=DE·DB
等积代换
∵D为AC中点,
∴DA=DC
∴DC2=DE·DB
∴△DCE∽△DBC
∴∠CBD=∠ECD
【例5】如图,E是四边形ABCD的对角线BD上一点,且,∠EAB=∠DAC,
求证:∠EAD=∠BDC.
考点5-5
典例精讲
“旋转形”相似
∵∠AEB=∠EAD+∠ADE,∠ADC=∠BDC+∠ADE
∵∠EAB=∠DAC,
∴△ABE∽△ACD
∴∠AEB=∠ADC
∴∠EAD=∠BDC
A
E
D
C
B
证明:
∵ = .
AB
AE
AC
AD
∴ =
AB
AC
AE
AD
知识梳理
课堂小结
“A字形”及其变形
类别 正A型 斜A型 母子型 射影型 旋转型
图形
条件
结论
A
C
B
E
D
A
C
B
D
A
C
B
E
D
DE∥BC
∠AED=∠B
∠ACD=∠B
△ADE∽△ABC
△ADE∽△ACB
△ADC∽△ACB
(斜射影)
AC2=AD·AB
A
C
B
D
CD⊥AB,AC⊥BC
BC2=BD·BA.
△CAD∽△BCD∽△BAC
AC2=AD·AB;
△ABC∽△ADE
CD2=AD·BD;
B
D
A
E
C
A
C
E
D
B
④△BAD∽△CAE
②∠BAC=∠DAE
③∠BAD=∠CAE
① =
AB
AD
AC
AE
查漏补缺
针对训练
“A字形”及其变形
1.如图,在△ABC中,D为AB边上一点,且∠BCD=∠A,已知BC=2,AB=3,则BD=_____.
2.如图,D是△ABC的边BC上一点,AB=4,AD=2,∠DAC=∠B,如果△ABD的面积为15,那么△ACD的面积为_____.
3.如图,△ABC中,∠A=∠DBC,BC=,SΔBCD∶SΔABC=2:3,则CD=_____.
A
D
C
B
A
D
C
B
5
C
D
B
A
8
3
2 3
3
查漏补缺
针对训练
“A字形”及其变形
4.如图,⊙A是△ABC的外接圆,已知AD平分∠BAC交⊙O于点D,交BC边于点E,AD=5,BD=2,则DE的长为_____.
5.如图,将弧BC沿弦BC折叠,交直径AB于点D,若AD=4,DB=5,则BC的长是___
6.如图,在Rt△ABC中,∠ABC=90 ,BD⊥AC于D.若AB=6,AD=2,则AC=____.
7.如图,D是△ABC一边BC上一点,连接AD,使△ABC∽△DBA的条件是( )
A.AC:BC=AD:BD B.AC:BC=AB:AD C.AB2 =CD·BC D.AB2 =BD·BC
O
A
D
C
B
E
H
A
C
D
B
18
D
B
C
A
3 7
4
5
D
A
B
C
D
8.如图,在△ABC中,∠C的平分线交AB于D,过点D作DE∥BC交AC于E,若AD:DB=3:2,则EC:BC=_____.
9.如图,已知菱形ABCD内接于△AEF,AE=5cm,AF=4cm,则菱形的边长为_____.
10.在△ABC中,AB=6,AC=5,点D在边AB上,且AD=2,点E在边AC上,当AE=_____时,以A、D、E为顶点的三角形与△ABC相似.
11.如图,已知△ABC中,D为边AC上一点,P为边AB上一点,AB=12,AC=8,AD=6,当AP的长度为______时,△ADP和△ABC相似.
3:5
B
D
C
E
A
20/9
B
C
A
D
E
F
A
E
D
C
B
A
B
C
D
4或9
P2
P1
12
5
5
3
或
查漏补缺
针对训练
“A字形”及其变形
查漏补缺
针对训练
“A字形”及其变形
12.如图所示,在Rt△ACB中,ACB=90 ,CAB=30 ,点D是△ACB内一点,满足CD=1,BD=,AD=,求∠ADC的度数.
【分析】在Rt△ACB中,∠ACB=90 ,∠CAB=30 .
A
D
B
C
F
∴∠ADC=∠AFB=60 +90 =150 .
∴△ACD∽△ABF.
连接DF,∴Rt△ACB∽Rt△ADF
在根据勾股定理逆定理可证:△BDF为直角三角形且∠DFB=90 ,
解:将△ACD绕点A逆时针旋转30 ,再放 倍,得到△ABF,
2
3
∴BF= ,AF=
2
3
2 5
3
∴DF:AD:AF=1: 3:2且△AFD=60 ,
∵AD= 5,
∴DF=
5
3
∴BC:AC:AB=1: 3:2.将分散的条件通过旋转集中起来.
查漏补缺
针对训练
“A字形”及其变形
解:
即
7.如图,在△ABC与△ADE中,∠ACB=∠AED=90 ,∠ABC=∠ADE,连接BD,CE.若AC:BC=3:4,求BD:CE的值.
又
B
E
D
A
C
查漏补缺
针对训练
“A字形”及其变形
8.如图,在△ABC中,点D,E分别在边BC,AC上,点F在DE的延长线上,AD=AF,AE·CE=DE·EF.
(1)求证:△ADE∽△ACD.(2)若AE·BD=EF·AF,求证:AB=AC.
A
E
F
C
D
B
(1)证明:
又
又
(2)
13.已知△ABC中,∠AEF=∠ACB,
求证:(1)AE·AB=AF·AC;
(2)∠BED=∠CFD,∠EBD=∠FCD;
(3)∠DEF=∠DBC,∠DFE=∠DCB.
A
D
F
E
C
B
“A”字型相似
查漏补缺
针对训练
“A字形”及其变形
专题五 与相似有关的模型
人教版中考第二轮总复习---几何模型
§5.2 “A字形”及其变形
考点归纳
模型分析
相似的基本模型
相似三角形是几何中重要的证明模型之一,是全等三角形的推广,分析图形间的关系离不开数量的计算.相似和勾股是产生等式的主要依据(其他依据还有面积法,三角函数等),因此要掌握相似三角形的基本图形,体会其各种 演变和联系.现将基本模型总结如下:
模型一 A字形; 模型二 X(8)字形; 模型三 K字形。
对于“A字形”及“ X字形”(或作平行线或其他辅助线去构造“AX字形”)问题,一般利用平行线分线段成比例定理或相似三角形的判定、性质去进行比例变形、等量代换,寻找中间比,从而将问题解决.
【例1】如图,点D,F在△ABC边AC上,点E在边BC上,且DE∥AB,CD2=CF·CA.
(1)求证:EF∥BD.
(2)如果AC·CF=BC·CE,求证:BD2=DE·BA
考点5-1
典例精讲
正“A字形”相似
C
D
B
A
E
F
∴BD2=BA·DE.
证明:(1)∵DE∥AB,
∴CD:AC=CE:CB.
∵CD2=CF·CA,
∴CD:AC=CF:CD.
∴CF:CD=CE:CB.
∴EF∥BD.
(2)∵EF∥BD,
∴∠CEF=∠CBD.
∵AC·CF=BC·CE,
∴AC:BC=CE:CF
∵∠C=∠C,
∴△CEF∽△CAB.
∴∠CEF=∠A.
∴∠DBE=∠A.
∵DE∥AB,
∴∠EDB=∠DBA.∠DBE=∠A,
∴△BAD∽△DBE.
∴BA:BD=BD:DE.
【例2】如图,在△ABC中,点D,E分别在边AB,AC上,∠AED=∠B,线段AG分别交线段DE,BC于点F,G,且AD:AC=DF:CG,
(1)求证:△ADF∽△ACG. (2)若AD:AC=3:7,求AF:FG的值.
考点5-2
典例精讲
斜“A字形”相似
A
D
C
B
E
G
(1)证明:∵∠AED=∠B,∠DAE=∠CAB,
∴△AED∽△ABC
∴∠ADF=∠C.
∵AD:AC=DF:CG
∴△ADF∽△ACG.
(2)解:∵△ADF∽△ACG,
∴AD:AC=AF:AG
∵AD:AC=3:7.
∴AF:AG=3:7.
∴AF:FG=3:4.
【例3】如图,在△ABC中,D为BC边上一点,BC=3BD,∠BAD=∠C.
求证:AC=AD.
考点5-3
典例精讲
“母子形”相似
A
D
C
B
证明:∵∠BAD=∠C,∠B=∠B,
∴△BAD∽△BCA.
∵BC=3BD,
∴ =
BA
BC
BD
BA
=
AD
AC
∴BA= BD.
3
∴AC= AD.
3
【例4】如图,在△ABC中,∠BAC=90 ,D为AC中点,AE⊥BD,E为垂足.
求证:∠CBD=∠ECD.
考点5-4
典例精讲
“射影型”相似
A
E
D
B
C
由射影定理得:DA2=DE·DB
等积代换
∵D为AC中点,
∴DA=DC
∴DC2=DE·DB
∴△DCE∽△DBC
∴∠CBD=∠ECD
【例5】如图,E是四边形ABCD的对角线BD上一点,且,∠EAB=∠DAC,
求证:∠EAD=∠BDC.
考点5-5
典例精讲
“旋转形”相似
∵∠AEB=∠EAD+∠ADE,∠ADC=∠BDC+∠ADE
∵∠EAB=∠DAC,
∴△ABE∽△ACD
∴∠AEB=∠ADC
∴∠EAD=∠BDC
A
E
D
C
B
证明:
∵ = .
AB
AE
AC
AD
∴ =
AB
AC
AE
AD
知识梳理
课堂小结
“A字形”及其变形
类别 正A型 斜A型 母子型 射影型 旋转型
图形
条件
结论
A
C
B
E
D
A
C
B
D
A
C
B
E
D
DE∥BC
∠AED=∠B
∠ACD=∠B
△ADE∽△ABC
△ADE∽△ACB
△ADC∽△ACB
(斜射影)
AC2=AD·AB
A
C
B
D
CD⊥AB,AC⊥BC
BC2=BD·BA.
△CAD∽△BCD∽△BAC
AC2=AD·AB;
△ABC∽△ADE
CD2=AD·BD;
B
D
A
E
C
A
C
E
D
B
④△BAD∽△CAE
②∠BAC=∠DAE
③∠BAD=∠CAE
① =
AB
AD
AC
AE
查漏补缺
针对训练
“A字形”及其变形
1.如图,在△ABC中,D为AB边上一点,且∠BCD=∠A,已知BC=2,AB=3,则BD=_____.
2.如图,D是△ABC的边BC上一点,AB=4,AD=2,∠DAC=∠B,如果△ABD的面积为15,那么△ACD的面积为_____.
3.如图,△ABC中,∠A=∠DBC,BC=,SΔBCD∶SΔABC=2:3,则CD=_____.
A
D
C
B
A
D
C
B
5
C
D
B
A
8
3
2 3
3
查漏补缺
针对训练
“A字形”及其变形
4.如图,⊙A是△ABC的外接圆,已知AD平分∠BAC交⊙O于点D,交BC边于点E,AD=5,BD=2,则DE的长为_____.
5.如图,将弧BC沿弦BC折叠,交直径AB于点D,若AD=4,DB=5,则BC的长是___
6.如图,在Rt△ABC中,∠ABC=90 ,BD⊥AC于D.若AB=6,AD=2,则AC=____.
7.如图,D是△ABC一边BC上一点,连接AD,使△ABC∽△DBA的条件是( )
A.AC:BC=AD:BD B.AC:BC=AB:AD C.AB2 =CD·BC D.AB2 =BD·BC
O
A
D
C
B
E
H
A
C
D
B
18
D
B
C
A
3 7
4
5
D
A
B
C
D
8.如图,在△ABC中,∠C的平分线交AB于D,过点D作DE∥BC交AC于E,若AD:DB=3:2,则EC:BC=_____.
9.如图,已知菱形ABCD内接于△AEF,AE=5cm,AF=4cm,则菱形的边长为_____.
10.在△ABC中,AB=6,AC=5,点D在边AB上,且AD=2,点E在边AC上,当AE=_____时,以A、D、E为顶点的三角形与△ABC相似.
11.如图,已知△ABC中,D为边AC上一点,P为边AB上一点,AB=12,AC=8,AD=6,当AP的长度为______时,△ADP和△ABC相似.
3:5
B
D
C
E
A
20/9
B
C
A
D
E
F
A
E
D
C
B
A
B
C
D
4或9
P2
P1
12
5
5
3
或
查漏补缺
针对训练
“A字形”及其变形
查漏补缺
针对训练
“A字形”及其变形
12.如图所示,在Rt△ACB中,ACB=90 ,CAB=30 ,点D是△ACB内一点,满足CD=1,BD=,AD=,求∠ADC的度数.
【分析】在Rt△ACB中,∠ACB=90 ,∠CAB=30 .
A
D
B
C
F
∴∠ADC=∠AFB=60 +90 =150 .
∴△ACD∽△ABF.
连接DF,∴Rt△ACB∽Rt△ADF
在根据勾股定理逆定理可证:△BDF为直角三角形且∠DFB=90 ,
解:将△ACD绕点A逆时针旋转30 ,再放 倍,得到△ABF,
2
3
∴BF= ,AF=
2
3
2 5
3
∴DF:AD:AF=1: 3:2且△AFD=60 ,
∵AD= 5,
∴DF=
5
3
∴BC:AC:AB=1: 3:2.将分散的条件通过旋转集中起来.
查漏补缺
针对训练
“A字形”及其变形
解:
即
7.如图,在△ABC与△ADE中,∠ACB=∠AED=90 ,∠ABC=∠ADE,连接BD,CE.若AC:BC=3:4,求BD:CE的值.
又
B
E
D
A
C
查漏补缺
针对训练
“A字形”及其变形
8.如图,在△ABC中,点D,E分别在边BC,AC上,点F在DE的延长线上,AD=AF,AE·CE=DE·EF.
(1)求证:△ADE∽△ACD.(2)若AE·BD=EF·AF,求证:AB=AC.
A
E
F
C
D
B
(1)证明:
又
又
(2)
13.已知△ABC中,∠AEF=∠ACB,
求证:(1)AE·AB=AF·AC;
(2)∠BED=∠CFD,∠EBD=∠FCD;
(3)∠DEF=∠DBC,∠DFE=∠DCB.
A
D
F
E
C
B
“A”字型相似
查漏补缺
针对训练
“A字形”及其变形
同课章节目录
