专题5.1相似---比例式或乘积式的证明技巧-中考数学二轮复习必会几何模型剖析(全国通用)
文档属性
| 名称 | 专题5.1相似---比例式或乘积式的证明技巧-中考数学二轮复习必会几何模型剖析(全国通用) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-26 08:49:40 | ||
图片预览






文档简介
(共26张PPT)
专题五 与相似有关的模型
人教版中考第二轮总复习---几何模型
§5.1 比例式或乘积式的证明技巧
考点归纳
知识梳理
题型概述
通过前面的学习,我们知道,比例线段的证明,离不开“平行线模型”(A型、X型、K型等),也离不开下面的6种“相似模型”.
“模型”只是工具,怎样选择工具,怎样使用工具,取决于我们如何思考问题.合理的思维方法,能让模型成为解题的利刃,让复杂的问题变简单.
【技巧一】三点定型法
【技巧二】等长代换法
【技巧三】等比代换法
【技巧四】等积代换法
【例1】如图,平行四边形ABCD中,E是AB延长线上的一点,DE交BC于F.
求证:
A
D
C
F
E
B
三点:C、D、F;
三点:A、D、E。
技巧4-1
典例精讲
三点定型
DC
AE
=
CF
AD
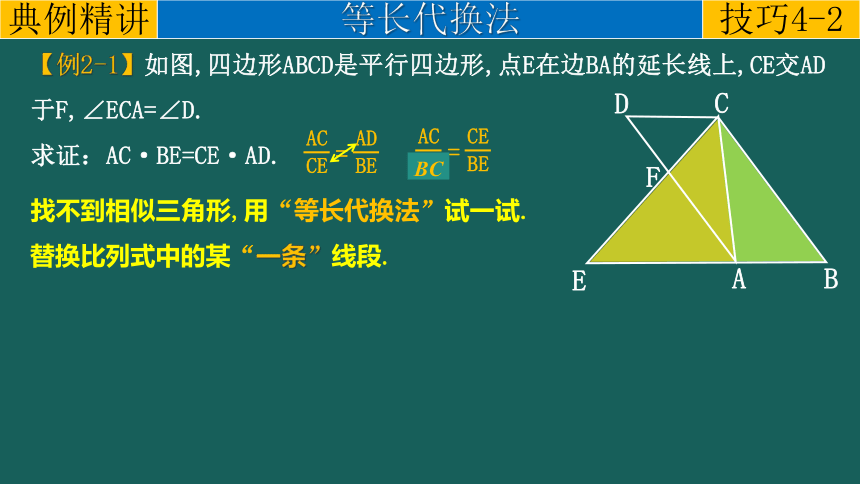
【例2-1】如图,四边形ABCD是平行四边形,点E在边BA的延长线上,CE交AD于F,∠ECA=∠D.
求证:AC·BE=CE·AD.
替换比列式中的某“一条”线段.
A
F
D
C
E
B
技巧4-2
典例精讲
等长代换法
找不到相似三角形,用“等长代换法”试一试.
AC
AD
=
CE
BE
BC
AC
CE
=
AD
BE
FC
FD
=
FB
FD
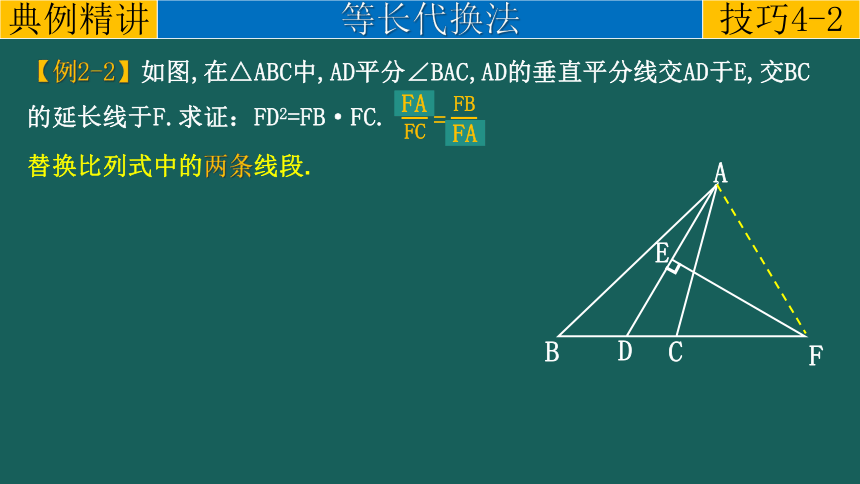
【例2-2】如图,在△ABC中,AD平分∠BAC,AD的垂直平分线交AD于E,交BC的延长线于F.求证:FD2=FB·FC.
替换比列式中的两条线段.
A
E
F
C
D
B
FA
技巧4-2
典例精讲
等长代换法
FA
【例3】如图,已知AB∥CD,AC、BD相交于点O.
求证:OA PD=OC PA
AB∥CD
A
O
B
C
D
P
△PAB∽△PDC
△AOB∽△COD
OA PD=OC PA
技巧4-3
典例精讲
等比代换法
两次运用平行线中的A型或X型找中间比
OA
OC
=
PA
PD
(本题的中间比是: )
AB
CD
PA
PD
=
AB
CD
OA
OC
=
AB
CD
OA
OC
=
PA
PD
E
F
求证:AE=BE
结论:两腰延长线的交点,对角线的交点,上下两底的中点,四点共线.
【例4】如图,在△ABC中,AD⊥BC于点D,DE⊥AB于点E,DF⊥AC于点F,
求证:AE·AB=AF·AC
A
F
C
D
B
E
技巧4-4
典例精讲
等积代换法
AE
AC
=
AF
AB
三点:A、E、F;
三点:A、B、C.
方法二:由射影定理得:AD2=AE·AB;AD2=AF·AC.
(本题的中间积是:AD2)
知识梳理
课堂小结
相似三角形的五大证明技巧
比例线段的证明,离不开“平行线模型”(K型、A型、X型等),也离不开6种“相似模型”。
本节课我们学习了相似三角形的5大证明技巧中的哪3种?
我们学习了
①三点定型法;
②等长代换法;
③等比代换法;
④等积代换法.
“模型”只是工具,怎样选择工具,怎样使用工具,取决于我们如何思考问题.合理的思维方法,能让模型成为解题的利刃,让复杂的问题变简单。
技巧5-1
针对训练
三点定型
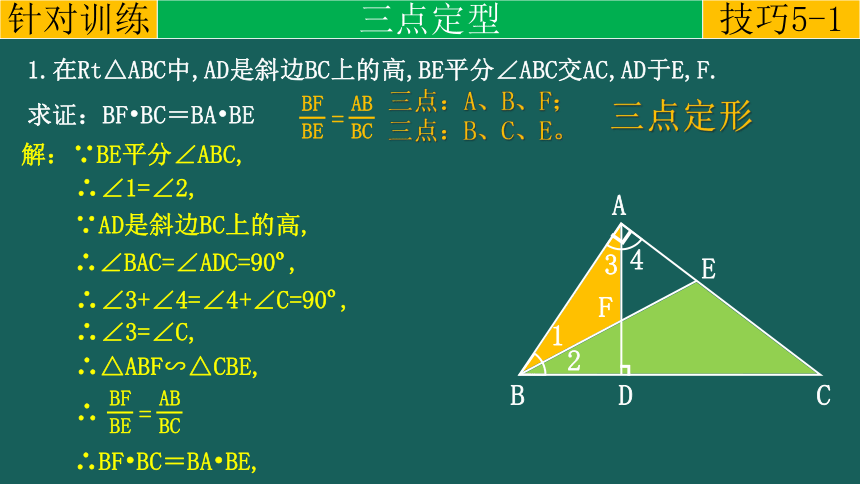
1.在Rt△ABC中,AD是斜边BC上的高,BE平分∠ABC交AC,AD于E,F.
求证:BF BC=BA BE
A
F
E
C
D
B
三点:A、B、F;
三点:B、C、E。
解:∵BE平分∠ABC,
∴∠1=∠2,
1
2
∵AD是斜边BC上的高,
∴∠BAC=∠ADC=90 ,
3
4
∴∠3+∠4=∠4+∠C=90 ,
∴∠3=∠C,
∴△ABF∽△CBE,
∴BF BC=BA BE,
三点定形
BF
BE
=
AB
BC
∴
BF
BE
=
AB
BC
D
E
A
M
C
B
证明:∵∠BAC=90 ,M为BC的中点.
∴AM∶MD=ME∶AM
1.如图,△ABC中,∠BAC=90 ,M为BC的中点,DM⊥BC交CA的延长线于D,交AB于E,求证:AM2=MD·ME.
∵∠BAC=90 ,DM⊥BC
∴MA=MB
∴∠B=∠1
∴∠D=∠B=90 -∠C
∴∠1=∠D
∵∠2=∠2
∴△EAM∽△ADM
∴AM2=MD·ME
三点:A、M、E;
三点:A、M、D。
三点定型
AM
MD
=
ME
AM
1
2
技巧5-1
针对训练
三点定型
技巧5-2
针对训练
等长代换法
2.如图,在菱形ABCD中,∠ABC=60 ,E是射线CB上一点,F是边CD上一点,且∠EAF=120 .求证:.
AC
替换比列式中的某“一条”线段.
A
F
D
C
B
E
3.如图,△ABC中,AB=AC,AD是中线,P是AD上一点,过C作CF∥AB,延长BP交AC于E,交CF于F.求证:BP2=PE·PF.
证明:连接PC
∴PC2=PE·PF
∴∠3=∠F
∵AB=AC,AD是中线
∴AD垂直平分BC
∴BP=CP
∴∠1=∠2
∵AB=AC
∴∠1+∠3=∠2+∠4
∴∠3=∠4
∵CF∥AB
∴∠4=∠F
∵∠CPE是△CPE和△FPC的公共角
∴△CPE∽△FPC
∴PE∶PC=PC∶PF
∴BP2=PE·PF
技巧5-2
针对训练
等长代换法
BP
PF
=
PE
BP
CP
CP
A
E
F
P
D
C
B
3
1
4
2
2.(1)如图1,△ABC中,AD平分∠BAC,EF垂直平分AD,交BC的延长线于点F,
求证:DF2=BF·CF
(2)△ABC中,AB=AC,AD是BC边上的中线,CF∥BA,BF交AD于点P,交AC于点E,
求证:BP2=PE·PF
A
P
E
F
C
D
B
图1
A
E
F
C
D
B
图2
等长代换法
技巧5-2
针对训练
等长代换法
4.如图,在△ABC中,点D,E在边BC上,且△ADE是等边三角形,∠BAC=120 ,
求证:DE2=BD·CE.
A
C
E
D
B
替换比列式中的两条线段.
DE
CE
=
BD
DE
AD
AE
技巧5-2
针对训练
等长代换法
A
G
C
B
E
F
D
技巧5-3
针对训练
等比代换法
4.如图,在△ABC中,点D在BC边上,连接AD,点G在AD上,GE∥BD,交AB于点E,
GF∥AC,交CD于点F,求证:.
(本题的中间比是: )
AG
DG
技巧5-3
针对训练
等比代换法
G
F
P
B
A
D
C
E
H
5.如图,在□ABCD的对角线BD上任取一点P,过点P引一直线分别与BA,DC两边的延长线交于E,G两点,又与BC,AD两边分别交于点F,H.
求证:.
DG∥BE,DG∥BE
证明:在□ABCD中.
(本题的中间比是: )
PB
PD
PE
PG
=
PB
PD
∴
;
PF
PH
=
PB
PD
.
PE
PG
=
PF
PH
∴
;
6.如图,在△ABC中,已知∠BAC=90 ,AD⊥BC于D,E为直角边AC的中点,过D、E作直线交AB的延长线于F.求证:AB·AF=AC·DF.
证明:∵∠A=90 ,AD⊥BC
∴△FBD∽△FDA
∴AB·AF=AC·DF.
∴△ABD∽△CAD
∴∠1=∠C=90 -∠ABC
∵∠BDA=∠ADC=90
∵AD⊥BC,E为直角边AC中点
∴DE=EC
∴∠3=∠C
∵∠3=∠2,∠1=∠C
∴∠1=∠2
∵∠F是△FBD与△FDA的公共角
两次运用相似找中间比
A
F
D
E
C
B
1
2
3
(本题的中间比是: )
BD
AD
AB
AC
=
BD
AD
∴
DF
AF
=
BD
AF
∴
AB
AC
=
DF
AF
∴
技巧5-3
针对训练
等比代换法
技巧5-4
针对训练
等积代换法
7.如图,在△ABC中,点D,E分别在BC和AC边上,点G是BE上一点,
且∠BAD=∠BGD=∠C.连接AG.
求证:.
A
G
B
D
E
C
(本题的中间积是:BD·BC)
8.如图,已知平行四边形ABCD中,E、F分别在直线AD、CD上,EF∥AC,BE、BF分别交AC于M、N.求证:AM=CN.
A
M
F
D
E
C
B
N
AD∥BC
AB∥CD
AC∥EF
∴AM=CN
技巧5-5
针对训练
证等量先证等比
AM
AC
=
EM
EB
CN
AC
=
FN
FB
CM
EB
=
FN
FB
AM
AC
=
CN
AC
3.(1)如图1,△ABC中,AD⊥BC于D,CE⊥AB于E,AD与CE相交干0点,
求证:0C·BD=AB·OD(2)如图2,∠ACB=90 ,FD垂直平分AB,交AC于点E,
求证:DC =DE·DF(遇平方,找有公共边的相似三角形)
A
C
B
D
F
E
图1
C
B
A
E
O
D
图2
等积代换法
提升能力
强化训练
比例式或乘积式的证明技巧
A
C
F
E
D
B
∴△BAF∽△BEA.
∴BD·BC=BF·BE
证明:∵∠BAC=90 ,AD⊥BC.
∴∠BAC=∠BDA=90 .
∵∠ABD=∠CBA.
∴△ABD∽△CBA.
∴AB2=BD·BC.
∵∠BAC=90 ,AF⊥BE.
∴∠BAC=∠AFB=90 .
∵∠FBA=∠ABE.
∴AB2=BF·BE.
等积代换法
提升能力
强化训练
比例式或乘积式的证明技巧
5.如图,Rt△ABC中,∠BAC=90 ,AD⊥BC于点D,E是AC上任意一点,连接BE,过点A作AF⊥BE于点F.求证:BD·BC=BF·BE.
AB
BD
=
BC
AB
∴
.
AB
BF
=
BE
BA
∴
.
6.如图,□ABCD中,过B作直线AC、AD于O、E,交CD的延长线于F,
求证:OB2=OE·OF.
A
E
O
D
F
C
B
AB∥CD
AD∥BC
OB2=OE·OF
等比代换
提升能力
强化训练
比例式或乘积式的证明技巧
OB
OF
=
OE
OB
OB
OF
=
OA
OC
OE
OB
=
OA
OC
OB
OF
=
OE
OB
(本题的中间比是: )
OA
OC
7.如图,在Rt△ABC中,∠BAC=90 ,AD⊥BC,P为AD的中点,EF⊥BC.
求证:EF2=AE·EC.
A
P
E
C
F
D
B
G
延长BA、FE交于点G,
△BAP∽△BGE
△BDP∽△BFE
∵AP=PD,∴GE=EF.
△AEG∽△FEC
EF2=AE·EC
等比代换
提升能力
强化训练
比例式或乘积式的证明技巧
(本题的中间比是: )
BP
BE
AP
EG
=
BP
BE
PD
EF
=
BP
BE
10.如图,在△ABC中(AB>AC)的边AB上取一点D,在边AC上取一点E,使AD=AE,直线DE和BC的延长线交于点P.
求证:BP·CE=CP·BD
A
D
E
P
C
B
F
过点B作BF∥AC交PD的延长线于点F.则BF=BD
△PBF∽△PCE
F
等长代换
替换比列式中的某一条线段.
提升能力
强化训练
比例式或乘积式的证明技巧
BP
CP
=
BD
CE
BF
BP
CP
=
BF
CE
8.如图,已知CE是Rt△ABC的斜边AB上的高,在EC的延长线上任取一点P,连接AP,BG⊥AP于点G,交CE于点D.求证:CE2=PE·DE.
P
G
C
B
E
A
D
由射影定理得:CE2=PE·DE
(本题的中间积是:AE·BE)
提升能力
强化训练
比例式或乘积式的证明技巧
等积代换
9.如图,在△ABC中,∠ACB=90 ,点D在边BC上,CE⊥AB,CF⊥AD,E,F分别是垂足,连接EF.求证:AE·BD=AD·EF.
A
F
D
C
E
B
(本题的中间积是:AC2)
提升能力
强化训练
比例式或乘积式的证明技巧
等积代换
专题五 与相似有关的模型
人教版中考第二轮总复习---几何模型
§5.1 比例式或乘积式的证明技巧
考点归纳
知识梳理
题型概述
通过前面的学习,我们知道,比例线段的证明,离不开“平行线模型”(A型、X型、K型等),也离不开下面的6种“相似模型”.
“模型”只是工具,怎样选择工具,怎样使用工具,取决于我们如何思考问题.合理的思维方法,能让模型成为解题的利刃,让复杂的问题变简单.
【技巧一】三点定型法
【技巧二】等长代换法
【技巧三】等比代换法
【技巧四】等积代换法
【例1】如图,平行四边形ABCD中,E是AB延长线上的一点,DE交BC于F.
求证:
A
D
C
F
E
B
三点:C、D、F;
三点:A、D、E。
技巧4-1
典例精讲
三点定型
DC
AE
=
CF
AD
【例2-1】如图,四边形ABCD是平行四边形,点E在边BA的延长线上,CE交AD于F,∠ECA=∠D.
求证:AC·BE=CE·AD.
替换比列式中的某“一条”线段.
A
F
D
C
E
B
技巧4-2
典例精讲
等长代换法
找不到相似三角形,用“等长代换法”试一试.
AC
AD
=
CE
BE
BC
AC
CE
=
AD
BE
FC
FD
=
FB
FD
【例2-2】如图,在△ABC中,AD平分∠BAC,AD的垂直平分线交AD于E,交BC的延长线于F.求证:FD2=FB·FC.
替换比列式中的两条线段.
A
E
F
C
D
B
FA
技巧4-2
典例精讲
等长代换法
FA
【例3】如图,已知AB∥CD,AC、BD相交于点O.
求证:OA PD=OC PA
AB∥CD
A
O
B
C
D
P
△PAB∽△PDC
△AOB∽△COD
OA PD=OC PA
技巧4-3
典例精讲
等比代换法
两次运用平行线中的A型或X型找中间比
OA
OC
=
PA
PD
(本题的中间比是: )
AB
CD
PA
PD
=
AB
CD
OA
OC
=
AB
CD
OA
OC
=
PA
PD
E
F
求证:AE=BE
结论:两腰延长线的交点,对角线的交点,上下两底的中点,四点共线.
【例4】如图,在△ABC中,AD⊥BC于点D,DE⊥AB于点E,DF⊥AC于点F,
求证:AE·AB=AF·AC
A
F
C
D
B
E
技巧4-4
典例精讲
等积代换法
AE
AC
=
AF
AB
三点:A、E、F;
三点:A、B、C.
方法二:由射影定理得:AD2=AE·AB;AD2=AF·AC.
(本题的中间积是:AD2)
知识梳理
课堂小结
相似三角形的五大证明技巧
比例线段的证明,离不开“平行线模型”(K型、A型、X型等),也离不开6种“相似模型”。
本节课我们学习了相似三角形的5大证明技巧中的哪3种?
我们学习了
①三点定型法;
②等长代换法;
③等比代换法;
④等积代换法.
“模型”只是工具,怎样选择工具,怎样使用工具,取决于我们如何思考问题.合理的思维方法,能让模型成为解题的利刃,让复杂的问题变简单。
技巧5-1
针对训练
三点定型
1.在Rt△ABC中,AD是斜边BC上的高,BE平分∠ABC交AC,AD于E,F.
求证:BF BC=BA BE
A
F
E
C
D
B
三点:A、B、F;
三点:B、C、E。
解:∵BE平分∠ABC,
∴∠1=∠2,
1
2
∵AD是斜边BC上的高,
∴∠BAC=∠ADC=90 ,
3
4
∴∠3+∠4=∠4+∠C=90 ,
∴∠3=∠C,
∴△ABF∽△CBE,
∴BF BC=BA BE,
三点定形
BF
BE
=
AB
BC
∴
BF
BE
=
AB
BC
D
E
A
M
C
B
证明:∵∠BAC=90 ,M为BC的中点.
∴AM∶MD=ME∶AM
1.如图,△ABC中,∠BAC=90 ,M为BC的中点,DM⊥BC交CA的延长线于D,交AB于E,求证:AM2=MD·ME.
∵∠BAC=90 ,DM⊥BC
∴MA=MB
∴∠B=∠1
∴∠D=∠B=90 -∠C
∴∠1=∠D
∵∠2=∠2
∴△EAM∽△ADM
∴AM2=MD·ME
三点:A、M、E;
三点:A、M、D。
三点定型
AM
MD
=
ME
AM
1
2
技巧5-1
针对训练
三点定型
技巧5-2
针对训练
等长代换法
2.如图,在菱形ABCD中,∠ABC=60 ,E是射线CB上一点,F是边CD上一点,且∠EAF=120 .求证:.
AC
替换比列式中的某“一条”线段.
A
F
D
C
B
E
3.如图,△ABC中,AB=AC,AD是中线,P是AD上一点,过C作CF∥AB,延长BP交AC于E,交CF于F.求证:BP2=PE·PF.
证明:连接PC
∴PC2=PE·PF
∴∠3=∠F
∵AB=AC,AD是中线
∴AD垂直平分BC
∴BP=CP
∴∠1=∠2
∵AB=AC
∴∠1+∠3=∠2+∠4
∴∠3=∠4
∵CF∥AB
∴∠4=∠F
∵∠CPE是△CPE和△FPC的公共角
∴△CPE∽△FPC
∴PE∶PC=PC∶PF
∴BP2=PE·PF
技巧5-2
针对训练
等长代换法
BP
PF
=
PE
BP
CP
CP
A
E
F
P
D
C
B
3
1
4
2
2.(1)如图1,△ABC中,AD平分∠BAC,EF垂直平分AD,交BC的延长线于点F,
求证:DF2=BF·CF
(2)△ABC中,AB=AC,AD是BC边上的中线,CF∥BA,BF交AD于点P,交AC于点E,
求证:BP2=PE·PF
A
P
E
F
C
D
B
图1
A
E
F
C
D
B
图2
等长代换法
技巧5-2
针对训练
等长代换法
4.如图,在△ABC中,点D,E在边BC上,且△ADE是等边三角形,∠BAC=120 ,
求证:DE2=BD·CE.
A
C
E
D
B
替换比列式中的两条线段.
DE
CE
=
BD
DE
AD
AE
技巧5-2
针对训练
等长代换法
A
G
C
B
E
F
D
技巧5-3
针对训练
等比代换法
4.如图,在△ABC中,点D在BC边上,连接AD,点G在AD上,GE∥BD,交AB于点E,
GF∥AC,交CD于点F,求证:.
(本题的中间比是: )
AG
DG
技巧5-3
针对训练
等比代换法
G
F
P
B
A
D
C
E
H
5.如图,在□ABCD的对角线BD上任取一点P,过点P引一直线分别与BA,DC两边的延长线交于E,G两点,又与BC,AD两边分别交于点F,H.
求证:.
DG∥BE,DG∥BE
证明:在□ABCD中.
(本题的中间比是: )
PB
PD
PE
PG
=
PB
PD
∴
;
PF
PH
=
PB
PD
.
PE
PG
=
PF
PH
∴
;
6.如图,在△ABC中,已知∠BAC=90 ,AD⊥BC于D,E为直角边AC的中点,过D、E作直线交AB的延长线于F.求证:AB·AF=AC·DF.
证明:∵∠A=90 ,AD⊥BC
∴△FBD∽△FDA
∴AB·AF=AC·DF.
∴△ABD∽△CAD
∴∠1=∠C=90 -∠ABC
∵∠BDA=∠ADC=90
∵AD⊥BC,E为直角边AC中点
∴DE=EC
∴∠3=∠C
∵∠3=∠2,∠1=∠C
∴∠1=∠2
∵∠F是△FBD与△FDA的公共角
两次运用相似找中间比
A
F
D
E
C
B
1
2
3
(本题的中间比是: )
BD
AD
AB
AC
=
BD
AD
∴
DF
AF
=
BD
AF
∴
AB
AC
=
DF
AF
∴
技巧5-3
针对训练
等比代换法
技巧5-4
针对训练
等积代换法
7.如图,在△ABC中,点D,E分别在BC和AC边上,点G是BE上一点,
且∠BAD=∠BGD=∠C.连接AG.
求证:.
A
G
B
D
E
C
(本题的中间积是:BD·BC)
8.如图,已知平行四边形ABCD中,E、F分别在直线AD、CD上,EF∥AC,BE、BF分别交AC于M、N.求证:AM=CN.
A
M
F
D
E
C
B
N
AD∥BC
AB∥CD
AC∥EF
∴AM=CN
技巧5-5
针对训练
证等量先证等比
AM
AC
=
EM
EB
CN
AC
=
FN
FB
CM
EB
=
FN
FB
AM
AC
=
CN
AC
3.(1)如图1,△ABC中,AD⊥BC于D,CE⊥AB于E,AD与CE相交干0点,
求证:0C·BD=AB·OD(2)如图2,∠ACB=90 ,FD垂直平分AB,交AC于点E,
求证:DC =DE·DF(遇平方,找有公共边的相似三角形)
A
C
B
D
F
E
图1
C
B
A
E
O
D
图2
等积代换法
提升能力
强化训练
比例式或乘积式的证明技巧
A
C
F
E
D
B
∴△BAF∽△BEA.
∴BD·BC=BF·BE
证明:∵∠BAC=90 ,AD⊥BC.
∴∠BAC=∠BDA=90 .
∵∠ABD=∠CBA.
∴△ABD∽△CBA.
∴AB2=BD·BC.
∵∠BAC=90 ,AF⊥BE.
∴∠BAC=∠AFB=90 .
∵∠FBA=∠ABE.
∴AB2=BF·BE.
等积代换法
提升能力
强化训练
比例式或乘积式的证明技巧
5.如图,Rt△ABC中,∠BAC=90 ,AD⊥BC于点D,E是AC上任意一点,连接BE,过点A作AF⊥BE于点F.求证:BD·BC=BF·BE.
AB
BD
=
BC
AB
∴
.
AB
BF
=
BE
BA
∴
.
6.如图,□ABCD中,过B作直线AC、AD于O、E,交CD的延长线于F,
求证:OB2=OE·OF.
A
E
O
D
F
C
B
AB∥CD
AD∥BC
OB2=OE·OF
等比代换
提升能力
强化训练
比例式或乘积式的证明技巧
OB
OF
=
OE
OB
OB
OF
=
OA
OC
OE
OB
=
OA
OC
OB
OF
=
OE
OB
(本题的中间比是: )
OA
OC
7.如图,在Rt△ABC中,∠BAC=90 ,AD⊥BC,P为AD的中点,EF⊥BC.
求证:EF2=AE·EC.
A
P
E
C
F
D
B
G
延长BA、FE交于点G,
△BAP∽△BGE
△BDP∽△BFE
∵AP=PD,∴GE=EF.
△AEG∽△FEC
EF2=AE·EC
等比代换
提升能力
强化训练
比例式或乘积式的证明技巧
(本题的中间比是: )
BP
BE
AP
EG
=
BP
BE
PD
EF
=
BP
BE
10.如图,在△ABC中(AB>AC)的边AB上取一点D,在边AC上取一点E,使AD=AE,直线DE和BC的延长线交于点P.
求证:BP·CE=CP·BD
A
D
E
P
C
B
F
过点B作BF∥AC交PD的延长线于点F.则BF=BD
△PBF∽△PCE
F
等长代换
替换比列式中的某一条线段.
提升能力
强化训练
比例式或乘积式的证明技巧
BP
CP
=
BD
CE
BF
BP
CP
=
BF
CE
8.如图,已知CE是Rt△ABC的斜边AB上的高,在EC的延长线上任取一点P,连接AP,BG⊥AP于点G,交CE于点D.求证:CE2=PE·DE.
P
G
C
B
E
A
D
由射影定理得:CE2=PE·DE
(本题的中间积是:AE·BE)
提升能力
强化训练
比例式或乘积式的证明技巧
等积代换
9.如图,在△ABC中,∠ACB=90 ,点D在边BC上,CE⊥AB,CF⊥AD,E,F分别是垂足,连接EF.求证:AE·BD=AD·EF.
A
F
D
C
E
B
(本题的中间积是:AC2)
提升能力
强化训练
比例式或乘积式的证明技巧
等积代换
同课章节目录
