专题5.4相似---K字形及其变形-中考数学二轮复习必会几何模型剖析(全国通用)
文档属性
| 名称 | 专题5.4相似---K字形及其变形-中考数学二轮复习必会几何模型剖析(全国通用) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-25 10:16:51 | ||
图片预览








文档简介
(共34张PPT)
专题五 与相似有关的模型
人教版中考第二轮总复习---几何模型
§5.4 “K字形”及其变形
考点归纳
模型分析
相似的基本模型
相似三角形是几何中重要的证明模型之一,是全等三角形的推广,分析图形间的关系离不开数量的计算.相似和勾股是产生等式的主要依据(其他依据还有面积法,三角函数等),因此要掌握相似三角形的基本图形,体会其各种 演变和联系.现将基本模型总结如下:
模型一 A字形; 模型二 X(8)字形; 模型三 K字形(一线三等角)。
对于“A字形”及“ X字形”(或作平行线或其他辅助线去构造“AX字形”)问题,一般利用平行线分线段成比例定理或相似三角形的判定、性质去进行比例变形、等量代换,寻找中间比,从而将问题解决.
考点3-1
典例精讲
K字形(一线三等角)
【例1】如图,△ACB为等腰直角三角形,点O是斜边AB的中点,∠EOF=45 .
⑴求证:△AOE∽△BFO;⑵若AB=4,求AE·BF的值.
A
C
B
O
F
E
3
2
1
⑴证明:∵△ACB为等腰直角三角形
∴△AOE∽△BFO.
∴∠A=∠B=45 ,∠3+∠2=135 .
∵∠EOF=45 .
∴∠1+∠2=135 .
∴∠3=∠1.
⑵解:∵△AOE∽△BFO.
∴AE BF=4
∴AE:BO=AO:BF.
∴AE BF=AO BO.
∵AO=BO=2.
∴△ABP∽△PCD.
【变式】如图,在△ABC中,AB=AC,点D、P分别在边AC、BC上,且∠APD=∠B.
求证:AC·CD=CP·BP.
证明:∵AB=AC,
∴∠B=∠C.
∵∠APD=∠B,
∴∠APD=∠C.
∵∠APC=∠B+∠BAP,∠APC=∠APD+∠CPD.
∴∠B+∠BAP=∠APD+∠CPD.
∴∠BAP=∠CPD.
∴
=
BP
CD
BA
CP
∵AB=AC.
∴AC·CD=CP·BP.
C
A
D
B
P
考点3-1
变式训练
K字形(一线三等角)
考点3-1
知识归纳
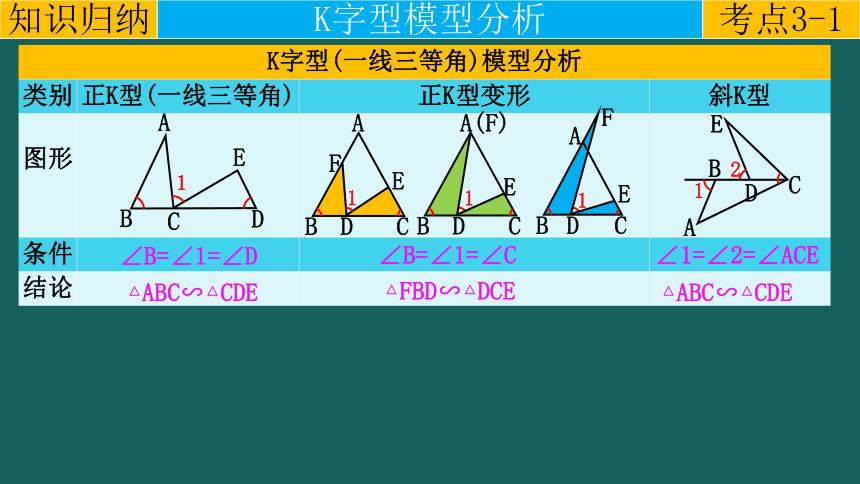
K字型模型分析
K字型(一线三等角)模型分析 类别 正K型(一线三等角) 正K型变形 斜K型
图形
条件
结论
∠B=∠1=∠D
△ABC∽△CDE
A
E
F
C
B
D
1
A(F)
E
C
B
D
1
A
E
C
B
D
1
F
B
C
D
E
A
1
∠B=∠1=∠C
△FBD∽△DCE
B
D
E
C
A
1
2
∠1=∠2=∠ACE
△ABC∽△CDE
【例2】如图,在正方形ABCD中,E是边AB上的一动点(不与点A、B重合),连接DE,点A关于直线DE的对称点为F,连接EF并延长交BC于点G,连接DG,过点E作EH⊥DE交DG的延长线于点H,连接BH.
(1)求证:GF=GC;(2)用等式表示线段BH与AE的数量关系,并证明.
D
H
B
E
C
A
F
G
解:(1)连接DF,
Q
∴△DEH是等腰直角三角形.
过点H作HQ⊥AB交AB延长线于点Q.
(2)BH= AE.
2
易证∠EDG= ∠ADC=45 .
1
2
易证△DAE≌△EQH.
∴AE=QH,DA=EQ.
∵AB=DA=EQ.
∴AE=BQ.
∴BQ=HQ.
∴△BQH是等腰直角三角形.
∴BH= HQ= AE.
2
2
易证△DGF≌△DGC,
易证△DAE≌△DFE,
∴GF=GC.
考点3-2
典例精讲
K字形(一线三直角)
Q
【变形一】由(1),(3)→(2)如图,E是正方形ABCD的边AB上一点,∠CBH=45 ,过点E作EH⊥DE交BH于点H,求证:∠EDH=45 .
(1)∠DEH=90 ;(2)∠EDH=45 ;(3)∠CBH=45 .
D
H
B
E
C
A
G
【分析】可以采用构造三垂直思路,但是对于△DAE和△EQH,并没有已知的相等线段,此路不通.
不同的条件下方法可能会不同,利用好题目的已知条件,比如此处∠CBH=45 如何运用
证明:在AD边上取点F使得AF=AE,连接EF.
∴∠DFE=135 =∠EBH,易证∠FDE=∠BEH,DF=EB,
∴△DFE≌△EBH,
∴DE=DH.
∴△DEH是等腰直角三角形,
∴∠DEH=45 .
考点3-2
变式训练
K字形(一线三直角)
(1)∠DEH=90 ;(2)∠EDH=45 ;(3)∠CBH=45 .
【变形二】由(2),(3)→(1)如图,E是正方形ABCD的边AB上一点,
∠EDH=∠CBH=45 ,求证:DE⊥EH.
∴∠DEH=∠DBH=90 .
D
H
B
E
C
A
G
O
证明:∵∠EDH=45 ,∠EBH=90 +45 =135 .
∴∠EDH+∠EBH=180 .
∴B、E、D、H四点共圆,连接BD.
∴DE⊥EH.
考点3-2
变式训练
K字形(一线三直角)
考点3-2
知识归纳
K字形(一线三直角)
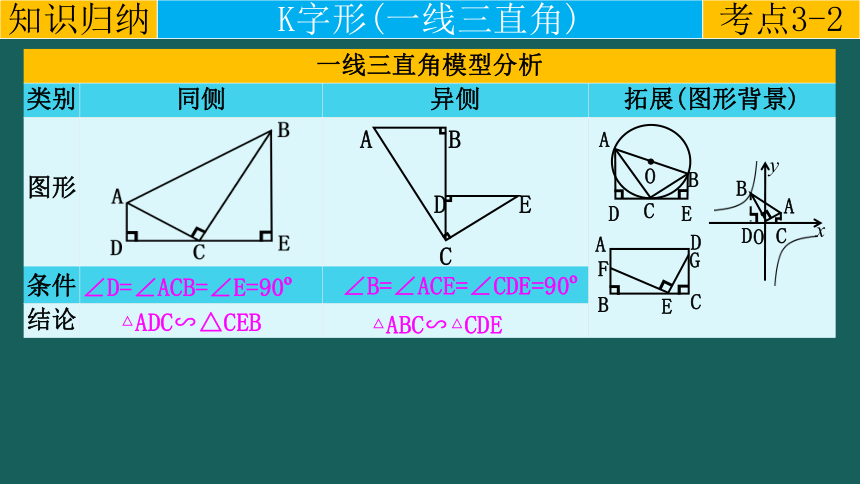
一线三直角模型分析 类别 同侧 异侧 拓展(图形背景)
图形
条件 结论 ∠D=∠ACB=∠E=90
△ADC∽△CEB
A
O
E
C
B
D
y
O
x
C
D
A
B
A
F
C
D
B
E
G
C
A
B
D
E
∠B=∠ACE=∠CDE=90
△ABC∽△CDE
y
O
x
B
A
考点3-3
典例精讲
构造一线三直角
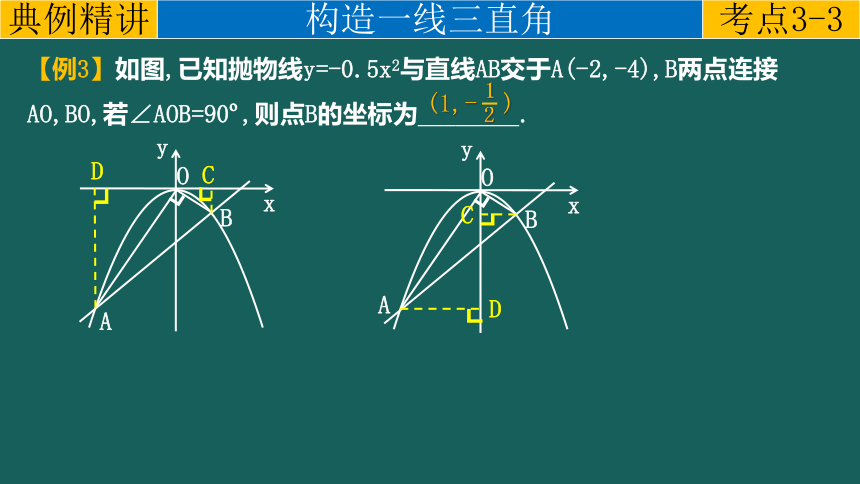
【例3】如图,已知抛物线y=-0.5x2与直线AB交于A(-2,-4),B两点连接AO,BO,若∠AOB=90 ,则点B的坐标为________.
C
D
(1,- )
1
2
y
O
x
B
A
C
D
如图,在平面直角坐标系中,等腰直角三角形OAB的一个顶点在原点处,∠ABO=90 ,OB=AB,已知点A(2,4),则点B的坐标为______.
y
x
B
A
O
(3,1)
E
F
N
M
考点3-3
变式训练
构造一线三直角
考点3-3
知识归纳
构造一线三直角
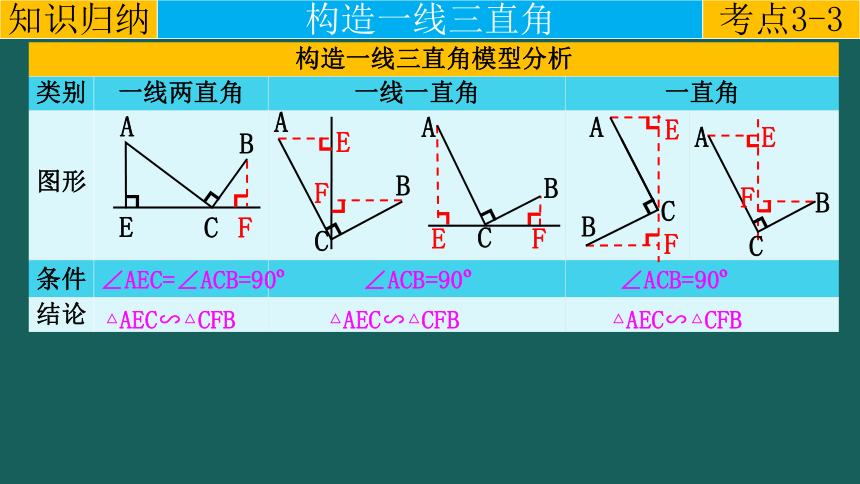
构造一线三直角模型分析 类别 一线两直角 一线一直角 一直角 图形
条件 结论 F
∠AEC=∠ACB=90
C
B
A
E
E
F
A
B
C
B
C
A
E
F
C
A
B
E
F
A
C
B
E
F
△AEC∽△CFB
∠ACB=90
△AEC∽△CFB
∠ACB=90
△AEC∽△CFB
知识梳理
课堂小结
K字形及其变形
模型说明
识别
方法
构造一线三直角的基本步骤
一线三等角
一线三直角是一个常见的相似模型,指的是有三个直角的顶点在同一条直线上构成的相似图形,也有称三垂直模型、K型图或M型图.
(一线三等角不仅可以是直角,也可以是锐角或钝角)
(1)找图中已知的直角,顺着这个直角的顶点寻找或者构造模型中的一线;
(2)构造其他直角,构造的直角的顶点必须在同一条直线上,这条直线可能在已知角的外部,也可能穿过这个角.
若出现一直角的顶点在一条直线上的形式,就可以构造两侧的直角三角形,利用全等三角形或相似三角形解决相关问题.本质就是找角、定线、构相似.
1.如图四边形ABCD、EFGH是正方形,NHMC是矩形,A,B,N,E,F五点在同一直线上,若正方形ABCD,EFGH的边长分别为3,4,BN=2,则NH为_____.
2.如图,四边形ACDF是正方形,∠CEA和∠ABF都是直角且点E,A,B三点共线,AB=4,则阴影部分的面积是____.
A
M
H
G
F
E
N
B
C
D
2 13
提升能力
强化训练
K字形及其变形
8
B
A
F
D
C
E
M
N
y
x
O
B
A
提升能力
强化训练
K字形及其变形
3.如图,点A是反比例函数y=-的图像上的一个动点,连接OA,若将线段0A绕点0顺时针旋转90 得到线段0B,则点B所在的反比例函数表达式为_____.
4.如图,在平面直角坐标系中,A(2,0),B(0,1),AC由AB绕点A顺时针旋转90 而得,则AC所在直线的解析式是_______.
5.如图,已知A(0,3),B(4,0),点C在第一象限,且AC=5,BC=10,则直线OC的函数表达式为_______.
2
x
y=
y=2x-4
D
y
O
x
C
B
A
H
y
x
O
C
A
B
y= x
4
5
提升能力
强化训练
K字形及其变形
6.如图,已知△ABC中∠ABC=90 ,AB=BC,△ABC三个顶点在相互平行的三条直线上,且l1与l2之间的距离为2,l2与l3之间的距离为3,则AC的长是_____.
7.如图,在平面直角坐标系中,矩形OABC的两边OA,OC分别在x轴,y轴上,且OA=8,OC=4.若把矩形OABC绕着点O逆时针旋转,使点A恰好落在BC边上的点A1处,则点B的对应点B1的坐标为______________.
E
D
l1
l3
l2
A
C
B
H
N
M
2 17
E
F
B
y
x
A
O
C
A1
C1
B1
H
M
( , )
4 3-2
2 3+4
提升能力
强化训练
K字形及其变形
8.如图,点A(0,8),点B(4,0),连接AB,点M、N分别是OA,AB的中点,在射线MN上有一动点P.若△ABP是直角三角形,则点P的坐标是__________________.
9.如图,在平面直角坐标系中,点C(0,4),射线CE∥x轴,直线y=-0.5x+b交线段OC于点B,交x轴于于点A,D是射线CE上一点,若存在点D,使得△ABD恰为等腰直角三角形,则b的值为___________.
y
x
A
M
B
O
N
P
P
H
P
H
(12,4)或( ,4)
2 5+2
y
O
x
C
E
A
B
D
y
O
x
C
E
A
B
D
y
O
x
C
E
A
B
D
H
H
4
3
8
3
或
或2
提升能力
强化训练
K字形及其变形
A
F
E
C
D
B
10.如图,正方形ABCD的边长为16,在BC边上取一动点E,连接AE,作EF⊥AE,交CD边于点F.若CF=3,求CE的长.
解:∵四边形ABCD为正方形.
∴∠B=∠C=90 .
∴∠BAE=∠AEB=90 .
∵EF⊥AE.
∴∠AEF=90 .
∴∠AEB+∠CEF=90 .
∴∠BAE=∠CEF.
∴△ABE∽△ECF.
∴
CE
BA
=
CF
BE
即:
CE
16
=
3
16-CE
∴CE=4或12.
提升能力
强化训练
K字形及其变形
11.如图,△ABC≌△DEF(点A,B分别与点D,E对应),AB=AC=5,BC=6,△ABC固定不动,△DEF运动,并满足点E在BC边从B向C移动(点E不与B,C重合),DE始终经过点A,EF与AC边交于点M,当△AEM是等腰三角形时,求BE的长.
A
M
C
E
B
F
D
解:∵∠AEF=∠B=∠C,且∠AME>∠C.
∴AE≠AM.
①当AE=EM时,则△ABE≌△ECM.
∴CE=AB=5.
∴BE=BC-CE=6-5=1.
②当AM=EM时,则∠MAE=∠MEA,
∴∠MAE+∠BAE=∠MEA+∠CEM.
∴∠MAB=∠CEA.
∵∠C=∠C,
∴△ABC∽△ECA
∴CE:AC=AC:CB
∴BE=BC-CE=
11
6
∴CE=
25
6
提升能力
强化训练
K字形及其变形
12.如图,在△ABC中,AB=AC,∠BAC=90 ,点D是边BC的中点,点E在边AB上(点E不与点A,B重合),点F在边AC上,连接DE,DF,∠EDF=45 .
求证:.
B
A
C
D
F
E
证明:∵∠BDF=∠BDE+∠EDF,∠BDE=∠C+∠CFD.
∴∠BDE+∠EDF=∠C+∠CFD.
∵∠C=∠EDF=45 .
∴∠BDE=∠CFD.
∴△BDE∽△CFD.
∴
BE
CD
=
BD
CF
=
DE
DF
∴
BE
CD
·
BD
CF
=( )2
DE
DF
∵BD=CD.
∴
BE
CF
DE2
DF2
=
13.如图,在菱形ABCD中,∠ABC=120 ,将菱形沿EF折叠,使点A恰好落在对角线BD上的点G处(不与B、D重合),若DG=2,BG=6,则BE的长为____.
A
G
D
C
F
E
B
易证△FGD∽△GEB
【分析】等边翻折得到一线三等角.
由题意可得:∠FDG=∠FGE=∠GBE=60 .
FG
GE
=
DG
EB
=
FD
GB
∴
设FG=x,则AE=x,DF=8-x,设GE=y,则AE=y,BE=8-y.
代入得:
x
y
=
2
8-y
=
8-x
6
解得:y=
26
5
∴BE=8- =
26
5
14
5
14
5
提升能力
强化训练
K字形及其变形
提升能力
强化训练
K字形及其变形
14.如图,在平面直线坐标系中,点M(2,1)是直线AB:y=x上一点,将直线AB绕点M顺时针旋转45 得到直线CD,求CD解析式.
y=- x+
5
3
1
3
y
O
x
B
A
C
M
D
45
E
P
F
P
E
F
y
O
x
B
A
C
M
D
45
提升能力
强化训练
K字形及其变形
【变式】如图,在平面直线坐标系中,点M(2,1)是直线AB:y=x上一点,将直线AB绕点M顺时针旋转α得到直线CD,且tanα=,求直线CD解析式.
y
O
x
B
A
C
M
D
α
E
P
F
y=- x+
15
7
4
7
提升能力
强化训练
K字型(一线三直角)
1.如图,∠BAD=∠ACB=90 ,AB=AD,AC=4BC,若CD=5,则S四边形ABCD=_____.
2.如图,已知∠ACB=90 ,AD=BC,CD=BE,AE与BD相交于点F,则∠AFD=____.
3.如图,在四边形ABCD中,AD=3,CD=4,∠ABC=∠ACB=∠ADC=45 ,则BD=____
A
D
C
B
10
E
A
F
E
D
C
B
G
G
45
F
E
A
O
B
C
D
34
提升能力
强化训练
K字型(一线三直角)
4.如图,在平面直角坐标系中,点A(0,2),点B(4,0),点C在第一象限内,若△ABC为等边三角形,则点C的坐标为________.
5.抛物线y=x2-4x+3与坐标轴交于A,B,C三点,点P在抛物线上,PE⊥BC于点E,若PE=2CE,则点P的坐标为_________.
y
x
C
B
A
O
F
E
D
2
3
y
O
x
B
A
C
E
P
M
N
3
3
m
m
2m
2m
(3m,3+m)
(5,3 3 )
( , )
13
3
40
9
21
3
2 3
3
7
提升能力
强化训练
K字型(一线三直角)
6.如图直角梯形ABCD中,AD//BC,AB⊥BC,AD=2,BC=3,将腰CD以D为中心逆时针旋转90°至ED,连AE、CE,则△ADE的面积是____.
1
N
M
A
E
D
C
B
提升能力
强化训练
K字型(一线三直角)
D
B
C
A
F
E
7.如图,正方形ABCD和Rt△AEF,AB=5,AE=AF=4,连接BF,DE.若△AEF绕点A旋转,当∠ABF最大时,S△ADE=___.
【分析】动态问题先分析何时∠ABF最大.F点轨迹是以点A为圆心,AF为半径的圆,当BF与圆相切时,∠ABF最大,分别过点E、F作直线DA的垂线,垂足分别记为M、N,
M
N
D
B
C
A
F
E
M
N
易证△AME≌△FNA,
∴EM=AN=4×3/5=12/5.
∴S△ADE=1/2×5×12/5=6.
6
提升能力
强化训练
K字型(一线三直角)
8.如图,在△ABC中,AB=AC=5,BC=4,D为边AB上一动点(B点除外),以CD为一边作正方形CDEF,连接BE,则△BDE面积的最大值为___.
【分析】求三角形的面积,可以首先考虑面积公式,以BD为底,需作高 分别过C、E作BA的垂线,垂足分别记为点M、N.
F
A
D
E
B
C
N
M
8
故△BDE面积的最大值为8.
易证△DMC≌△END,
由tan∠ABC=1/2得:CM=4,BM=8,
设BD=x,则EN=DM=8-x.
∴S△BDE=1/2x(8-x)=-1/2x2+4x.
当x=4时,S△BDE取到最大值8.
提升能力
强化训练
K字型(一线三直角)
9.如图,正方形ABCD的对角线AC上有一点E,且CE=4AE,点F在DC的延长线上,连接EF,过点E作EG⊥EF,交CB的延长线于点G,连接FG并延长,交4C的延长线于点P,若AB=5,CF=2,则线段EP的长是______.
N
M
P
B
F
C
G
A
D
E
P
B
F
C
G
A
D
E
H
【分析】有直角便可考虑构造三垂直.如下左图,过点E作EM⊥CD交CD于M点,过点G作GN⊥ME交ME延长线于点N,易证△FME≌△ENG,连接GA,点F作FH⊥AP交AP于H点,
易证△GAE∽△EHF,
∴△PHF∽△PAG.
∴FH:GA=PH:PA.
解得:PH=
3 2
2
∴PE=
13 2
2
提升能力
强化训练
K字型(一线三直角)
10.如图,点P为矩形ABCD的对角线BD上一点,PE⊥AP交BC于点E,若AD=10,
DC=6,求的值.
M
N
A
P
E
C
D
B
提升能力
强化训练
K字型(一线三直角)
11.如图,在四边形ABCD中,∠ABC=90 ,AB=3,BC=4,DA=5,求BD的长
H
A
D
C
B
提升能力
强化训练
K字型(一线三直角)
12.在△ABC中,∠ABC=90 ,tan∠BAC=.
(1)如图①,分别过A、C两点作经过点B的直线的垂线,垂足分别为点M、N.若点B恰好是线段MN的中点,求tan∠BAM的值;
(2)如图②,P是边BC的延长线上一点,∠APB=∠BAC,求tan∠PAC的值.
B
A
C
M
N
图①
D
E
A
C
P
B
图②
提升能力
强化训练
K字型(一线三直角)
13.两块三角板如图放置,已知∠BAC=∠ADC=90 ,∠ABC=45 ,∠ACD=30 ,
BC=cm.
(1)分别求线段AD,CD的长度;
(2)求BD2的值。
E
A
C
D
B
提升能力
强化训练
K字型(一线三直角)
14.如图,已知直线:y=-x+6分别与x轴、y轴交于点B,A,以AB为斜边向△OAB外作等腰直角△ABC,AC=BC.
(1)分别写出点A、B的坐标;
(2)求线段OC的长度。
y
O
x
B
A
C
F
E
(1)A(0,6),B(10,0)
(2)
M
N
8 2
专题五 与相似有关的模型
人教版中考第二轮总复习---几何模型
§5.4 “K字形”及其变形
考点归纳
模型分析
相似的基本模型
相似三角形是几何中重要的证明模型之一,是全等三角形的推广,分析图形间的关系离不开数量的计算.相似和勾股是产生等式的主要依据(其他依据还有面积法,三角函数等),因此要掌握相似三角形的基本图形,体会其各种 演变和联系.现将基本模型总结如下:
模型一 A字形; 模型二 X(8)字形; 模型三 K字形(一线三等角)。
对于“A字形”及“ X字形”(或作平行线或其他辅助线去构造“AX字形”)问题,一般利用平行线分线段成比例定理或相似三角形的判定、性质去进行比例变形、等量代换,寻找中间比,从而将问题解决.
考点3-1
典例精讲
K字形(一线三等角)
【例1】如图,△ACB为等腰直角三角形,点O是斜边AB的中点,∠EOF=45 .
⑴求证:△AOE∽△BFO;⑵若AB=4,求AE·BF的值.
A
C
B
O
F
E
3
2
1
⑴证明:∵△ACB为等腰直角三角形
∴△AOE∽△BFO.
∴∠A=∠B=45 ,∠3+∠2=135 .
∵∠EOF=45 .
∴∠1+∠2=135 .
∴∠3=∠1.
⑵解:∵△AOE∽△BFO.
∴AE BF=4
∴AE:BO=AO:BF.
∴AE BF=AO BO.
∵AO=BO=2.
∴△ABP∽△PCD.
【变式】如图,在△ABC中,AB=AC,点D、P分别在边AC、BC上,且∠APD=∠B.
求证:AC·CD=CP·BP.
证明:∵AB=AC,
∴∠B=∠C.
∵∠APD=∠B,
∴∠APD=∠C.
∵∠APC=∠B+∠BAP,∠APC=∠APD+∠CPD.
∴∠B+∠BAP=∠APD+∠CPD.
∴∠BAP=∠CPD.
∴
=
BP
CD
BA
CP
∵AB=AC.
∴AC·CD=CP·BP.
C
A
D
B
P
考点3-1
变式训练
K字形(一线三等角)
考点3-1
知识归纳
K字型模型分析
K字型(一线三等角)模型分析 类别 正K型(一线三等角) 正K型变形 斜K型
图形
条件
结论
∠B=∠1=∠D
△ABC∽△CDE
A
E
F
C
B
D
1
A(F)
E
C
B
D
1
A
E
C
B
D
1
F
B
C
D
E
A
1
∠B=∠1=∠C
△FBD∽△DCE
B
D
E
C
A
1
2
∠1=∠2=∠ACE
△ABC∽△CDE
【例2】如图,在正方形ABCD中,E是边AB上的一动点(不与点A、B重合),连接DE,点A关于直线DE的对称点为F,连接EF并延长交BC于点G,连接DG,过点E作EH⊥DE交DG的延长线于点H,连接BH.
(1)求证:GF=GC;(2)用等式表示线段BH与AE的数量关系,并证明.
D
H
B
E
C
A
F
G
解:(1)连接DF,
Q
∴△DEH是等腰直角三角形.
过点H作HQ⊥AB交AB延长线于点Q.
(2)BH= AE.
2
易证∠EDG= ∠ADC=45 .
1
2
易证△DAE≌△EQH.
∴AE=QH,DA=EQ.
∵AB=DA=EQ.
∴AE=BQ.
∴BQ=HQ.
∴△BQH是等腰直角三角形.
∴BH= HQ= AE.
2
2
易证△DGF≌△DGC,
易证△DAE≌△DFE,
∴GF=GC.
考点3-2
典例精讲
K字形(一线三直角)
Q
【变形一】由(1),(3)→(2)如图,E是正方形ABCD的边AB上一点,∠CBH=45 ,过点E作EH⊥DE交BH于点H,求证:∠EDH=45 .
(1)∠DEH=90 ;(2)∠EDH=45 ;(3)∠CBH=45 .
D
H
B
E
C
A
G
【分析】可以采用构造三垂直思路,但是对于△DAE和△EQH,并没有已知的相等线段,此路不通.
不同的条件下方法可能会不同,利用好题目的已知条件,比如此处∠CBH=45 如何运用
证明:在AD边上取点F使得AF=AE,连接EF.
∴∠DFE=135 =∠EBH,易证∠FDE=∠BEH,DF=EB,
∴△DFE≌△EBH,
∴DE=DH.
∴△DEH是等腰直角三角形,
∴∠DEH=45 .
考点3-2
变式训练
K字形(一线三直角)
(1)∠DEH=90 ;(2)∠EDH=45 ;(3)∠CBH=45 .
【变形二】由(2),(3)→(1)如图,E是正方形ABCD的边AB上一点,
∠EDH=∠CBH=45 ,求证:DE⊥EH.
∴∠DEH=∠DBH=90 .
D
H
B
E
C
A
G
O
证明:∵∠EDH=45 ,∠EBH=90 +45 =135 .
∴∠EDH+∠EBH=180 .
∴B、E、D、H四点共圆,连接BD.
∴DE⊥EH.
考点3-2
变式训练
K字形(一线三直角)
考点3-2
知识归纳
K字形(一线三直角)
一线三直角模型分析 类别 同侧 异侧 拓展(图形背景)
图形
条件 结论 ∠D=∠ACB=∠E=90
△ADC∽△CEB
A
O
E
C
B
D
y
O
x
C
D
A
B
A
F
C
D
B
E
G
C
A
B
D
E
∠B=∠ACE=∠CDE=90
△ABC∽△CDE
y
O
x
B
A
考点3-3
典例精讲
构造一线三直角
【例3】如图,已知抛物线y=-0.5x2与直线AB交于A(-2,-4),B两点连接AO,BO,若∠AOB=90 ,则点B的坐标为________.
C
D
(1,- )
1
2
y
O
x
B
A
C
D
如图,在平面直角坐标系中,等腰直角三角形OAB的一个顶点在原点处,∠ABO=90 ,OB=AB,已知点A(2,4),则点B的坐标为______.
y
x
B
A
O
(3,1)
E
F
N
M
考点3-3
变式训练
构造一线三直角
考点3-3
知识归纳
构造一线三直角
构造一线三直角模型分析 类别 一线两直角 一线一直角 一直角 图形
条件 结论 F
∠AEC=∠ACB=90
C
B
A
E
E
F
A
B
C
B
C
A
E
F
C
A
B
E
F
A
C
B
E
F
△AEC∽△CFB
∠ACB=90
△AEC∽△CFB
∠ACB=90
△AEC∽△CFB
知识梳理
课堂小结
K字形及其变形
模型说明
识别
方法
构造一线三直角的基本步骤
一线三等角
一线三直角是一个常见的相似模型,指的是有三个直角的顶点在同一条直线上构成的相似图形,也有称三垂直模型、K型图或M型图.
(一线三等角不仅可以是直角,也可以是锐角或钝角)
(1)找图中已知的直角,顺着这个直角的顶点寻找或者构造模型中的一线;
(2)构造其他直角,构造的直角的顶点必须在同一条直线上,这条直线可能在已知角的外部,也可能穿过这个角.
若出现一直角的顶点在一条直线上的形式,就可以构造两侧的直角三角形,利用全等三角形或相似三角形解决相关问题.本质就是找角、定线、构相似.
1.如图四边形ABCD、EFGH是正方形,NHMC是矩形,A,B,N,E,F五点在同一直线上,若正方形ABCD,EFGH的边长分别为3,4,BN=2,则NH为_____.
2.如图,四边形ACDF是正方形,∠CEA和∠ABF都是直角且点E,A,B三点共线,AB=4,则阴影部分的面积是____.
A
M
H
G
F
E
N
B
C
D
2 13
提升能力
强化训练
K字形及其变形
8
B
A
F
D
C
E
M
N
y
x
O
B
A
提升能力
强化训练
K字形及其变形
3.如图,点A是反比例函数y=-的图像上的一个动点,连接OA,若将线段0A绕点0顺时针旋转90 得到线段0B,则点B所在的反比例函数表达式为_____.
4.如图,在平面直角坐标系中,A(2,0),B(0,1),AC由AB绕点A顺时针旋转90 而得,则AC所在直线的解析式是_______.
5.如图,已知A(0,3),B(4,0),点C在第一象限,且AC=5,BC=10,则直线OC的函数表达式为_______.
2
x
y=
y=2x-4
D
y
O
x
C
B
A
H
y
x
O
C
A
B
y= x
4
5
提升能力
强化训练
K字形及其变形
6.如图,已知△ABC中∠ABC=90 ,AB=BC,△ABC三个顶点在相互平行的三条直线上,且l1与l2之间的距离为2,l2与l3之间的距离为3,则AC的长是_____.
7.如图,在平面直角坐标系中,矩形OABC的两边OA,OC分别在x轴,y轴上,且OA=8,OC=4.若把矩形OABC绕着点O逆时针旋转,使点A恰好落在BC边上的点A1处,则点B的对应点B1的坐标为______________.
E
D
l1
l3
l2
A
C
B
H
N
M
2 17
E
F
B
y
x
A
O
C
A1
C1
B1
H
M
( , )
4 3-2
2 3+4
提升能力
强化训练
K字形及其变形
8.如图,点A(0,8),点B(4,0),连接AB,点M、N分别是OA,AB的中点,在射线MN上有一动点P.若△ABP是直角三角形,则点P的坐标是__________________.
9.如图,在平面直角坐标系中,点C(0,4),射线CE∥x轴,直线y=-0.5x+b交线段OC于点B,交x轴于于点A,D是射线CE上一点,若存在点D,使得△ABD恰为等腰直角三角形,则b的值为___________.
y
x
A
M
B
O
N
P
P
H
P
H
(12,4)或( ,4)
2 5+2
y
O
x
C
E
A
B
D
y
O
x
C
E
A
B
D
y
O
x
C
E
A
B
D
H
H
4
3
8
3
或
或2
提升能力
强化训练
K字形及其变形
A
F
E
C
D
B
10.如图,正方形ABCD的边长为16,在BC边上取一动点E,连接AE,作EF⊥AE,交CD边于点F.若CF=3,求CE的长.
解:∵四边形ABCD为正方形.
∴∠B=∠C=90 .
∴∠BAE=∠AEB=90 .
∵EF⊥AE.
∴∠AEF=90 .
∴∠AEB+∠CEF=90 .
∴∠BAE=∠CEF.
∴△ABE∽△ECF.
∴
CE
BA
=
CF
BE
即:
CE
16
=
3
16-CE
∴CE=4或12.
提升能力
强化训练
K字形及其变形
11.如图,△ABC≌△DEF(点A,B分别与点D,E对应),AB=AC=5,BC=6,△ABC固定不动,△DEF运动,并满足点E在BC边从B向C移动(点E不与B,C重合),DE始终经过点A,EF与AC边交于点M,当△AEM是等腰三角形时,求BE的长.
A
M
C
E
B
F
D
解:∵∠AEF=∠B=∠C,且∠AME>∠C.
∴AE≠AM.
①当AE=EM时,则△ABE≌△ECM.
∴CE=AB=5.
∴BE=BC-CE=6-5=1.
②当AM=EM时,则∠MAE=∠MEA,
∴∠MAE+∠BAE=∠MEA+∠CEM.
∴∠MAB=∠CEA.
∵∠C=∠C,
∴△ABC∽△ECA
∴CE:AC=AC:CB
∴BE=BC-CE=
11
6
∴CE=
25
6
提升能力
强化训练
K字形及其变形
12.如图,在△ABC中,AB=AC,∠BAC=90 ,点D是边BC的中点,点E在边AB上(点E不与点A,B重合),点F在边AC上,连接DE,DF,∠EDF=45 .
求证:.
B
A
C
D
F
E
证明:∵∠BDF=∠BDE+∠EDF,∠BDE=∠C+∠CFD.
∴∠BDE+∠EDF=∠C+∠CFD.
∵∠C=∠EDF=45 .
∴∠BDE=∠CFD.
∴△BDE∽△CFD.
∴
BE
CD
=
BD
CF
=
DE
DF
∴
BE
CD
·
BD
CF
=( )2
DE
DF
∵BD=CD.
∴
BE
CF
DE2
DF2
=
13.如图,在菱形ABCD中,∠ABC=120 ,将菱形沿EF折叠,使点A恰好落在对角线BD上的点G处(不与B、D重合),若DG=2,BG=6,则BE的长为____.
A
G
D
C
F
E
B
易证△FGD∽△GEB
【分析】等边翻折得到一线三等角.
由题意可得:∠FDG=∠FGE=∠GBE=60 .
FG
GE
=
DG
EB
=
FD
GB
∴
设FG=x,则AE=x,DF=8-x,设GE=y,则AE=y,BE=8-y.
代入得:
x
y
=
2
8-y
=
8-x
6
解得:y=
26
5
∴BE=8- =
26
5
14
5
14
5
提升能力
强化训练
K字形及其变形
提升能力
强化训练
K字形及其变形
14.如图,在平面直线坐标系中,点M(2,1)是直线AB:y=x上一点,将直线AB绕点M顺时针旋转45 得到直线CD,求CD解析式.
y=- x+
5
3
1
3
y
O
x
B
A
C
M
D
45
E
P
F
P
E
F
y
O
x
B
A
C
M
D
45
提升能力
强化训练
K字形及其变形
【变式】如图,在平面直线坐标系中,点M(2,1)是直线AB:y=x上一点,将直线AB绕点M顺时针旋转α得到直线CD,且tanα=,求直线CD解析式.
y
O
x
B
A
C
M
D
α
E
P
F
y=- x+
15
7
4
7
提升能力
强化训练
K字型(一线三直角)
1.如图,∠BAD=∠ACB=90 ,AB=AD,AC=4BC,若CD=5,则S四边形ABCD=_____.
2.如图,已知∠ACB=90 ,AD=BC,CD=BE,AE与BD相交于点F,则∠AFD=____.
3.如图,在四边形ABCD中,AD=3,CD=4,∠ABC=∠ACB=∠ADC=45 ,则BD=____
A
D
C
B
10
E
A
F
E
D
C
B
G
G
45
F
E
A
O
B
C
D
34
提升能力
强化训练
K字型(一线三直角)
4.如图,在平面直角坐标系中,点A(0,2),点B(4,0),点C在第一象限内,若△ABC为等边三角形,则点C的坐标为________.
5.抛物线y=x2-4x+3与坐标轴交于A,B,C三点,点P在抛物线上,PE⊥BC于点E,若PE=2CE,则点P的坐标为_________.
y
x
C
B
A
O
F
E
D
2
3
y
O
x
B
A
C
E
P
M
N
3
3
m
m
2m
2m
(3m,3+m)
(5,3 3 )
( , )
13
3
40
9
21
3
2 3
3
7
提升能力
强化训练
K字型(一线三直角)
6.如图直角梯形ABCD中,AD//BC,AB⊥BC,AD=2,BC=3,将腰CD以D为中心逆时针旋转90°至ED,连AE、CE,则△ADE的面积是____.
1
N
M
A
E
D
C
B
提升能力
强化训练
K字型(一线三直角)
D
B
C
A
F
E
7.如图,正方形ABCD和Rt△AEF,AB=5,AE=AF=4,连接BF,DE.若△AEF绕点A旋转,当∠ABF最大时,S△ADE=___.
【分析】动态问题先分析何时∠ABF最大.F点轨迹是以点A为圆心,AF为半径的圆,当BF与圆相切时,∠ABF最大,分别过点E、F作直线DA的垂线,垂足分别记为M、N,
M
N
D
B
C
A
F
E
M
N
易证△AME≌△FNA,
∴EM=AN=4×3/5=12/5.
∴S△ADE=1/2×5×12/5=6.
6
提升能力
强化训练
K字型(一线三直角)
8.如图,在△ABC中,AB=AC=5,BC=4,D为边AB上一动点(B点除外),以CD为一边作正方形CDEF,连接BE,则△BDE面积的最大值为___.
【分析】求三角形的面积,可以首先考虑面积公式,以BD为底,需作高 分别过C、E作BA的垂线,垂足分别记为点M、N.
F
A
D
E
B
C
N
M
8
故△BDE面积的最大值为8.
易证△DMC≌△END,
由tan∠ABC=1/2得:CM=4,BM=8,
设BD=x,则EN=DM=8-x.
∴S△BDE=1/2x(8-x)=-1/2x2+4x.
当x=4时,S△BDE取到最大值8.
提升能力
强化训练
K字型(一线三直角)
9.如图,正方形ABCD的对角线AC上有一点E,且CE=4AE,点F在DC的延长线上,连接EF,过点E作EG⊥EF,交CB的延长线于点G,连接FG并延长,交4C的延长线于点P,若AB=5,CF=2,则线段EP的长是______.
N
M
P
B
F
C
G
A
D
E
P
B
F
C
G
A
D
E
H
【分析】有直角便可考虑构造三垂直.如下左图,过点E作EM⊥CD交CD于M点,过点G作GN⊥ME交ME延长线于点N,易证△FME≌△ENG,连接GA,点F作FH⊥AP交AP于H点,
易证△GAE∽△EHF,
∴△PHF∽△PAG.
∴FH:GA=PH:PA.
解得:PH=
3 2
2
∴PE=
13 2
2
提升能力
强化训练
K字型(一线三直角)
10.如图,点P为矩形ABCD的对角线BD上一点,PE⊥AP交BC于点E,若AD=10,
DC=6,求的值.
M
N
A
P
E
C
D
B
提升能力
强化训练
K字型(一线三直角)
11.如图,在四边形ABCD中,∠ABC=90 ,AB=3,BC=4,DA=5,求BD的长
H
A
D
C
B
提升能力
强化训练
K字型(一线三直角)
12.在△ABC中,∠ABC=90 ,tan∠BAC=.
(1)如图①,分别过A、C两点作经过点B的直线的垂线,垂足分别为点M、N.若点B恰好是线段MN的中点,求tan∠BAM的值;
(2)如图②,P是边BC的延长线上一点,∠APB=∠BAC,求tan∠PAC的值.
B
A
C
M
N
图①
D
E
A
C
P
B
图②
提升能力
强化训练
K字型(一线三直角)
13.两块三角板如图放置,已知∠BAC=∠ADC=90 ,∠ABC=45 ,∠ACD=30 ,
BC=cm.
(1)分别求线段AD,CD的长度;
(2)求BD2的值。
E
A
C
D
B
提升能力
强化训练
K字型(一线三直角)
14.如图,已知直线:y=-x+6分别与x轴、y轴交于点B,A,以AB为斜边向△OAB外作等腰直角△ABC,AC=BC.
(1)分别写出点A、B的坐标;
(2)求线段OC的长度。
y
O
x
B
A
C
F
E
(1)A(0,6),B(10,0)
(2)
M
N
8 2
同课章节目录
