专题6.1直角三角---直角三角形的应用模型-中考数学二轮复习必会几何模型剖析(全国通用)
文档属性
| 名称 | 专题6.1直角三角---直角三角形的应用模型-中考数学二轮复习必会几何模型剖析(全国通用) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-26 00:00:00 | ||
图片预览





文档简介
(共12张PPT)
专题六 直角三角形模型
人教版中考第二轮总复习---几何模型
§6.1 常见的直角三角形模型
考点归纳
知识梳理
解直角三角形的实际应用模型
解直角三角形是中考的重要内容之一,直角三角形边、角关系的知识是解直角三角形的基础.将实际问题转化为数学问题是关键,通常是通过作高线或垂线转化为解直角三角形问题,在解直角三角形时要注意三角函数的选取,避免计算复杂.在解题中,若求解的边,角不在直角三角形中,应先添加辅助线,构造直角三角形.为了提高解题能力,快速提分本专题把常用的模型及演变题型总结如下:
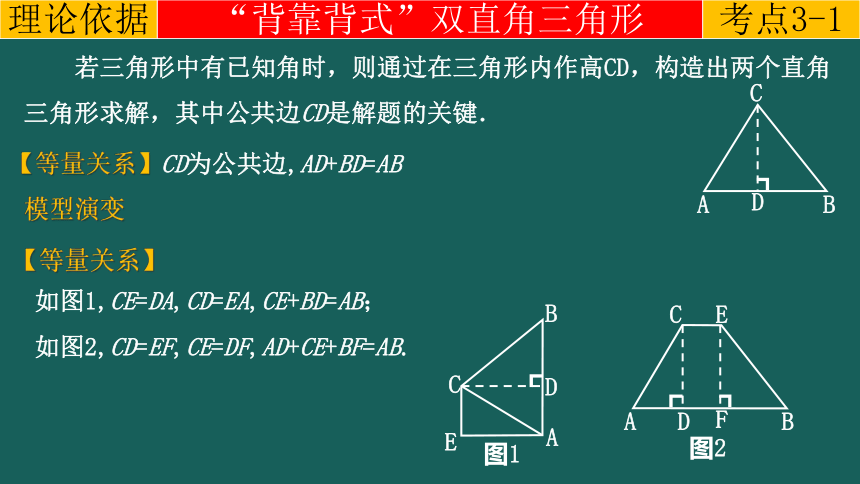
若三角形中有已知角时,则通过在三角形内作高CD,构造出两个直角三角形求解,其中公共边CD是解题的关键.
考点3-1
理论依据
“背靠背式”双直角三角形
【等量关系】CD为公共边,AD+BD=AB
A
C
D
B
模型演变
A
图1
B
D
C
E
A
F
D
E
C
B
图2
【等量关系】
如图2,CD=EF,CE=DF,AD+CE+BF=AB.
如图1,CE=DA,CD=EA,CE+BD=AB;
【例1】如图,一艘轮船位于灯塔P的北偏东60 方向且与灯塔P的距离为80海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东45 方向上的B处,求此时轮船所在的B处与灯塔P的距离(结果保留根号).
考点3-1
典例精讲
“背靠背式”双直角三角形
解:作PC⊥AB于C点.
∴∠APC=30 ,∠BPC=45 ,AP=80(海里).
在Rt△APC中,cos∠APC=
PC
PA
∴PC=PA cos∠APC=
40 3(海里)
在Rt△PCB中,cos∠BPC=
PC
PB
答:此时轮船所在的B处与灯塔P的距离是40 6海里.
∴PB= = =40 6(海里).
PC
cos∠BPC
40 3
cos45
P
60
C
B
A
45
北
考点3-1
针对训练
“背靠背式”双直角三角形
1.为加快城乡对接,对A,B两地间的公路进行改建.如图A,B两地之间有一座山,汽车原来从A地到B地需途经C地沿折线ACB行驶,开通隧道后,可沿直线AB行驶.已知BC=80km,∠A=45 ,∠B=30 .开通隧道后,汽车从A地到B地大约可以少走多少千米 (结果精确到0.1km,参考数据:≈1.41,≈1.732)
A
C
B
D
答:开通隧道后,汽车从A地到B地大约可以少走27.2千米.
解:如图,过点C作CD⊥AB于点D.
在Rt△BCD中.
∵BC=80,∠B=30 .
∴DC=BC·sin30 =40,BD=BC·cos30 =40 3
在Rt△ACD中.
∵∠A=45 .
∴AD=CD=40,AC=40 2
∴AC+BC=40 2+80≈40×1.41+80=136.4
∴AB=AD+BD=40+40 3≈40+40×1.73=109.2
∴AC+BC-AB=136.4-109.2=27.2
考点3-2
理论依据
“叠合式”双直角三角形
若三角形中有已知角,通过在三角形外作高BC,构造有公共直角的两个三角形求解,其中公共边BC是解题的关键.
【等量关系】
如图1,AD+DC=AC;
如图2,DC-BC=DB.
A
B
D
C
图1
图2
A
D
B
C
模型演变1
如图4,AF=CE,AC=FE,BC+AF=BE.
【等量关系】
如图3,DF=EC,DE=FC,BF+DE=BC,AE+DF=AC;
A
E
F
C
B
D
图3
A
F
图4
D
B
C
E
考点3-2
理论依据
“叠合式”双直角三角形
模型演变3
如图9,BC=FG,BF=CG,
EF+BC=EG,BD+DF=BF,AC+BD+DF=AG.
【等量关系】
如图8,BC=FG,BF=CG,
AC+BF=AG,EF+BC=EG;
A
图8
B
C
F
G
E
C
A
B
D
F
G
E
图9
模型演变2
【等量关系】
如图5,BE+EC=BC;
如图6,EC-BC=BE;
如图7,AC=FG,AF=CG,AD+DC=FG,BC+AF=BG.
A
E
D
C
B
图5
C
D
A
E
B
图6
F
图7
D
A
B
C
G
【例1-1】如图,某高速公路建设中需要确定隧道AB的长度.已知在离地面1500m,高度C处的飞机,测量人员测得正前方A、B两点处的俯角分别为60 和45 ,求隧道AB的长.
考点3-2
典例精讲
“叠合式”双直角三角形
解:由题意得∠ACO=30 ,∠CBO=45 ,
在Rt△COA中,
在Rt△COB中,OB=OC=1500m,
A
D
C
B
O
∵tan30 =
OA
OC
∴OA=CO×tan30 =1500× =500 m,
3
3
3
∴AB=(1500-500 )m
3
答:隧道AB的长约为(1500-500 )m.
3
1.一幢楼的楼顶端挂着一幅长10米的宣传条幅AB,某数学兴趣小组在一次活动中,测量该楼的高度,但被建筑物FGHM挡住,不能直接到达楼的底部,他们在点D处测得条幅顶端A的仰角∠CDA=45 ,向后退8米到E点,测得条幅底端B的仰角∠CEB=30 (点C,D,E在同一直线上).根据以上数据,帮助该兴趣小组计算楼高AC.(精确到0.01米,参考数据:≈1.732,≈1.414)
考点3-2
针对训练
“叠合式”双直角三角形
A
H
G
C
B
E
D
M
F
解:设AC=x米,则BC=(x-10)米.
在Rt△ACD中,∠CDA=∠CAD=45 .
∴CD=AC=x.
在Rt△ECB中,CE=CD+DE=x+8.
答:楼高AC约为34.59米.
∴tan∠CEB= ,
BC
CE
解 得,x= ≈34.59.
8+10 3
3-1
x-10
x+8
=tan30 =
3
3
即:
2.为积极宣传国家相关政策,某村在一山坡的顶端的平地上竖立一块宣传牌AB.小明为测得宣传牌的高度,他站在山脚C处测得宣传牌的顶端A的仰角为40 ,已知山坡CD的坡度i=1:2,山坡CD的长度为4米,山坡顶端D与宣传牌底端B的水平距离为2米,求宣传牌的高度AB.(精确到0.1米,参考数据:sin40 ≈0.64,cos40 ≈0.77,tan40 ≈0.84,≈2.24)
考点3-2
针对训练
“叠合式”双直角三角形
A
C
D
B
E
F
∴设DF=x米,则CF=2x米.
解:延长AB 交CE于点E,过点D作DF⊥CE于点F.
∴BD=EF,BE=DF.
在Rt△CDF中
∵山坡CD的坡度i=1:2.
由勾股定理,得x2+(2x)2=(4 5)2.
解得x=4.
∴CE=CF+EF=8+2=10米.
在Rt△ACE中.
AE
CE
∵tan40 =
∴AE≈10×0.84=8.4(米).
∴AB=AE-BE≈8.4-4=4.4(米).
答:宣传牌的高度AB为4.4米.
∴四边形BDFE是矩形.
∴DF=4米,CF=8米.
分别解两个直角三角形,其中公共边BC是解题的关键.
考点3-3
理论依据
“拥抱型”双直角三角形
【等量关系】
A
D
C
B
模型演变
A
D
E
C
F
B
图1
A
D
E
C
B
图2
A
B
C
E
D
图3
G
如图1,BF+FC+CE=BE;
如图2,BC+CE=BE;
如图3,AB=GE,AG=BE,BC+CE=AG,DG+AB=DE.
4.如图,两幢建筑物AB和CD,AB⊥BD,CD⊥BD,AB=15m,CD=20m.AB和CD之间有一景观池,小双在A点测得池中喷泉处E点的俯角为42 ,在C点测得E点的俯角为45 ,点B、E、D在同一直线上.求两幢建筑物之间的距离BD.(结果精确到0.1m,参考数据:sin42 ≈0.67,cos42 ≈0.74,tan42 ≈0.90)
解:由题意得:∠AEB=42 ,∠DEC=45 .
∵AB⊥BD,DC⊥BD.
∴在Rt△ABE中,∠ABE=90 .
∴BE= ≈15÷0.90=
50
3
15
tan42
∵AB=15,∠AEB=42 ,tan∠AEB=
AB
BE
在Rt△DEC中,∠CDE=90
∠DEC=∠DCE=45 ,CD=20.
∴ED=CD=20
∴BD=BE+ED≈ +20≈36.7 m
50
3
答:两幢建筑物之间的距离BD约为36.7 m.
考点3-3
典例精讲
“拥抱型”双直角三角形
A
E
D
C
B
42
45
专题六 直角三角形模型
人教版中考第二轮总复习---几何模型
§6.1 常见的直角三角形模型
考点归纳
知识梳理
解直角三角形的实际应用模型
解直角三角形是中考的重要内容之一,直角三角形边、角关系的知识是解直角三角形的基础.将实际问题转化为数学问题是关键,通常是通过作高线或垂线转化为解直角三角形问题,在解直角三角形时要注意三角函数的选取,避免计算复杂.在解题中,若求解的边,角不在直角三角形中,应先添加辅助线,构造直角三角形.为了提高解题能力,快速提分本专题把常用的模型及演变题型总结如下:
若三角形中有已知角时,则通过在三角形内作高CD,构造出两个直角三角形求解,其中公共边CD是解题的关键.
考点3-1
理论依据
“背靠背式”双直角三角形
【等量关系】CD为公共边,AD+BD=AB
A
C
D
B
模型演变
A
图1
B
D
C
E
A
F
D
E
C
B
图2
【等量关系】
如图2,CD=EF,CE=DF,AD+CE+BF=AB.
如图1,CE=DA,CD=EA,CE+BD=AB;
【例1】如图,一艘轮船位于灯塔P的北偏东60 方向且与灯塔P的距离为80海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东45 方向上的B处,求此时轮船所在的B处与灯塔P的距离(结果保留根号).
考点3-1
典例精讲
“背靠背式”双直角三角形
解:作PC⊥AB于C点.
∴∠APC=30 ,∠BPC=45 ,AP=80(海里).
在Rt△APC中,cos∠APC=
PC
PA
∴PC=PA cos∠APC=
40 3(海里)
在Rt△PCB中,cos∠BPC=
PC
PB
答:此时轮船所在的B处与灯塔P的距离是40 6海里.
∴PB= = =40 6(海里).
PC
cos∠BPC
40 3
cos45
P
60
C
B
A
45
北
考点3-1
针对训练
“背靠背式”双直角三角形
1.为加快城乡对接,对A,B两地间的公路进行改建.如图A,B两地之间有一座山,汽车原来从A地到B地需途经C地沿折线ACB行驶,开通隧道后,可沿直线AB行驶.已知BC=80km,∠A=45 ,∠B=30 .开通隧道后,汽车从A地到B地大约可以少走多少千米 (结果精确到0.1km,参考数据:≈1.41,≈1.732)
A
C
B
D
答:开通隧道后,汽车从A地到B地大约可以少走27.2千米.
解:如图,过点C作CD⊥AB于点D.
在Rt△BCD中.
∵BC=80,∠B=30 .
∴DC=BC·sin30 =40,BD=BC·cos30 =40 3
在Rt△ACD中.
∵∠A=45 .
∴AD=CD=40,AC=40 2
∴AC+BC=40 2+80≈40×1.41+80=136.4
∴AB=AD+BD=40+40 3≈40+40×1.73=109.2
∴AC+BC-AB=136.4-109.2=27.2
考点3-2
理论依据
“叠合式”双直角三角形
若三角形中有已知角,通过在三角形外作高BC,构造有公共直角的两个三角形求解,其中公共边BC是解题的关键.
【等量关系】
如图1,AD+DC=AC;
如图2,DC-BC=DB.
A
B
D
C
图1
图2
A
D
B
C
模型演变1
如图4,AF=CE,AC=FE,BC+AF=BE.
【等量关系】
如图3,DF=EC,DE=FC,BF+DE=BC,AE+DF=AC;
A
E
F
C
B
D
图3
A
F
图4
D
B
C
E
考点3-2
理论依据
“叠合式”双直角三角形
模型演变3
如图9,BC=FG,BF=CG,
EF+BC=EG,BD+DF=BF,AC+BD+DF=AG.
【等量关系】
如图8,BC=FG,BF=CG,
AC+BF=AG,EF+BC=EG;
A
图8
B
C
F
G
E
C
A
B
D
F
G
E
图9
模型演变2
【等量关系】
如图5,BE+EC=BC;
如图6,EC-BC=BE;
如图7,AC=FG,AF=CG,AD+DC=FG,BC+AF=BG.
A
E
D
C
B
图5
C
D
A
E
B
图6
F
图7
D
A
B
C
G
【例1-1】如图,某高速公路建设中需要确定隧道AB的长度.已知在离地面1500m,高度C处的飞机,测量人员测得正前方A、B两点处的俯角分别为60 和45 ,求隧道AB的长.
考点3-2
典例精讲
“叠合式”双直角三角形
解:由题意得∠ACO=30 ,∠CBO=45 ,
在Rt△COA中,
在Rt△COB中,OB=OC=1500m,
A
D
C
B
O
∵tan30 =
OA
OC
∴OA=CO×tan30 =1500× =500 m,
3
3
3
∴AB=(1500-500 )m
3
答:隧道AB的长约为(1500-500 )m.
3
1.一幢楼的楼顶端挂着一幅长10米的宣传条幅AB,某数学兴趣小组在一次活动中,测量该楼的高度,但被建筑物FGHM挡住,不能直接到达楼的底部,他们在点D处测得条幅顶端A的仰角∠CDA=45 ,向后退8米到E点,测得条幅底端B的仰角∠CEB=30 (点C,D,E在同一直线上).根据以上数据,帮助该兴趣小组计算楼高AC.(精确到0.01米,参考数据:≈1.732,≈1.414)
考点3-2
针对训练
“叠合式”双直角三角形
A
H
G
C
B
E
D
M
F
解:设AC=x米,则BC=(x-10)米.
在Rt△ACD中,∠CDA=∠CAD=45 .
∴CD=AC=x.
在Rt△ECB中,CE=CD+DE=x+8.
答:楼高AC约为34.59米.
∴tan∠CEB= ,
BC
CE
解 得,x= ≈34.59.
8+10 3
3-1
x-10
x+8
=tan30 =
3
3
即:
2.为积极宣传国家相关政策,某村在一山坡的顶端的平地上竖立一块宣传牌AB.小明为测得宣传牌的高度,他站在山脚C处测得宣传牌的顶端A的仰角为40 ,已知山坡CD的坡度i=1:2,山坡CD的长度为4米,山坡顶端D与宣传牌底端B的水平距离为2米,求宣传牌的高度AB.(精确到0.1米,参考数据:sin40 ≈0.64,cos40 ≈0.77,tan40 ≈0.84,≈2.24)
考点3-2
针对训练
“叠合式”双直角三角形
A
C
D
B
E
F
∴设DF=x米,则CF=2x米.
解:延长AB 交CE于点E,过点D作DF⊥CE于点F.
∴BD=EF,BE=DF.
在Rt△CDF中
∵山坡CD的坡度i=1:2.
由勾股定理,得x2+(2x)2=(4 5)2.
解得x=4.
∴CE=CF+EF=8+2=10米.
在Rt△ACE中.
AE
CE
∵tan40 =
∴AE≈10×0.84=8.4(米).
∴AB=AE-BE≈8.4-4=4.4(米).
答:宣传牌的高度AB为4.4米.
∴四边形BDFE是矩形.
∴DF=4米,CF=8米.
分别解两个直角三角形,其中公共边BC是解题的关键.
考点3-3
理论依据
“拥抱型”双直角三角形
【等量关系】
A
D
C
B
模型演变
A
D
E
C
F
B
图1
A
D
E
C
B
图2
A
B
C
E
D
图3
G
如图1,BF+FC+CE=BE;
如图2,BC+CE=BE;
如图3,AB=GE,AG=BE,BC+CE=AG,DG+AB=DE.
4.如图,两幢建筑物AB和CD,AB⊥BD,CD⊥BD,AB=15m,CD=20m.AB和CD之间有一景观池,小双在A点测得池中喷泉处E点的俯角为42 ,在C点测得E点的俯角为45 ,点B、E、D在同一直线上.求两幢建筑物之间的距离BD.(结果精确到0.1m,参考数据:sin42 ≈0.67,cos42 ≈0.74,tan42 ≈0.90)
解:由题意得:∠AEB=42 ,∠DEC=45 .
∵AB⊥BD,DC⊥BD.
∴在Rt△ABE中,∠ABE=90 .
∴BE= ≈15÷0.90=
50
3
15
tan42
∵AB=15,∠AEB=42 ,tan∠AEB=
AB
BE
在Rt△DEC中,∠CDE=90
∠DEC=∠DCE=45 ,CD=20.
∴ED=CD=20
∴BD=BE+ED≈ +20≈36.7 m
50
3
答:两幢建筑物之间的距离BD约为36.7 m.
考点3-3
典例精讲
“拥抱型”双直角三角形
A
E
D
C
B
42
45
同课章节目录
