专题7.2选择压轴题---操作题解题技巧-中考数学二轮复习必会几何模型剖析(全国通用)
文档属性
| 名称 | 专题7.2选择压轴题---操作题解题技巧-中考数学二轮复习必会几何模型剖析(全国通用) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-26 00:00:00 | ||
图片预览




文档简介
(共22张PPT)
专题七 客观题的解题技巧
人教版中考第二轮总复习---几何模型
§7.2 操作题解题技巧
考点归纳
知识梳理
操作题---选择压轴题
近几年各省的中考选择压轴题,多次考查了操作题,操作题常常是在基本图形的基础上进行变形得到的,在解决这一类问题的时候,常常需要通过几何变换进行转化,逐渐转化为“基本图形”,再运用“基本图形”的知识解决.
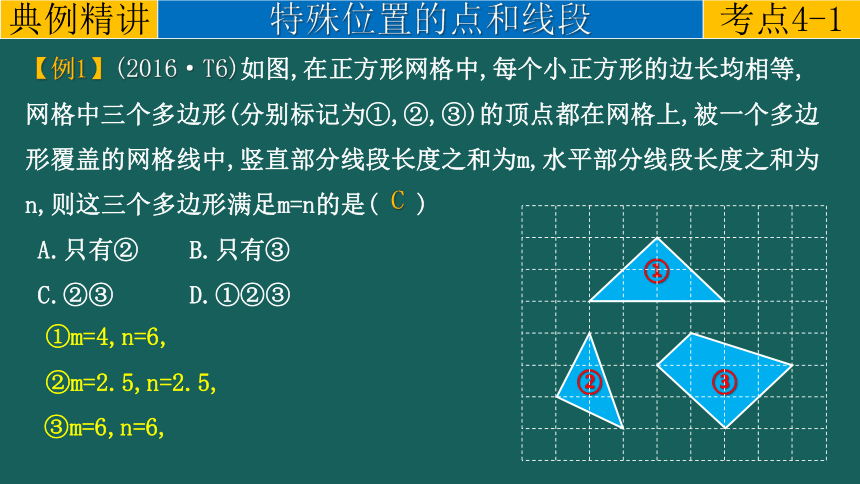
【例1】(2016·T6)如图,在正方形网格中,每个小正方形的边长均相等,网格中三个多边形(分别标记为①,②,③)的顶点都在网格上,被一个多边形覆盖的网格线中,竖直部分线段长度之和为m,水平部分线段长度之和为n,则这三个多边形满足m=n的是( )
A.只有② B.只有③
C.②③ D.①②③
C
③
①
②
考点4-1
典例精讲
特殊位置的点和线段
①m=4,n=6,
②m=2.5,n=2.5,
③m=6,n=6,
1.蜂巢的构造非常美丽,科学,如图是由7个形状,大小完全相同的正六边形组成的网络,正六边形的顶点称为格点,△ABC的顶点都在格点上,设定AB边如图所示,则△ABC是直角三角形的个数有( )个
A.4 B.6 C.8 D.10
①以AB是直角边,
D
A
B
②以AB是斜边,
符合要求的点C有4个.
以点A为直顶点,
符合要求的点C有3个;
以点B为直顶点,
符合要求的点C有3个;
∴符合要求的点C共有10个;
考点4-1
针对训练
特殊位置的点和线段
A
D
C
B
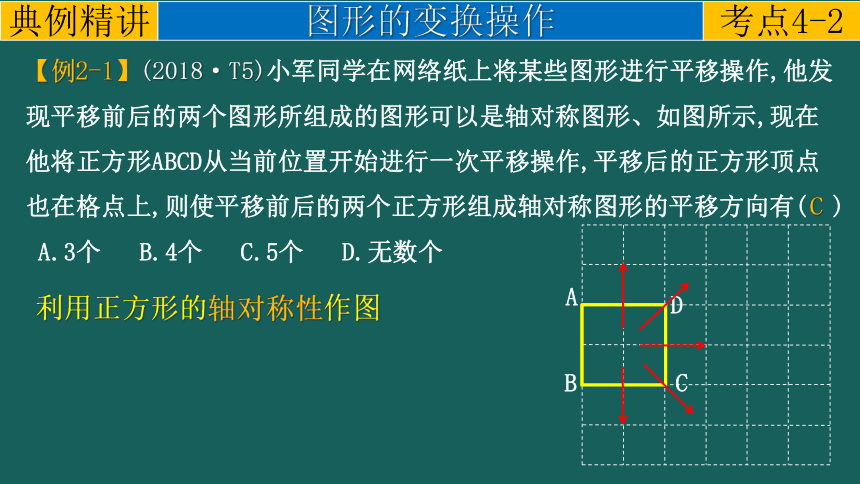
【例2-1】(2018·T5)小军同学在网络纸上将某些图形进行平移操作,他发现平移前后的两个图形所组成的图形可以是轴对称图形、如图所示,现在他将正方形ABCD从当前位置开始进行一次平移操作,平移后的正方形顶点也在格点上,则使平移前后的两个正方形组成轴对称图形的平移方向有( )
A.3个 B.4个 C.5个 D.无数个
C
考点4-2
典例精讲
图形的变换操作
利用正方形的轴对称性作图
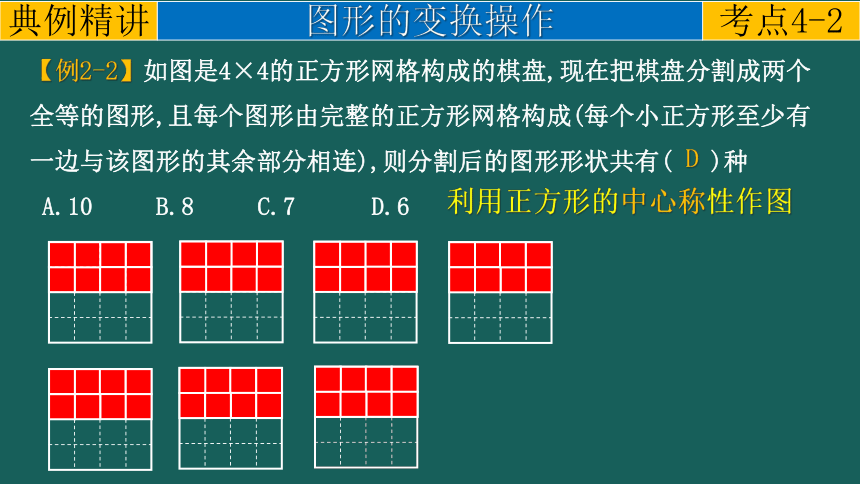
【例2-2】如图是4×4的正方形网格构成的棋盘,现在把棋盘分割成两个全等的图形,且每个图形由完整的正方形网格构成(每个小正方形至少有一边与该图形的其余部分相连),则分割后的图形形状共有( )种
A.10 B.8 C.7 D.6
考点4-2
典例精讲
图形的变换操作
利用正方形的中心称性作图
D
【例3】(2019·T6)如图,由10根完全相同的小棒拼接而成,请你再添2根与前面完全相同的小棒,拼接后的图形恰好有3个菱形的方法共有( )
A.3种 B.4种 C.5种 D.6种
D
考点4-3
典例精讲
构造特殊图形
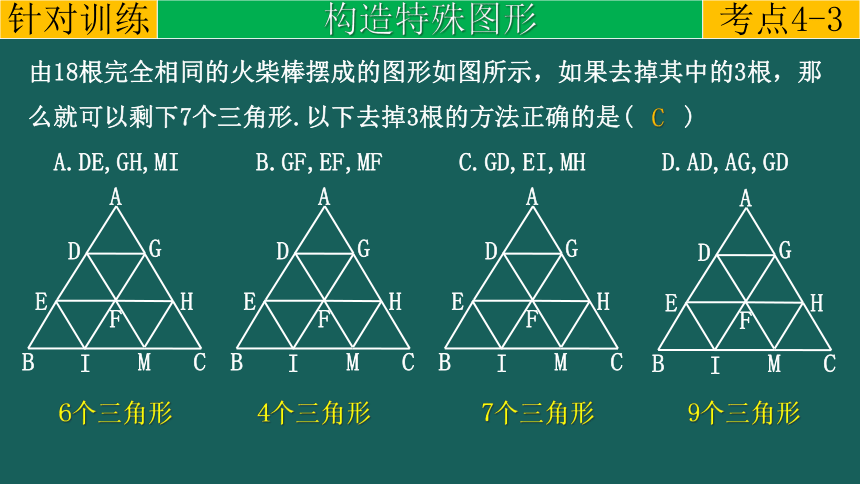
由18根完全相同的火柴棒摆成的图形如图所示,如果去掉其中的3根,那么就可以剩下7个三角形.以下去掉3根的方法正确的是( )
A.DE,GH,MI B.GF,EF,MF C.GD,EI,MH D.AD,AG,GD
C
考点4-3
针对训练
构造特殊图形
A
H
F
E
G
D
B
I
M
C
A
H
F
E
G
D
B
I
M
C
A
H
F
E
G
D
B
I
M
C
A
H
F
E
G
D
B
I
M
C
6个三角形
4个三角形
7个三角形
9个三角形
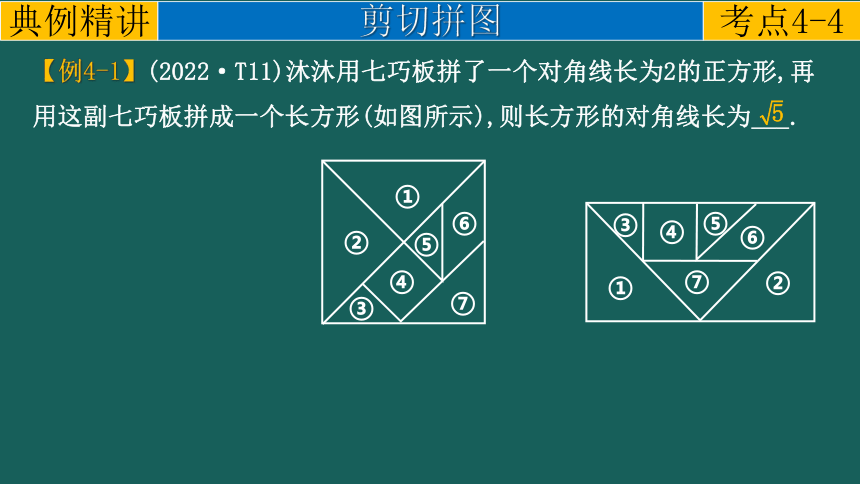
【例4-1】(2022·T11)沐沐用七巧板拼了一个对角线长为2的正方形,再用这副七巧板拼成一个长方形(如图所示),则长方形的对角线长为___.
考点4-4
典例精讲
剪切拼图
5
①
⑤
⑥
④
⑦
③
②
①
⑤
⑥
④
⑦
③
②
【例4-2】(2021·T6)如图是用七巧板拼接成的一个轴对称图形(忽略拼接线),小亮改变①的位置,将①分别摆放在图中左,下,右的位置(摆放时无缝隙不重叠),还能拼接成不同轴对称图形的个数为( )
A.2 B.3 C.4 D.5
B
考点4-4
典例精讲
剪切拼图
左
下
右
1
1
1
上
1
①
2
2
1.观察下列方格中阴影部分所示的图形(每一小方格的边长为1),如果将它们沿方格边线或对角线剪开重新拼接,不能拼成正方形的是( )
D
A
B
D
C
正方形的边长为
2 2
正方形的边长为
正方形的边长为
正方形的边长为
2
10
11
考点4-4
针对训练
剪切拼图
2.由沈康身教授所著,数学家吴文俊作序的《数学的魅力》一书中记载了这样一个故事:如图,三姐妹为了平分一块边长为1的祖传正方形地毯,先将地毯分割成七块,再拼成三个小正方形(阴影部分).则图中AB=_______.
①
②
③
④
⑤
⑥
⑦
①
②
③
④
⑤
⑥
A
B
考点4-4
针对训练
剪切拼图
C
D
F
E
2-1
1.如图所示是6×6的正方形网格,每个小正方形的顶点称为格点,已知点A和点B在格点上,在网格中的格点上另找一点C,使A,B,C三点构成一个三点构成一个直角三角形,则这样的点C共有( )
A.7个 B.8个 C.9个 D.10个
C
A
B
提升能力
强化训练
操作问题
2.在如图所示网格中,已知线段AB,现要在网格内再确定格点C和格点D.某数学小组在探究时发现以下结论,其中不正确的是( )
A.将线段AB平移得到线段CD,使四边形ABDC为正方形的有2种;
B.将线段AB平移得到线段CD,使四边形ABDC为菱形(正方形除外)的有3种;
C.将线段AB平移得到线段CD,使四边形ABDC为矩形(正方形除外)的有2种;
D.不存在以AB为对角线的四边形ACBD是菱形.
C
提升能力
强化训练
操作问题
A
B
C
D
C
D
3.如图是由三个相同的小正方形组成的图形,在图中补画一个相同的小正方形,使补画后四个小正方形所组成图形为轴对称图形的方法有( )种
A.1 B.2 C.3 D.4
D
提升能力
强化训练
操作问题
利用正方形的轴对称性作图
4.如图,在3×3的正方形网格中,△ABC的顶点都在小正方形的顶点出,这样的三角形称为“格点三角形”,在此网格中与△ABC成轴对称的格点三角形一共有( )个
A.6 B.7 C.8 D.9
A
C
B
A
C
B
A
C
B
A
C
B
C
提升能力
强化训练
操作问题
利用正方形的轴对称性作图
5.如图是由三个全等的菱形拼接而成的图形,若平移其中一个菱形,与其它两个菱形重新拼接(无覆盖,有公共的顶点),并使拼接成的图形为轴对称的图形,则平移的方式共有( )种
A.5 B.6 C.7 D.8
D
提升能力
强化训练
操作问题
利用菱形的轴对称性作图
6.如图是由7个全等的菱形(有一个内角为60 )组成的网格,菱形的顶点成为格点,顺次连接图中的4个格点,能练出矩形的方法共有( )
A.6 种 B.8 种 C.10 种 D.12 种
3种
+3种
+2种
+2种
=10种
C
提升能力
强化训练
操作问题
提升能力
强化训练
操作问题
7.如图,某小区有东西方向的街道3条,南北方向的街道4条,从位置A出发沿街道行进到达位置B,要求路程最短,研究共有多少种不同的走法,小东是这样想的:要使路程最短,就不能走“回头路”,只能分五步来完成,其中三步向右行进,两步向上行进,如果用数字“1”表示向右行进,数字“2”表示向上行进,那么“11221”与“11212”就表示两种符
合要求的不同走法,那么符合要求的不同走法共有____种.
10
A
B
1
1
2
1
2
2
2
1
2
1
2
1
2
1
2
2
1
1
1
2
1
2
1
2
1
2
2
1
1
1
1
1
1
y
O
x
4
3
2
1
1
2
-1
-2
8.二次函数y=-(x-2)2+的图像与x轴围成的封闭区域内(包括边界),横纵坐标都是整数的点有___个
7
提升能力
强化训练
操作问题
(2, )
9
4
(1, )
5
4
(3, )
5
4
9.在平面直角坐标系中,把横、纵坐标都是整数的点叫做整点,如图,已知反比例函数y=(k>0,x>0与二次函数y=-+4的图象所围成的阴影部分中(不含边界)有5个整点,则k的值可能为( ) A.4 B.3 C.2 D.1
4
C
(1,3)
(1,2)
(1,1)
(2,3)
(2,2)
(2,1)
(3,2)
(3,1)
2≤x<3
×
×
×
提升能力
强化训练
操作问题
y
O
x
C
y
O
x
A
B
P
10.如图,在平面直角坐标系中,正方形OABC的边长为4,边OA,OC分别在x轴,y轴的正半轴上,把正方形OABC的内部及边上横纵坐标均为整数的点称为好点,已知点P为抛物线y=-(x-m)2+m+2的顶点,若点P在正方形OABC的内部,该抛物线下方(包括边界)恰好存在8个好点,则m的取值范围为_____________.
提升能力
强化训练
操作问题
5-
2
13
≤m<1
专题七 客观题的解题技巧
人教版中考第二轮总复习---几何模型
§7.2 操作题解题技巧
考点归纳
知识梳理
操作题---选择压轴题
近几年各省的中考选择压轴题,多次考查了操作题,操作题常常是在基本图形的基础上进行变形得到的,在解决这一类问题的时候,常常需要通过几何变换进行转化,逐渐转化为“基本图形”,再运用“基本图形”的知识解决.
【例1】(2016·T6)如图,在正方形网格中,每个小正方形的边长均相等,网格中三个多边形(分别标记为①,②,③)的顶点都在网格上,被一个多边形覆盖的网格线中,竖直部分线段长度之和为m,水平部分线段长度之和为n,则这三个多边形满足m=n的是( )
A.只有② B.只有③
C.②③ D.①②③
C
③
①
②
考点4-1
典例精讲
特殊位置的点和线段
①m=4,n=6,
②m=2.5,n=2.5,
③m=6,n=6,
1.蜂巢的构造非常美丽,科学,如图是由7个形状,大小完全相同的正六边形组成的网络,正六边形的顶点称为格点,△ABC的顶点都在格点上,设定AB边如图所示,则△ABC是直角三角形的个数有( )个
A.4 B.6 C.8 D.10
①以AB是直角边,
D
A
B
②以AB是斜边,
符合要求的点C有4个.
以点A为直顶点,
符合要求的点C有3个;
以点B为直顶点,
符合要求的点C有3个;
∴符合要求的点C共有10个;
考点4-1
针对训练
特殊位置的点和线段
A
D
C
B
【例2-1】(2018·T5)小军同学在网络纸上将某些图形进行平移操作,他发现平移前后的两个图形所组成的图形可以是轴对称图形、如图所示,现在他将正方形ABCD从当前位置开始进行一次平移操作,平移后的正方形顶点也在格点上,则使平移前后的两个正方形组成轴对称图形的平移方向有( )
A.3个 B.4个 C.5个 D.无数个
C
考点4-2
典例精讲
图形的变换操作
利用正方形的轴对称性作图
【例2-2】如图是4×4的正方形网格构成的棋盘,现在把棋盘分割成两个全等的图形,且每个图形由完整的正方形网格构成(每个小正方形至少有一边与该图形的其余部分相连),则分割后的图形形状共有( )种
A.10 B.8 C.7 D.6
考点4-2
典例精讲
图形的变换操作
利用正方形的中心称性作图
D
【例3】(2019·T6)如图,由10根完全相同的小棒拼接而成,请你再添2根与前面完全相同的小棒,拼接后的图形恰好有3个菱形的方法共有( )
A.3种 B.4种 C.5种 D.6种
D
考点4-3
典例精讲
构造特殊图形
由18根完全相同的火柴棒摆成的图形如图所示,如果去掉其中的3根,那么就可以剩下7个三角形.以下去掉3根的方法正确的是( )
A.DE,GH,MI B.GF,EF,MF C.GD,EI,MH D.AD,AG,GD
C
考点4-3
针对训练
构造特殊图形
A
H
F
E
G
D
B
I
M
C
A
H
F
E
G
D
B
I
M
C
A
H
F
E
G
D
B
I
M
C
A
H
F
E
G
D
B
I
M
C
6个三角形
4个三角形
7个三角形
9个三角形
【例4-1】(2022·T11)沐沐用七巧板拼了一个对角线长为2的正方形,再用这副七巧板拼成一个长方形(如图所示),则长方形的对角线长为___.
考点4-4
典例精讲
剪切拼图
5
①
⑤
⑥
④
⑦
③
②
①
⑤
⑥
④
⑦
③
②
【例4-2】(2021·T6)如图是用七巧板拼接成的一个轴对称图形(忽略拼接线),小亮改变①的位置,将①分别摆放在图中左,下,右的位置(摆放时无缝隙不重叠),还能拼接成不同轴对称图形的个数为( )
A.2 B.3 C.4 D.5
B
考点4-4
典例精讲
剪切拼图
左
下
右
1
1
1
上
1
①
2
2
1.观察下列方格中阴影部分所示的图形(每一小方格的边长为1),如果将它们沿方格边线或对角线剪开重新拼接,不能拼成正方形的是( )
D
A
B
D
C
正方形的边长为
2 2
正方形的边长为
正方形的边长为
正方形的边长为
2
10
11
考点4-4
针对训练
剪切拼图
2.由沈康身教授所著,数学家吴文俊作序的《数学的魅力》一书中记载了这样一个故事:如图,三姐妹为了平分一块边长为1的祖传正方形地毯,先将地毯分割成七块,再拼成三个小正方形(阴影部分).则图中AB=_______.
①
②
③
④
⑤
⑥
⑦
①
②
③
④
⑤
⑥
A
B
考点4-4
针对训练
剪切拼图
C
D
F
E
2-1
1.如图所示是6×6的正方形网格,每个小正方形的顶点称为格点,已知点A和点B在格点上,在网格中的格点上另找一点C,使A,B,C三点构成一个三点构成一个直角三角形,则这样的点C共有( )
A.7个 B.8个 C.9个 D.10个
C
A
B
提升能力
强化训练
操作问题
2.在如图所示网格中,已知线段AB,现要在网格内再确定格点C和格点D.某数学小组在探究时发现以下结论,其中不正确的是( )
A.将线段AB平移得到线段CD,使四边形ABDC为正方形的有2种;
B.将线段AB平移得到线段CD,使四边形ABDC为菱形(正方形除外)的有3种;
C.将线段AB平移得到线段CD,使四边形ABDC为矩形(正方形除外)的有2种;
D.不存在以AB为对角线的四边形ACBD是菱形.
C
提升能力
强化训练
操作问题
A
B
C
D
C
D
3.如图是由三个相同的小正方形组成的图形,在图中补画一个相同的小正方形,使补画后四个小正方形所组成图形为轴对称图形的方法有( )种
A.1 B.2 C.3 D.4
D
提升能力
强化训练
操作问题
利用正方形的轴对称性作图
4.如图,在3×3的正方形网格中,△ABC的顶点都在小正方形的顶点出,这样的三角形称为“格点三角形”,在此网格中与△ABC成轴对称的格点三角形一共有( )个
A.6 B.7 C.8 D.9
A
C
B
A
C
B
A
C
B
A
C
B
C
提升能力
强化训练
操作问题
利用正方形的轴对称性作图
5.如图是由三个全等的菱形拼接而成的图形,若平移其中一个菱形,与其它两个菱形重新拼接(无覆盖,有公共的顶点),并使拼接成的图形为轴对称的图形,则平移的方式共有( )种
A.5 B.6 C.7 D.8
D
提升能力
强化训练
操作问题
利用菱形的轴对称性作图
6.如图是由7个全等的菱形(有一个内角为60 )组成的网格,菱形的顶点成为格点,顺次连接图中的4个格点,能练出矩形的方法共有( )
A.6 种 B.8 种 C.10 种 D.12 种
3种
+3种
+2种
+2种
=10种
C
提升能力
强化训练
操作问题
提升能力
强化训练
操作问题
7.如图,某小区有东西方向的街道3条,南北方向的街道4条,从位置A出发沿街道行进到达位置B,要求路程最短,研究共有多少种不同的走法,小东是这样想的:要使路程最短,就不能走“回头路”,只能分五步来完成,其中三步向右行进,两步向上行进,如果用数字“1”表示向右行进,数字“2”表示向上行进,那么“11221”与“11212”就表示两种符
合要求的不同走法,那么符合要求的不同走法共有____种.
10
A
B
1
1
2
1
2
2
2
1
2
1
2
1
2
1
2
2
1
1
1
2
1
2
1
2
1
2
2
1
1
1
1
1
1
y
O
x
4
3
2
1
1
2
-1
-2
8.二次函数y=-(x-2)2+的图像与x轴围成的封闭区域内(包括边界),横纵坐标都是整数的点有___个
7
提升能力
强化训练
操作问题
(2, )
9
4
(1, )
5
4
(3, )
5
4
9.在平面直角坐标系中,把横、纵坐标都是整数的点叫做整点,如图,已知反比例函数y=(k>0,x>0与二次函数y=-+4的图象所围成的阴影部分中(不含边界)有5个整点,则k的值可能为( ) A.4 B.3 C.2 D.1
4
C
(1,3)
(1,2)
(1,1)
(2,3)
(2,2)
(2,1)
(3,2)
(3,1)
2≤x<3
×
×
×
提升能力
强化训练
操作问题
y
O
x
C
y
O
x
A
B
P
10.如图,在平面直角坐标系中,正方形OABC的边长为4,边OA,OC分别在x轴,y轴的正半轴上,把正方形OABC的内部及边上横纵坐标均为整数的点称为好点,已知点P为抛物线y=-(x-m)2+m+2的顶点,若点P在正方形OABC的内部,该抛物线下方(包括边界)恰好存在8个好点,则m的取值范围为_____________.
提升能力
强化训练
操作问题
5-
2
13
≤m<1
同课章节目录
