专题7.3(2)填空多解题---图形的变换-中考数学二轮复习必会几何模型剖析(全国通用)
文档属性
| 名称 | 专题7.3(2)填空多解题---图形的变换-中考数学二轮复习必会几何模型剖析(全国通用) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-26 08:56:23 | ||
图片预览






文档简介
(共20张PPT)
专题七 客观题的解题技巧
人教版中考第二轮总复习---几何模型
§7.3(2) 填空多解题
---图形变换的分类讨论
A
C
B
A
C
B
A
C
B
【例1】如图,已知△ABC中,AB=AC=5,BC=8,将△ABC沿射线BC的方向平移m个单位得到△DEF,顶点A,B,C分别与点D,E,F对应.若以A,D,E为顶点的三角形是等腰三角形,则m的值是_________.
E
D
①AE=AD=BE
H
cosB=
考点3-1
典例精讲
平移中的分类讨论
BH
BE
4
5
=
F
E
F
D
②AD=DE=5
(E)
F
D
③AE=DE
或5
或8
25
8
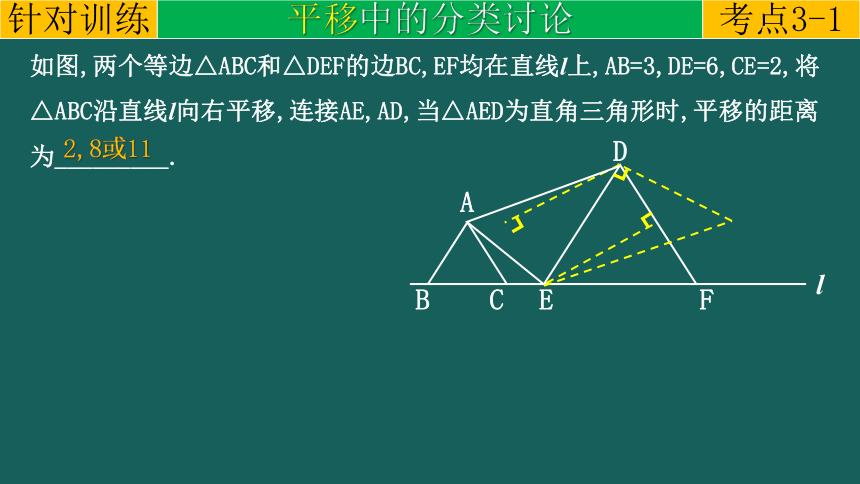
如图,两个等边△ABC和△DEF的边BC,EF均在直线l上,AB=3,DE=6,CE=2,将△ABC沿直线l向右平移,连接AE,AD,当△AED为直角三角形时,平移的距离为_________.
F
E
D
A
C
B
l
2,8或11
考点3-1
针对训练
平移中的分类讨论
【例2】(2012·T14)如图正方形ABCD与正三角形AEF的顶点A重合,将△AEF绕其顶点A旋转,在旋转过程中,当BE=DF时,∠BAE的大小可以是__________.
15 或165
E
F
C
D
B
A
E
F
考点3-2
典例精讲
旋转中的分类讨论
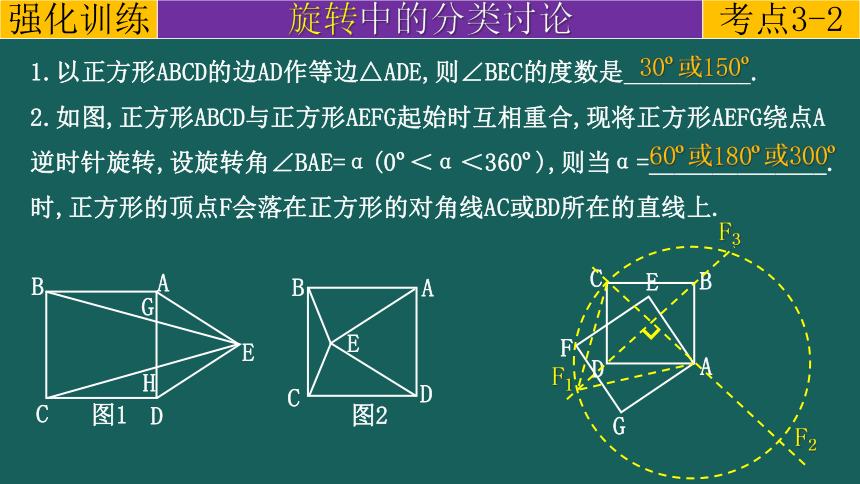
1.以正方形ABCD的边AD作等边△ADE,则∠BEC的度数是__________.
2.如图,正方形ABCD与正方形AEFG起始时互相重合,现将正方形AEFG绕点A逆时针旋转,设旋转角∠BAE=α(0 <α<360 ),则当α=______________.时,正方形的顶点F会落在正方形的对角线AC或BD所在的直线上.
A
H
G
E
D
C
B
图1
A
E
D
C
B
图2
30 或150
考点3-2
强化训练
旋转中的分类讨论
60 或180 或300
A
D
F
E
C
B
G
F1
F2
F3
【例3-1】(2017·T12)已知点A(0,4),B(7,0),C(7,4),连接AC,BC得到矩形AOBC,点D的边AC上,将边OA沿OD折叠,点A的对应边为A .若点A 到矩形较长两对边的距离之比为1:3,则点A 的坐标为_______________________.
A
B
C
x
O
y
D
A
A
A
考点3-2
典例精讲
翻折中的分类讨论
( 7,3)
或( 15-1)
或(2 3,-2)
【例3-2】(2020·T12)矩形纸片ABCD,AD=8cm,AB=4cm,折叠纸片,使折痕经过点B,交AD边于点E,点A落在点A 处,展平后得到折痕BE,同时得到线段BA ,
EA ,不再添加其它线段,当图中存在30 角时,AE=___________________cm.
A
E
A
C
D
B
(1)当∠ABE=30 时.AE=
(2)当∠ABA =30 时.AE=
(3)当∠AEB=30 时.AE=
考点3-3
典例精讲
翻折中的分类讨论
4 3
3
或4 3
或(8-4 3)
4 3
3
4 3
(8-4 3)
A
C
D
B
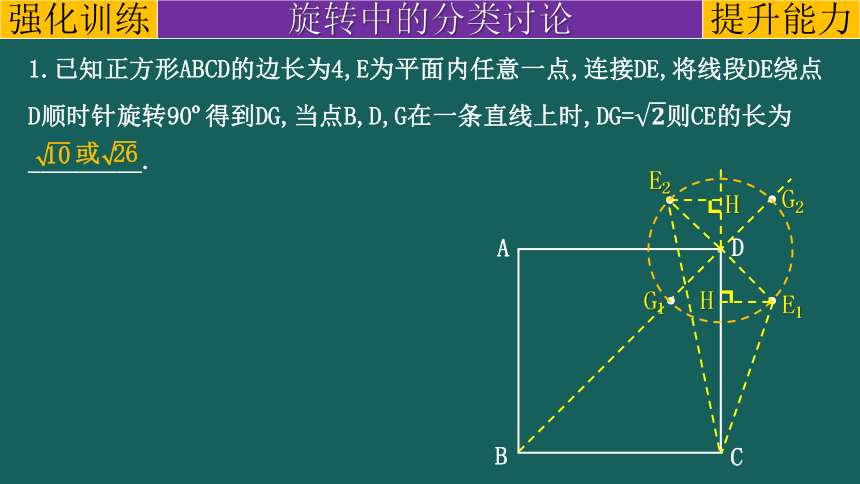
1.已知正方形ABCD的边长为4,E为平面内任意一点,连接DE,将线段DE绕点D顺时针旋转90 得到DG,当点B,D,G在一条直线上时,DG=则CE的长为_________.
G1
E2
G2
E1
提升能力
强化训练
旋转中的分类讨论
H
H
10
或 26
2.如图,在Rt△ABC中,∠B=90 ,BC=2AB=8,点D,E分别是边BC,AC的中点,连接DE.将△EDC绕点C按顺时针方向旋转一周,当△EDC旋转至A,D,E三点在同一直线上时,线段BD的长为__________.
A
C
D
E
B
D
E
D
E
提升能力
强化训练
旋转中的分类讨论
4 5
12 5
5
或
3.如图,在△ABC中,∠ACB=90 ,AC=BC=5,在AC、BC边上分别截取CD=CE=3,连接DE.将△DCE绕着点C顺时针旋转θ角(0 <θ<360 ),连接BE、AD.四边形CDFE是正方形时,则AF=______.
提升能力
强化训练
旋转中的分类讨论
A
E
B
D
C
A
E
B
D
C
F
A
E
B
D
C
F
7或1
4.如图,正方形ABCD的边长为4,在AD边上存在一个动点E(不和点A,D重合),沿BE把△ABE折叠,当点A的对应点A 恰好落在正方形ABCD的对称轴上时,AE的长为____________________.
A
E
C
D
B
A
A
C
D
B
E
A
M
N
A
C
D
B
E
A
M
N
知识点二
强化训练
翻折中的分类讨论
8-4 3
或4 2-4
4 3
3
或
5.如图,在矩形ABCD中,AB=6,AD=10,点E是AD的中点,点P是线段AB上一动点,连接PE,将△AEP沿PE折叠,使点A落在点A 处,连接A D、A C,当△A DC为等腰三角形时,则AP的长为_______.
A
E
C
D
B
P
A
N
M
H
5
3
5
4
x
x
3-x
1
A M2+PM2=A P2
12+(3-x)2=x2
x=5/3
A
E
C
D
B
P
A
6
6
5
5
x
x
6-x
PB2+BC2=PC2
(6-x)2+102=(6+x)2
x=25/6
提升能力
强化训练
翻折中的分类讨论
A
E
C
D
B
A
6
6
10
8
P
(不合题意,舍去)
5
3
25
6
或
tan∠AEP= =
4
3
AP
5
AP= >6
20
3
1.如图,在矩形ABCD中,AD=6,AB=8,点E是CD边上一个动点,将△ADE沿AE折叠,当点D的对应点D 落在矩形ABCD的对称轴上时,DE=___________.
A
D
D
E
C
B
6
6
3
3
x
A
D
D
E
C
B
6
x
4-x
x
6
4
x
知识点二
强化训练
翻折中的分类讨论
【变式】如图,在矩形ABCD中,AD=5,AB=7,点E是CD上的一个动点,将△ADE沿AE折叠,当点D的对应点D 落在∠ABC的平分线上时,DE=______.
M
N
x
A
D
D
E
C
B
5
x
7-x
5
x2+(7-x)2=52
x1=3,x2=4
y
2
4-y
y
1
22+(4-y)2=y2
y=5/2
M
A
D
D
E
C
B
5
N
x
x
7-x
5
y
y
3-y
12+(3-y)2=y2
y=5/3
或9-3 5
2 3
5
2
或
5
3
3 3
3 3-x
2 5
6-2 5
(3 3-x)2+32=x2
x=2 3
(6-2 5)2+(4-x)2=x2
x=9-3 5
10.如图,已知矩形ABCD中,AB=6,AD=8,点G为AD的中点,点H沿D→C→B的路径运动,连接GH,沿GH对折,使点D落在点D 处.当点D 到矩形边(DA除外)的距离为2时,∠DGH的度数为______________.
30 ,45 或60
A
G
C
D
B
D
H
H
D
A
G
C
D
B
D
H
A
G
C
D
B
D
(H)
提升能力
强化训练
翻折中的分类讨论
6.如图,在矩形ABCD中,AB=6,BC=12,点E是射线BC上一动点,将△ABE沿AE翻折得到△AEF,延长AF交CD的延长线于点G,当BE=3EC时,线段DG=______.
6
6
9
3
x
9-x
9-x
x2+62=(9-x)2
x=2.5
E
G
F
A
D
C
B
H
E
G
F
A
D
C
B
H
FH:GD=AF:AD
2.5:GD=6:12
GD=5
6
6
12
6
x
18-x
18-x
x2+62=(18-x)2
x=8
FH:GD=AF:AD
8:GD=6:12
GD=16
5或16
提升能力
强化训练
翻折中的分类讨论
E
F
7.如图,在矩形ABCD中,点G在AD上,且GD=AB=1,AG=2,点E是线段BC上的一个动点(点E不与点B、C重合),连接GB,GE,将△GBE关于直线GE对称的三角形记作△GFE,当点E运动到使点F落在矩形任意一边所在的直线上时,则所有满足条件的线段BE的长是___________.
A
G
C
D
B
F1
E1
A
G
C
D
B
F2
H
提升能力
强化训练
翻折中的分类讨论
E2
A
G
C
D
B
F3
E3
H
5
3
或2
或 5
8.如图,在△ABC中,∠BAC=90 ,AB=AC=6点M为线段AB上一点,且BM=2,点N为BC边上一动点,连接MN,将△BMN沿MN折叠,点B的对应点为点P,当PN与△ABC的一边平行时,则CN的长为_____________________.
N
A
M
C
B
P
A
M
C
B
P
N
A
M
C
B
P
N
知识点二
强化训练
翻折中的分类讨论
6 2-2
或4 2+2
或4 2-2
9.如图,在Rt△ABC纸片中,∠C=90 ,AC=6,BC=8,点D在边BC上,以AD为折痕,将△ABD折叠得到△AB D,AB 与边BC交于点E.若△DEB 为直角三角形,则BD的长是______.
2或5
A
B
C
B
E
D
B
E
D
F
提示:∠ADC=∠ADF
BD=2
A
B
C
B
(E)
D
BD=5
知识点二
强化训练
翻折中的分类讨论
11.△ABC中,AB=AC,∠A=36 ,D为AC边上一点,将△CBD沿直线BD翻折,使翻折后的点C的对应点C 恰好落在△ABC的边上,则∠CBD=__________.
D
A
C
B
C
36 或18
D
C
A
C
B
∠CBD=18
∠CBD=36
提升能力
强化训练
翻折中的分类讨论
12.如图,在Rt△ABC中,∠C=90 ,∠B=30 ,点D为CB的中点,且CB=12,点E为AB上一点,把△BDE沿DE翻折得到△FDE,若FE与△ABC的某边垂直,则BE的长为____________________________.
FE⊥AB,BE=
B
H
提升能力
强化训练
翻折中的分类讨论
B
D
A
C
F
E
B
D
A
C
F
E
H
FE⊥BC,BE=
B
D
A
C
F
E
FE⊥AC,BE=6,
B
D
A
C
E
F
FE⊥BC,BE=
B
D
A
C
E
F
FE⊥BC,BE=
或3 3-3
或3 3+3
6
或2 3
或6 3
3 3-3
2 3
3 3+3
6 3
专题七 客观题的解题技巧
人教版中考第二轮总复习---几何模型
§7.3(2) 填空多解题
---图形变换的分类讨论
A
C
B
A
C
B
A
C
B
【例1】如图,已知△ABC中,AB=AC=5,BC=8,将△ABC沿射线BC的方向平移m个单位得到△DEF,顶点A,B,C分别与点D,E,F对应.若以A,D,E为顶点的三角形是等腰三角形,则m的值是_________.
E
D
①AE=AD=BE
H
cosB=
考点3-1
典例精讲
平移中的分类讨论
BH
BE
4
5
=
F
E
F
D
②AD=DE=5
(E)
F
D
③AE=DE
或5
或8
25
8
如图,两个等边△ABC和△DEF的边BC,EF均在直线l上,AB=3,DE=6,CE=2,将△ABC沿直线l向右平移,连接AE,AD,当△AED为直角三角形时,平移的距离为_________.
F
E
D
A
C
B
l
2,8或11
考点3-1
针对训练
平移中的分类讨论
【例2】(2012·T14)如图正方形ABCD与正三角形AEF的顶点A重合,将△AEF绕其顶点A旋转,在旋转过程中,当BE=DF时,∠BAE的大小可以是__________.
15 或165
E
F
C
D
B
A
E
F
考点3-2
典例精讲
旋转中的分类讨论
1.以正方形ABCD的边AD作等边△ADE,则∠BEC的度数是__________.
2.如图,正方形ABCD与正方形AEFG起始时互相重合,现将正方形AEFG绕点A逆时针旋转,设旋转角∠BAE=α(0 <α<360 ),则当α=______________.时,正方形的顶点F会落在正方形的对角线AC或BD所在的直线上.
A
H
G
E
D
C
B
图1
A
E
D
C
B
图2
30 或150
考点3-2
强化训练
旋转中的分类讨论
60 或180 或300
A
D
F
E
C
B
G
F1
F2
F3
【例3-1】(2017·T12)已知点A(0,4),B(7,0),C(7,4),连接AC,BC得到矩形AOBC,点D的边AC上,将边OA沿OD折叠,点A的对应边为A .若点A 到矩形较长两对边的距离之比为1:3,则点A 的坐标为_______________________.
A
B
C
x
O
y
D
A
A
A
考点3-2
典例精讲
翻折中的分类讨论
( 7,3)
或( 15-1)
或(2 3,-2)
【例3-2】(2020·T12)矩形纸片ABCD,AD=8cm,AB=4cm,折叠纸片,使折痕经过点B,交AD边于点E,点A落在点A 处,展平后得到折痕BE,同时得到线段BA ,
EA ,不再添加其它线段,当图中存在30 角时,AE=___________________cm.
A
E
A
C
D
B
(1)当∠ABE=30 时.AE=
(2)当∠ABA =30 时.AE=
(3)当∠AEB=30 时.AE=
考点3-3
典例精讲
翻折中的分类讨论
4 3
3
或4 3
或(8-4 3)
4 3
3
4 3
(8-4 3)
A
C
D
B
1.已知正方形ABCD的边长为4,E为平面内任意一点,连接DE,将线段DE绕点D顺时针旋转90 得到DG,当点B,D,G在一条直线上时,DG=则CE的长为_________.
G1
E2
G2
E1
提升能力
强化训练
旋转中的分类讨论
H
H
10
或 26
2.如图,在Rt△ABC中,∠B=90 ,BC=2AB=8,点D,E分别是边BC,AC的中点,连接DE.将△EDC绕点C按顺时针方向旋转一周,当△EDC旋转至A,D,E三点在同一直线上时,线段BD的长为__________.
A
C
D
E
B
D
E
D
E
提升能力
强化训练
旋转中的分类讨论
4 5
12 5
5
或
3.如图,在△ABC中,∠ACB=90 ,AC=BC=5,在AC、BC边上分别截取CD=CE=3,连接DE.将△DCE绕着点C顺时针旋转θ角(0 <θ<360 ),连接BE、AD.四边形CDFE是正方形时,则AF=______.
提升能力
强化训练
旋转中的分类讨论
A
E
B
D
C
A
E
B
D
C
F
A
E
B
D
C
F
7或1
4.如图,正方形ABCD的边长为4,在AD边上存在一个动点E(不和点A,D重合),沿BE把△ABE折叠,当点A的对应点A 恰好落在正方形ABCD的对称轴上时,AE的长为____________________.
A
E
C
D
B
A
A
C
D
B
E
A
M
N
A
C
D
B
E
A
M
N
知识点二
强化训练
翻折中的分类讨论
8-4 3
或4 2-4
4 3
3
或
5.如图,在矩形ABCD中,AB=6,AD=10,点E是AD的中点,点P是线段AB上一动点,连接PE,将△AEP沿PE折叠,使点A落在点A 处,连接A D、A C,当△A DC为等腰三角形时,则AP的长为_______.
A
E
C
D
B
P
A
N
M
H
5
3
5
4
x
x
3-x
1
A M2+PM2=A P2
12+(3-x)2=x2
x=5/3
A
E
C
D
B
P
A
6
6
5
5
x
x
6-x
PB2+BC2=PC2
(6-x)2+102=(6+x)2
x=25/6
提升能力
强化训练
翻折中的分类讨论
A
E
C
D
B
A
6
6
10
8
P
(不合题意,舍去)
5
3
25
6
或
tan∠AEP= =
4
3
AP
5
AP= >6
20
3
1.如图,在矩形ABCD中,AD=6,AB=8,点E是CD边上一个动点,将△ADE沿AE折叠,当点D的对应点D 落在矩形ABCD的对称轴上时,DE=___________.
A
D
D
E
C
B
6
6
3
3
x
A
D
D
E
C
B
6
x
4-x
x
6
4
x
知识点二
强化训练
翻折中的分类讨论
【变式】如图,在矩形ABCD中,AD=5,AB=7,点E是CD上的一个动点,将△ADE沿AE折叠,当点D的对应点D 落在∠ABC的平分线上时,DE=______.
M
N
x
A
D
D
E
C
B
5
x
7-x
5
x2+(7-x)2=52
x1=3,x2=4
y
2
4-y
y
1
22+(4-y)2=y2
y=5/2
M
A
D
D
E
C
B
5
N
x
x
7-x
5
y
y
3-y
12+(3-y)2=y2
y=5/3
或9-3 5
2 3
5
2
或
5
3
3 3
3 3-x
2 5
6-2 5
(3 3-x)2+32=x2
x=2 3
(6-2 5)2+(4-x)2=x2
x=9-3 5
10.如图,已知矩形ABCD中,AB=6,AD=8,点G为AD的中点,点H沿D→C→B的路径运动,连接GH,沿GH对折,使点D落在点D 处.当点D 到矩形边(DA除外)的距离为2时,∠DGH的度数为______________.
30 ,45 或60
A
G
C
D
B
D
H
H
D
A
G
C
D
B
D
H
A
G
C
D
B
D
(H)
提升能力
强化训练
翻折中的分类讨论
6.如图,在矩形ABCD中,AB=6,BC=12,点E是射线BC上一动点,将△ABE沿AE翻折得到△AEF,延长AF交CD的延长线于点G,当BE=3EC时,线段DG=______.
6
6
9
3
x
9-x
9-x
x2+62=(9-x)2
x=2.5
E
G
F
A
D
C
B
H
E
G
F
A
D
C
B
H
FH:GD=AF:AD
2.5:GD=6:12
GD=5
6
6
12
6
x
18-x
18-x
x2+62=(18-x)2
x=8
FH:GD=AF:AD
8:GD=6:12
GD=16
5或16
提升能力
强化训练
翻折中的分类讨论
E
F
7.如图,在矩形ABCD中,点G在AD上,且GD=AB=1,AG=2,点E是线段BC上的一个动点(点E不与点B、C重合),连接GB,GE,将△GBE关于直线GE对称的三角形记作△GFE,当点E运动到使点F落在矩形任意一边所在的直线上时,则所有满足条件的线段BE的长是___________.
A
G
C
D
B
F1
E1
A
G
C
D
B
F2
H
提升能力
强化训练
翻折中的分类讨论
E2
A
G
C
D
B
F3
E3
H
5
3
或2
或 5
8.如图,在△ABC中,∠BAC=90 ,AB=AC=6点M为线段AB上一点,且BM=2,点N为BC边上一动点,连接MN,将△BMN沿MN折叠,点B的对应点为点P,当PN与△ABC的一边平行时,则CN的长为_____________________.
N
A
M
C
B
P
A
M
C
B
P
N
A
M
C
B
P
N
知识点二
强化训练
翻折中的分类讨论
6 2-2
或4 2+2
或4 2-2
9.如图,在Rt△ABC纸片中,∠C=90 ,AC=6,BC=8,点D在边BC上,以AD为折痕,将△ABD折叠得到△AB D,AB 与边BC交于点E.若△DEB 为直角三角形,则BD的长是______.
2或5
A
B
C
B
E
D
B
E
D
F
提示:∠ADC=∠ADF
BD=2
A
B
C
B
(E)
D
BD=5
知识点二
强化训练
翻折中的分类讨论
11.△ABC中,AB=AC,∠A=36 ,D为AC边上一点,将△CBD沿直线BD翻折,使翻折后的点C的对应点C 恰好落在△ABC的边上,则∠CBD=__________.
D
A
C
B
C
36 或18
D
C
A
C
B
∠CBD=18
∠CBD=36
提升能力
强化训练
翻折中的分类讨论
12.如图,在Rt△ABC中,∠C=90 ,∠B=30 ,点D为CB的中点,且CB=12,点E为AB上一点,把△BDE沿DE翻折得到△FDE,若FE与△ABC的某边垂直,则BE的长为____________________________.
FE⊥AB,BE=
B
H
提升能力
强化训练
翻折中的分类讨论
B
D
A
C
F
E
B
D
A
C
F
E
H
FE⊥BC,BE=
B
D
A
C
F
E
FE⊥AC,BE=6,
B
D
A
C
E
F
FE⊥BC,BE=
B
D
A
C
E
F
FE⊥BC,BE=
或3 3-3
或3 3+3
6
或2 3
或6 3
3 3-3
2 3
3 3+3
6 3
同课章节目录
