专题7.3(1)填空多解题---特殊三角形-中考数学二轮复习必会几何模型剖析(全国通用)
文档属性
| 名称 | 专题7.3(1)填空多解题---特殊三角形-中考数学二轮复习必会几何模型剖析(全国通用) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-26 00:00:00 | ||
图片预览




文档简介
(共25张PPT)
专题七 客观题的解题技巧
人教版中考第二轮总复习---几何模型
§7.3(1) 填空多解题
---特殊三角形的分类讨论
考点归纳
知识梳理
题型概述
填空多解题是近几年中考的常题型,这类试题综合性较强,在解答时需要灵活运用分类讨论和数形结合的数学思想方法求解,解题时常因考虑不全或不严谨,导致漏解、错解,所以考生必须熟练掌握这一题型的特征与解法.
分类讨论是重要的数学思想,也是重要的解题策略,很多数学问题很难从整体上去解决,若将其划分为几个局部问题,逐个予以解决.
基本方法:
①确定讨论对象以及所讨论对象的全体范围;
②确定分类标准,合理分类,即标准统一、不重不漏、分类互斥;
③对各个分类逐步进行讨论,分层进行,获取阶段性结果;
④最后进行归纳总结,综合得出结论.
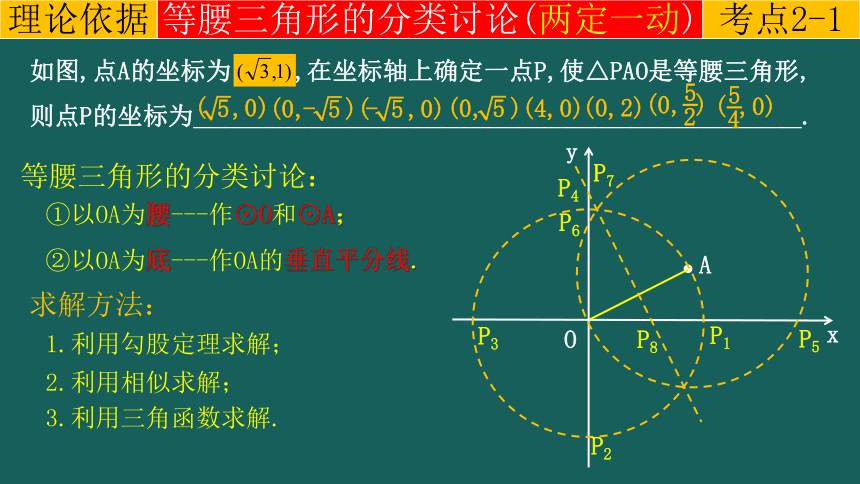
如图,点A的坐标为(2,1),在坐标轴上确定一点P,使△PAO是等腰三角形,则点P的坐标为________________________________________________.
A
O
x
y
P7
P8
P3
P2
P1
P4
P5
P6
考点2-1
理论依据
等腰三角形的分类讨论(两定一动)
(0, )
5
2
( ,0)
5
4
( ,0)
5
(0, )
- 5
( ,0)
- 5
(0, )
5
(4,0)
(0,2)
等腰三角形的分类讨论:
①以OA为腰---作⊙O和⊙A;
②以OA为底---作OA的垂直平分线.
求解方法:
1.利用勾股定理求解;
2.利用相似求解;
3.利用三角函数求解.
【例1-1】(2016·T12)如图,是一张长方形纸片ABCD,已知AB=8,AD=7,E为AB上一点,AE=5,现要剪下一张等腰三角形纸片(AEP),使点P落在长方形ABCD的某一条边上,则等腰三角形AEP的底边长是______________.
P1
P2
P3
D
E
B
A
C
或5 2
或4 5
5
考点2-1
中考真题
等腰三角形的分类讨论(两定一动)
y
O
x
A1
A2
(3,4)
(4,3)
y
O
x
A1
A2
(3,4)
(4,3)
y
O
x
【例1-2】(2022·T12)已知点A在反比例函数y=(x>0)的图象上,点B在x轴正半轴上,若△OAB为等腰三角形,且腰长为5,则AB的长为___________.
考点2-1
中考真题
等腰三角形的分类讨论(一定两动)
以O为圆心,5为半径画⊙O,交⊙O于点A1,A2.
A1
A2
(3,4)
(4,3)
B2
A1B1=A1O=5
B1
B1
AB=
2 5
H
B2
H
AB=
10
5
或2 5
或 10
OA1=OB1=5
OA2=OB2=5
A2B2=A2O=5
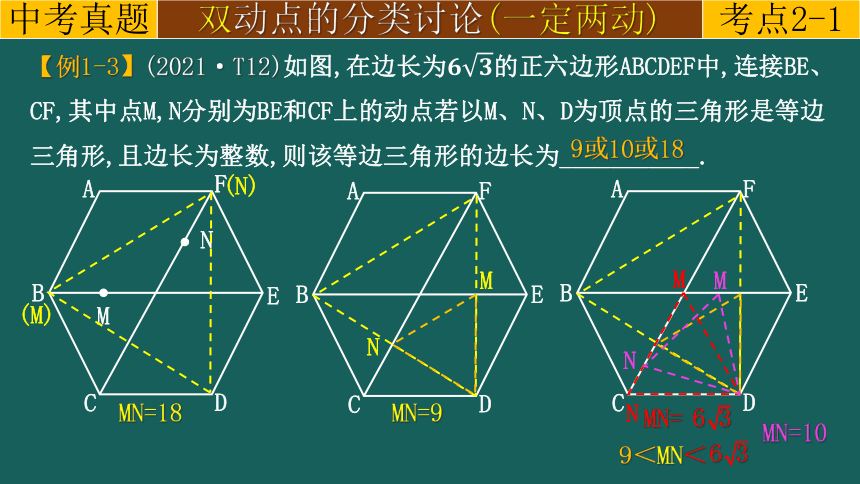
【例1-3】(2021·T12)如图,在边长为的正六边形ABCDEF中,连接BE、CF,其中点M,N分别为BE和CF上的动点若以M、N、D为顶点的三角形是等边三角形,且边长为整数,则该等边三角形的边长为___________.
A
F
E
D
C
B
9或10或18
M
N
(M)
(N)
M
N
A
F
E
D
C
B
MN=18
MN=9
A
F
E
D
C
B
M
N
MN=10
N
M
考点2-1
中考真题
双动点的分类讨论(一定两动)
MN=
6 3
9<MN<
6 3
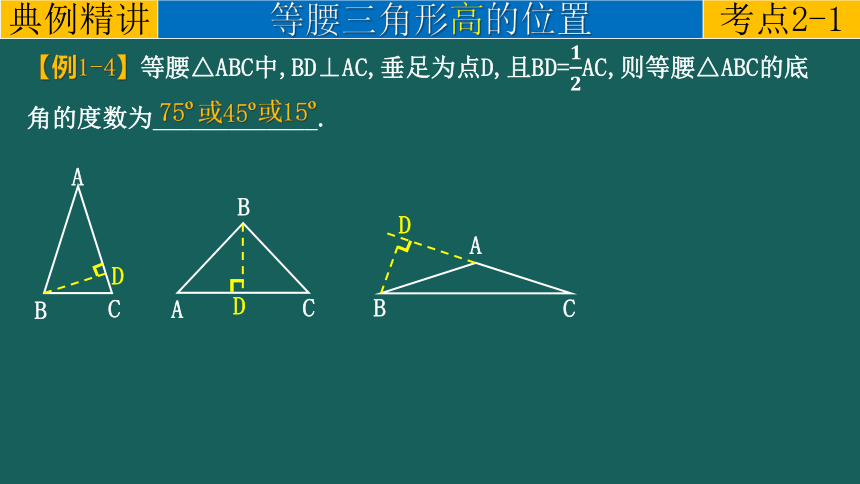
【例1-4】等腰△ABC中,BD⊥AC,垂足为点D,且BD=AC,则等腰△ABC的底角的度数为_____________.
75
C
B
A
A
C
B
B
C
A
或45
或15
D
D
D
考点2-1
典例精讲
等腰三角形高的位置
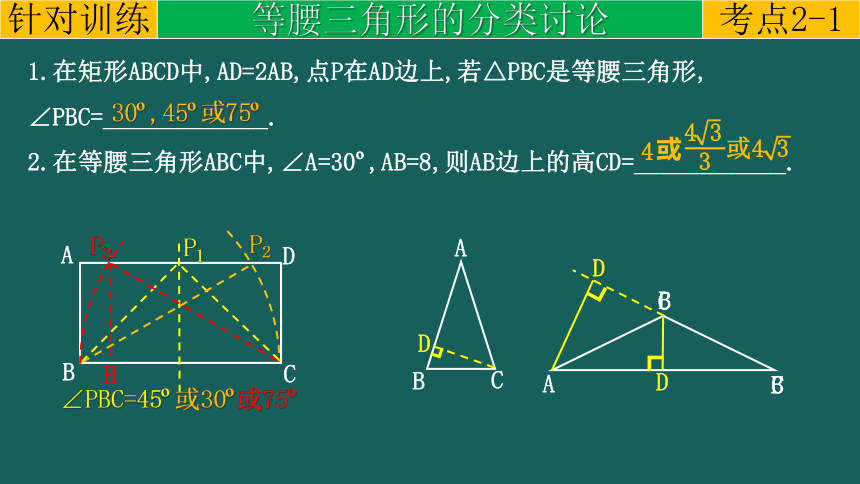
1.在矩形ABCD中,AD=2AB,点P在AD边上,若△PBC是等腰三角形,
∠PBC=_____________.
2.在等腰三角形ABC中,∠A=30 ,AB=8,则AB边上的高CD=____________.
A
C
B
D
P1
P2
P3
H
30 ,45 或75
∠PBC=45
或30
或75
考点2-1
针对训练
等腰三角形的分类讨论
或4 3
4
A
C
B
D
D
A
B
C
D
B
C
4 3
3
或
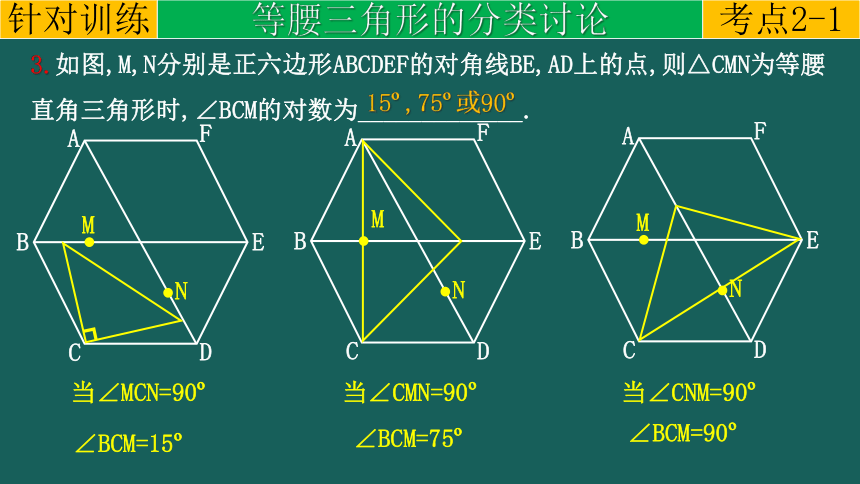
3.如图,M,N分别是正六边形ABCDEF的对角线BE,AD上的点,则△CMN为等腰直角三角形时,∠BCM的对数为_____________.
A
F
E
D
C
B
M
N
∠BCM=15
A
F
E
D
C
B
M
N
当∠MCN=90
当∠CMN=90
∠BCM=75
A
F
E
D
C
B
M
N
当∠CNM=90
∠BCM=90
15 ,75 或90
考点2-1
针对训练
等腰三角形的分类讨论
直线y=kx+2过点A(2,4),交x轴于点B,点P是坐标轴上一点,△PAB是直角三角形,则点P的坐标_______________________________________________.
A
P1
P3
y
x
O
B
P6
P5
P4
P2
(0,-2)
或(0,2-2 2)
或(0,2+2 2)
或(0,6)
或(2,0)
或(6,0)
考点2-2
理论依据
直角三角形的分类讨论(两定一动)
①以定点为直角顶点---作两条垂线
②以动点为直角顶点---作圆
【例2-1】(2015·T14)如图,在△ABC中,AB=BC=4,AO=BO,P是射线CO上的一个动点,∠AOC=60 ,当△PAB为直角三角形时,AP的长为______________.
A
C
B
O
P2
P3
A
C
B
O
P1
或2 3
2 7
或2
考点2-2
中考真题
直角三角形的分类讨论(两定一动)
【例2-2】(2019·T12)在平面直角坐标系中,A,B,C三点的坐标分别为(4,0),(4,4),(0,4),点P在x轴上,点D在直线AB上,若DA=1,CP⊥DP于点P,则点P的坐标为____________________________.
C
B
A
y
x
O
D1
D2
P1
P2
P3
(2,0)
或(2- ,0)
2 2
或(2+ ,0)
2 2
考点2-2
中考真题
直角三角形的分类讨论(两定一动)
1.如图,在□ABCD中,AD=10,tanB=2,AE⊥BC于点E,且AE=4cm,点P是BC边上一动点,若△PAD是直角三角形,则BP的长为_________cm.
考点2-2
针对训练
直角三角形的分类讨论(两定一动)
P2
P1
A
D
C
B
P3
2,4或10
2.如图,在平面直角坐标系中,点C(0,4),射线CE∥x轴,直线y=x+b交线段OC于点B,交x轴于于点A,D是射线CE上一点,若存在点D,使得△ABD恰为等腰直角三角形,则b的值为_________.
y
O
x
C
E
A
B
H
H
4
3
8
3
或
或2
D
D
D
考点2-2
针对训练
直角三角形的分类讨论(两定一动)
提升能力
强化训练
等腰三角形的分类讨论(两定一动)
1.在Rt△ABC中,∠ACB=90 ,AC=6,BC=8,点M为斜边AB的中点,点P是射线CM上一动点,若△PBC是等腰三角形,则CP的长为___________.
2.如图,在平面直角坐标系中,矩形OABC的顶点A,C的坐标分别为(10,0),
(0,4),D是OA的中点,点P在BC边上运动,当△ODP为腰长为5的等腰三角形时,点P的坐标为__________________.
5
A
C
B
M
(P1)
P2
P3
或8
或
64
5
(2,4),(3,4),(8,4)
C
x
y
D
O
B
A
P
P1
P2
P3
3.如图,在Rt△ABC中,∠ACB=90 ,∠B=30 ,AC=4,点D为AB的中点,点E在Rt△ABC的直角边上,若以C,D,E为顶点的三角形是直角三角形,则BE的长为_______________.
4.如图,点A(0,8),点B(4,0),连接AB,点M、N分别是OA,AB的中点,在射线MN上有一动点P.若△ABP是直角三角形,则点P的坐标是_______________.
E2
E3
E1
提升能力
强化训练
直角三角形的分类讨论(两定一动)
或2 3
或2 13
4
3
3
A
D
C
B
y
x
A
M
B
O
N
P
P
H
P
H
Q
(12,4)
或(2 5+2,4)
1.△ABC中,AB=AC=15,∠B=30 ,点D在AB上,过点D作DE∥BC交AC于点E,在BC上取一点F,使BD=DF,要使△DEF,△CEF均是等腰三角形,则AD的长为__________________.
A
C
B
A
C
B
A
C
B
①当DF=EF=EC时
D
E
F
D
F
E
D
F
E
x
x
x
x
x
②当DE=EF=FC时
x
3x
3x
③当DE=DF,CE=CF时
x
AD=
AD=
AD=
3x
3x
3x
3x
15
2
15
2
或
或
15 3-15
2
15
2
15
2
15 3-15
2
拓展思维
培优训练
等腰三角形的分类讨论
= 4-2
2.如图,在矩形ABCD中,AB=,AD=2,点E是BC边上的一个动点,连接AE,过点D作DF⊥AE于点F,当BE的长为_____________时,△CDF为等腰三角形.
A
F
E
C
D
B
G
N
M
①当DF=DC= 时,
2
2
或1
或2- 2
拓展思维
培优训练
等腰三角形的分类讨论
∴AF=
= 2,
过点F作MN∥BC,
∴AM=MF=1
∴△AMF∽△ABE
AM
AB
=
MF
BE
∴
AD2-DF2
∴BE=
2
②当CF=CD= 时,
2
过点C作CG⊥DF于点H,交AD于点G,
∴DH=HF,
H
∵DF⊥AE,
∴GH∥AF,
∴AG=DG=1,
∴CE=1,
∴BE=1,
③当FD=FC时,
过点F作MN∥BC,
∴DN=CN=AM=MB= ,
2
2
∴△AMF∽△FND
∴MF·FN=AM·DN=
1
2
∵MF+FN=2
∴MF=
2- 2
2
∴BE=2MF=
2- 2
3.如图,矩形ABCD中,AB=1,AD=2,E是AD的中点,P在射线BD上运动,若△BEP为等腰三角形,则线段BP的长度等于_____________.
A
E
C
D
B
P1
P2
P3
2
或
5
3
或
6 5
5
拓展思维
培优训练
等腰三角形的分类讨论
4.如图,已知点A(2,0),⊙A的半径为1,OB切⊙A于点B,点P为⊙A上的动点,当△POB是等腰三角形时,点P的坐标为______________________.
5.等腰三角形ABC中,顶角A为40 ,点P在以A为圆心,BC长为半径的圆上,且BP=BA,则∠PBC的度数为__________.
y
A
B
O
x
(1,0)
或(3,0)
或( , )
3
2
3
2
P1
P2
P3
30 或110
A
P
P
C
B
拓展思维
培优训练
等腰三角形的分类讨论
6.如图,在Rt△ABC中,∠A=90 ,AB=6,AC=8,D、E分别是AB、AC的中点,点P是BC边上一点,若△DEP是直角三角形,则BP=______________.
A
P
E
D
C
B
P1
P2
P3
P4
34
5
9
5
或
或
18
5
或5
拓展思维
培优训练
直角三角形的分类讨论
7.已知tan∠MON=3,点P在∠MON内,PC⊥ON,PC=1,OC=3,直线l绕点P旋转,交射线OM于点A,交射线ON于点B,当△AOB为直角三角形时,线段OA的长度为____________.
A
B
l
M
N
O
P
C
A
B
A
B
3 10
5
或3 10
拓展思维
培优训练
直角三角形的分类讨论
8.如图,∠MAN=90 ,点C在AM上,AC=4,点B为边AN上一动点,连接BC,△A BC与△ABC关于BC所在直线对称.点D,E分别为AC,BC的中点,连接DE并延长,交A B所在直线于点F,连接A E.当△A EF为直角三角形时,AB的长为________.
A
M
C
D
N
A
B
F
B
A
E
M
C
D
N
A
B
F
A
E
Q
P
4 3或4
拓展思维
培优训练
直角三角形的分类讨论
9.如图,在坐标系中,点A(0,2),B(-2,0),点D是x轴上一个动点,且△ABD为等腰三角形,以AD为一直角边在右侧作等腰直角△ADE,∠DAE=90 .则点E的坐标为_________________________________.
y
O
x
B
A
(D1)
E1
y
O
x
B
A
D2
E2
y
O
x
B
A
D3
E3
y
O
x
B
A
D4
E4
(2,2)
或(2,4)
或(2,2 2)
或(2,-2 2)
拓展思维
培优训练
直角三角形的分类讨论
10.已知菱形ABCD中,AB=5,cos∠ABC=,AE⊥CD,垂足为E,点P在对角线BD上,当△APE是直角三角形时,其斜边长为__________.
F
B
A
C
D
E
(P1)
(P2)
(P3)
(P4)
4或5或 41
拓展思维
培优训练
直角三角形的分类讨论
专题七 客观题的解题技巧
人教版中考第二轮总复习---几何模型
§7.3(1) 填空多解题
---特殊三角形的分类讨论
考点归纳
知识梳理
题型概述
填空多解题是近几年中考的常题型,这类试题综合性较强,在解答时需要灵活运用分类讨论和数形结合的数学思想方法求解,解题时常因考虑不全或不严谨,导致漏解、错解,所以考生必须熟练掌握这一题型的特征与解法.
分类讨论是重要的数学思想,也是重要的解题策略,很多数学问题很难从整体上去解决,若将其划分为几个局部问题,逐个予以解决.
基本方法:
①确定讨论对象以及所讨论对象的全体范围;
②确定分类标准,合理分类,即标准统一、不重不漏、分类互斥;
③对各个分类逐步进行讨论,分层进行,获取阶段性结果;
④最后进行归纳总结,综合得出结论.
如图,点A的坐标为(2,1),在坐标轴上确定一点P,使△PAO是等腰三角形,则点P的坐标为________________________________________________.
A
O
x
y
P7
P8
P3
P2
P1
P4
P5
P6
考点2-1
理论依据
等腰三角形的分类讨论(两定一动)
(0, )
5
2
( ,0)
5
4
( ,0)
5
(0, )
- 5
( ,0)
- 5
(0, )
5
(4,0)
(0,2)
等腰三角形的分类讨论:
①以OA为腰---作⊙O和⊙A;
②以OA为底---作OA的垂直平分线.
求解方法:
1.利用勾股定理求解;
2.利用相似求解;
3.利用三角函数求解.
【例1-1】(2016·T12)如图,是一张长方形纸片ABCD,已知AB=8,AD=7,E为AB上一点,AE=5,现要剪下一张等腰三角形纸片(AEP),使点P落在长方形ABCD的某一条边上,则等腰三角形AEP的底边长是______________.
P1
P2
P3
D
E
B
A
C
或5 2
或4 5
5
考点2-1
中考真题
等腰三角形的分类讨论(两定一动)
y
O
x
A1
A2
(3,4)
(4,3)
y
O
x
A1
A2
(3,4)
(4,3)
y
O
x
【例1-2】(2022·T12)已知点A在反比例函数y=(x>0)的图象上,点B在x轴正半轴上,若△OAB为等腰三角形,且腰长为5,则AB的长为___________.
考点2-1
中考真题
等腰三角形的分类讨论(一定两动)
以O为圆心,5为半径画⊙O,交⊙O于点A1,A2.
A1
A2
(3,4)
(4,3)
B2
A1B1=A1O=5
B1
B1
AB=
2 5
H
B2
H
AB=
10
5
或2 5
或 10
OA1=OB1=5
OA2=OB2=5
A2B2=A2O=5
【例1-3】(2021·T12)如图,在边长为的正六边形ABCDEF中,连接BE、CF,其中点M,N分别为BE和CF上的动点若以M、N、D为顶点的三角形是等边三角形,且边长为整数,则该等边三角形的边长为___________.
A
F
E
D
C
B
9或10或18
M
N
(M)
(N)
M
N
A
F
E
D
C
B
MN=18
MN=9
A
F
E
D
C
B
M
N
MN=10
N
M
考点2-1
中考真题
双动点的分类讨论(一定两动)
MN=
6 3
9<MN<
6 3
【例1-4】等腰△ABC中,BD⊥AC,垂足为点D,且BD=AC,则等腰△ABC的底角的度数为_____________.
75
C
B
A
A
C
B
B
C
A
或45
或15
D
D
D
考点2-1
典例精讲
等腰三角形高的位置
1.在矩形ABCD中,AD=2AB,点P在AD边上,若△PBC是等腰三角形,
∠PBC=_____________.
2.在等腰三角形ABC中,∠A=30 ,AB=8,则AB边上的高CD=____________.
A
C
B
D
P1
P2
P3
H
30 ,45 或75
∠PBC=45
或30
或75
考点2-1
针对训练
等腰三角形的分类讨论
或4 3
4
A
C
B
D
D
A
B
C
D
B
C
4 3
3
或
3.如图,M,N分别是正六边形ABCDEF的对角线BE,AD上的点,则△CMN为等腰直角三角形时,∠BCM的对数为_____________.
A
F
E
D
C
B
M
N
∠BCM=15
A
F
E
D
C
B
M
N
当∠MCN=90
当∠CMN=90
∠BCM=75
A
F
E
D
C
B
M
N
当∠CNM=90
∠BCM=90
15 ,75 或90
考点2-1
针对训练
等腰三角形的分类讨论
直线y=kx+2过点A(2,4),交x轴于点B,点P是坐标轴上一点,△PAB是直角三角形,则点P的坐标_______________________________________________.
A
P1
P3
y
x
O
B
P6
P5
P4
P2
(0,-2)
或(0,2-2 2)
或(0,2+2 2)
或(0,6)
或(2,0)
或(6,0)
考点2-2
理论依据
直角三角形的分类讨论(两定一动)
①以定点为直角顶点---作两条垂线
②以动点为直角顶点---作圆
【例2-1】(2015·T14)如图,在△ABC中,AB=BC=4,AO=BO,P是射线CO上的一个动点,∠AOC=60 ,当△PAB为直角三角形时,AP的长为______________.
A
C
B
O
P2
P3
A
C
B
O
P1
或2 3
2 7
或2
考点2-2
中考真题
直角三角形的分类讨论(两定一动)
【例2-2】(2019·T12)在平面直角坐标系中,A,B,C三点的坐标分别为(4,0),(4,4),(0,4),点P在x轴上,点D在直线AB上,若DA=1,CP⊥DP于点P,则点P的坐标为____________________________.
C
B
A
y
x
O
D1
D2
P1
P2
P3
(2,0)
或(2- ,0)
2 2
或(2+ ,0)
2 2
考点2-2
中考真题
直角三角形的分类讨论(两定一动)
1.如图,在□ABCD中,AD=10,tanB=2,AE⊥BC于点E,且AE=4cm,点P是BC边上一动点,若△PAD是直角三角形,则BP的长为_________cm.
考点2-2
针对训练
直角三角形的分类讨论(两定一动)
P2
P1
A
D
C
B
P3
2,4或10
2.如图,在平面直角坐标系中,点C(0,4),射线CE∥x轴,直线y=x+b交线段OC于点B,交x轴于于点A,D是射线CE上一点,若存在点D,使得△ABD恰为等腰直角三角形,则b的值为_________.
y
O
x
C
E
A
B
H
H
4
3
8
3
或
或2
D
D
D
考点2-2
针对训练
直角三角形的分类讨论(两定一动)
提升能力
强化训练
等腰三角形的分类讨论(两定一动)
1.在Rt△ABC中,∠ACB=90 ,AC=6,BC=8,点M为斜边AB的中点,点P是射线CM上一动点,若△PBC是等腰三角形,则CP的长为___________.
2.如图,在平面直角坐标系中,矩形OABC的顶点A,C的坐标分别为(10,0),
(0,4),D是OA的中点,点P在BC边上运动,当△ODP为腰长为5的等腰三角形时,点P的坐标为__________________.
5
A
C
B
M
(P1)
P2
P3
或8
或
64
5
(2,4),(3,4),(8,4)
C
x
y
D
O
B
A
P
P1
P2
P3
3.如图,在Rt△ABC中,∠ACB=90 ,∠B=30 ,AC=4,点D为AB的中点,点E在Rt△ABC的直角边上,若以C,D,E为顶点的三角形是直角三角形,则BE的长为_______________.
4.如图,点A(0,8),点B(4,0),连接AB,点M、N分别是OA,AB的中点,在射线MN上有一动点P.若△ABP是直角三角形,则点P的坐标是_______________.
E2
E3
E1
提升能力
强化训练
直角三角形的分类讨论(两定一动)
或2 3
或2 13
4
3
3
A
D
C
B
y
x
A
M
B
O
N
P
P
H
P
H
Q
(12,4)
或(2 5+2,4)
1.△ABC中,AB=AC=15,∠B=30 ,点D在AB上,过点D作DE∥BC交AC于点E,在BC上取一点F,使BD=DF,要使△DEF,△CEF均是等腰三角形,则AD的长为__________________.
A
C
B
A
C
B
A
C
B
①当DF=EF=EC时
D
E
F
D
F
E
D
F
E
x
x
x
x
x
②当DE=EF=FC时
x
3x
3x
③当DE=DF,CE=CF时
x
AD=
AD=
AD=
3x
3x
3x
3x
15
2
15
2
或
或
15 3-15
2
15
2
15
2
15 3-15
2
拓展思维
培优训练
等腰三角形的分类讨论
= 4-2
2.如图,在矩形ABCD中,AB=,AD=2,点E是BC边上的一个动点,连接AE,过点D作DF⊥AE于点F,当BE的长为_____________时,△CDF为等腰三角形.
A
F
E
C
D
B
G
N
M
①当DF=DC= 时,
2
2
或1
或2- 2
拓展思维
培优训练
等腰三角形的分类讨论
∴AF=
= 2,
过点F作MN∥BC,
∴AM=MF=1
∴△AMF∽△ABE
AM
AB
=
MF
BE
∴
AD2-DF2
∴BE=
2
②当CF=CD= 时,
2
过点C作CG⊥DF于点H,交AD于点G,
∴DH=HF,
H
∵DF⊥AE,
∴GH∥AF,
∴AG=DG=1,
∴CE=1,
∴BE=1,
③当FD=FC时,
过点F作MN∥BC,
∴DN=CN=AM=MB= ,
2
2
∴△AMF∽△FND
∴MF·FN=AM·DN=
1
2
∵MF+FN=2
∴MF=
2- 2
2
∴BE=2MF=
2- 2
3.如图,矩形ABCD中,AB=1,AD=2,E是AD的中点,P在射线BD上运动,若△BEP为等腰三角形,则线段BP的长度等于_____________.
A
E
C
D
B
P1
P2
P3
2
或
5
3
或
6 5
5
拓展思维
培优训练
等腰三角形的分类讨论
4.如图,已知点A(2,0),⊙A的半径为1,OB切⊙A于点B,点P为⊙A上的动点,当△POB是等腰三角形时,点P的坐标为______________________.
5.等腰三角形ABC中,顶角A为40 ,点P在以A为圆心,BC长为半径的圆上,且BP=BA,则∠PBC的度数为__________.
y
A
B
O
x
(1,0)
或(3,0)
或( , )
3
2
3
2
P1
P2
P3
30 或110
A
P
P
C
B
拓展思维
培优训练
等腰三角形的分类讨论
6.如图,在Rt△ABC中,∠A=90 ,AB=6,AC=8,D、E分别是AB、AC的中点,点P是BC边上一点,若△DEP是直角三角形,则BP=______________.
A
P
E
D
C
B
P1
P2
P3
P4
34
5
9
5
或
或
18
5
或5
拓展思维
培优训练
直角三角形的分类讨论
7.已知tan∠MON=3,点P在∠MON内,PC⊥ON,PC=1,OC=3,直线l绕点P旋转,交射线OM于点A,交射线ON于点B,当△AOB为直角三角形时,线段OA的长度为____________.
A
B
l
M
N
O
P
C
A
B
A
B
3 10
5
或3 10
拓展思维
培优训练
直角三角形的分类讨论
8.如图,∠MAN=90 ,点C在AM上,AC=4,点B为边AN上一动点,连接BC,△A BC与△ABC关于BC所在直线对称.点D,E分别为AC,BC的中点,连接DE并延长,交A B所在直线于点F,连接A E.当△A EF为直角三角形时,AB的长为________.
A
M
C
D
N
A
B
F
B
A
E
M
C
D
N
A
B
F
A
E
Q
P
4 3或4
拓展思维
培优训练
直角三角形的分类讨论
9.如图,在坐标系中,点A(0,2),B(-2,0),点D是x轴上一个动点,且△ABD为等腰三角形,以AD为一直角边在右侧作等腰直角△ADE,∠DAE=90 .则点E的坐标为_________________________________.
y
O
x
B
A
(D1)
E1
y
O
x
B
A
D2
E2
y
O
x
B
A
D3
E3
y
O
x
B
A
D4
E4
(2,2)
或(2,4)
或(2,2 2)
或(2,-2 2)
拓展思维
培优训练
直角三角形的分类讨论
10.已知菱形ABCD中,AB=5,cos∠ABC=,AE⊥CD,垂足为E,点P在对角线BD上,当△APE是直角三角形时,其斜边长为__________.
F
B
A
C
D
E
(P1)
(P2)
(P3)
(P4)
4或5或 41
拓展思维
培优训练
直角三角形的分类讨论
同课章节目录
