专题8.1创新作图---常用作图技巧在多边形中的应用 课件(共27张PPT)中考数学二轮复习必会几何模型剖析(全国通用)
文档属性
| 名称 | 专题8.1创新作图---常用作图技巧在多边形中的应用 课件(共27张PPT)中考数学二轮复习必会几何模型剖析(全国通用) |  | |
| 格式 | pptx | ||
| 文件大小 | 6.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-25 11:00:35 | ||
图片预览






文档简介
(共27张PPT)
专题八 创新作图
人教版中考第二轮总复习---几何模型
8.1 “常用作图技巧”
在“多边形”中的应用
是区别于尺规作图的另一种作图方式,它是以无刻度直尺作为唯一的作图工具,综合运用图形的几何性质、基本定理、图形变换等进行分析、推理、归纳,寻找作图依据。
考点归纳
题型概述
创新作图
创新作图:
创新作图的主要作图类型有:
1.在三角形中作图; 2.在特殊的四边形中作图;
3.在正多边形中作图; 4.在圆中作图; 5.在网格中作图。
无刻度直尺只能用来画直线,不能测量长度.
①找点:_________________________________________;
两条线相交的是点
两点确定一条直线
按要求构造三角形、四边形、正多边形等
(线可以是直线也可以是曲线)
考点归纳
题型概述
创新作图
创新作图的主要的作图要求有:
创新作图的常用的作图技巧有:
②画线:_________________________________________;
③构图:_________________________________________.
利用三角形三线交于一点作图
01
利用平行四边形对角线作图
02
利用轴对称的性质作图
03
知识要点
精讲精练
目录
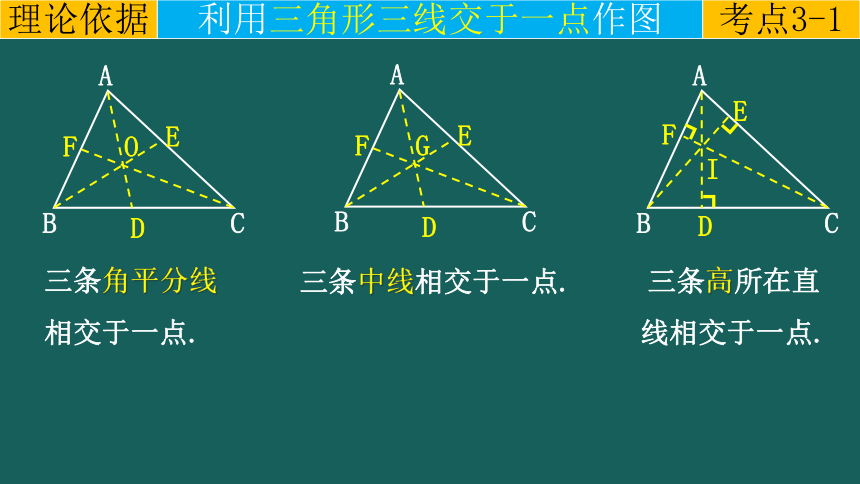
三条角平分线相交于一点.
A
C
B
A
C
B
三条高所在直线相交于一点.
三条中线相交于一点.
考点3-1
理论依据
利用三角形三线交于一点作图
E
F
D
O
A
C
B
E
F
D
G
E
F
D
I
【例1】如图,在正方形ABCD和正方形EFGH中,点B,G,F,C在同一条直线上,连接AF.请分别在下图中使用无刻度的直尺画图.
(1)如图1,点B与点G重合,过点C作CM⊥AF;
(2)如图2,点G在点B的左侧,过点C作CN⊥AF.
M
N
E
F
H
B(G)
C
D
A
图1
A
H
G
E
F
B
C
D
图2
∴CM即为所求;
∴CN即为所求;
考点3-1
典例精讲
利用三角形三线交于一点作图
利用三角形三线交于一点作图
01
利用平行四边形对角线作图
02
利用轴对称的性质作图
03
知识要点
精讲精练
目录
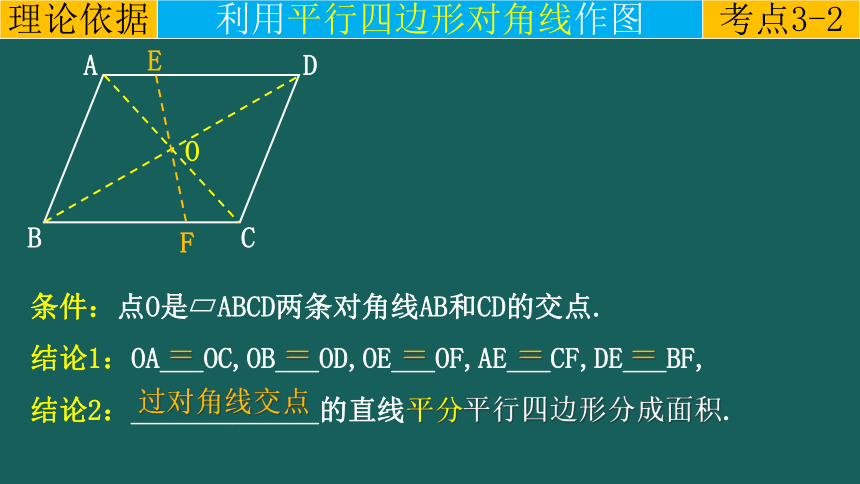
条件:点O是 ABCD两条对角线AB和CD的交点.
结论1:OA___OC,OB___OD,OE___OF,AE___CF,DE___BF,
结论2:_____________的直线平分平行四边形分成面积.
考点3-2
理论依据
利用平行四边形对角线作图
A
C
B
D
O
E
F
=
=
=
=
=
过对角线交点
图2
A
C
M
D
B
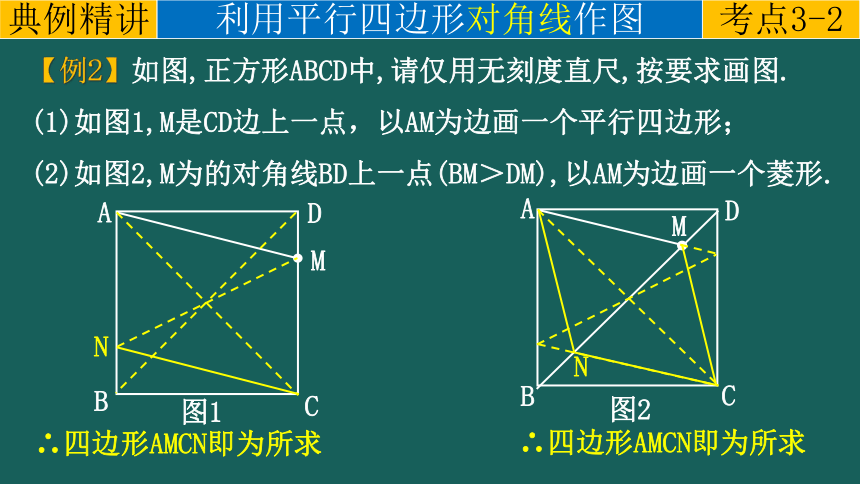
【例2】如图,正方形ABCD中,请仅用无刻度直尺,按要求画图.
(1)如图1,M是CD边上一点,以AM为边画一个平行四边形;
(2)如图2,M为的对角线BD上一点(BM>DM),以AM为边画一个菱形.
图1
A
C
M
D
B
N
∴四边形AMCN即为所求
N
∴四边形AMCN即为所求
考点3-2
典例精讲
利用平行四边形对角线作图
利用三角形三线交于一点作图
01
利用平行四边形对角线作图
02
利用轴对称的性质作图
03
知识要点
精讲精练
目录
考点3-3
理论依据
利用轴对称的性质作图
F
E
A
B
C
l
B
C
A
轴对称的性质3:如果对称边所在的直线相交,则交点一定在对称轴上.
M
N
E
E M
F N
=
C M
B N
由轴对称的性质可得:
CC ⊥l,BB ⊥l,CM=C M,BN=B N.
设EM=x,E M=y,
EM
EN
=
∴
EM
EN
=
E M
E N
∴
x
x+MN
=
y
y+MN
∴
∴CC ∥BB
CM
BN
,
∴x(y+MN)=y(x+MN)
∴xMN=yMN
∴x=y
∴E,E 重合
考点3-3
理论依据
利用轴对称的性质作图
E
轴对称的性质4:将两组对称点交叉相连,则交点一定在对称轴上.
A
B
C
l
B
C
A
F
E
N
M
O
B
C
C
B
M
N
CC
BB
=
EC
EB
∵CC∥BB
CM
BN
=
EC
EB
∴
∴△ECM∽△EBN,
CM
B N
=
CF
FB
△CMF∽△B NF,
△CC F∽△B BF,
CC
BB
=
CF
FB
△ECC ∽△EBB ,
CM
BN
=
CM
B N
∴
∴BN=B N
梯形四点共线:两腰延长线的交点,对角线的交点,上下两底的中点,四点在同一直线上;等腰梯形的外心也在这条直线(对称轴)上.
A
B
C
D
F
E
N
M
等腰
∴N 是BB 的中点.
图1
A
B
C
D
E
F
图2
B
C
D
A
E
H
∴EF即为所求;
∴BH即为所求;
【例3】在菱形ABCD中,BD为对角线,请仅用无刻度的直尺作图.
(1)在图1中,BE是△ABD的高,在AB上取一点F,使EF∥BD;
(2)在图2中,BE是△ABD的高,画出△BCD中CD边上的高BH.
考点3-3
典例精讲
利用轴对称的性质作图
中考真题
配套训练
常用作图技巧
A
图1
C
D
B
E
A
图2
C
D
B
E
1.(2018·T16)如图,在四边形ABCD中,AB∥CD,AB=2CD,E为AB的中点.请用无刻度的直尺分别按下列要求画图.
(1)在图1中,画出△ABD中BD边上的中线;
(2)在图2中,若BA=BD,画出△ABD中AD边上的高.
F
∴AF即为所求.
F
∴BF即为所求.
2.(2021·T16)已知正方形ABCD的边长为4个单位长度,点E是CD的中点,请仅用无刻度直尺完成以下作图(保留作图痕迹).(1)在图1中,将直线AC绕着正方形ABCD的中心顺时针旋转45 ;(2)在图2中,将直线AC向上平移1个单位长度.
A
E
C
D
B
图1
A
E
C
D
B
图2
O
F
∴OF即为所求;
A
E
C
D
B
图1
O
F
A
E
C
D
B
图1
O
F
M
N
A
E
C
D
B
图2
∴MN即为所求;
N
M
中考真题
配套训练
常用作图技巧
知识梳理
课堂小结
创新作图题
无刻度直尺作图常用的技巧
3.见轴对称图形(如角平分线、等腰三角形、等腰梯形、菱形、正方形、筝形等),_________________;
1.见中线、高、角平分线,_______________________;
利用三线相交于一点作图
2.见平行四边形(含菱形、矩形、正方形),_________;
连对角线
4.见平行且不相等的线段,______________________.
利用梯形四点共线作图
把对称点交叉相连
1.已知四边形ABCD,对角线AC垂直平分BD于点O,E,F分别是AB,AD的中点.请仅用无刻度的直尺分别在图①、图②中作出矩形EFPQ,使点P,Q分别在CD,BC上(保留作图痕迹,不写作法).
(1)如图①,OA=OC;(2)如图②,OA>OC.
A
O
C
F
E
D
B
图1
A
O
C
F
E
D
B
图2
Q
P
∴四边形EFPQ即为所求;
Q
P
∴四边形EFPQ即为所求;
查漏补缺
配套训练
常用作图技巧在多边形中的应用
2.点P是矩形ABCD边BC的中点,请仅用无刻度的直尺画图.
(1)在图1中画出AD的中点M;
(2)在图2中画出对角线AC的三等分点E,点F.
图1
A
P
D
C
B
图2
A
P
D
C
B
M
E
F
∴点M即为所求
∴点E、F即为所求
查漏补缺
配套训练
常用作图技巧在多边形中的应用
3.如图,△ABC≌△ADC,AM是∠BAC的角平分线,请仅用无刻度直尺,按要求画图.
(1)在图1中作出△ADC中∠DAC的角平分线AN;
(2)在图2中作出△AMC的高MH.
N
A
C
M
D
B
图1
H
A
M
C
D
B
图2
∴如图1,AN即为所求;
∴如图2,MH即为所求.
查漏补缺
配套训练
常用作图技巧在多边形中的应用
4.如图,四边形ABCD中,BC∥AD,BC=2AD,AB=CD.请仅用无刻度的直尺按要求画图.
(1)在图1中画出BC的中点E; (2)在图2中画出CD的中点F.
B
A
D
C
图1
B
A
D
C
图2
E
F
∴点E即为所求;
∴点F即为所求;
查漏补缺
配套训练
常用作图技巧在多边形中的应用
5.如图,在△ABC中,已知AB=AC,AD⊥BC于点D.请用无刻度的直尺分别按下列要求画图,
(1)如图1,点P为AB上任意一点,在AC上找出一点P ,使AP=AP ;
(2)如图2,点P为BC上任意一点,在CD上找出一点P ,使BP=CP ;
A
P
C
B
图1
D
P
A
P
C
B
图2
D
P
∴如图1,点P 即为所求;
∴如图2,点P 即为所求;
查漏补缺
配套训练
常用作图技巧在多边形中的应用
6.如图,△ABC与△BDE为全等的等边三角形,点A,B,D在同一直线上,请用无刻度的直尺画图.
(1)在图1中,过点B作直线BM与AD垂直;
(2)在图2中,作AB边的中点N.
图1
A
B
D
E
C
图2
A
B
D
E
C
M
M
图2
A
B
D
E
C
N
N
查漏补缺
配套训练
常用作图技巧在多边形中的应用
7.已知△ABC和△FDE都是等边三角形,点B、C、E、F在同一直线上,请用无刻度的直尺画图.
(1)在图1中,点C于点E重合,画出线段AD的中点P;
(2)在图2中,点E是线段BF的中点,画一条与AD相等的线段.
D
A
B
C(E)
F
图1
P
D
A
B
C
F
图2
E
M
查漏补缺
配套训练
常用作图技巧在多边形中的应用
图1
A
B
C
D
E
图2
A
B
C
D
E
8.如图,在菱形ABCD中,BD为对角线,请仅用无刻度的直尺作图.
(1)在图1中,BE是△BCD的中线,在AB上取一点F,使EF∥BC;
(2)在图2中,BE是△BCD的高,画出△BCD中BC边上的高DH.
F
H
查漏补缺
配套训练
常用作图技巧在多边形中的应用
9.在菱形ABCD中,AE⊥BC于E,请仅用无刻度的直尺作图.
(1)过点C在图1中画出AB边上的高;
(2)过点C在图2中画出AD边上的高.
F
F
A
B
C
D
E
图1
A
B
C
D
E
图2
如图1,CF就是AB边上的高
如图2,CF就是AD边上的高
查漏补缺
配套训练
常用作图技巧在多边形中的应用
10.已知矩形ABCD中,点F在AD边上,四边形EDCF是平行四边形.请仅用无刻度的直尺分别按下列要求画图.
(1)在图1中画一条线段PH,使PH=0.5ED.
(2)在图2中画出△BCD中DC边上的中线BM.
A
F
E
D
C
B
图1
A
F
E
D
C
B
图2
P
H
M
A
F
E
D
C
B
图1
H
P
查漏补缺
配套训练
常用作图技巧在多边形中的应用
11.已知正方形ABCD与正方形EFGB,点E在AB上,且为AB的中点,点G在线段BC的反向延长线上,请仅用无刻度直尺按下列要求画图.
(1)在图1中,画出AE的中点P;
(2)在图2中,画出BC的垂直平分线.
A
C
D
E
G
F
B
图1
A
C
D
E
G
F
B
图2
P
M
N
如图2,MN即为所求
查漏补缺
配套训练
常用作图技巧在多边形中的应用
专题八 创新作图
人教版中考第二轮总复习---几何模型
8.1 “常用作图技巧”
在“多边形”中的应用
是区别于尺规作图的另一种作图方式,它是以无刻度直尺作为唯一的作图工具,综合运用图形的几何性质、基本定理、图形变换等进行分析、推理、归纳,寻找作图依据。
考点归纳
题型概述
创新作图
创新作图:
创新作图的主要作图类型有:
1.在三角形中作图; 2.在特殊的四边形中作图;
3.在正多边形中作图; 4.在圆中作图; 5.在网格中作图。
无刻度直尺只能用来画直线,不能测量长度.
①找点:_________________________________________;
两条线相交的是点
两点确定一条直线
按要求构造三角形、四边形、正多边形等
(线可以是直线也可以是曲线)
考点归纳
题型概述
创新作图
创新作图的主要的作图要求有:
创新作图的常用的作图技巧有:
②画线:_________________________________________;
③构图:_________________________________________.
利用三角形三线交于一点作图
01
利用平行四边形对角线作图
02
利用轴对称的性质作图
03
知识要点
精讲精练
目录
三条角平分线相交于一点.
A
C
B
A
C
B
三条高所在直线相交于一点.
三条中线相交于一点.
考点3-1
理论依据
利用三角形三线交于一点作图
E
F
D
O
A
C
B
E
F
D
G
E
F
D
I
【例1】如图,在正方形ABCD和正方形EFGH中,点B,G,F,C在同一条直线上,连接AF.请分别在下图中使用无刻度的直尺画图.
(1)如图1,点B与点G重合,过点C作CM⊥AF;
(2)如图2,点G在点B的左侧,过点C作CN⊥AF.
M
N
E
F
H
B(G)
C
D
A
图1
A
H
G
E
F
B
C
D
图2
∴CM即为所求;
∴CN即为所求;
考点3-1
典例精讲
利用三角形三线交于一点作图
利用三角形三线交于一点作图
01
利用平行四边形对角线作图
02
利用轴对称的性质作图
03
知识要点
精讲精练
目录
条件:点O是 ABCD两条对角线AB和CD的交点.
结论1:OA___OC,OB___OD,OE___OF,AE___CF,DE___BF,
结论2:_____________的直线平分平行四边形分成面积.
考点3-2
理论依据
利用平行四边形对角线作图
A
C
B
D
O
E
F
=
=
=
=
=
过对角线交点
图2
A
C
M
D
B
【例2】如图,正方形ABCD中,请仅用无刻度直尺,按要求画图.
(1)如图1,M是CD边上一点,以AM为边画一个平行四边形;
(2)如图2,M为的对角线BD上一点(BM>DM),以AM为边画一个菱形.
图1
A
C
M
D
B
N
∴四边形AMCN即为所求
N
∴四边形AMCN即为所求
考点3-2
典例精讲
利用平行四边形对角线作图
利用三角形三线交于一点作图
01
利用平行四边形对角线作图
02
利用轴对称的性质作图
03
知识要点
精讲精练
目录
考点3-3
理论依据
利用轴对称的性质作图
F
E
A
B
C
l
B
C
A
轴对称的性质3:如果对称边所在的直线相交,则交点一定在对称轴上.
M
N
E
E M
F N
=
C M
B N
由轴对称的性质可得:
CC ⊥l,BB ⊥l,CM=C M,BN=B N.
设EM=x,E M=y,
EM
EN
=
∴
EM
EN
=
E M
E N
∴
x
x+MN
=
y
y+MN
∴
∴CC ∥BB
CM
BN
,
∴x(y+MN)=y(x+MN)
∴xMN=yMN
∴x=y
∴E,E 重合
考点3-3
理论依据
利用轴对称的性质作图
E
轴对称的性质4:将两组对称点交叉相连,则交点一定在对称轴上.
A
B
C
l
B
C
A
F
E
N
M
O
B
C
C
B
M
N
CC
BB
=
EC
EB
∵CC∥BB
CM
BN
=
EC
EB
∴
∴△ECM∽△EBN,
CM
B N
=
CF
FB
△CMF∽△B NF,
△CC F∽△B BF,
CC
BB
=
CF
FB
△ECC ∽△EBB ,
CM
BN
=
CM
B N
∴
∴BN=B N
梯形四点共线:两腰延长线的交点,对角线的交点,上下两底的中点,四点在同一直线上;等腰梯形的外心也在这条直线(对称轴)上.
A
B
C
D
F
E
N
M
等腰
∴N 是BB 的中点.
图1
A
B
C
D
E
F
图2
B
C
D
A
E
H
∴EF即为所求;
∴BH即为所求;
【例3】在菱形ABCD中,BD为对角线,请仅用无刻度的直尺作图.
(1)在图1中,BE是△ABD的高,在AB上取一点F,使EF∥BD;
(2)在图2中,BE是△ABD的高,画出△BCD中CD边上的高BH.
考点3-3
典例精讲
利用轴对称的性质作图
中考真题
配套训练
常用作图技巧
A
图1
C
D
B
E
A
图2
C
D
B
E
1.(2018·T16)如图,在四边形ABCD中,AB∥CD,AB=2CD,E为AB的中点.请用无刻度的直尺分别按下列要求画图.
(1)在图1中,画出△ABD中BD边上的中线;
(2)在图2中,若BA=BD,画出△ABD中AD边上的高.
F
∴AF即为所求.
F
∴BF即为所求.
2.(2021·T16)已知正方形ABCD的边长为4个单位长度,点E是CD的中点,请仅用无刻度直尺完成以下作图(保留作图痕迹).(1)在图1中,将直线AC绕着正方形ABCD的中心顺时针旋转45 ;(2)在图2中,将直线AC向上平移1个单位长度.
A
E
C
D
B
图1
A
E
C
D
B
图2
O
F
∴OF即为所求;
A
E
C
D
B
图1
O
F
A
E
C
D
B
图1
O
F
M
N
A
E
C
D
B
图2
∴MN即为所求;
N
M
中考真题
配套训练
常用作图技巧
知识梳理
课堂小结
创新作图题
无刻度直尺作图常用的技巧
3.见轴对称图形(如角平分线、等腰三角形、等腰梯形、菱形、正方形、筝形等),_________________;
1.见中线、高、角平分线,_______________________;
利用三线相交于一点作图
2.见平行四边形(含菱形、矩形、正方形),_________;
连对角线
4.见平行且不相等的线段,______________________.
利用梯形四点共线作图
把对称点交叉相连
1.已知四边形ABCD,对角线AC垂直平分BD于点O,E,F分别是AB,AD的中点.请仅用无刻度的直尺分别在图①、图②中作出矩形EFPQ,使点P,Q分别在CD,BC上(保留作图痕迹,不写作法).
(1)如图①,OA=OC;(2)如图②,OA>OC.
A
O
C
F
E
D
B
图1
A
O
C
F
E
D
B
图2
Q
P
∴四边形EFPQ即为所求;
Q
P
∴四边形EFPQ即为所求;
查漏补缺
配套训练
常用作图技巧在多边形中的应用
2.点P是矩形ABCD边BC的中点,请仅用无刻度的直尺画图.
(1)在图1中画出AD的中点M;
(2)在图2中画出对角线AC的三等分点E,点F.
图1
A
P
D
C
B
图2
A
P
D
C
B
M
E
F
∴点M即为所求
∴点E、F即为所求
查漏补缺
配套训练
常用作图技巧在多边形中的应用
3.如图,△ABC≌△ADC,AM是∠BAC的角平分线,请仅用无刻度直尺,按要求画图.
(1)在图1中作出△ADC中∠DAC的角平分线AN;
(2)在图2中作出△AMC的高MH.
N
A
C
M
D
B
图1
H
A
M
C
D
B
图2
∴如图1,AN即为所求;
∴如图2,MH即为所求.
查漏补缺
配套训练
常用作图技巧在多边形中的应用
4.如图,四边形ABCD中,BC∥AD,BC=2AD,AB=CD.请仅用无刻度的直尺按要求画图.
(1)在图1中画出BC的中点E; (2)在图2中画出CD的中点F.
B
A
D
C
图1
B
A
D
C
图2
E
F
∴点E即为所求;
∴点F即为所求;
查漏补缺
配套训练
常用作图技巧在多边形中的应用
5.如图,在△ABC中,已知AB=AC,AD⊥BC于点D.请用无刻度的直尺分别按下列要求画图,
(1)如图1,点P为AB上任意一点,在AC上找出一点P ,使AP=AP ;
(2)如图2,点P为BC上任意一点,在CD上找出一点P ,使BP=CP ;
A
P
C
B
图1
D
P
A
P
C
B
图2
D
P
∴如图1,点P 即为所求;
∴如图2,点P 即为所求;
查漏补缺
配套训练
常用作图技巧在多边形中的应用
6.如图,△ABC与△BDE为全等的等边三角形,点A,B,D在同一直线上,请用无刻度的直尺画图.
(1)在图1中,过点B作直线BM与AD垂直;
(2)在图2中,作AB边的中点N.
图1
A
B
D
E
C
图2
A
B
D
E
C
M
M
图2
A
B
D
E
C
N
N
查漏补缺
配套训练
常用作图技巧在多边形中的应用
7.已知△ABC和△FDE都是等边三角形,点B、C、E、F在同一直线上,请用无刻度的直尺画图.
(1)在图1中,点C于点E重合,画出线段AD的中点P;
(2)在图2中,点E是线段BF的中点,画一条与AD相等的线段.
D
A
B
C(E)
F
图1
P
D
A
B
C
F
图2
E
M
查漏补缺
配套训练
常用作图技巧在多边形中的应用
图1
A
B
C
D
E
图2
A
B
C
D
E
8.如图,在菱形ABCD中,BD为对角线,请仅用无刻度的直尺作图.
(1)在图1中,BE是△BCD的中线,在AB上取一点F,使EF∥BC;
(2)在图2中,BE是△BCD的高,画出△BCD中BC边上的高DH.
F
H
查漏补缺
配套训练
常用作图技巧在多边形中的应用
9.在菱形ABCD中,AE⊥BC于E,请仅用无刻度的直尺作图.
(1)过点C在图1中画出AB边上的高;
(2)过点C在图2中画出AD边上的高.
F
F
A
B
C
D
E
图1
A
B
C
D
E
图2
如图1,CF就是AB边上的高
如图2,CF就是AD边上的高
查漏补缺
配套训练
常用作图技巧在多边形中的应用
10.已知矩形ABCD中,点F在AD边上,四边形EDCF是平行四边形.请仅用无刻度的直尺分别按下列要求画图.
(1)在图1中画一条线段PH,使PH=0.5ED.
(2)在图2中画出△BCD中DC边上的中线BM.
A
F
E
D
C
B
图1
A
F
E
D
C
B
图2
P
H
M
A
F
E
D
C
B
图1
H
P
查漏补缺
配套训练
常用作图技巧在多边形中的应用
11.已知正方形ABCD与正方形EFGB,点E在AB上,且为AB的中点,点G在线段BC的反向延长线上,请仅用无刻度直尺按下列要求画图.
(1)在图1中,画出AE的中点P;
(2)在图2中,画出BC的垂直平分线.
A
C
D
E
G
F
B
图1
A
C
D
E
G
F
B
图2
P
M
N
如图2,MN即为所求
查漏补缺
配套训练
常用作图技巧在多边形中的应用
同课章节目录
