专题8.2创新作图---常用作图技巧在圆中的应用 课件(共21张PPT)-中考数学二轮复习必会几何模型剖析(全国通用)
文档属性
| 名称 | 专题8.2创新作图---常用作图技巧在圆中的应用 课件(共21张PPT)-中考数学二轮复习必会几何模型剖析(全国通用) |

|
|
| 格式 | pptx | ||
| 文件大小 | 6.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-25 00:00:00 | ||
图片预览






文档简介
(共21张PPT)
专题八 创新作图
人教版中考第二轮总复习---几何模型
8.2 “常用作图技巧”
在“圆”中的应用
是区别于尺规作图的另一种作图方式,它是以无刻度直尺作为唯一的作图工具,综合运用图形的几何性质、基本定理、图形变换等进行分析、推理、归纳,寻找作图依据。
考点归纳
题型概述
创新作图
创新作图:
创新作图的主要作图类型有:
1.在三角形中作图; 2.在特殊的四边形中作图;
3.在正多边形中作图; 4.在圆中作图; 5.在网格中作图。
无刻度直尺只能用来画直线,不能测量长度.
①找点:_________________________________________;
两条线相交的是点
两点确定一条直线
按要求构造三角形、四边形、正多边形等
(线可以是直线也可以是曲线)
考点归纳
题型概述
创新作图
创新作图的主要的作图要求有:
创新作图的常用的作图技巧有:
②画线:_________________________________________;
③构图:_________________________________________.
(确定圆心、弧的中点)
(作切线、直径、垂直平分线)
利用三角形三线交于一点作图
01
利用平行四边形对角线作图
02
利用轴对称的性质作图
03
知识要点
精讲精练
目录
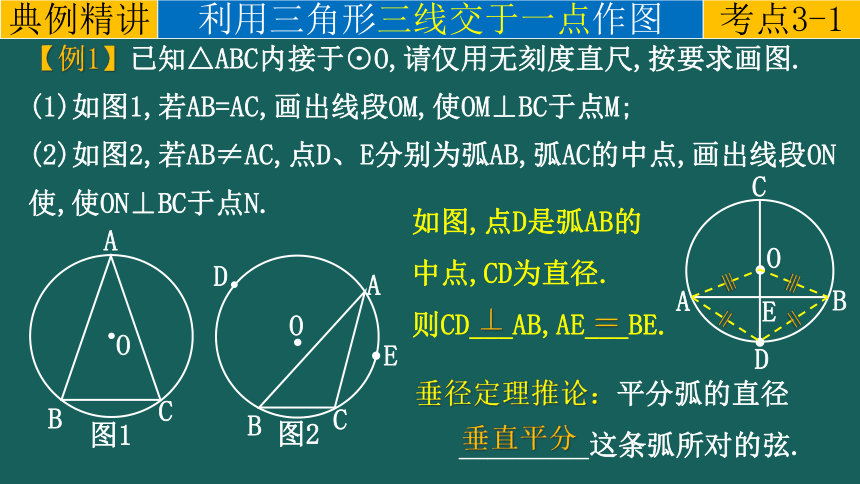
【例1】已知△ABC内接于⊙O,请仅用无刻度直尺,按要求画图.
(1)如图1,若AB=AC,画出线段OM,使OM⊥BC于点M;
(2)如图2,若AB≠AC,点D、E分别为弧AB,弧AC的中点,画出线段ON使,使ON⊥BC于点N.
A
B
C
O
图1
图2
A
B
C
O
E
D
考点3-1
典例精讲
利用三角形三线交于一点作图
A
B
O
D
E
C
如图,点D是弧AB的中点,CD为直径.
则CD___AB,AE___BE.
=
⊥
垂径定理推论:平分弧的直径
_________这条弧所对的弦.
≡
=
=
≡
垂直平分
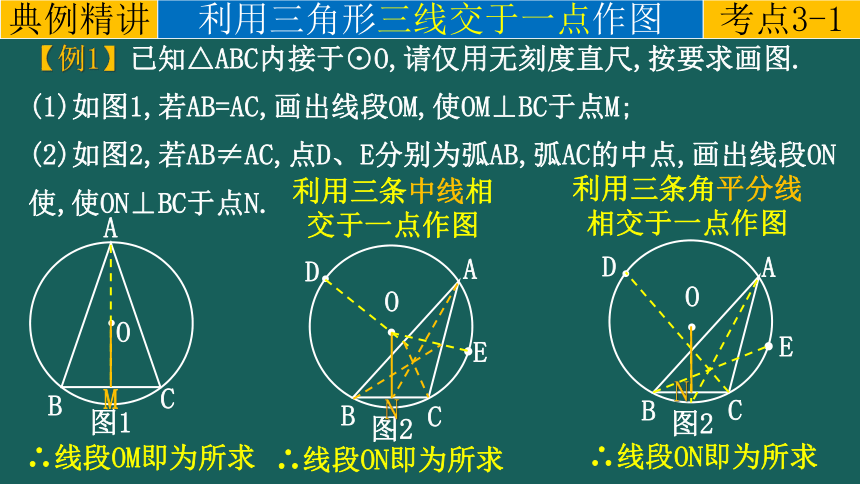
【例1】已知△ABC内接于⊙O,请仅用无刻度直尺,按要求画图.
(1)如图1,若AB=AC,画出线段OM,使OM⊥BC于点M;
(2)如图2,若AB≠AC,点D、E分别为弧AB,弧AC的中点,画出线段ON使,使ON⊥BC于点N.
A
B
C
O
图1
考点3-1
典例精讲
利用三角形三线交于一点作图
M
∴线段OM即为所求
图2
A
B
C
O
E
D
N
∴线段ON即为所求
利用三条中线相交于一点作图
图2
A
B
C
O
E
D
N
∴线段ON即为所求
利用三条角平分线相交于一点作图
利用三角形三线交于一点作图
01
利用平行四边形对角线作图
02
利用轴对称的性质作图
03
知识要点
精讲精练
目录
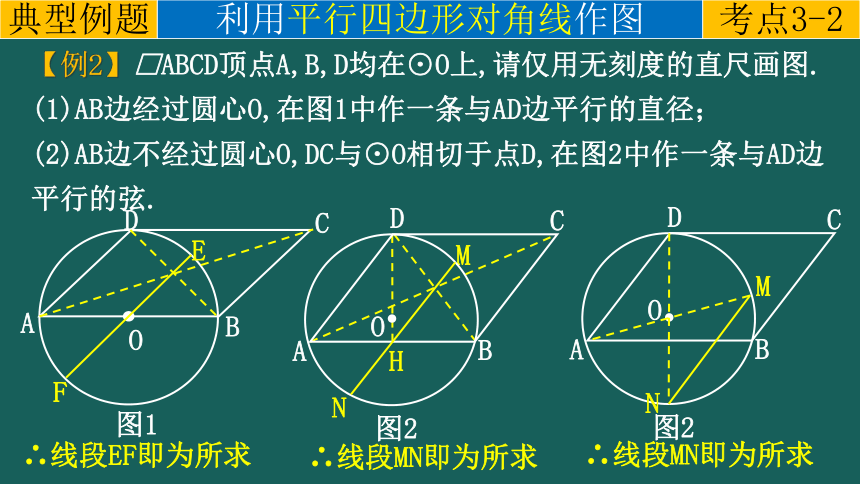
【例2】□ABCD顶点A,B,D均在⊙O上,请仅用无刻度的直尺画图.
(1)AB边经过圆心O,在图1中作一条与AD边平行的直径;
(2)AB边不经过圆心O,DC与⊙O相切于点D,在图2中作一条与AD边平行的弦.
∴线段EF即为所求
A
C
O
B
D
图1
E
F
考点3-2
典型例题
利用平行四边形对角线作图
M
N
∴线段MN即为所求
A
C
O
B
D
图2
H
A
C
O
B
D
图2
M
N
∴线段MN即为所求
利用三角形三线交于一点作图
01
利用平行四边形对角线作图
02
利用轴对称的性质作图
03
知识要点
精讲精练
目录
【例3】如图,圆上四点A,B,C,D且AB∥CD,仅用无刻度的直尺画图.
(1)图1,画出弦AB的中点E;
(2)图2,若AB为直径,在圆上找到M,N两点,使四边形CDMN为矩形.
E
B
A
D
C
图1
A
D
C
B
图2
O
M
N
如图1,点E即为所求
如图2,四边形CDMN即为所求
考点3-3
典型例题
利用轴对称的性质作图
(2013·T16)如图AB是半圆的直径,图1中,点C在半圆外;图2中,点C在半圆内,请仅用无刻度的直尺按要求画图.
(1)在图1中,画出△ABC的三条高的交点;
(2)在图2中,画出△ABC中AB边上的高.
H
D
A
B
图1
C
A
C
B
图2
如图1,点D即为所求
如图2,CH即为所求
中考真题
配套训练
利用三角形三线交于一点作图
知识梳理
课堂小结
创新作图题
无刻度直尺作图常用的技巧
3.见轴对称图形(如等腰三角形,菱形,正方形,筝形等),
_________________;
1.见中线,高,角平分线,垂直平分线,_______________________;
利用三线相交于一点作图
2.见平行四边形(含菱形,矩形,正方形),__________;
连对角线
4.见平行且不相等的线段,______________________.
利用梯形四点共线作图
把对称点交叉相连
1.如图,△ABC内接于⊙O,AB=AC,D是弧AC的中点.请分别在下图中使用无刻度的直尺画图.
(1)在图1中,画出△ABC的AC边上的中线BE;
(2)在图2中,画出△ABC的AB边上的中线CF。
B
A
C
O
D
图1
E
如图1,BE即为所求
F
D
B
O
C
A
图2
如图2,CF即为所求.
查漏补缺
配套训练
常用作图技巧在圆中的应用
2.请仅用无刻度的直尺,用连线的方法在图1、图2中分别过圆外一点A画出直径BC所在直线的垂线.
D
E
F
M
B
C
A
图1
B
C
A
图2
如图1,AD即为所求
如图2,AD即为所求
查漏补缺
配套训练
常用作图技巧在圆中的应用
3.如图,在△ABC中,AB=BC,O为AB的中点,以OA为半径画弧,与AC相交于D,连接BD;请仅用无刻度的直尺作图,
(1)在图①中找到BC的中点M;
(2)在图②中过点D,作直线l∥AB.
A
C
O
B
D
图1
M
A
C
O
B
D
图2
l
如图1,点M即为所求
如图2,直线l即为所求
查漏补缺
配套训练
常用作图技巧在圆中的应用
4.已知BC是⊙的直径,△ABC为等腰三角形,且BC为底边,请用无刻度的直尺完成下列作图.
(1)在图1中,点A在圆上,画出正方形ABDC;
(2)在图2中,点A在圆外,画出菱形ABDC.
C
B
O
图1
A
C
B
O
图2
A
D
D
查漏补缺
配套训练
常用作图技巧在圆中的应用
5.在图1、图2中,四边形ABCD为矩形,某圆经过A,B两点,请仅用无刻度的直尺画出符合要求的图形.
(1)在图1中画出圆心O;(2)在图2中画出线段CD的垂直平分线.
O
E
F
如图1,点O即为所求
如图2,EF即为所求
B
A
C
D
图1
B
A
C
D
图2
查漏补缺
配套训练
常用作图技巧在圆中的应用
6.已知AB为⊙O的直径,点M、N为⊙O上关于AB成轴对称的两个点,仅用无刻度的直尺完成下列作图.
(1)如图1,点P为⊙O上异于A,B的任意一点,过点P作AB的垂线;
(2)如图2,过圆心O作AB的垂线.
B
A
M
O
图1
P
N
Q
如图1,PQ即为所求.
B
A
M
O
图2
N
如图2,PO即为所求.
P
查漏补缺
配套训练
常用作图技巧在圆中的应用
7.如图,AB是⊙O的直径,□ABCD的一边在直径AB上,点在⊙O上,请你仅用无刻度的直尺按下列要求作图.
(1)如图1,当点D在⊙O上时,在AB上取点P,使DP⊥AB于P;
(2)如图2,当点D在⊙O内时,在AB上取点Q,使EQ⊥AB于Q;
B
A
O
图1
D
E
C
P
要作互余的角或垂直关系想到直径所对的圆周角是90
B
A
O
图2
D
E
C
Q
查漏补缺
配套训练
常用作图技巧在圆中的应用
8.如图,四边形BCDE为菱形,其中E为AB的中点,C,D在以AB为直径的半圆上.请用两种不同的方法找到弧CD的中点(仅用无刻度的直尺作图)
E
D
C
A
B
图1
E
D
C
A
B
图2
F
如图1,点F即为所求
F
如图2,点F即为所求
查漏补缺
配套训练
常用作图技巧在圆中的应用
9.如图,已知圆为四边形ABCD的外接圆,且AB//CD,请仅用无刻度的直尺,根据下列条件分别在图1、图2中画出一条直线,这条直线同时将四边形ABCD和圆分成面积相等的两部分.
(1)如图1,AB经过圆心; (2)如图2,AB不经过圆心.
如图1中直线m为所求;
如图2中直线n为所求.
m
n
A
D
C
O
B
图1
A
D
C
B
图2
查漏补缺
配套训练
常用作图技巧在圆中的应用
专题八 创新作图
人教版中考第二轮总复习---几何模型
8.2 “常用作图技巧”
在“圆”中的应用
是区别于尺规作图的另一种作图方式,它是以无刻度直尺作为唯一的作图工具,综合运用图形的几何性质、基本定理、图形变换等进行分析、推理、归纳,寻找作图依据。
考点归纳
题型概述
创新作图
创新作图:
创新作图的主要作图类型有:
1.在三角形中作图; 2.在特殊的四边形中作图;
3.在正多边形中作图; 4.在圆中作图; 5.在网格中作图。
无刻度直尺只能用来画直线,不能测量长度.
①找点:_________________________________________;
两条线相交的是点
两点确定一条直线
按要求构造三角形、四边形、正多边形等
(线可以是直线也可以是曲线)
考点归纳
题型概述
创新作图
创新作图的主要的作图要求有:
创新作图的常用的作图技巧有:
②画线:_________________________________________;
③构图:_________________________________________.
(确定圆心、弧的中点)
(作切线、直径、垂直平分线)
利用三角形三线交于一点作图
01
利用平行四边形对角线作图
02
利用轴对称的性质作图
03
知识要点
精讲精练
目录
【例1】已知△ABC内接于⊙O,请仅用无刻度直尺,按要求画图.
(1)如图1,若AB=AC,画出线段OM,使OM⊥BC于点M;
(2)如图2,若AB≠AC,点D、E分别为弧AB,弧AC的中点,画出线段ON使,使ON⊥BC于点N.
A
B
C
O
图1
图2
A
B
C
O
E
D
考点3-1
典例精讲
利用三角形三线交于一点作图
A
B
O
D
E
C
如图,点D是弧AB的中点,CD为直径.
则CD___AB,AE___BE.
=
⊥
垂径定理推论:平分弧的直径
_________这条弧所对的弦.
≡
=
=
≡
垂直平分
【例1】已知△ABC内接于⊙O,请仅用无刻度直尺,按要求画图.
(1)如图1,若AB=AC,画出线段OM,使OM⊥BC于点M;
(2)如图2,若AB≠AC,点D、E分别为弧AB,弧AC的中点,画出线段ON使,使ON⊥BC于点N.
A
B
C
O
图1
考点3-1
典例精讲
利用三角形三线交于一点作图
M
∴线段OM即为所求
图2
A
B
C
O
E
D
N
∴线段ON即为所求
利用三条中线相交于一点作图
图2
A
B
C
O
E
D
N
∴线段ON即为所求
利用三条角平分线相交于一点作图
利用三角形三线交于一点作图
01
利用平行四边形对角线作图
02
利用轴对称的性质作图
03
知识要点
精讲精练
目录
【例2】□ABCD顶点A,B,D均在⊙O上,请仅用无刻度的直尺画图.
(1)AB边经过圆心O,在图1中作一条与AD边平行的直径;
(2)AB边不经过圆心O,DC与⊙O相切于点D,在图2中作一条与AD边平行的弦.
∴线段EF即为所求
A
C
O
B
D
图1
E
F
考点3-2
典型例题
利用平行四边形对角线作图
M
N
∴线段MN即为所求
A
C
O
B
D
图2
H
A
C
O
B
D
图2
M
N
∴线段MN即为所求
利用三角形三线交于一点作图
01
利用平行四边形对角线作图
02
利用轴对称的性质作图
03
知识要点
精讲精练
目录
【例3】如图,圆上四点A,B,C,D且AB∥CD,仅用无刻度的直尺画图.
(1)图1,画出弦AB的中点E;
(2)图2,若AB为直径,在圆上找到M,N两点,使四边形CDMN为矩形.
E
B
A
D
C
图1
A
D
C
B
图2
O
M
N
如图1,点E即为所求
如图2,四边形CDMN即为所求
考点3-3
典型例题
利用轴对称的性质作图
(2013·T16)如图AB是半圆的直径,图1中,点C在半圆外;图2中,点C在半圆内,请仅用无刻度的直尺按要求画图.
(1)在图1中,画出△ABC的三条高的交点;
(2)在图2中,画出△ABC中AB边上的高.
H
D
A
B
图1
C
A
C
B
图2
如图1,点D即为所求
如图2,CH即为所求
中考真题
配套训练
利用三角形三线交于一点作图
知识梳理
课堂小结
创新作图题
无刻度直尺作图常用的技巧
3.见轴对称图形(如等腰三角形,菱形,正方形,筝形等),
_________________;
1.见中线,高,角平分线,垂直平分线,_______________________;
利用三线相交于一点作图
2.见平行四边形(含菱形,矩形,正方形),__________;
连对角线
4.见平行且不相等的线段,______________________.
利用梯形四点共线作图
把对称点交叉相连
1.如图,△ABC内接于⊙O,AB=AC,D是弧AC的中点.请分别在下图中使用无刻度的直尺画图.
(1)在图1中,画出△ABC的AC边上的中线BE;
(2)在图2中,画出△ABC的AB边上的中线CF。
B
A
C
O
D
图1
E
如图1,BE即为所求
F
D
B
O
C
A
图2
如图2,CF即为所求.
查漏补缺
配套训练
常用作图技巧在圆中的应用
2.请仅用无刻度的直尺,用连线的方法在图1、图2中分别过圆外一点A画出直径BC所在直线的垂线.
D
E
F
M
B
C
A
图1
B
C
A
图2
如图1,AD即为所求
如图2,AD即为所求
查漏补缺
配套训练
常用作图技巧在圆中的应用
3.如图,在△ABC中,AB=BC,O为AB的中点,以OA为半径画弧,与AC相交于D,连接BD;请仅用无刻度的直尺作图,
(1)在图①中找到BC的中点M;
(2)在图②中过点D,作直线l∥AB.
A
C
O
B
D
图1
M
A
C
O
B
D
图2
l
如图1,点M即为所求
如图2,直线l即为所求
查漏补缺
配套训练
常用作图技巧在圆中的应用
4.已知BC是⊙的直径,△ABC为等腰三角形,且BC为底边,请用无刻度的直尺完成下列作图.
(1)在图1中,点A在圆上,画出正方形ABDC;
(2)在图2中,点A在圆外,画出菱形ABDC.
C
B
O
图1
A
C
B
O
图2
A
D
D
查漏补缺
配套训练
常用作图技巧在圆中的应用
5.在图1、图2中,四边形ABCD为矩形,某圆经过A,B两点,请仅用无刻度的直尺画出符合要求的图形.
(1)在图1中画出圆心O;(2)在图2中画出线段CD的垂直平分线.
O
E
F
如图1,点O即为所求
如图2,EF即为所求
B
A
C
D
图1
B
A
C
D
图2
查漏补缺
配套训练
常用作图技巧在圆中的应用
6.已知AB为⊙O的直径,点M、N为⊙O上关于AB成轴对称的两个点,仅用无刻度的直尺完成下列作图.
(1)如图1,点P为⊙O上异于A,B的任意一点,过点P作AB的垂线;
(2)如图2,过圆心O作AB的垂线.
B
A
M
O
图1
P
N
Q
如图1,PQ即为所求.
B
A
M
O
图2
N
如图2,PO即为所求.
P
查漏补缺
配套训练
常用作图技巧在圆中的应用
7.如图,AB是⊙O的直径,□ABCD的一边在直径AB上,点在⊙O上,请你仅用无刻度的直尺按下列要求作图.
(1)如图1,当点D在⊙O上时,在AB上取点P,使DP⊥AB于P;
(2)如图2,当点D在⊙O内时,在AB上取点Q,使EQ⊥AB于Q;
B
A
O
图1
D
E
C
P
要作互余的角或垂直关系想到直径所对的圆周角是90
B
A
O
图2
D
E
C
Q
查漏补缺
配套训练
常用作图技巧在圆中的应用
8.如图,四边形BCDE为菱形,其中E为AB的中点,C,D在以AB为直径的半圆上.请用两种不同的方法找到弧CD的中点(仅用无刻度的直尺作图)
E
D
C
A
B
图1
E
D
C
A
B
图2
F
如图1,点F即为所求
F
如图2,点F即为所求
查漏补缺
配套训练
常用作图技巧在圆中的应用
9.如图,已知圆为四边形ABCD的外接圆,且AB//CD,请仅用无刻度的直尺,根据下列条件分别在图1、图2中画出一条直线,这条直线同时将四边形ABCD和圆分成面积相等的两部分.
(1)如图1,AB经过圆心; (2)如图2,AB不经过圆心.
如图1中直线m为所求;
如图2中直线n为所求.
m
n
A
D
C
O
B
图1
A
D
C
B
图2
查漏补缺
配套训练
常用作图技巧在圆中的应用
同课章节目录
