专题8.3创新作图---在网格线中作图-中考数学二轮复习必会几何模型剖析(全国通用)
文档属性
| 名称 | 专题8.3创新作图---在网格线中作图-中考数学二轮复习必会几何模型剖析(全国通用) |  | |
| 格式 | pptx | ||
| 文件大小 | 6.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-26 09:04:03 | ||
图片预览





文档简介
(共37张PPT)
专题八 创新作图
人教版中考第二轮总复习---几何模型
8.3 利用平移、旋转、轴对称、相似
在网格线中作图
是区别于尺规作图的另一种作图方式,它是以无刻度直尺作为唯一的作图工具,综合运用图形的几何性质、基本定理、图形变换等进行分析、推理、归纳,寻找作图依据。
考点归纳
题型概述
创新作图
创新作图:
创新作图的主要作图类型有:
1.在三角形中作图; 2.在特殊的四边形中作图;
3.在正多边形中作图; 4.在圆中作图; 5.在网格中作图。
无刻度直尺只能用来画直线,不能测量长度.
①找点:_________________________________________;
②画线:_________________________________________;
③构图:_________________________________________.
两条线相交的是点
两点确定一条直线
按要求构造三角形、四边形等
(线可以是直线也可以是曲线)
考点归纳
题型概述
创新作图
创新作图的主要的作图要求有:
创新作图的常用的作图技巧有:
A
B
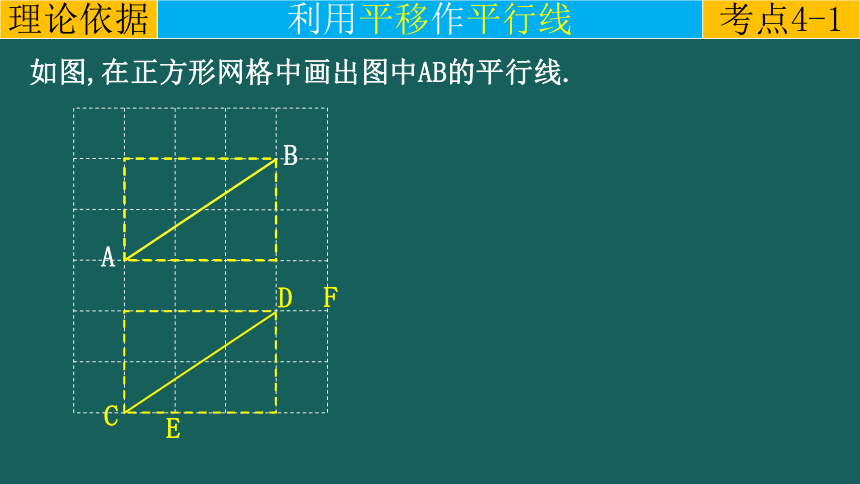
如图,在正方形网格中画出图中AB的平行线.
考点4-1
理论依据
利用平移作平行线
D
C
F
E
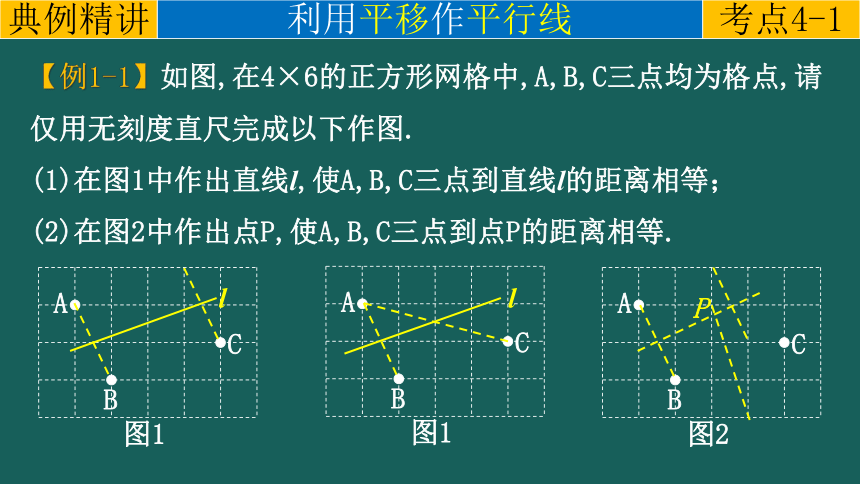
【例1-1】如图,在4×6的正方形网格中,A,B,C三点均为格点,请仅用无刻度直尺完成以下作图.
(1)在图1中作出直线l,使A,B,C三点到直线l的距离相等;
(2)在图2中作出点P,使A,B,C三点到点P的距离相等.
图1
A
B
C
l
图1
A
B
C
l
图2
A
B
C
P
考点4-1
典例精讲
利用平移作平行线
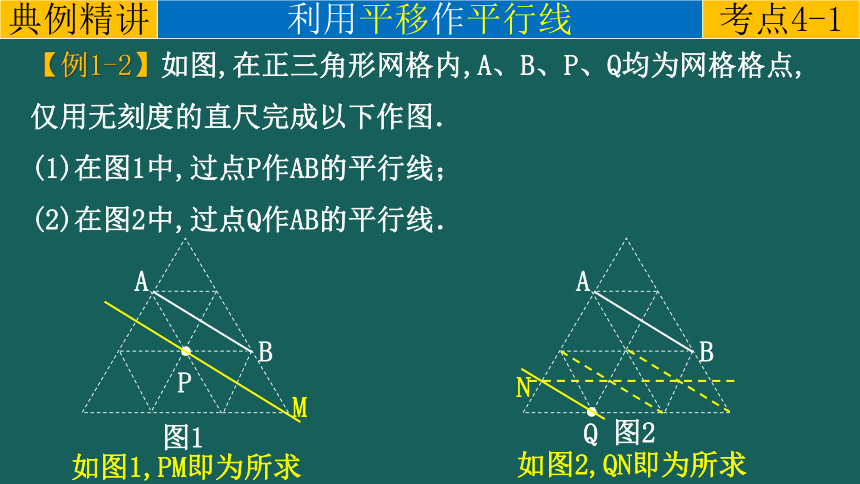
【例1-2】如图,在正三角形网格内,A、B、P、Q均为网格格点,仅用无刻度的直尺完成以下作图.
(1)在图1中,过点P作AB的平行线;
(2)在图2中,过点Q作AB的平行线.
A
B
P
图1
A
B
Q
图2
M
N
如图1,PM即为所求
如图2,QN即为所求
考点4-1
典例精讲
利用平移作平行线
如图,在正方形网格中分别画出图中AB的垂线和垂直平分线.
考点4-2
理论依据
利用旋转作垂线
A
B
C
E
F
A
B
C
D
A
C
B
图1
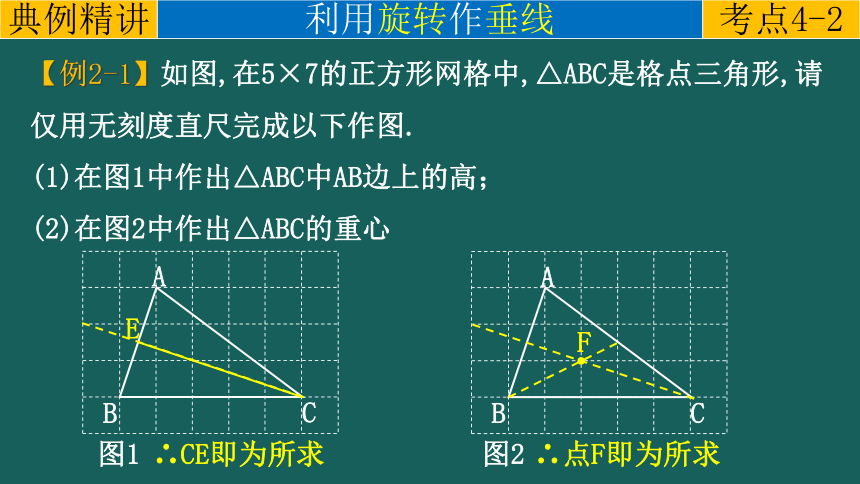
【例2-1】如图,在5×7的正方形网格中,△ABC是格点三角形,请仅用无刻度直尺完成以下作图.
(1)在图1中作出△ABC中AB边上的高;
(2)在图2中作出△ABC的重心
A
C
B
图2
E
∴CE即为所求
F
∴点F即为所求
考点4-2
典例精讲
利用旋转作垂线
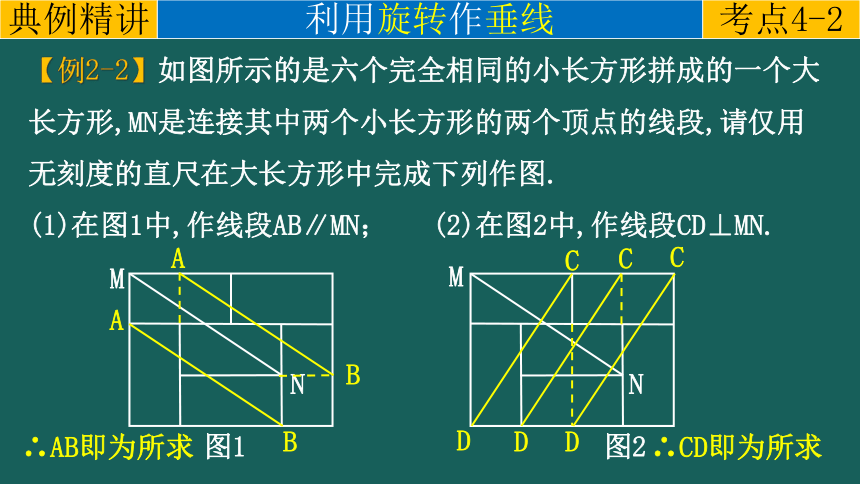
【例2-2】如图所示的是六个完全相同的小长方形拼成的一个大长方形,MN是连接其中两个小长方形的两个顶点的线段,请仅用无刻度的直尺在大长方形中完成下列作图.
(1)在图1中,作线段AB∥MN; (2)在图2中,作线段CD⊥MN.
图1
M
N
图2
N
M
A
B
A
B
C
D
C
D
D
C
∴AB即为所求
∴CD即为所求
考点4-2
典例精讲
利用旋转作垂线
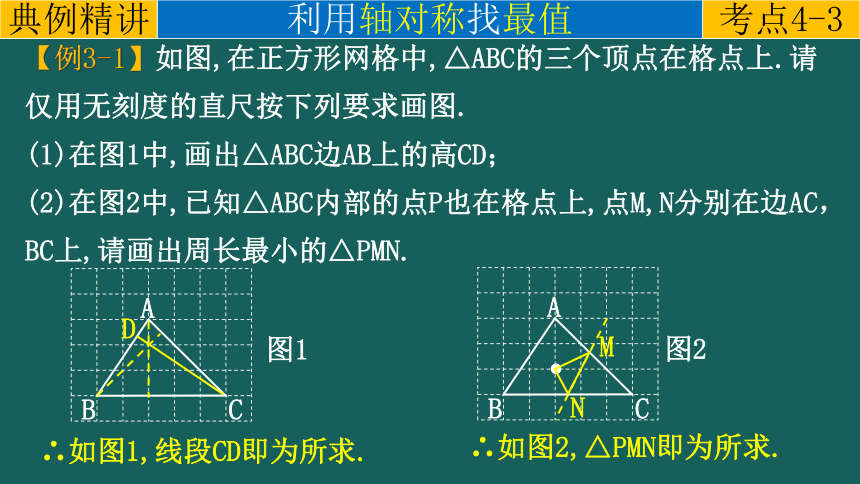
【例3-1】如图,在正方形网格中,△ABC的三个顶点在格点上.请仅用无刻度的直尺按下列要求画图.
(1)在图1中,画出△ABC边AB上的高CD;
(2)在图2中,已知△ABC内部的点P也在格点上,点M,N分别在边AC,BC上,请画出周长最小的△PMN.
∴如图2,△PMN即为所求.
图1
A
C
B
D
∴如图1,线段CD即为所求.
图2
A
C
B
M
N
考点4-3
典例精讲
利用轴对称找最值
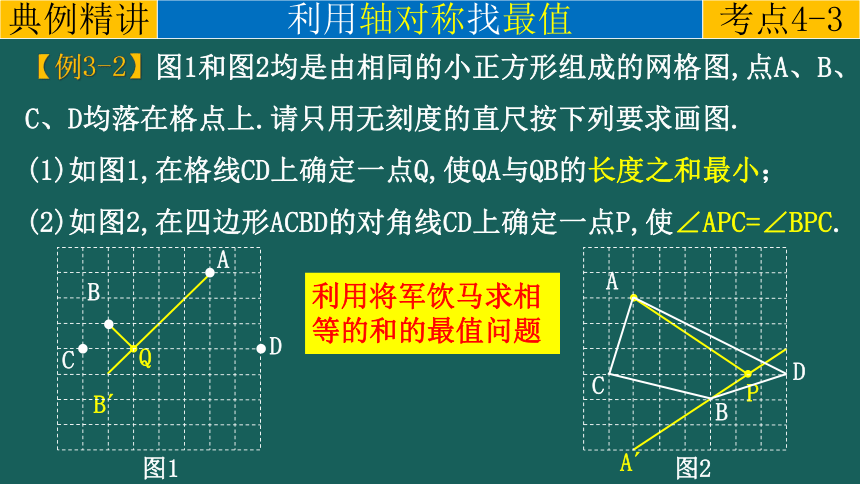
【例3-2】图1和图2均是由相同的小正方形组成的网格图,点A、B、C、D均落在格点上.请只用无刻度的直尺按下列要求画图.
(1)如图1,在格线CD上确定一点Q,使QA与QB的长度之和最小;
(2)如图2,在四边形ACBD的对角线CD上确定一点P,使∠APC=∠BPC.
利用将军饮马求相等的和的最值问题
Q
B
P
A
A
B
C
D
图1
A
C
B
D
图2
考点4-3
典例精讲
利用轴对称找最值
如图,在线段AB上找一点P,使AP:PB=3:2
A
B
考点4-4
理论依据
利用相似等分线段
P
P
A
B
P
P
利用“8(X)字形”相似作图
利用“A字形”相似作图
【例4-1】△ABC顶点均在网格的格点上,仅用无刻度的直尺作图.
(1)在图1中的线段AB上找一点D,连接CD,使S△ACD=S△ABC;
(2)在图2中的线段AB上找一点E,连接CE,使S△ACE=S△ABC;
图2
A
B
C
图1
A
B
C
D
E
∴△ACD即为所求
∴△ACE即为所求
考点4-4
典例精讲
利用相似等分线段
【例4-2】在正方形网格中,△ABC的三个顶点均在格点上,请仅用无刻度直尺,分别按下列要求画出线段EF.
(1)在图1中,点E,F分别在AB,AC上,EF∥BC且EF=BC;
(2)在图2中,点E,F分别在AB,AC上,EF∥BC且EF=BC.
A
C
B
图1
E
F
A
C
B
图2
E
F
∴EF即为所求
∴EF即为所求
考点4-4
典例精讲
利用相似等分线段
A
B
C
D
如图2
A
B
C
D
如图1
1.(2014·T17)已知梯形ABCD,请使用无刻度直尺画一个与梯形ABCD面积相等的图形.
(1)在图1中,画以CD为边的三角形;
(2)在图2中,画以AB为边的平行四边形.
E
F
E
如图1,△CDE即为所求;
如图2,□ABEF即为所求.
中考真题
配套训练
在网格线中作图
2.(2016·T17)如图,六个完全相同的小长方形拼成一个大长方形,AB是其中一个小长方形的对角线,请在大长方形中完成下列画图,要求:
1.仅用无刻度直尺;2.保留必要的画图痕迹.
(1)在图1中画一个45 角,使点A或点B是这个角的顶点,AB为这个角的一边.
(2)在图2中画出线段AB的垂直平分线.
图2
A
B
C
图1
A
B
如图1,∠BAC即为所求
如图2,EF即为所求
E
F
中考真题
配套训练
在网格线中作图
3.(2020·T16)如图,在正方形网格中,△ABC的顶点在格点上,请仅用无刻度直尺完成以下作图(保留作图痕迹).
(1)在图1中,作△ABC关于点O对称的△A B C ;
(2)在图2中,作△ABC绕点A顺时针旋转一定角度后,顶点仍在格点上的△A B C .
O
图1
A
C
B
图2
A
C
B
A
B
C
C
B
中考真题
配套训练
在网格线中作图
4.(2022 T16)如图是4×4的正方形网格,请仅用无刻度的直尺按要求完成以下作图(保留作图痕迹).
(1)在图1中作∠ABC的角平分线;
(2)在图2中过点C作一条直线l,使点A,B到直线l的距离相等.
C
A
B
图1
C
A
B
图2
D
∴BD即为所求
D
∴l即为所求
C
A
B
图2
D
l
l
∴l即为所求
中考真题
配套训练
在网格线中作图
5.(2023 T14)如图是4×4的正方形网格,请仅用无刻度的直尺按要求完成以下作图(保留作图痕迹).
(1)在图1中作锐角△ABC,使点C在格点上;
(2)在图2中的线段AB上作点Q,使PQ最短.
B
A
图1
B
A
图2
P
C1
C2
C3
C4
C5
C6
Q
∴△ABC即为所求
∴PQ即为所求
中考真题
配套训练
在网格线中作图
1.利用平移作平行线;
4.利用相似等分线段。
知识梳理
课堂小结
在网格线中作图
2.利用旋转作垂线;
3.利用轴对称找最值;
1.如图,在5×5的正方形网格中,△ABC顶点均为格点,请仅用无刻度直尺完成以下作图.
(1)在图1中,作出△ABC的高AM;
(2)在图2中,作出△ABC的高AN.
图1
C
B
A
图2
C
A
B
M
N
查漏补缺
配套训练
在网格线中作图
2.如图,在6×6的正方形网格中,△ABC的顶点在格点上,请仅用无刻度的直尺分别在图①、图②中画出△ABC的AB边上的高.
H
H
D
∴CH就是AB边上的高
∴CH就是AB边上的高
A
C
B
图1
A
B
C
图2
查漏补缺
配套训练
在网格线中作图
3.如图是4×4的网格,请仅用无刻度直尺完成以下作图.
(1)如图1,点A,B均在格点上,请过点A画出与AB垂直的直线AF;
(2)如图2,点A,B,C,D均在格点上,E是AC与BD的交点,请画出∠AEB的平分线EG.
A
B
图2
E
D
A
B
图1
G
C
∴EG即为所求
查漏补缺
配套训练
在网格线中作图
4.如图,在6×6的正方形网格中,等腰△ABC的顶点A,B在格点上,顶角∠A=36 ,请仅用无刻度直尺完成以下作图.
(1)在图1中,作△ABC的中线CD;
(2)在图2中,作△ABC的角平分线BE.
图1
A
C
B
图2
A
C
B
D
E
查漏补缺
配套训练
在网格线中作图
5.如图,在6×6的网格线中,四边形ABCD的顶点,点E都在格点上,仅用无刻度的直尺按下列要求作图.
(1)在图1中,作出△ABE关于直线l对称的△A1B1E1;
(2)如图2,在OC上找出点F,使EA平分∠BEF.
图1
A
E
B
O
l
图2
A
E
B
C
O
E1
(A1)
(B1)
F
△A1B1E1即为所求;
点F即为所求.
图2
A
E
B
C
O
F
点F即为所求.
查漏补缺
配套训练
在网格线中作图
6.利用网格和无刻度直尺按要求画图.
(1)如图1,在线段AB上找一点P,使AP=4BP;
(2)在图2中画出一条线段AB,使得AB=;
A
B
图1
P
图2
A
B
∴点P即为所求
∴AB即为所求
查漏补缺
配套训练
在网格线中作图
7.如图,在9×6的正方形网格中,点A,B,C均在格点(小正方形的顶点)上.请仅用无刻度的直尺按要求作图.
(1)在图1中,作格点D(不在直线BC上),使∠DBA=∠CBA;
(2)在图2中,E为AC上一点,在△ABC的内部作点P,使∠APB=∠APE.
∴如图2,点P即为所求.
图1
A
C
B
图2
A
E
C
B
D
∴如图1,点D即为所求.
P
查漏补缺
配套训练
在网格线中作图
8.如图,由6个形状,大小完全相同的小矩形组成大矩形网格,小矩形的顶点称为这个矩形网格的格点,请仅用无刻度直尺在矩形中完成下列画图.
(1)在图1中画出一个顶点均在格点上的非特殊的平行四边形;
(2)在图2中画出一个顶点均在格点上的非特殊的菱形.
图1
图2
D
A
B
C
A
B
C
D
如图1,四边形ABCD即为所求;
如图2,四边形ABCD即为所求.
查漏补缺
配套训练
在网格线中作图
提升能力
强化训练
在网格线中作图
A
B
1.如图,在由长为2,宽为1的矩形组成的网格中,已知A、B都是格点.请仅用无刻度的直尺在大长方形中完成下列作图.
(1)在图1中,画出线段AB的垂直平分线MN;
(2)在图2中,线段CD∥AB,画出线段CD的中点O.
A
B
C
D
O
N
M
利用梯形
四点共线作图
利用轴对称的性质作图
2.如图,射线OA放置在小正方形组成的网格中,现请你分别在图1,图2,图3中画射线OB,使tan∠AOB的值分别为1,,.
以OA为直角边
0
A
图1
B
B
B
0
A
图2
B
以OA为斜边
B
B
提升能力
强化训练
在网格线中作图
提升能力
强化训练
在网格线中作图
3.如图,是由小正方形组成的9×6网格,每个小正方形的顶点叫做格点.△ABC的顶点都是格点.仅用无刻度的直尺按下列要求作图.
(1)在图1中,D,E分别是边AB,AC与网格线的交点.在AC上画点G,使DG∥BC.
(2)在图2中,P是边AB上一点,∠BAC=α.先将AB绕点A逆时针旋转2α,得到线段AH,画出线段AH,再画点Q,使P,Q两点关于直线AC对称.
图1
A
D
C
B
图2
A
P
C
B
G
H
Q
4.如图,在边长为1个单位长度的小正方形组成的7×7的网格中,线段AB的端点为格点.仅用无刻度的直尺作图.
(1)在图1中,以线段AB为边作一个非正方形的菱形ABCD(点C,D也为格点)
(2)在图2中,以线段AB为底的等腰△PAB,(点P不一定为格点).
A
B
图1
A
B
图2
D
C
P
提升能力
强化训练
在网格线中作图
5.在6×6的正方形网格中,格点A,B在网格中的位置如图所示.请用无刻度直尺按要求画图.
(1)在图1中,画一个以A,B为顶点,另两个顶点也在格点上的正方形.
(2)在图2中,画一个以A,B为顶点,另两个顶点也在格点上的菱形,且使这个菱形的面积最小.
A
B
图1
A
B
图2
D
C
D
C
提升能力
强化训练
在网格线中作图
6.在下列6×6的正方形网格中,若每一个小正方形的边长均为1,请用无刻度直尺按要求画图:
(1)在图1中,以AB为边画一个正方形ABCD;
(2)在图2中,以AB为边画一个面积为5的矩形ABCD.
B
A
B
A
D
C
C
D
图1
图2
提升能力
强化训练
在网格线中作图
7.在10×10的正方形网格中,线段AB在网格中的位置如图所示,请用无刻度直尺按要求画图.
(1)在图1中,画菱形ABCD,且顶点C,D也在格点上;
(2)在图2中,画面积最大的菱形ABCD,且顶点C,D也在格点上.
与图形面积有关的作图
提升能力
强化训练
在网格线中作图
C
D
A
B
图1
A
B
图2
C
D
D
C
8.如图,在4×4的菱形网格图中(小菱形的边长为1,有一个角是60 ),请用无刻度直尺画顶点均落在格点上的面积最大的图形.
(1)在图1中画一个直角三角形;
(2)在图2中画一个四条边均不在网格线上的矩形.
图1
C
B
A
图2
A
C
D
B
提升能力
强化训练
在网格线中作图
A
B
C
图
2
A
B
C
图
1
9.如图,在8×6的正方形网格中,线段AB、BC的端点均在小正方形的顶点上,请仅用无刻度的直尺画图.
(1)在图1中找一点D(点D在小正方形的顶点上),连接AD、BD、CD,使△ABD与△BCD全等;
(2)在图2中找一点E(点E在格点上),使△ABE与△BCE均为以BE为直角边的直角三角形,且其中一个三角形的面积是另一个三角形面积的2倍.
与图形面积有关的作图
D
E
提升能力
强化训练
在网格线中作图
专题八 创新作图
人教版中考第二轮总复习---几何模型
8.3 利用平移、旋转、轴对称、相似
在网格线中作图
是区别于尺规作图的另一种作图方式,它是以无刻度直尺作为唯一的作图工具,综合运用图形的几何性质、基本定理、图形变换等进行分析、推理、归纳,寻找作图依据。
考点归纳
题型概述
创新作图
创新作图:
创新作图的主要作图类型有:
1.在三角形中作图; 2.在特殊的四边形中作图;
3.在正多边形中作图; 4.在圆中作图; 5.在网格中作图。
无刻度直尺只能用来画直线,不能测量长度.
①找点:_________________________________________;
②画线:_________________________________________;
③构图:_________________________________________.
两条线相交的是点
两点确定一条直线
按要求构造三角形、四边形等
(线可以是直线也可以是曲线)
考点归纳
题型概述
创新作图
创新作图的主要的作图要求有:
创新作图的常用的作图技巧有:
A
B
如图,在正方形网格中画出图中AB的平行线.
考点4-1
理论依据
利用平移作平行线
D
C
F
E
【例1-1】如图,在4×6的正方形网格中,A,B,C三点均为格点,请仅用无刻度直尺完成以下作图.
(1)在图1中作出直线l,使A,B,C三点到直线l的距离相等;
(2)在图2中作出点P,使A,B,C三点到点P的距离相等.
图1
A
B
C
l
图1
A
B
C
l
图2
A
B
C
P
考点4-1
典例精讲
利用平移作平行线
【例1-2】如图,在正三角形网格内,A、B、P、Q均为网格格点,仅用无刻度的直尺完成以下作图.
(1)在图1中,过点P作AB的平行线;
(2)在图2中,过点Q作AB的平行线.
A
B
P
图1
A
B
Q
图2
M
N
如图1,PM即为所求
如图2,QN即为所求
考点4-1
典例精讲
利用平移作平行线
如图,在正方形网格中分别画出图中AB的垂线和垂直平分线.
考点4-2
理论依据
利用旋转作垂线
A
B
C
E
F
A
B
C
D
A
C
B
图1
【例2-1】如图,在5×7的正方形网格中,△ABC是格点三角形,请仅用无刻度直尺完成以下作图.
(1)在图1中作出△ABC中AB边上的高;
(2)在图2中作出△ABC的重心
A
C
B
图2
E
∴CE即为所求
F
∴点F即为所求
考点4-2
典例精讲
利用旋转作垂线
【例2-2】如图所示的是六个完全相同的小长方形拼成的一个大长方形,MN是连接其中两个小长方形的两个顶点的线段,请仅用无刻度的直尺在大长方形中完成下列作图.
(1)在图1中,作线段AB∥MN; (2)在图2中,作线段CD⊥MN.
图1
M
N
图2
N
M
A
B
A
B
C
D
C
D
D
C
∴AB即为所求
∴CD即为所求
考点4-2
典例精讲
利用旋转作垂线
【例3-1】如图,在正方形网格中,△ABC的三个顶点在格点上.请仅用无刻度的直尺按下列要求画图.
(1)在图1中,画出△ABC边AB上的高CD;
(2)在图2中,已知△ABC内部的点P也在格点上,点M,N分别在边AC,BC上,请画出周长最小的△PMN.
∴如图2,△PMN即为所求.
图1
A
C
B
D
∴如图1,线段CD即为所求.
图2
A
C
B
M
N
考点4-3
典例精讲
利用轴对称找最值
【例3-2】图1和图2均是由相同的小正方形组成的网格图,点A、B、C、D均落在格点上.请只用无刻度的直尺按下列要求画图.
(1)如图1,在格线CD上确定一点Q,使QA与QB的长度之和最小;
(2)如图2,在四边形ACBD的对角线CD上确定一点P,使∠APC=∠BPC.
利用将军饮马求相等的和的最值问题
Q
B
P
A
A
B
C
D
图1
A
C
B
D
图2
考点4-3
典例精讲
利用轴对称找最值
如图,在线段AB上找一点P,使AP:PB=3:2
A
B
考点4-4
理论依据
利用相似等分线段
P
P
A
B
P
P
利用“8(X)字形”相似作图
利用“A字形”相似作图
【例4-1】△ABC顶点均在网格的格点上,仅用无刻度的直尺作图.
(1)在图1中的线段AB上找一点D,连接CD,使S△ACD=S△ABC;
(2)在图2中的线段AB上找一点E,连接CE,使S△ACE=S△ABC;
图2
A
B
C
图1
A
B
C
D
E
∴△ACD即为所求
∴△ACE即为所求
考点4-4
典例精讲
利用相似等分线段
【例4-2】在正方形网格中,△ABC的三个顶点均在格点上,请仅用无刻度直尺,分别按下列要求画出线段EF.
(1)在图1中,点E,F分别在AB,AC上,EF∥BC且EF=BC;
(2)在图2中,点E,F分别在AB,AC上,EF∥BC且EF=BC.
A
C
B
图1
E
F
A
C
B
图2
E
F
∴EF即为所求
∴EF即为所求
考点4-4
典例精讲
利用相似等分线段
A
B
C
D
如图2
A
B
C
D
如图1
1.(2014·T17)已知梯形ABCD,请使用无刻度直尺画一个与梯形ABCD面积相等的图形.
(1)在图1中,画以CD为边的三角形;
(2)在图2中,画以AB为边的平行四边形.
E
F
E
如图1,△CDE即为所求;
如图2,□ABEF即为所求.
中考真题
配套训练
在网格线中作图
2.(2016·T17)如图,六个完全相同的小长方形拼成一个大长方形,AB是其中一个小长方形的对角线,请在大长方形中完成下列画图,要求:
1.仅用无刻度直尺;2.保留必要的画图痕迹.
(1)在图1中画一个45 角,使点A或点B是这个角的顶点,AB为这个角的一边.
(2)在图2中画出线段AB的垂直平分线.
图2
A
B
C
图1
A
B
如图1,∠BAC即为所求
如图2,EF即为所求
E
F
中考真题
配套训练
在网格线中作图
3.(2020·T16)如图,在正方形网格中,△ABC的顶点在格点上,请仅用无刻度直尺完成以下作图(保留作图痕迹).
(1)在图1中,作△ABC关于点O对称的△A B C ;
(2)在图2中,作△ABC绕点A顺时针旋转一定角度后,顶点仍在格点上的△A B C .
O
图1
A
C
B
图2
A
C
B
A
B
C
C
B
中考真题
配套训练
在网格线中作图
4.(2022 T16)如图是4×4的正方形网格,请仅用无刻度的直尺按要求完成以下作图(保留作图痕迹).
(1)在图1中作∠ABC的角平分线;
(2)在图2中过点C作一条直线l,使点A,B到直线l的距离相等.
C
A
B
图1
C
A
B
图2
D
∴BD即为所求
D
∴l即为所求
C
A
B
图2
D
l
l
∴l即为所求
中考真题
配套训练
在网格线中作图
5.(2023 T14)如图是4×4的正方形网格,请仅用无刻度的直尺按要求完成以下作图(保留作图痕迹).
(1)在图1中作锐角△ABC,使点C在格点上;
(2)在图2中的线段AB上作点Q,使PQ最短.
B
A
图1
B
A
图2
P
C1
C2
C3
C4
C5
C6
Q
∴△ABC即为所求
∴PQ即为所求
中考真题
配套训练
在网格线中作图
1.利用平移作平行线;
4.利用相似等分线段。
知识梳理
课堂小结
在网格线中作图
2.利用旋转作垂线;
3.利用轴对称找最值;
1.如图,在5×5的正方形网格中,△ABC顶点均为格点,请仅用无刻度直尺完成以下作图.
(1)在图1中,作出△ABC的高AM;
(2)在图2中,作出△ABC的高AN.
图1
C
B
A
图2
C
A
B
M
N
查漏补缺
配套训练
在网格线中作图
2.如图,在6×6的正方形网格中,△ABC的顶点在格点上,请仅用无刻度的直尺分别在图①、图②中画出△ABC的AB边上的高.
H
H
D
∴CH就是AB边上的高
∴CH就是AB边上的高
A
C
B
图1
A
B
C
图2
查漏补缺
配套训练
在网格线中作图
3.如图是4×4的网格,请仅用无刻度直尺完成以下作图.
(1)如图1,点A,B均在格点上,请过点A画出与AB垂直的直线AF;
(2)如图2,点A,B,C,D均在格点上,E是AC与BD的交点,请画出∠AEB的平分线EG.
A
B
图2
E
D
A
B
图1
G
C
∴EG即为所求
查漏补缺
配套训练
在网格线中作图
4.如图,在6×6的正方形网格中,等腰△ABC的顶点A,B在格点上,顶角∠A=36 ,请仅用无刻度直尺完成以下作图.
(1)在图1中,作△ABC的中线CD;
(2)在图2中,作△ABC的角平分线BE.
图1
A
C
B
图2
A
C
B
D
E
查漏补缺
配套训练
在网格线中作图
5.如图,在6×6的网格线中,四边形ABCD的顶点,点E都在格点上,仅用无刻度的直尺按下列要求作图.
(1)在图1中,作出△ABE关于直线l对称的△A1B1E1;
(2)如图2,在OC上找出点F,使EA平分∠BEF.
图1
A
E
B
O
l
图2
A
E
B
C
O
E1
(A1)
(B1)
F
△A1B1E1即为所求;
点F即为所求.
图2
A
E
B
C
O
F
点F即为所求.
查漏补缺
配套训练
在网格线中作图
6.利用网格和无刻度直尺按要求画图.
(1)如图1,在线段AB上找一点P,使AP=4BP;
(2)在图2中画出一条线段AB,使得AB=;
A
B
图1
P
图2
A
B
∴点P即为所求
∴AB即为所求
查漏补缺
配套训练
在网格线中作图
7.如图,在9×6的正方形网格中,点A,B,C均在格点(小正方形的顶点)上.请仅用无刻度的直尺按要求作图.
(1)在图1中,作格点D(不在直线BC上),使∠DBA=∠CBA;
(2)在图2中,E为AC上一点,在△ABC的内部作点P,使∠APB=∠APE.
∴如图2,点P即为所求.
图1
A
C
B
图2
A
E
C
B
D
∴如图1,点D即为所求.
P
查漏补缺
配套训练
在网格线中作图
8.如图,由6个形状,大小完全相同的小矩形组成大矩形网格,小矩形的顶点称为这个矩形网格的格点,请仅用无刻度直尺在矩形中完成下列画图.
(1)在图1中画出一个顶点均在格点上的非特殊的平行四边形;
(2)在图2中画出一个顶点均在格点上的非特殊的菱形.
图1
图2
D
A
B
C
A
B
C
D
如图1,四边形ABCD即为所求;
如图2,四边形ABCD即为所求.
查漏补缺
配套训练
在网格线中作图
提升能力
强化训练
在网格线中作图
A
B
1.如图,在由长为2,宽为1的矩形组成的网格中,已知A、B都是格点.请仅用无刻度的直尺在大长方形中完成下列作图.
(1)在图1中,画出线段AB的垂直平分线MN;
(2)在图2中,线段CD∥AB,画出线段CD的中点O.
A
B
C
D
O
N
M
利用梯形
四点共线作图
利用轴对称的性质作图
2.如图,射线OA放置在小正方形组成的网格中,现请你分别在图1,图2,图3中画射线OB,使tan∠AOB的值分别为1,,.
以OA为直角边
0
A
图1
B
B
B
0
A
图2
B
以OA为斜边
B
B
提升能力
强化训练
在网格线中作图
提升能力
强化训练
在网格线中作图
3.如图,是由小正方形组成的9×6网格,每个小正方形的顶点叫做格点.△ABC的顶点都是格点.仅用无刻度的直尺按下列要求作图.
(1)在图1中,D,E分别是边AB,AC与网格线的交点.在AC上画点G,使DG∥BC.
(2)在图2中,P是边AB上一点,∠BAC=α.先将AB绕点A逆时针旋转2α,得到线段AH,画出线段AH,再画点Q,使P,Q两点关于直线AC对称.
图1
A
D
C
B
图2
A
P
C
B
G
H
Q
4.如图,在边长为1个单位长度的小正方形组成的7×7的网格中,线段AB的端点为格点.仅用无刻度的直尺作图.
(1)在图1中,以线段AB为边作一个非正方形的菱形ABCD(点C,D也为格点)
(2)在图2中,以线段AB为底的等腰△PAB,(点P不一定为格点).
A
B
图1
A
B
图2
D
C
P
提升能力
强化训练
在网格线中作图
5.在6×6的正方形网格中,格点A,B在网格中的位置如图所示.请用无刻度直尺按要求画图.
(1)在图1中,画一个以A,B为顶点,另两个顶点也在格点上的正方形.
(2)在图2中,画一个以A,B为顶点,另两个顶点也在格点上的菱形,且使这个菱形的面积最小.
A
B
图1
A
B
图2
D
C
D
C
提升能力
强化训练
在网格线中作图
6.在下列6×6的正方形网格中,若每一个小正方形的边长均为1,请用无刻度直尺按要求画图:
(1)在图1中,以AB为边画一个正方形ABCD;
(2)在图2中,以AB为边画一个面积为5的矩形ABCD.
B
A
B
A
D
C
C
D
图1
图2
提升能力
强化训练
在网格线中作图
7.在10×10的正方形网格中,线段AB在网格中的位置如图所示,请用无刻度直尺按要求画图.
(1)在图1中,画菱形ABCD,且顶点C,D也在格点上;
(2)在图2中,画面积最大的菱形ABCD,且顶点C,D也在格点上.
与图形面积有关的作图
提升能力
强化训练
在网格线中作图
C
D
A
B
图1
A
B
图2
C
D
D
C
8.如图,在4×4的菱形网格图中(小菱形的边长为1,有一个角是60 ),请用无刻度直尺画顶点均落在格点上的面积最大的图形.
(1)在图1中画一个直角三角形;
(2)在图2中画一个四条边均不在网格线上的矩形.
图1
C
B
A
图2
A
C
D
B
提升能力
强化训练
在网格线中作图
A
B
C
图
2
A
B
C
图
1
9.如图,在8×6的正方形网格中,线段AB、BC的端点均在小正方形的顶点上,请仅用无刻度的直尺画图.
(1)在图1中找一点D(点D在小正方形的顶点上),连接AD、BD、CD,使△ABD与△BCD全等;
(2)在图2中找一点E(点E在格点上),使△ABE与△BCE均为以BE为直角边的直角三角形,且其中一个三角形的面积是另一个三角形面积的2倍.
与图形面积有关的作图
D
E
提升能力
强化训练
在网格线中作图
同课章节目录
