专题8.4创新作图---利用圆的定理作图 课件(共24张PPT)-中考数学二轮复习必会几何模型剖析(全国通用)
文档属性
| 名称 | 专题8.4创新作图---利用圆的定理作图 课件(共24张PPT)-中考数学二轮复习必会几何模型剖析(全国通用) |

|
|
| 格式 | pptx | ||
| 文件大小 | 5.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-25 00:00:00 | ||
图片预览






文档简介
(共24张PPT)
专题八 创新作图
人教版中考第二轮总复习---几何模型
8.4 利用圆的相关定理作图
是区别于尺规作图的另一种作图方式,它是以无刻度直尺作为唯一的作图工具,综合运用图形的几何性质、基本定理、图形变换等进行分析、推理、归纳,寻找作图依据。
考点归纳
题型概述
创新作图
创新作图:
创新作图的主要作图类型有:
1.在三角形中作图; 2.在特殊的四边形中作图;
3.在正多边形中作图; 4.在圆中作图; 5.在网格中作图。
无刻度直尺只能用来画直线,不能测量长度.
①找点:_________________________________________;
两条线相交的是点
两点确定一条直线
按要求构造三角形、四边形、正多边形等
(线可以是直线也可以是曲线)
考点归纳
题型概述
创新作图
创新作图的主要的作图要求有:
创新作图的常用的作图技巧有:
②画线:_________________________________________;
③构图:_________________________________________.
(确定圆心、弧的中点)
(作切线、直径、垂直平分线)
利用圆周角定理及其推论作图
01
利用切线判定定理作图
02
利用圆的性质在网格线中作图
03
知识要点
精讲精练
目录
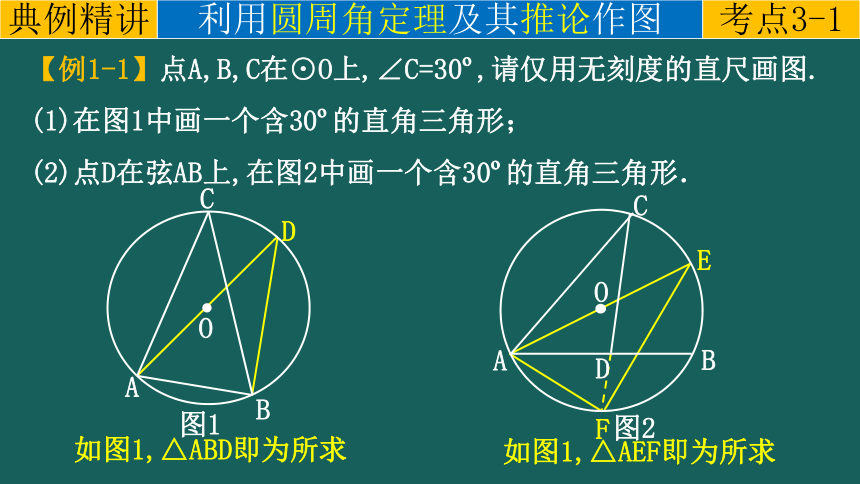
【例1-1】点A,B,C在⊙O上,∠C=30 ,请仅用无刻度的直尺画图.
(1)在图1中画一个含30 的直角三角形;
(2)点D在弦AB上,在图2中画一个含30 的直角三角形.
D
如图1,△ABD即为所求
F
E
如图1,△AEF即为所求
A
C
O
B
图1
A
C
O
B
图2
D
考点3-1
典例精讲
利用圆周角定理及其推论作图
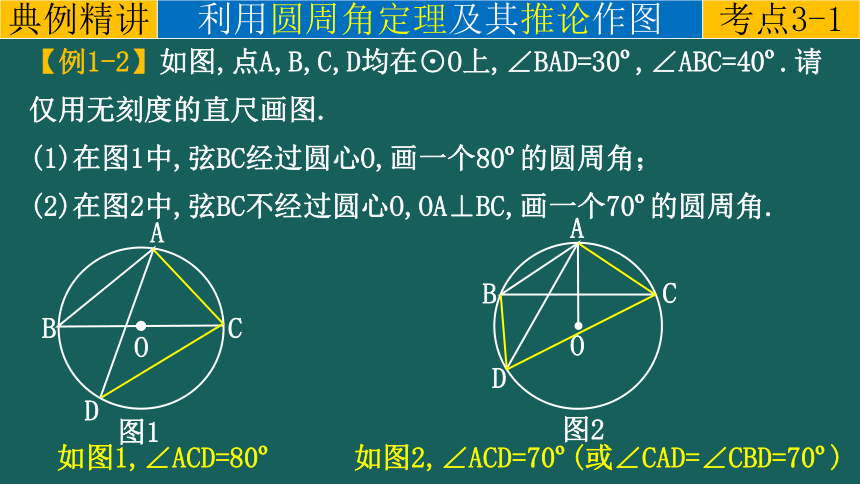
【例1-2】如图,点A,B,C,D均在⊙O上,∠BAD=30 ,∠ABC=40 .请仅用无刻度的直尺画图.
(1)在图1中,弦BC经过圆心O,画一个80 的圆周角;
(2)在图2中,弦BC不经过圆心O,OA⊥BC,画一个70 的圆周角.
B
A
O
C
图1
D
B
A
O
C
图2
D
如图1,∠ACD=80
如图2,∠ACD=70 (或∠CAD=∠CBD=70 )
考点3-1
典例精讲
利用圆周角定理及其推论作图
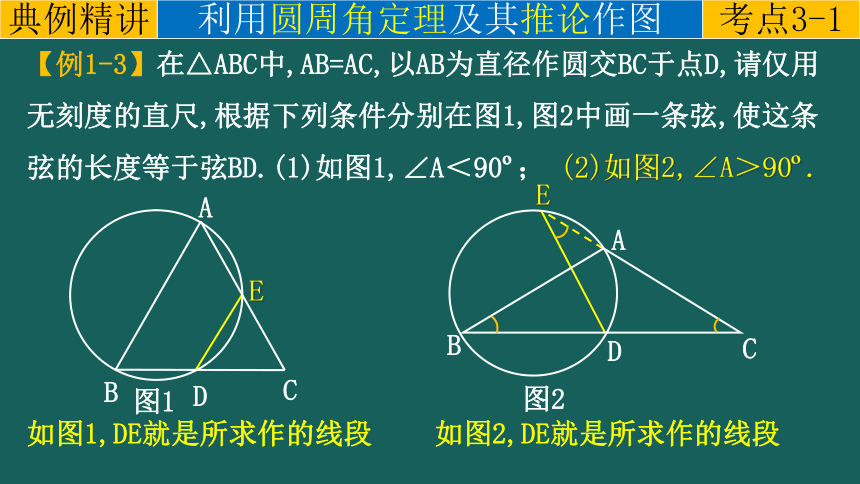
【例1-3】在△ABC中,AB=AC,以AB为直径作圆交BC于点D,请仅用无刻度的直尺,根据下列条件分别在图1,图2中画一条弦,使这条弦的长度等于弦BD.(1)如图1,∠A<90 ; (2)如图2,∠A>90 .
E
A
C
D
B
图1
E
A
D
C
B
图2
如图1,DE就是所求作的线段
如图2,DE就是所求作的线段
考点3-1
典例精讲
利用圆周角定理及其推论作图
利用圆周角定理及其推论作图
01
利用切线判定定理作图
02
利用圆的性质在网格线中作图
03
知识要点
精讲精练
目录
【例2-1】如图,AB是⊙O的直径,AC是⊙O的切线,AC=AB,请仅用无刻度的直尺画图.(1)在图1中,画出△ABC的中线BE;
(2)在图2中,画出以D为切点⊙O的切线DT.
E
T
图2
B
A
C
D
O
图1
B
A
C
D
O
如图1,线段BE即为所求
如图2,线段DT即为所求
考点3-2
典例精讲
利用切线判定定理作图
【例2-2】如图,四边形ABCD为菱形,以AD为直径作⊙O,请仅用无刻度的直尺按要求画图.
(1)如图1,当∠ADC=60 时,⊙O与DC相交于点M,过M作⊙O的切线
(2)如图2,当∠ADC=90 时,过点C作⊙O的切线(CD除外)
A
O
B
图1
C
D
M
N
图2
O
D
C
B
A
E
考点3-2
典例精讲
利用切线判定定理作图
利用圆周角定理及其推论作图
01
利用切线判定定理作图
02
利用圆的性质在网格线中作图
03
知识要点
精讲精练
目录
【例3】如图,在8×8的网格纸中,点O和点A都是格点,以O为圆心,OA为半径作圆.请仅用无刻度直尺作图.
(1)在图1中画⊙O的一个内接正八边形ABCDEFGH;
(2)在图2中画⊙O的一个内接正六边形ABCDEF;
图1
O
A
图2
O
A
H
G
F
E
D
C
B
B
C
D
E
F
考点4-3
典例精讲
构图---正多边形
∴正八边形ABCDEFGH即为所求
∴正六边形ABCDEF即为所求
2.(2015·T17)⊙O为△ABC的外接圆,请仅用无刻度的直尺,根据下列条件分别在图1,图2中画出一条弦,使这条弦将△ABC分成面积相等的两部分. (1)如图1,AC=BC; (2)如图2,直线l与⊙O相切与点P,且l∥BC.
O
B
C
A
图1
O
B
C
A
图2
P
l
D
D
如图1,CD即为所求
如图2,AD即为所求
中考真题
配套训练
利用性质作位置、数量关系
3.(2019·T15)在△ABC中,AB=AC,点A在以BC为直径的半圆内.请仅用无刻度的直尺分别按下列要求画图.
(1)在图1中作弦EF,使EF∥BC;
(2)在图2中以BC为边作一个45 的圆周角.
A
C
B
图1
A
C
B
图2
F
E
P
如图2,∠PBC=45
如图1,EF即为所求
中考真题
配套训练
利用性质作位置、数量关系
知识梳理
课堂小结
利用圆的相关定理作图
1.利用圆周角定理及其推论作图
2.利用切线判定定理作图
3.利用圆的性质在网格线中作图
1.如图,已知△ABC内接于⊙O,且∠B=75 ,∠C=45 ,⊙O的半径为R.请仅用无刻度的直尺作图.
(1)在图1中,画出一条长度为R的弦;
(2)在图2中,画出一个内接于⊙O的正方形.
B
C
A
O
图1
B
C
A
O
图2
D
D
E
如图2,正方形ABED即为所求.
如图1,弦CD为所求作的弦;
提升能力
强化训练
利用圆的相关定理作图
2.如图,已知四边形ABCD内接于⊙O,且已知∠ADC=120 ;请仅用无刻度的直尺完成以下作图.
(1)在图1中,已知AD=CD,在⊙O上求作一个度数为30 的圆周角;
(2)在图2中,已知AD≠CD,在⊙O上求作一个度数为30 的圆周角.
如图1,∠ABD(∠CBD)即为所求
B
图1
D
C
A
O
如图2,∠CAE即为所求
B
图2
D
C
A
O
E
B
图2
D
C
A
O
E
提升能力
强化训练
利用圆的相关定理作图
3.如图,圆与等边△ABC的边BC相切于点B,且圆过AB的中点M,请仅用无刻度直尺,分别按下列要求作图.
(1)在图(1)中,作圆的直径;
(2)在图(2)中,作以AB为腰且腰与底边不相等的等腰三角形.
D
如图(1),BD就是圆的直径
A
M
C
B
图1
如图(2),△ABE就是所求作的三角形
E
E
A
M
C
B
图2
提升能力
强化训练
利用圆的相关定理作图
4.如图,在由边长均为1的正方形构成的网格中有一个圆心为O的半圆(点O在格点上,且半径为2),请利用无刻度的直尺完成作图.
(1)在图1中画出一个45 且顶点在格点上的圆周角;
(2)在图2中画出一个22.5 且顶点在格点上的圆周角.
B
C
A
C
B
A
O
图1
O
图2
∴∠CAB即为所求;
∴∠CAB即为所求;
提升能力
强化训练
利用圆的相关定理作图
5.如图,⊙P经过A,B,C三个格点,请仅用无刻度直尺作图,
(1)画出圆心P;
(2)画弦BD平分∠ABC.
C
A
B
图1
C
A
B
图2
P
D
∴点P即为所求;
∴弦BD即为所求;
提升能力
强化训练
利用圆的相关定理作图
6.如图,在边长为1的正方形网格中有一段圆弧AC,弧AC经过格点A,B,C,请仅用无刻度的直尺分别按下列要求画图.
(1)在图①中,画出弧AC所在圆的圆心O;
(2)在图②中,画出弧AC所在圆的一条切线,使这条切线经过格点P.
图1
A
C
B
图2
A
B
C
P
提升能力
强化训练
利用圆的相关定理作图
7.如图,已知AB是⊙O的直径,在四边形ABCD中,BC=CD=DA,且CD∥AB,请仅用无刻度的直尺按下列要求画图.
(1)在图1中作∠BCD的平分线;
(2)在图2中在圆上任选两点M,N(不与A,B,C,D重合),使MN=BC.
M
N
B
图1
D
C
A
O
B
图2
D
C
A
O
∴如图1,CO就是∠BCD的平分线
∴如图2,MN就是所求作的线段
提升能力
强化训练
利用圆的相关定理作图
8.如图,A、B在圆上,图1中,点P在圆内,图2中,点P在圆外,请仅用无刻度的直尺按要求画图.求作△CDP,使△CDP与△ABP相似,且C、D在圆上,相似比不为1.
C
D
A
P
B
O
图1
C
D
A
P
B
O
图2
提升能力
强化训练
利用圆的相关定理作图
9.已知的面积为10,请请用无刻度的直尺作一个三角形,使所求作的三角形的面积等于5.
(1)如图1,在△ABC中,点D在BC上,以AD为直径作半圆O,半圆O经过点C.
(2)如图2,在△ABC中,DE∥BF,EF∥AB.
A
图1
B
O
C
D
A
E
D
F
C
B
图2
O
如图1,△BOC的面积为5.
如图2,△AOC的面积为5.
提升能力
强化训练
利用圆的相关定理作图
专题八 创新作图
人教版中考第二轮总复习---几何模型
8.4 利用圆的相关定理作图
是区别于尺规作图的另一种作图方式,它是以无刻度直尺作为唯一的作图工具,综合运用图形的几何性质、基本定理、图形变换等进行分析、推理、归纳,寻找作图依据。
考点归纳
题型概述
创新作图
创新作图:
创新作图的主要作图类型有:
1.在三角形中作图; 2.在特殊的四边形中作图;
3.在正多边形中作图; 4.在圆中作图; 5.在网格中作图。
无刻度直尺只能用来画直线,不能测量长度.
①找点:_________________________________________;
两条线相交的是点
两点确定一条直线
按要求构造三角形、四边形、正多边形等
(线可以是直线也可以是曲线)
考点归纳
题型概述
创新作图
创新作图的主要的作图要求有:
创新作图的常用的作图技巧有:
②画线:_________________________________________;
③构图:_________________________________________.
(确定圆心、弧的中点)
(作切线、直径、垂直平分线)
利用圆周角定理及其推论作图
01
利用切线判定定理作图
02
利用圆的性质在网格线中作图
03
知识要点
精讲精练
目录
【例1-1】点A,B,C在⊙O上,∠C=30 ,请仅用无刻度的直尺画图.
(1)在图1中画一个含30 的直角三角形;
(2)点D在弦AB上,在图2中画一个含30 的直角三角形.
D
如图1,△ABD即为所求
F
E
如图1,△AEF即为所求
A
C
O
B
图1
A
C
O
B
图2
D
考点3-1
典例精讲
利用圆周角定理及其推论作图
【例1-2】如图,点A,B,C,D均在⊙O上,∠BAD=30 ,∠ABC=40 .请仅用无刻度的直尺画图.
(1)在图1中,弦BC经过圆心O,画一个80 的圆周角;
(2)在图2中,弦BC不经过圆心O,OA⊥BC,画一个70 的圆周角.
B
A
O
C
图1
D
B
A
O
C
图2
D
如图1,∠ACD=80
如图2,∠ACD=70 (或∠CAD=∠CBD=70 )
考点3-1
典例精讲
利用圆周角定理及其推论作图
【例1-3】在△ABC中,AB=AC,以AB为直径作圆交BC于点D,请仅用无刻度的直尺,根据下列条件分别在图1,图2中画一条弦,使这条弦的长度等于弦BD.(1)如图1,∠A<90 ; (2)如图2,∠A>90 .
E
A
C
D
B
图1
E
A
D
C
B
图2
如图1,DE就是所求作的线段
如图2,DE就是所求作的线段
考点3-1
典例精讲
利用圆周角定理及其推论作图
利用圆周角定理及其推论作图
01
利用切线判定定理作图
02
利用圆的性质在网格线中作图
03
知识要点
精讲精练
目录
【例2-1】如图,AB是⊙O的直径,AC是⊙O的切线,AC=AB,请仅用无刻度的直尺画图.(1)在图1中,画出△ABC的中线BE;
(2)在图2中,画出以D为切点⊙O的切线DT.
E
T
图2
B
A
C
D
O
图1
B
A
C
D
O
如图1,线段BE即为所求
如图2,线段DT即为所求
考点3-2
典例精讲
利用切线判定定理作图
【例2-2】如图,四边形ABCD为菱形,以AD为直径作⊙O,请仅用无刻度的直尺按要求画图.
(1)如图1,当∠ADC=60 时,⊙O与DC相交于点M,过M作⊙O的切线
(2)如图2,当∠ADC=90 时,过点C作⊙O的切线(CD除外)
A
O
B
图1
C
D
M
N
图2
O
D
C
B
A
E
考点3-2
典例精讲
利用切线判定定理作图
利用圆周角定理及其推论作图
01
利用切线判定定理作图
02
利用圆的性质在网格线中作图
03
知识要点
精讲精练
目录
【例3】如图,在8×8的网格纸中,点O和点A都是格点,以O为圆心,OA为半径作圆.请仅用无刻度直尺作图.
(1)在图1中画⊙O的一个内接正八边形ABCDEFGH;
(2)在图2中画⊙O的一个内接正六边形ABCDEF;
图1
O
A
图2
O
A
H
G
F
E
D
C
B
B
C
D
E
F
考点4-3
典例精讲
构图---正多边形
∴正八边形ABCDEFGH即为所求
∴正六边形ABCDEF即为所求
2.(2015·T17)⊙O为△ABC的外接圆,请仅用无刻度的直尺,根据下列条件分别在图1,图2中画出一条弦,使这条弦将△ABC分成面积相等的两部分. (1)如图1,AC=BC; (2)如图2,直线l与⊙O相切与点P,且l∥BC.
O
B
C
A
图1
O
B
C
A
图2
P
l
D
D
如图1,CD即为所求
如图2,AD即为所求
中考真题
配套训练
利用性质作位置、数量关系
3.(2019·T15)在△ABC中,AB=AC,点A在以BC为直径的半圆内.请仅用无刻度的直尺分别按下列要求画图.
(1)在图1中作弦EF,使EF∥BC;
(2)在图2中以BC为边作一个45 的圆周角.
A
C
B
图1
A
C
B
图2
F
E
P
如图2,∠PBC=45
如图1,EF即为所求
中考真题
配套训练
利用性质作位置、数量关系
知识梳理
课堂小结
利用圆的相关定理作图
1.利用圆周角定理及其推论作图
2.利用切线判定定理作图
3.利用圆的性质在网格线中作图
1.如图,已知△ABC内接于⊙O,且∠B=75 ,∠C=45 ,⊙O的半径为R.请仅用无刻度的直尺作图.
(1)在图1中,画出一条长度为R的弦;
(2)在图2中,画出一个内接于⊙O的正方形.
B
C
A
O
图1
B
C
A
O
图2
D
D
E
如图2,正方形ABED即为所求.
如图1,弦CD为所求作的弦;
提升能力
强化训练
利用圆的相关定理作图
2.如图,已知四边形ABCD内接于⊙O,且已知∠ADC=120 ;请仅用无刻度的直尺完成以下作图.
(1)在图1中,已知AD=CD,在⊙O上求作一个度数为30 的圆周角;
(2)在图2中,已知AD≠CD,在⊙O上求作一个度数为30 的圆周角.
如图1,∠ABD(∠CBD)即为所求
B
图1
D
C
A
O
如图2,∠CAE即为所求
B
图2
D
C
A
O
E
B
图2
D
C
A
O
E
提升能力
强化训练
利用圆的相关定理作图
3.如图,圆与等边△ABC的边BC相切于点B,且圆过AB的中点M,请仅用无刻度直尺,分别按下列要求作图.
(1)在图(1)中,作圆的直径;
(2)在图(2)中,作以AB为腰且腰与底边不相等的等腰三角形.
D
如图(1),BD就是圆的直径
A
M
C
B
图1
如图(2),△ABE就是所求作的三角形
E
E
A
M
C
B
图2
提升能力
强化训练
利用圆的相关定理作图
4.如图,在由边长均为1的正方形构成的网格中有一个圆心为O的半圆(点O在格点上,且半径为2),请利用无刻度的直尺完成作图.
(1)在图1中画出一个45 且顶点在格点上的圆周角;
(2)在图2中画出一个22.5 且顶点在格点上的圆周角.
B
C
A
C
B
A
O
图1
O
图2
∴∠CAB即为所求;
∴∠CAB即为所求;
提升能力
强化训练
利用圆的相关定理作图
5.如图,⊙P经过A,B,C三个格点,请仅用无刻度直尺作图,
(1)画出圆心P;
(2)画弦BD平分∠ABC.
C
A
B
图1
C
A
B
图2
P
D
∴点P即为所求;
∴弦BD即为所求;
提升能力
强化训练
利用圆的相关定理作图
6.如图,在边长为1的正方形网格中有一段圆弧AC,弧AC经过格点A,B,C,请仅用无刻度的直尺分别按下列要求画图.
(1)在图①中,画出弧AC所在圆的圆心O;
(2)在图②中,画出弧AC所在圆的一条切线,使这条切线经过格点P.
图1
A
C
B
图2
A
B
C
P
提升能力
强化训练
利用圆的相关定理作图
7.如图,已知AB是⊙O的直径,在四边形ABCD中,BC=CD=DA,且CD∥AB,请仅用无刻度的直尺按下列要求画图.
(1)在图1中作∠BCD的平分线;
(2)在图2中在圆上任选两点M,N(不与A,B,C,D重合),使MN=BC.
M
N
B
图1
D
C
A
O
B
图2
D
C
A
O
∴如图1,CO就是∠BCD的平分线
∴如图2,MN就是所求作的线段
提升能力
强化训练
利用圆的相关定理作图
8.如图,A、B在圆上,图1中,点P在圆内,图2中,点P在圆外,请仅用无刻度的直尺按要求画图.求作△CDP,使△CDP与△ABP相似,且C、D在圆上,相似比不为1.
C
D
A
P
B
O
图1
C
D
A
P
B
O
图2
提升能力
强化训练
利用圆的相关定理作图
9.已知的面积为10,请请用无刻度的直尺作一个三角形,使所求作的三角形的面积等于5.
(1)如图1,在△ABC中,点D在BC上,以AD为直径作半圆O,半圆O经过点C.
(2)如图2,在△ABC中,DE∥BF,EF∥AB.
A
图1
B
O
C
D
A
E
D
F
C
B
图2
O
如图1,△BOC的面积为5.
如图2,△AOC的面积为5.
提升能力
强化训练
利用圆的相关定理作图
同课章节目录
