浙江省中考数学考前冲刺每日一练21(精选全省各市历年经典真题,包含常考题型、易错题型、 小压轴、大压轴)
文档属性
| 名称 | 浙江省中考数学考前冲刺每日一练21(精选全省各市历年经典真题,包含常考题型、易错题型、 小压轴、大压轴) |

|
|
| 格式 | doc | ||
| 文件大小 | 375.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-24 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
浙江省中考数学考前冲刺每日一练21(精选全省各市历年经典真题,包含常考题型、易错题型、 小压轴、大压轴)
1.地球上煤的储量估计为15万亿吨以上,15万亿吨用科学记数法表示为( )
A.1.5×1011吨 B.1.5×1012吨 C.1.5×1013吨 D.1.5×1014吨
2.如图,△ABC内接于⊙O,EF为⊙O直径,点F是BC弧的中点,若∠B=40°,∠C=60°,则∠AFE的度数( )
A.10° B.20° C.30° D.40°
3.将抛物线y=ax2+bx+c向左平移2个单位,再向下平移5个单位,得到抛物线y=x2+4x﹣1,则a+b+c= .
4.如图,在 ABCD中,AF、BE分别平分∠DAB、∠ABC,点G是AF、BE的交点,AB=5,BC=3,则S△EFG:S△ABG= .
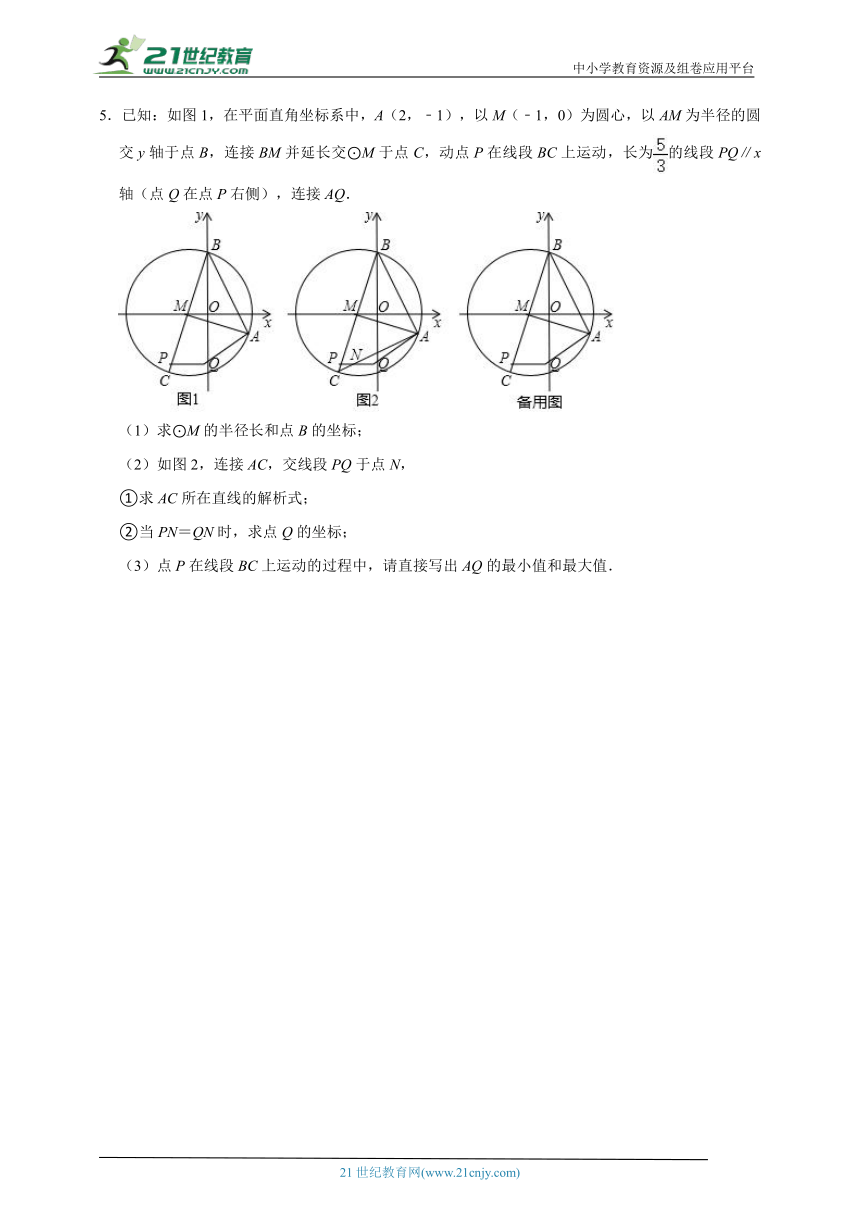
5.已知:如图1,在平面直角坐标系中,A(2,﹣1),以M(﹣1,0)为圆心,以AM为半径的圆交y轴于点B,连接BM并延长交⊙M于点C,动点P在线段BC上运动,长为的线段PQ∥x轴(点Q在点P右侧),连接AQ.
(1)求⊙M的半径长和点B的坐标;
(2)如图2,连接AC,交线段PQ于点N,
①求AC所在直线的解析式;
②当PN=QN时,求点Q的坐标;
(3)点P在线段BC上运动的过程中,请直接写出AQ的最小值和最大值.
浙江省中考数学考前冲刺每日一练21(精选全省各市历年经典真题,包含常考题型、易错题型、 小压轴、大压轴)参考答案与试题解析
一.选择题(共2小题)
1.地球上煤的储量估计为15万亿吨以上,15万亿吨用科学记数法表示为( )
A.1.5×1011吨 B.1.5×1012吨 C.1.5×1013吨 D.1.5×1014吨
【分析】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值≥10时,n是正整数,当原数绝对值<1时,n是负整数.
【解答】解:15万亿=150000亿=15000000000000=1.5×1013.
故选:C.
【点评】此题考查科学记数法的表示方法.科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数,表示时关键要正确确定a的值以及n的值.
2.如图,△ABC内接于⊙O,EF为⊙O直径,点F是BC弧的中点,若∠B=40°,∠C=60°,则∠AFE的度数( )
A.10° B.20° C.30° D.40°
【分析】连接AE,根据圆周角定理即可得到结论.
【解答】解:连接AE,
∵EF为⊙O直径,
∴∠EAF=90°,
∵点F是BC弧的中点,
∴=,
∵∠B=40°,∠C=60°,
∴∠BAC=80°,
∴∠BAF=∠CAF=40°,
∴∠E=∠B+∠FAC=80°,
∴∠AFE=90°﹣80°=10°,
故选:A.
【点评】本题考查了三角形的外接圆与外心,圆周角定理,正确的识别图形是解题的关键.
二.填空题(共2小题)
3.将抛物线y=ax2+bx+c向左平移2个单位,再向下平移5个单位,得到抛物线y=x2+4x﹣1,则a+b+c= 1 .
【分析】抛物线平移.不改变二次项系数,平移后抛物线的顶点坐标为(﹣2,﹣5),根据平移规律可推出原抛物线顶点坐标为(0,0),根据顶点式可求抛物线解析式.
【解答】解:平移后的抛物线y=x2+4x﹣1=(x+2)2﹣5,顶点为(﹣2,﹣5),
根据平移规律,得原抛物线顶点坐标为(0,0),
又平移不改变二次项系数,
∴原抛物线解析式为y=x2,
∴a=1,b=c=0,
∴a+b+c=1,
故答案为1.
【点评】本题主要考查了函数图象的平移,抛物线与坐标轴的交点坐标的求法,要求熟练掌握平移的规律:左加右减,上加下减.并用规律求函数解析式.
4.如图,在 ABCD中,AF、BE分别平分∠DAB、∠ABC,点G是AF、BE的交点,AB=5,BC=3,则S△EFG:S△ABG= 1:25 .
【分析】要证S△EFG:S△ABG,只要证明△EFG∽△ABG,则有,即可求解.
【解答】解:
∵BE分别平分ABC
∴∠ABE=∠EBC
∵在 ABCD中,DC∥AB
∴∠ABE=∠EBC=∠BEC
∴CE=BC=3
同理可得∠DAF=∠DFA,AD=DF=3
∵在 ABCD中,AB=DC=5
∴EF=1
∵在△EFG和△ABG中,
∴△EFG∽△ABG
∴==
故答案为:1:25
【点评】此题主要考查平行四边形的两组对边分别相等,有两组角对应相等的两个三角形相似,两底角相等的三角形为等腰三角形.
三.解答题(共1小题)
5.已知:如图1,在平面直角坐标系中,A(2,﹣1),以M(﹣1,0)为圆心,以AM为半径的圆交y轴于点B,连接BM并延长交⊙M于点C,动点P在线段BC上运动,长为的线段PQ∥x轴(点Q在点P右侧),连接AQ.
(1)求⊙M的半径长和点B的坐标;
(2)如图2,连接AC,交线段PQ于点N,
①求AC所在直线的解析式;
②当PN=QN时,求点Q的坐标;
(3)点P在线段BC上运动的过程中,请直接写出AQ的最小值和最大值.
【分析】(1)如图1中,过点A作AE⊥x轴,分别在Rt△AEM和Rt△NOM中利用勾股定理即可解决问题.
(2)①设解析式为设yAC=kx+b,利用待定系数法即可解决问题.②可求yBC=3x+3,设点P(x,3x+3).由题意得点N为(x+,3x+3),因为点N落在AC上,所以3x+3=( x+)﹣2,列方程即可解决问题.
(3)当点P与C重合时,Q(﹣,﹣3),此时AQ′=,过点Q平行BC的直线的解析式为y=3x﹣2,过点A垂直BC的直线的解析式为y=﹣x﹣,与直线y=3x﹣2的交点为Q′,此时AQ′最小,当点P与点B重合时,Q″(,3),此时AQ″==,由此即可判断PQ的最大值.
【解答】解:(1)如图1中,过点A作AE⊥x轴,
则AE=1,ME=3,
∴AM==,即半径为,
所以BM=,
∵OM=1,
∴OB==3,即点B(0,3).
(2)如图2中,
①设解析式为设yAC=kx+b,
由题意得点C与点B关于点M成中心对称,
∴点C(﹣2,﹣3)(也可以通过构造全等三角形说明),
又点A(2,﹣1),
即当x=2时,y=﹣1;当x=﹣2时,y=﹣3,
解得k=,b=﹣2
∴yAC=x﹣2,
②可求yBC=3x+3,设点P(x,3x+3).
由题意得点N为(x+,3x+3)
∵点N落在AC上,所以3x+3=( x+)﹣2
解得x=﹣
所以点Q坐标为(﹣,﹣).
(3)如图3中,
当点P与C重合时,Q(﹣,﹣3),此时AQ′=,过点Q平行BC的直线的解析式为y=3x﹣2,
过点A垂直BC的直线的解析式为y=﹣x﹣,与直线y=3x﹣2的交点为Q′,此时AQ′最小(垂线段最短),
由,解得,
∴Q′(,﹣),
∴AQ的最小值为=.
当点P与点B重合时,Q″(,3),此时AQ″==,
∴AQ最大值为.
【点评】本题考查圆综合题、一次函数的应用、勾股定理、待定系数法、垂线段最短等知识,解题的关键是灵活运用所学知识解决问题,学会构建一次函数,利用方程组求两个函数的交点坐标,属于中考压轴题.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
浙江省中考数学考前冲刺每日一练21(精选全省各市历年经典真题,包含常考题型、易错题型、 小压轴、大压轴)
1.地球上煤的储量估计为15万亿吨以上,15万亿吨用科学记数法表示为( )
A.1.5×1011吨 B.1.5×1012吨 C.1.5×1013吨 D.1.5×1014吨
2.如图,△ABC内接于⊙O,EF为⊙O直径,点F是BC弧的中点,若∠B=40°,∠C=60°,则∠AFE的度数( )
A.10° B.20° C.30° D.40°
3.将抛物线y=ax2+bx+c向左平移2个单位,再向下平移5个单位,得到抛物线y=x2+4x﹣1,则a+b+c= .
4.如图,在 ABCD中,AF、BE分别平分∠DAB、∠ABC,点G是AF、BE的交点,AB=5,BC=3,则S△EFG:S△ABG= .
5.已知:如图1,在平面直角坐标系中,A(2,﹣1),以M(﹣1,0)为圆心,以AM为半径的圆交y轴于点B,连接BM并延长交⊙M于点C,动点P在线段BC上运动,长为的线段PQ∥x轴(点Q在点P右侧),连接AQ.
(1)求⊙M的半径长和点B的坐标;
(2)如图2,连接AC,交线段PQ于点N,
①求AC所在直线的解析式;
②当PN=QN时,求点Q的坐标;
(3)点P在线段BC上运动的过程中,请直接写出AQ的最小值和最大值.
浙江省中考数学考前冲刺每日一练21(精选全省各市历年经典真题,包含常考题型、易错题型、 小压轴、大压轴)参考答案与试题解析
一.选择题(共2小题)
1.地球上煤的储量估计为15万亿吨以上,15万亿吨用科学记数法表示为( )
A.1.5×1011吨 B.1.5×1012吨 C.1.5×1013吨 D.1.5×1014吨
【分析】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值≥10时,n是正整数,当原数绝对值<1时,n是负整数.
【解答】解:15万亿=150000亿=15000000000000=1.5×1013.
故选:C.
【点评】此题考查科学记数法的表示方法.科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数,表示时关键要正确确定a的值以及n的值.
2.如图,△ABC内接于⊙O,EF为⊙O直径,点F是BC弧的中点,若∠B=40°,∠C=60°,则∠AFE的度数( )
A.10° B.20° C.30° D.40°
【分析】连接AE,根据圆周角定理即可得到结论.
【解答】解:连接AE,
∵EF为⊙O直径,
∴∠EAF=90°,
∵点F是BC弧的中点,
∴=,
∵∠B=40°,∠C=60°,
∴∠BAC=80°,
∴∠BAF=∠CAF=40°,
∴∠E=∠B+∠FAC=80°,
∴∠AFE=90°﹣80°=10°,
故选:A.
【点评】本题考查了三角形的外接圆与外心,圆周角定理,正确的识别图形是解题的关键.
二.填空题(共2小题)
3.将抛物线y=ax2+bx+c向左平移2个单位,再向下平移5个单位,得到抛物线y=x2+4x﹣1,则a+b+c= 1 .
【分析】抛物线平移.不改变二次项系数,平移后抛物线的顶点坐标为(﹣2,﹣5),根据平移规律可推出原抛物线顶点坐标为(0,0),根据顶点式可求抛物线解析式.
【解答】解:平移后的抛物线y=x2+4x﹣1=(x+2)2﹣5,顶点为(﹣2,﹣5),
根据平移规律,得原抛物线顶点坐标为(0,0),
又平移不改变二次项系数,
∴原抛物线解析式为y=x2,
∴a=1,b=c=0,
∴a+b+c=1,
故答案为1.
【点评】本题主要考查了函数图象的平移,抛物线与坐标轴的交点坐标的求法,要求熟练掌握平移的规律:左加右减,上加下减.并用规律求函数解析式.
4.如图,在 ABCD中,AF、BE分别平分∠DAB、∠ABC,点G是AF、BE的交点,AB=5,BC=3,则S△EFG:S△ABG= 1:25 .
【分析】要证S△EFG:S△ABG,只要证明△EFG∽△ABG,则有,即可求解.
【解答】解:
∵BE分别平分ABC
∴∠ABE=∠EBC
∵在 ABCD中,DC∥AB
∴∠ABE=∠EBC=∠BEC
∴CE=BC=3
同理可得∠DAF=∠DFA,AD=DF=3
∵在 ABCD中,AB=DC=5
∴EF=1
∵在△EFG和△ABG中,
∴△EFG∽△ABG
∴==
故答案为:1:25
【点评】此题主要考查平行四边形的两组对边分别相等,有两组角对应相等的两个三角形相似,两底角相等的三角形为等腰三角形.
三.解答题(共1小题)
5.已知:如图1,在平面直角坐标系中,A(2,﹣1),以M(﹣1,0)为圆心,以AM为半径的圆交y轴于点B,连接BM并延长交⊙M于点C,动点P在线段BC上运动,长为的线段PQ∥x轴(点Q在点P右侧),连接AQ.
(1)求⊙M的半径长和点B的坐标;
(2)如图2,连接AC,交线段PQ于点N,
①求AC所在直线的解析式;
②当PN=QN时,求点Q的坐标;
(3)点P在线段BC上运动的过程中,请直接写出AQ的最小值和最大值.
【分析】(1)如图1中,过点A作AE⊥x轴,分别在Rt△AEM和Rt△NOM中利用勾股定理即可解决问题.
(2)①设解析式为设yAC=kx+b,利用待定系数法即可解决问题.②可求yBC=3x+3,设点P(x,3x+3).由题意得点N为(x+,3x+3),因为点N落在AC上,所以3x+3=( x+)﹣2,列方程即可解决问题.
(3)当点P与C重合时,Q(﹣,﹣3),此时AQ′=,过点Q平行BC的直线的解析式为y=3x﹣2,过点A垂直BC的直线的解析式为y=﹣x﹣,与直线y=3x﹣2的交点为Q′,此时AQ′最小,当点P与点B重合时,Q″(,3),此时AQ″==,由此即可判断PQ的最大值.
【解答】解:(1)如图1中,过点A作AE⊥x轴,
则AE=1,ME=3,
∴AM==,即半径为,
所以BM=,
∵OM=1,
∴OB==3,即点B(0,3).
(2)如图2中,
①设解析式为设yAC=kx+b,
由题意得点C与点B关于点M成中心对称,
∴点C(﹣2,﹣3)(也可以通过构造全等三角形说明),
又点A(2,﹣1),
即当x=2时,y=﹣1;当x=﹣2时,y=﹣3,
解得k=,b=﹣2
∴yAC=x﹣2,
②可求yBC=3x+3,设点P(x,3x+3).
由题意得点N为(x+,3x+3)
∵点N落在AC上,所以3x+3=( x+)﹣2
解得x=﹣
所以点Q坐标为(﹣,﹣).
(3)如图3中,
当点P与C重合时,Q(﹣,﹣3),此时AQ′=,过点Q平行BC的直线的解析式为y=3x﹣2,
过点A垂直BC的直线的解析式为y=﹣x﹣,与直线y=3x﹣2的交点为Q′,此时AQ′最小(垂线段最短),
由,解得,
∴Q′(,﹣),
∴AQ的最小值为=.
当点P与点B重合时,Q″(,3),此时AQ″==,
∴AQ最大值为.
【点评】本题考查圆综合题、一次函数的应用、勾股定理、待定系数法、垂线段最短等知识,解题的关键是灵活运用所学知识解决问题,学会构建一次函数,利用方程组求两个函数的交点坐标,属于中考压轴题.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
