浙江省中考数学考前冲刺每日一练25(精选全省各市历年经典真题,包含常考题型、易错题型、 小压轴、大压轴)
文档属性
| 名称 | 浙江省中考数学考前冲刺每日一练25(精选全省各市历年经典真题,包含常考题型、易错题型、 小压轴、大压轴) | 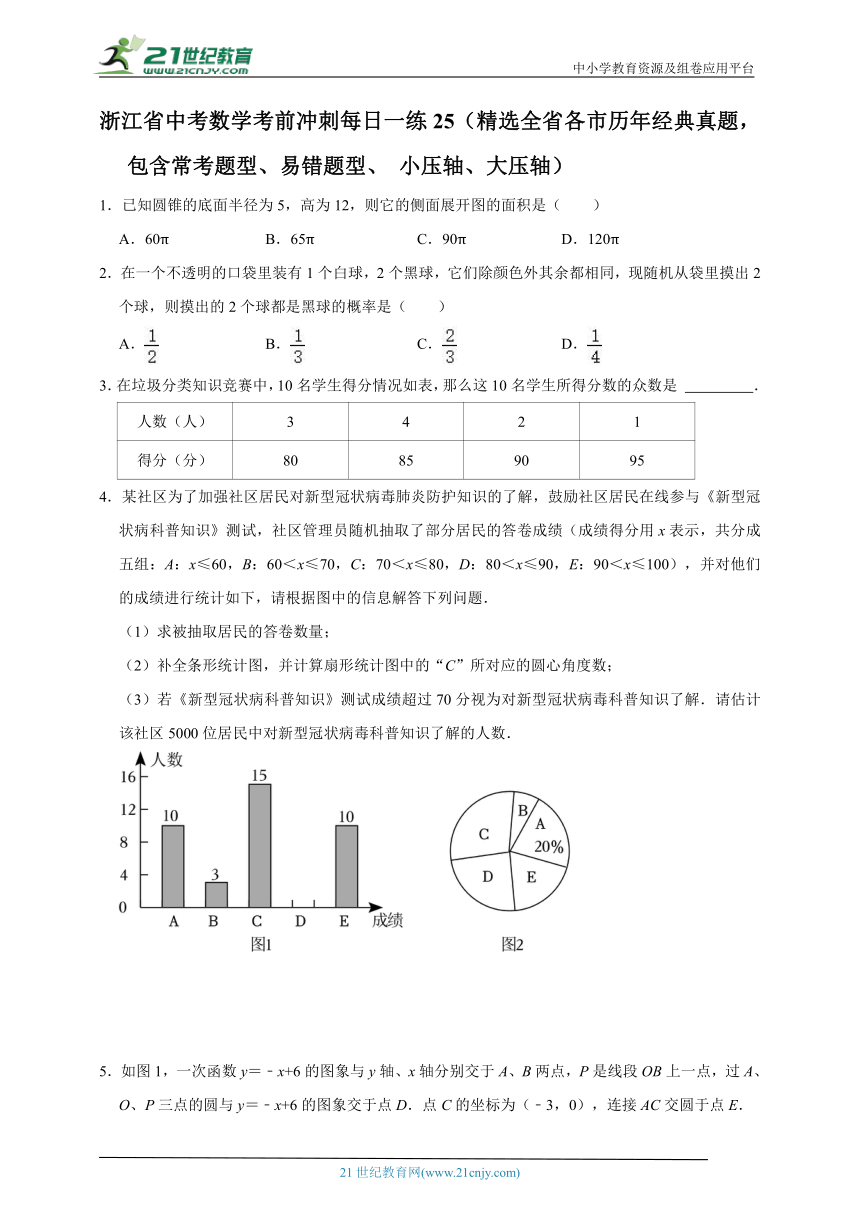 | |
| 格式 | doc | ||
| 文件大小 | 461.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-24 09:27:45 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
浙江省中考数学考前冲刺每日一练25(精选全省各市历年经典真题,包含常考题型、易错题型、 小压轴、大压轴)
1.已知圆锥的底面半径为5,高为12,则它的侧面展开图的面积是( )
A.60π B.65π C.90π D.120π
2.在一个不透明的口袋里装有1个白球,2个黑球,它们除颜色外其余都相同,现随机从袋里摸出2个球,则摸出的2个球都是黑球的概率是( )
A. B. C. D.
3.在垃圾分类知识竞赛中,10名学生得分情况如表,那么这10名学生所得分数的众数是 .
人数(人) 3 4 2 1
得分(分) 80 85 90 95
4.某社区为了加强社区居民对新型冠状病毒肺炎防护知识的了解,鼓励社区居民在线参与《新型冠状病科普知识》测试,社区管理员随机抽取了部分居民的答卷成绩(成绩得分用x表示,共分成五组:A:x≤60,B:60<x≤70,C:70<x≤80,D:80<x≤90,E:90<x≤100),并对他们的成绩进行统计如下,请根据图中的信息解答下列问题.
(1)求被抽取居民的答卷数量;
(2)补全条形统计图,并计算扇形统计图中的“C”所对应的圆心角度数;
(3)若《新型冠状病科普知识》测试成绩超过70分视为对新型冠状病毒科普知识了解.请估计该社区5000位居民中对新型冠状病毒科普知识了解的人数.
5.如图1,一次函数y=﹣x+6的图象与y轴、x轴分别交于A、B两点,P是线段OB上一点,过A、O、P三点的圆与y=﹣x+6的图象交于点D.点C的坐标为(﹣3,0),连接AC交圆于点E.
(1)求∠BAO的度数;
(2)如图2,连接DE,EP,AP,当DE∥BC时,
①判断△AEP的形状,并说明理由;
②求点D的坐标.
(3)如图1,设点P的横坐标为m,的值是否会随m的变化而变化?若变化,请用含m的式子表示;若不变,请求出这个值.
浙江省中考数学考前冲刺每日一练25(精选全省各市历年经典真题,包含常考题型、易错题型、 小压轴、大压轴)参考答案与试题解析
一.选择题(共2小题)
1.已知圆锥的底面半径为5,高为12,则它的侧面展开图的面积是( )
A.60π B.65π C.90π D.120π
【分析】先利用勾股定理求出圆锥侧面展开图扇形的半径,利用侧面展开图与底面圆的关系求出侧面展开图的弧长,再利用扇形面积公式即可求出圆锥侧面展开图的面积.
【解答】解:圆锥侧面展开图扇形的半径为:=13,其弧长为:2×π×5=10π,
∴圆锥侧面展开图的面积为:=65π.
故选:B.
【点评】本题主要考查圆锥的计算,掌握侧面展开图与底面圆的关系是解题关键.
2.在一个不透明的口袋里装有1个白球,2个黑球,它们除颜色外其余都相同,现随机从袋里摸出2个球,则摸出的2个球都是黑球的概率是( )
A. B. C. D.
【分析】先根据题意画出树状图,确定所有可能结果数和符合题意结果数,然后运用概率公式计算即可.
【解答】解:列出树状图如下:
摸出的2个球共有6种可能,其中2个球都是黑球的结果数为2,
所以摸出的2个球都是黑球的概率是.
故选:B.
【点评】本题主要考查了画树状图求概率,正确画出树状图是解答本题的关键.
二.填空题(共1小题)
3.在垃圾分类知识竞赛中,10名学生得分情况如表,那么这10名学生所得分数的众数是 85 .
人数(人) 3 4 2 1
得分(分) 80 85 90 95
【分析】根据众数的定义:一组数据中出现次数最多的数据叫做这组数据的众数进行求解即可.
【解答】解:这10名学生所得分数中,85出现了4次,出现的次数最多,
∴这组数据的众数为85,
故答案为:85.
【点评】本题主要考查了求一组数据的众数,熟知众数的定义是解题的关键.
三.解答题(共2小题)
4.如图1,一次函数y=﹣x+6的图象与y轴、x轴分别交于A、B两点,P是线段OB上一点,过A、O、P三点的圆与y=﹣x+6的图象交于点D.点C的坐标为(﹣3,0),连接AC交圆于点E.
(1)求∠BAO的度数;
(2)如图2,连接DE,EP,AP,当DE∥BC时,
①判断△AEP的形状,并说明理由;
②求点D的坐标.
(3)如图1,设点P的横坐标为m,的值是否会随m的变化而变化?若变化,请用含m的式子表示;若不变,请求出这个值.
【分析】(1)根据一次函数y=﹣x+6的图象与y轴、x轴分别交于A、B两点,得到A(0,6),B(6,0),继而得到OA=OB,根据直角三角形的两个锐角互余计算即可.
(2)①根据平行线的性质,圆周角定理,等腰直角三角形的判定证明即可.
②连接DP,过点D作DF⊥PB于点F,设DE与y轴的交点为G,利用圆周角定理,勾股定理,三角函数计算即可.
(3)先用m表示线段AD,AE,代入化简计算即可.
【解答】解:(1)∵一次函数y=﹣x+6的图象与y轴、x轴分别交于A、B两点,
∴A(0,6),B(6,0),
∴OA=OB,
∴∠OAB=∠OBA=45°,
∴∠BAO=45°.
(2)①∵DE∥BC,∠OAB=∠OBA=45°,
∴∠ADE=∠ABO=∠APE=45°,∠DEP=∠EPO,∠DAP+∠PAO=45°,
∵∠EAO=∠EPO,∠DAP=∠DEP,
∴∠DEP=∠EPO=∠DAP=∠EAO,
∴∠EAO+∠PAO=45°,
∴∠EAP=45°,
∴∠EAP=∠EPA=45°,∠AEP=90°,
∴AE=PE,∠AEP=90°,
∴△AEP是等腰直角三角形.
②如图,过点D作DF⊥PB于点F,设DE与y轴的交点为G,
∵A(0,6),B(6,0),C(﹣3,0),
∴OA=OB=6,OC=3,
在Rt△OAC中,,
在Rt△AEG中,,
设EG=m,则AG=2m,
∴,
∵△AEP是等腰直角三角形,
∴AP是圆的直径,,
∴∠ADP=∠BDP=90°,
∴∠DPB=∠DBP=45°,
∴DP=DB.
∵DE∥BC,∠AOB=90°,
∴∠ADE=∠ABO=∠APE=45°,∠AGD=∠AOB=90°,
∴AG=GD,
∴,
∵∠AGD=∠AOB=∠DFO=90°,
∴四边形OFDG是矩形,
∴OF=DG=AG=2m,BF=DF=OB﹣OF=6﹣2m,
在Rt△BDF中,,
∴,
在Rt△ADP中,AP2=AD2+PD2,
∴,
解得m=2,m=6(舍去),
∴DF=6﹣2m=2,OF=2m=4,
故点D(4,2).
(3)的值是定值,且为9.理由如下:
如图,连接PD,
∵A(0,6),B(6,0),C(﹣3,0),P(m,0),
∴OA=OB=6,OC=3,OP=m,PB=6﹣m,
∴PC=m+3,,,
在Rt△OAC中,,
∵∠AOP=90°,
∴AP是圆的直径,
∴∠ADP=∠BDP=90°,∠CAO=∠CPE,
在Rt△PEC中,,
∴,
∴AE=AC﹣EC=3﹣=,
∵∠ABP=45°,∠BDP=90°,
∴BD=PBsin45°=,
∴AD=AB﹣BD=6﹣=+,
∴AD+AE=3+m+×(12﹣m)=3+m+6﹣m=9,
故的值是定值,且为9.
【点评】本题考查了圆的性质,特殊角的三角函数,解直角三角形,勾股定理,等腰直角三角形的判定和性质,熟练掌握圆的性质,特殊角的三角函数,解直角三角形,勾股定理是解题的关键.
5.某社区为了加强社区居民对新型冠状病毒肺炎防护知识的了解,鼓励社区居民在线参与《新型冠状病科普知识》测试,社区管理员随机抽取了部分居民的答卷成绩(成绩得分用x表示,共分成五组:A:x≤60,B:60<x≤70,C:70<x≤80,D:80<x≤90,E:90<x≤100),并对他们的成绩进行统计如下,请根据图中的信息解答下列问题.
(1)求被抽取居民的答卷数量;
(2)补全条形统计图,并计算扇形统计图中的“C”所对应的圆心角度数;
(3)若《新型冠状病科普知识》测试成绩超过70分视为对新型冠状病毒科普知识了解.请估计该社区5000位居民中对新型冠状病毒科普知识了解的人数.
【分析】(1)根据A组的人数和百分比即可求出被抽取居民的答卷数量;
(2)根据总人数求出D组的人数,即可补全频率分布直方图,用360°乘以C组的百分比即可“C”所对应的圆心角度数;
(3)利用样本估总体,用5000乘以测试成绩超过70分的百分比即可.
【解答】解:(1)10÷20%=50(个),
答:被抽取居民的答卷数量为50个;
(2)D组的人数为50﹣10﹣3﹣15﹣10=12,
扇形统计图中的“C”所对应的圆心角度数为360°×=108°;
补全频率分布直方图如下:
(3)5000×=3700(人).
答:估计该社区5000位居民中对新型冠状病毒科普知识了解的人数为3700人.
【点评】本题考查了条形统计图、扇形统计图、用样本估计总体,解决本题的关键是利用统计图表获取信息.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
浙江省中考数学考前冲刺每日一练25(精选全省各市历年经典真题,包含常考题型、易错题型、 小压轴、大压轴)
1.已知圆锥的底面半径为5,高为12,则它的侧面展开图的面积是( )
A.60π B.65π C.90π D.120π
2.在一个不透明的口袋里装有1个白球,2个黑球,它们除颜色外其余都相同,现随机从袋里摸出2个球,则摸出的2个球都是黑球的概率是( )
A. B. C. D.
3.在垃圾分类知识竞赛中,10名学生得分情况如表,那么这10名学生所得分数的众数是 .
人数(人) 3 4 2 1
得分(分) 80 85 90 95
4.某社区为了加强社区居民对新型冠状病毒肺炎防护知识的了解,鼓励社区居民在线参与《新型冠状病科普知识》测试,社区管理员随机抽取了部分居民的答卷成绩(成绩得分用x表示,共分成五组:A:x≤60,B:60<x≤70,C:70<x≤80,D:80<x≤90,E:90<x≤100),并对他们的成绩进行统计如下,请根据图中的信息解答下列问题.
(1)求被抽取居民的答卷数量;
(2)补全条形统计图,并计算扇形统计图中的“C”所对应的圆心角度数;
(3)若《新型冠状病科普知识》测试成绩超过70分视为对新型冠状病毒科普知识了解.请估计该社区5000位居民中对新型冠状病毒科普知识了解的人数.
5.如图1,一次函数y=﹣x+6的图象与y轴、x轴分别交于A、B两点,P是线段OB上一点,过A、O、P三点的圆与y=﹣x+6的图象交于点D.点C的坐标为(﹣3,0),连接AC交圆于点E.
(1)求∠BAO的度数;
(2)如图2,连接DE,EP,AP,当DE∥BC时,
①判断△AEP的形状,并说明理由;
②求点D的坐标.
(3)如图1,设点P的横坐标为m,的值是否会随m的变化而变化?若变化,请用含m的式子表示;若不变,请求出这个值.
浙江省中考数学考前冲刺每日一练25(精选全省各市历年经典真题,包含常考题型、易错题型、 小压轴、大压轴)参考答案与试题解析
一.选择题(共2小题)
1.已知圆锥的底面半径为5,高为12,则它的侧面展开图的面积是( )
A.60π B.65π C.90π D.120π
【分析】先利用勾股定理求出圆锥侧面展开图扇形的半径,利用侧面展开图与底面圆的关系求出侧面展开图的弧长,再利用扇形面积公式即可求出圆锥侧面展开图的面积.
【解答】解:圆锥侧面展开图扇形的半径为:=13,其弧长为:2×π×5=10π,
∴圆锥侧面展开图的面积为:=65π.
故选:B.
【点评】本题主要考查圆锥的计算,掌握侧面展开图与底面圆的关系是解题关键.
2.在一个不透明的口袋里装有1个白球,2个黑球,它们除颜色外其余都相同,现随机从袋里摸出2个球,则摸出的2个球都是黑球的概率是( )
A. B. C. D.
【分析】先根据题意画出树状图,确定所有可能结果数和符合题意结果数,然后运用概率公式计算即可.
【解答】解:列出树状图如下:
摸出的2个球共有6种可能,其中2个球都是黑球的结果数为2,
所以摸出的2个球都是黑球的概率是.
故选:B.
【点评】本题主要考查了画树状图求概率,正确画出树状图是解答本题的关键.
二.填空题(共1小题)
3.在垃圾分类知识竞赛中,10名学生得分情况如表,那么这10名学生所得分数的众数是 85 .
人数(人) 3 4 2 1
得分(分) 80 85 90 95
【分析】根据众数的定义:一组数据中出现次数最多的数据叫做这组数据的众数进行求解即可.
【解答】解:这10名学生所得分数中,85出现了4次,出现的次数最多,
∴这组数据的众数为85,
故答案为:85.
【点评】本题主要考查了求一组数据的众数,熟知众数的定义是解题的关键.
三.解答题(共2小题)
4.如图1,一次函数y=﹣x+6的图象与y轴、x轴分别交于A、B两点,P是线段OB上一点,过A、O、P三点的圆与y=﹣x+6的图象交于点D.点C的坐标为(﹣3,0),连接AC交圆于点E.
(1)求∠BAO的度数;
(2)如图2,连接DE,EP,AP,当DE∥BC时,
①判断△AEP的形状,并说明理由;
②求点D的坐标.
(3)如图1,设点P的横坐标为m,的值是否会随m的变化而变化?若变化,请用含m的式子表示;若不变,请求出这个值.
【分析】(1)根据一次函数y=﹣x+6的图象与y轴、x轴分别交于A、B两点,得到A(0,6),B(6,0),继而得到OA=OB,根据直角三角形的两个锐角互余计算即可.
(2)①根据平行线的性质,圆周角定理,等腰直角三角形的判定证明即可.
②连接DP,过点D作DF⊥PB于点F,设DE与y轴的交点为G,利用圆周角定理,勾股定理,三角函数计算即可.
(3)先用m表示线段AD,AE,代入化简计算即可.
【解答】解:(1)∵一次函数y=﹣x+6的图象与y轴、x轴分别交于A、B两点,
∴A(0,6),B(6,0),
∴OA=OB,
∴∠OAB=∠OBA=45°,
∴∠BAO=45°.
(2)①∵DE∥BC,∠OAB=∠OBA=45°,
∴∠ADE=∠ABO=∠APE=45°,∠DEP=∠EPO,∠DAP+∠PAO=45°,
∵∠EAO=∠EPO,∠DAP=∠DEP,
∴∠DEP=∠EPO=∠DAP=∠EAO,
∴∠EAO+∠PAO=45°,
∴∠EAP=45°,
∴∠EAP=∠EPA=45°,∠AEP=90°,
∴AE=PE,∠AEP=90°,
∴△AEP是等腰直角三角形.
②如图,过点D作DF⊥PB于点F,设DE与y轴的交点为G,
∵A(0,6),B(6,0),C(﹣3,0),
∴OA=OB=6,OC=3,
在Rt△OAC中,,
在Rt△AEG中,,
设EG=m,则AG=2m,
∴,
∵△AEP是等腰直角三角形,
∴AP是圆的直径,,
∴∠ADP=∠BDP=90°,
∴∠DPB=∠DBP=45°,
∴DP=DB.
∵DE∥BC,∠AOB=90°,
∴∠ADE=∠ABO=∠APE=45°,∠AGD=∠AOB=90°,
∴AG=GD,
∴,
∵∠AGD=∠AOB=∠DFO=90°,
∴四边形OFDG是矩形,
∴OF=DG=AG=2m,BF=DF=OB﹣OF=6﹣2m,
在Rt△BDF中,,
∴,
在Rt△ADP中,AP2=AD2+PD2,
∴,
解得m=2,m=6(舍去),
∴DF=6﹣2m=2,OF=2m=4,
故点D(4,2).
(3)的值是定值,且为9.理由如下:
如图,连接PD,
∵A(0,6),B(6,0),C(﹣3,0),P(m,0),
∴OA=OB=6,OC=3,OP=m,PB=6﹣m,
∴PC=m+3,,,
在Rt△OAC中,,
∵∠AOP=90°,
∴AP是圆的直径,
∴∠ADP=∠BDP=90°,∠CAO=∠CPE,
在Rt△PEC中,,
∴,
∴AE=AC﹣EC=3﹣=,
∵∠ABP=45°,∠BDP=90°,
∴BD=PBsin45°=,
∴AD=AB﹣BD=6﹣=+,
∴AD+AE=3+m+×(12﹣m)=3+m+6﹣m=9,
故的值是定值,且为9.
【点评】本题考查了圆的性质,特殊角的三角函数,解直角三角形,勾股定理,等腰直角三角形的判定和性质,熟练掌握圆的性质,特殊角的三角函数,解直角三角形,勾股定理是解题的关键.
5.某社区为了加强社区居民对新型冠状病毒肺炎防护知识的了解,鼓励社区居民在线参与《新型冠状病科普知识》测试,社区管理员随机抽取了部分居民的答卷成绩(成绩得分用x表示,共分成五组:A:x≤60,B:60<x≤70,C:70<x≤80,D:80<x≤90,E:90<x≤100),并对他们的成绩进行统计如下,请根据图中的信息解答下列问题.
(1)求被抽取居民的答卷数量;
(2)补全条形统计图,并计算扇形统计图中的“C”所对应的圆心角度数;
(3)若《新型冠状病科普知识》测试成绩超过70分视为对新型冠状病毒科普知识了解.请估计该社区5000位居民中对新型冠状病毒科普知识了解的人数.
【分析】(1)根据A组的人数和百分比即可求出被抽取居民的答卷数量;
(2)根据总人数求出D组的人数,即可补全频率分布直方图,用360°乘以C组的百分比即可“C”所对应的圆心角度数;
(3)利用样本估总体,用5000乘以测试成绩超过70分的百分比即可.
【解答】解:(1)10÷20%=50(个),
答:被抽取居民的答卷数量为50个;
(2)D组的人数为50﹣10﹣3﹣15﹣10=12,
扇形统计图中的“C”所对应的圆心角度数为360°×=108°;
补全频率分布直方图如下:
(3)5000×=3700(人).
答:估计该社区5000位居民中对新型冠状病毒科普知识了解的人数为3700人.
【点评】本题考查了条形统计图、扇形统计图、用样本估计总体,解决本题的关键是利用统计图表获取信息.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
