浙江省中考数学考前冲刺每日一练24(精选全省各市历年经典真题,包含常考题型、易错题型、 小压轴、大压轴)
文档属性
| 名称 | 浙江省中考数学考前冲刺每日一练24(精选全省各市历年经典真题,包含常考题型、易错题型、 小压轴、大压轴) | 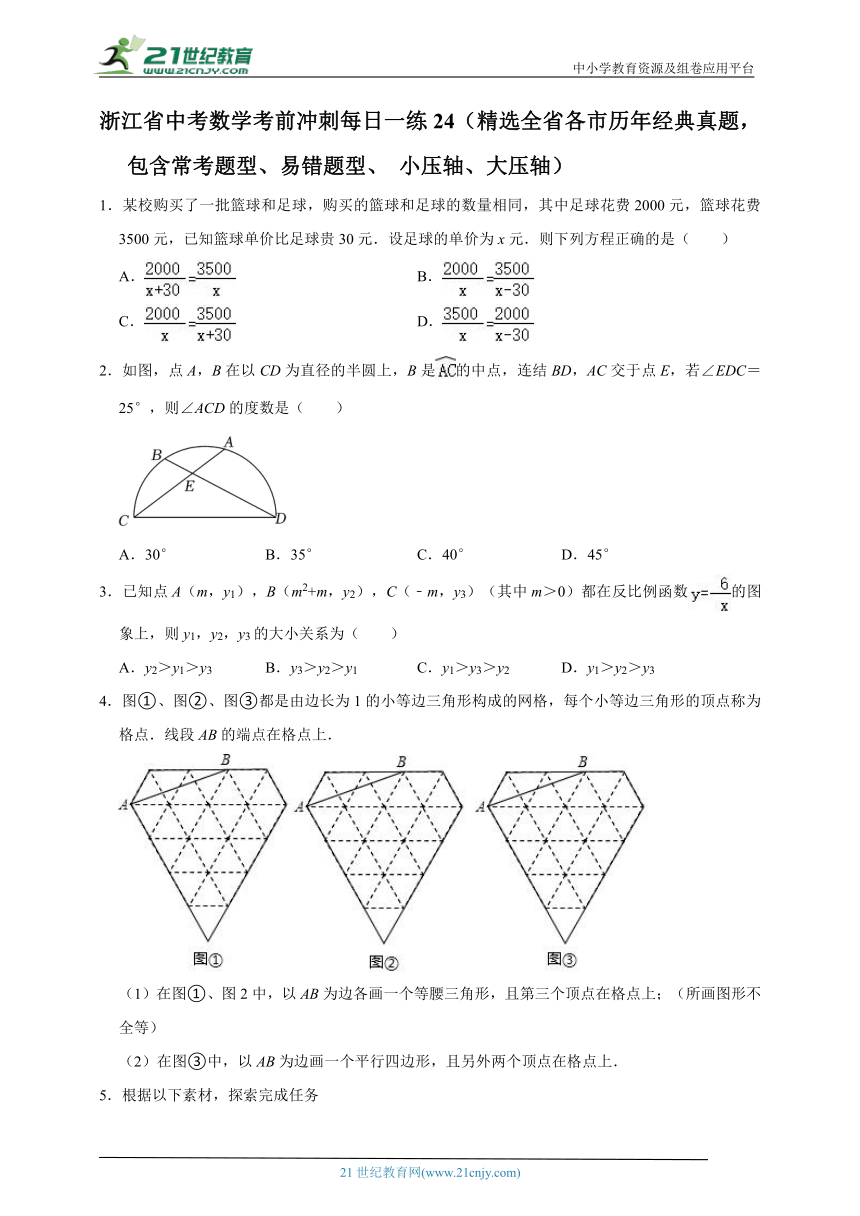 | |
| 格式 | doc | ||
| 文件大小 | 381.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-24 09:27:45 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
浙江省中考数学考前冲刺每日一练24(精选全省各市历年经典真题,包含常考题型、易错题型、 小压轴、大压轴)
1.某校购买了一批篮球和足球,购买的篮球和足球的数量相同,其中足球花费2000元,篮球花费3500元,已知篮球单价比足球贵30元.设足球的单价为x元.则下列方程正确的是( )
A. B.
C. D.
2.如图,点A,B在以CD为直径的半圆上,B是的中点,连结BD,AC交于点E,若∠EDC=25°,则∠ACD的度数是( )
A.30° B.35° C.40° D.45°
3.已知点A(m,y1),B(m2+m,y2),C(﹣m,y3)(其中m>0)都在反比例函数的图象上,则y1,y2,y3的大小关系为( )
A.y2>y1>y3 B.y3>y2>y1 C.y1>y3>y2 D.y1>y2>y3
4.图①、图②、图③都是由边长为1的小等边三角形构成的网格,每个小等边三角形的顶点称为格点.线段AB的端点在格点上.
(1)在图①、图2中,以AB为边各画一个等腰三角形,且第三个顶点在格点上;(所画图形不全等)
(2)在图③中,以AB为边画一个平行四边形,且另外两个顶点在格点上.
5.根据以下素材,探索完成任务
如何设计购买方案?
素材1 某校40名同学要去参观航天展览馆,已知展览馆分为A,B,C三个场馆,且购买1张A场馆门票和1张B场馆门票共需90元,购买3张A场馆门票和2张B场馆门票共需230元.C场馆门票为每张15元.
素材2 由于场地原因,要求到A场馆参观的人数要少于到B场馆参观的人数,且每位同学只能选择一个场馆参观.参观当天刚好有优惠活动:每购买1张A场馆门票就赠送1张C场馆门票.
问题解决
任务1 确定场馆门票价格 求A场馆和B场馆的门票价格.
任务2 探究经费的使用 若购买A场馆的门票赠送的C场馆门票刚好够参观C场馆的同学使用,求此次购买门票所需总金额的最小值.
任务3 拟定购买方案 若购买门票总预算为1100元,在不超额的前提下,要让去A场馆的人数尽量的多,请你设计一种购买方案. 购买方案门票类型ABC购买数量
浙江省中考数学考前冲刺每日一练24(精选全省各市历年经典真题,包含常考题型、易错题型、 小压轴、大压轴)参考答案与试题解析
一.选择题(共3小题)
1.某校购买了一批篮球和足球,购买的篮球和足球的数量相同,其中足球花费2000元,篮球花费3500元,已知篮球单价比足球贵30元.设足球的单价为x元.则下列方程正确的是( )
A. B.
C. D.
【分析】设足球的单价为x元.根据其中足球花费2000元,篮球花费3500元,已知篮球单价比足球贵30元解方程即可得到结论.
【解答】解:根据题意得,,
故选:C.
【点评】本题考查了由实际问题抽象出分式方程,找准等量关系,正确列出分式方程是解题的关键.
2.如图,点A,B在以CD为直径的半圆上,B是的中点,连结BD,AC交于点E,若∠EDC=25°,则∠ACD的度数是( )
A.30° B.35° C.40° D.45°
【分析】连接AD,由圆周角定理得到∠DAC=90°,∠CDE=∠EDA=25°,由直角三角形的性质即可求出∠ACD的度数.
【解答】解:连接AD,
∵CD是圆的直径,
∴∠DAC=90°,
∵B是的中点,
∴∠CDE=∠EDA=25°,
∴∠ADC=50°,
∴∠ACD=90°﹣∠ADC=40°.
故选:C.
【点评】本题考查圆周角定理,直角三角形的性质,关键是掌握圆周角定理.
3.已知点A(m,y1),B(m2+m,y2),C(﹣m,y3)(其中m>0)都在反比例函数的图象上,则y1,y2,y3的大小关系为( )
A.y2>y1>y3 B.y3>y2>y1 C.y1>y3>y2 D.y1>y2>y3
【分析】根据反比例函数图象上点的坐标特征分别计算出y1、y2、y3的值,然后比较大小即可.
【解答】解:∵A(m,y1),B(m2+m,y2),C(﹣m,y3)(其中m>0)都在反比例函数y=的图象上,
∴y1=,y2=,y3=,
∵m2+m>m>0,
∴0>y2>y1,
∵y3>0,
∴y3>y2>y1,
故选:B.
【点评】本题考查了反比例函数图象上点的坐标特征:反比例函数y=(k为常数,k≠0)的图象是双曲线,图象上的点(x,y)的横纵坐标的积是定值k,即xy=k.
二.解答题(共2小题)
4.图①、图②、图③都是由边长为1的小等边三角形构成的网格,每个小等边三角形的顶点称为格点.线段AB的端点在格点上.
(1)在图①、图2中,以AB为边各画一个等腰三角形,且第三个顶点在格点上;(所画图形不全等)
(2)在图③中,以AB为边画一个平行四边形,且另外两个顶点在格点上.
【分析】(1)作线段AB的垂直平分线,垂直平分线经过的格点即为等腰三角形的第三个顶点;以点A为圆心,以AB的长为半径画弧,弧线经过的格点即为等腰三角形的第三个顶点.
(2)将点A沿任意方向平移到另一格点处,然后将点B也按相同的方法平移,最后连接点A、B及点B、A的对应点即可.
【解答】解:(1)如图①、②所示,△ABC和△ABD即为所求;
(2)如图③所示, ABFE即为所求.
【点评】本题主要考查作图﹣应用与设计作图,熟练掌握等腰三角形的定义和平行四边形的判定是解题的关键.
5.根据以下素材,探索完成任务
如何设计购买方案?
素材1 某校40名同学要去参观航天展览馆,已知展览馆分为A,B,C三个场馆,且购买1张A场馆门票和1张B场馆门票共需90元,购买3张A场馆门票和2张B场馆门票共需230元.C场馆门票为每张15元.
素材2 由于场地原因,要求到A场馆参观的人数要少于到B场馆参观的人数,且每位同学只能选择一个场馆参观.参观当天刚好有优惠活动:每购买1张A场馆门票就赠送1张C场馆门票.
问题解决
任务1 确定场馆门票价格 求A场馆和B场馆的门票价格.
任务2 探究经费的使用 若购买A场馆的门票赠送的C场馆门票刚好够参观C场馆的同学使用,求此次购买门票所需总金额的最小值.
任务3 拟定购买方案 若购买门票总预算为1100元,在不超额的前提下,要让去A场馆的人数尽量的多,请你设计一种购买方案. 购买方案门票类型ABC购买数量
【分析】(1)设A场馆门票为x元,B场馆门票为y元,再根据文中数量关系列出等量关系式即可得出结论.
(2)购买A场馆门票a张,则购买B场馆门票(40﹣2a)张,依题意得:α<40﹣2a求出a的取值范围,再设此次购买门票所需总金额为w元,则有w=50a+40(40﹣2a)=﹣30a+1600,最后根据函数系数a的性质确定最值问题.
(3)设购买A场馆门票m张,C场馆门票n张,则购买B场馆门票(40﹣2m﹣n),根据文中数量关系列出50m+40(40﹣2m﹣n)+15n=1100,则n=20﹣,根据m、n为正整数这一条件判断m、n的值即可得出结论,最后要记得检验是否符合题意.
【解答】(1)解:设A场馆门票为x元,B场馆门票为y元,
,解得.
答:A场馆门票的单价为50元,B场馆门票的单价40元.
(2)设购买A场馆门票a张,则购买B场馆门票(40﹣2a)张,
依题意得:α<40﹣2a,解得:a<.
设此次购买门票所需总金额为w元,则
w=50a+40(40﹣2a)=﹣30a+1600,
∵﹣30<0,
∴w随a的增大而减小.
∵a<,且a为整数,
∴当a=13时,w取得最小值,最小值=﹣30×13+1600=1210.
答:此次购买门票所需总金额的最小值为1210元.
(3)设购买A场馆门票m张,C场馆门票n张,则购买B场馆门票(40﹣2m﹣n),
依题意得:
50m+40(40﹣2m﹣n)+15n=1100,
∴n=20﹣.
又∵m,n均为正整数,
∴或或.
当m=5,n=14时,40﹣2m﹣n=40﹣2×5﹣14=16>5,符合题意.
当m=10,n=8时,40﹣2m﹣n=40﹣2×10﹣8=12>10,符合题意.
当m=15,n=2时,40﹣2m﹣n=40﹣2×15﹣2=8<15,符合题意,舍去;
∴共有2种购买方案,
方案1:购买5张A场馆门票,16张B场馆门票,14张C场馆门票;
方案2:购买10张A场馆门票,12张B场馆门票,8张C场馆门票.
又∵在不超额的前提下,要让去A场馆的人数尽量的多,
∴选择方案2,
即购买10张A场馆门票,12张B场馆门票,8张C场馆门票.
【点评】本题考查了二元一次方程组,不等式的应用以及最值问题,对学生的综合能力要求较高.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
浙江省中考数学考前冲刺每日一练24(精选全省各市历年经典真题,包含常考题型、易错题型、 小压轴、大压轴)
1.某校购买了一批篮球和足球,购买的篮球和足球的数量相同,其中足球花费2000元,篮球花费3500元,已知篮球单价比足球贵30元.设足球的单价为x元.则下列方程正确的是( )
A. B.
C. D.
2.如图,点A,B在以CD为直径的半圆上,B是的中点,连结BD,AC交于点E,若∠EDC=25°,则∠ACD的度数是( )
A.30° B.35° C.40° D.45°
3.已知点A(m,y1),B(m2+m,y2),C(﹣m,y3)(其中m>0)都在反比例函数的图象上,则y1,y2,y3的大小关系为( )
A.y2>y1>y3 B.y3>y2>y1 C.y1>y3>y2 D.y1>y2>y3
4.图①、图②、图③都是由边长为1的小等边三角形构成的网格,每个小等边三角形的顶点称为格点.线段AB的端点在格点上.
(1)在图①、图2中,以AB为边各画一个等腰三角形,且第三个顶点在格点上;(所画图形不全等)
(2)在图③中,以AB为边画一个平行四边形,且另外两个顶点在格点上.
5.根据以下素材,探索完成任务
如何设计购买方案?
素材1 某校40名同学要去参观航天展览馆,已知展览馆分为A,B,C三个场馆,且购买1张A场馆门票和1张B场馆门票共需90元,购买3张A场馆门票和2张B场馆门票共需230元.C场馆门票为每张15元.
素材2 由于场地原因,要求到A场馆参观的人数要少于到B场馆参观的人数,且每位同学只能选择一个场馆参观.参观当天刚好有优惠活动:每购买1张A场馆门票就赠送1张C场馆门票.
问题解决
任务1 确定场馆门票价格 求A场馆和B场馆的门票价格.
任务2 探究经费的使用 若购买A场馆的门票赠送的C场馆门票刚好够参观C场馆的同学使用,求此次购买门票所需总金额的最小值.
任务3 拟定购买方案 若购买门票总预算为1100元,在不超额的前提下,要让去A场馆的人数尽量的多,请你设计一种购买方案. 购买方案门票类型ABC购买数量
浙江省中考数学考前冲刺每日一练24(精选全省各市历年经典真题,包含常考题型、易错题型、 小压轴、大压轴)参考答案与试题解析
一.选择题(共3小题)
1.某校购买了一批篮球和足球,购买的篮球和足球的数量相同,其中足球花费2000元,篮球花费3500元,已知篮球单价比足球贵30元.设足球的单价为x元.则下列方程正确的是( )
A. B.
C. D.
【分析】设足球的单价为x元.根据其中足球花费2000元,篮球花费3500元,已知篮球单价比足球贵30元解方程即可得到结论.
【解答】解:根据题意得,,
故选:C.
【点评】本题考查了由实际问题抽象出分式方程,找准等量关系,正确列出分式方程是解题的关键.
2.如图,点A,B在以CD为直径的半圆上,B是的中点,连结BD,AC交于点E,若∠EDC=25°,则∠ACD的度数是( )
A.30° B.35° C.40° D.45°
【分析】连接AD,由圆周角定理得到∠DAC=90°,∠CDE=∠EDA=25°,由直角三角形的性质即可求出∠ACD的度数.
【解答】解:连接AD,
∵CD是圆的直径,
∴∠DAC=90°,
∵B是的中点,
∴∠CDE=∠EDA=25°,
∴∠ADC=50°,
∴∠ACD=90°﹣∠ADC=40°.
故选:C.
【点评】本题考查圆周角定理,直角三角形的性质,关键是掌握圆周角定理.
3.已知点A(m,y1),B(m2+m,y2),C(﹣m,y3)(其中m>0)都在反比例函数的图象上,则y1,y2,y3的大小关系为( )
A.y2>y1>y3 B.y3>y2>y1 C.y1>y3>y2 D.y1>y2>y3
【分析】根据反比例函数图象上点的坐标特征分别计算出y1、y2、y3的值,然后比较大小即可.
【解答】解:∵A(m,y1),B(m2+m,y2),C(﹣m,y3)(其中m>0)都在反比例函数y=的图象上,
∴y1=,y2=,y3=,
∵m2+m>m>0,
∴0>y2>y1,
∵y3>0,
∴y3>y2>y1,
故选:B.
【点评】本题考查了反比例函数图象上点的坐标特征:反比例函数y=(k为常数,k≠0)的图象是双曲线,图象上的点(x,y)的横纵坐标的积是定值k,即xy=k.
二.解答题(共2小题)
4.图①、图②、图③都是由边长为1的小等边三角形构成的网格,每个小等边三角形的顶点称为格点.线段AB的端点在格点上.
(1)在图①、图2中,以AB为边各画一个等腰三角形,且第三个顶点在格点上;(所画图形不全等)
(2)在图③中,以AB为边画一个平行四边形,且另外两个顶点在格点上.
【分析】(1)作线段AB的垂直平分线,垂直平分线经过的格点即为等腰三角形的第三个顶点;以点A为圆心,以AB的长为半径画弧,弧线经过的格点即为等腰三角形的第三个顶点.
(2)将点A沿任意方向平移到另一格点处,然后将点B也按相同的方法平移,最后连接点A、B及点B、A的对应点即可.
【解答】解:(1)如图①、②所示,△ABC和△ABD即为所求;
(2)如图③所示, ABFE即为所求.
【点评】本题主要考查作图﹣应用与设计作图,熟练掌握等腰三角形的定义和平行四边形的判定是解题的关键.
5.根据以下素材,探索完成任务
如何设计购买方案?
素材1 某校40名同学要去参观航天展览馆,已知展览馆分为A,B,C三个场馆,且购买1张A场馆门票和1张B场馆门票共需90元,购买3张A场馆门票和2张B场馆门票共需230元.C场馆门票为每张15元.
素材2 由于场地原因,要求到A场馆参观的人数要少于到B场馆参观的人数,且每位同学只能选择一个场馆参观.参观当天刚好有优惠活动:每购买1张A场馆门票就赠送1张C场馆门票.
问题解决
任务1 确定场馆门票价格 求A场馆和B场馆的门票价格.
任务2 探究经费的使用 若购买A场馆的门票赠送的C场馆门票刚好够参观C场馆的同学使用,求此次购买门票所需总金额的最小值.
任务3 拟定购买方案 若购买门票总预算为1100元,在不超额的前提下,要让去A场馆的人数尽量的多,请你设计一种购买方案. 购买方案门票类型ABC购买数量
【分析】(1)设A场馆门票为x元,B场馆门票为y元,再根据文中数量关系列出等量关系式即可得出结论.
(2)购买A场馆门票a张,则购买B场馆门票(40﹣2a)张,依题意得:α<40﹣2a求出a的取值范围,再设此次购买门票所需总金额为w元,则有w=50a+40(40﹣2a)=﹣30a+1600,最后根据函数系数a的性质确定最值问题.
(3)设购买A场馆门票m张,C场馆门票n张,则购买B场馆门票(40﹣2m﹣n),根据文中数量关系列出50m+40(40﹣2m﹣n)+15n=1100,则n=20﹣,根据m、n为正整数这一条件判断m、n的值即可得出结论,最后要记得检验是否符合题意.
【解答】(1)解:设A场馆门票为x元,B场馆门票为y元,
,解得.
答:A场馆门票的单价为50元,B场馆门票的单价40元.
(2)设购买A场馆门票a张,则购买B场馆门票(40﹣2a)张,
依题意得:α<40﹣2a,解得:a<.
设此次购买门票所需总金额为w元,则
w=50a+40(40﹣2a)=﹣30a+1600,
∵﹣30<0,
∴w随a的增大而减小.
∵a<,且a为整数,
∴当a=13时,w取得最小值,最小值=﹣30×13+1600=1210.
答:此次购买门票所需总金额的最小值为1210元.
(3)设购买A场馆门票m张,C场馆门票n张,则购买B场馆门票(40﹣2m﹣n),
依题意得:
50m+40(40﹣2m﹣n)+15n=1100,
∴n=20﹣.
又∵m,n均为正整数,
∴或或.
当m=5,n=14时,40﹣2m﹣n=40﹣2×5﹣14=16>5,符合题意.
当m=10,n=8时,40﹣2m﹣n=40﹣2×10﹣8=12>10,符合题意.
当m=15,n=2时,40﹣2m﹣n=40﹣2×15﹣2=8<15,符合题意,舍去;
∴共有2种购买方案,
方案1:购买5张A场馆门票,16张B场馆门票,14张C场馆门票;
方案2:购买10张A场馆门票,12张B场馆门票,8张C场馆门票.
又∵在不超额的前提下,要让去A场馆的人数尽量的多,
∴选择方案2,
即购买10张A场馆门票,12张B场馆门票,8张C场馆门票.
【点评】本题考查了二元一次方程组,不等式的应用以及最值问题,对学生的综合能力要求较高.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
