浙江省中考数学考前冲刺每日一练26(精选全省各市历年经典真题,包含常考题型、易错题型、 小压轴、大压轴)
文档属性
| 名称 | 浙江省中考数学考前冲刺每日一练26(精选全省各市历年经典真题,包含常考题型、易错题型、 小压轴、大压轴) |  | |
| 格式 | doc | ||
| 文件大小 | 542.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-24 09:27:45 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
浙江省中考数学考前冲刺每日一练26(精选全省各市历年经典真题,包含常考题型、易错题型、 小压轴、大压轴)
1.据中国宁波网消息:2023年一季度宁波全市实现地区生产总值380180000000元,同比增长4.5%.数380180000000用科学记数法表示为( )
A.0.38018×1012 B.3.8018×1011
C.3.8018×1010 D.38.018×1010
2.一个不透明的袋子里装有3个绿球、3个黑球和6个红球,它们除颜色外其余相同.从袋中任意摸出一个球为绿球的概率为 .
3.如图,在Rt△ABC中,∠C=90°,E为AB边上一点,以AE为直径的半圆O与BC相切于点D,连结AD,BE=3,BD=3.P是AB边上的动点,当△ADP为等腰三角形时,AP的长为 .
4.在4×4的方格纸中,请按下列要求画出格点三角形(顶点均在格点上).
(1)在图1中先画出一个以格点P为顶点的等腰三角形PAB,再画出该三角形向右平移2个单位后的△P′A′B′.
(2)将图2中的格点△ABC绕点C按顺时针方向旋转90°,画出经旋转后的△A′B′C.
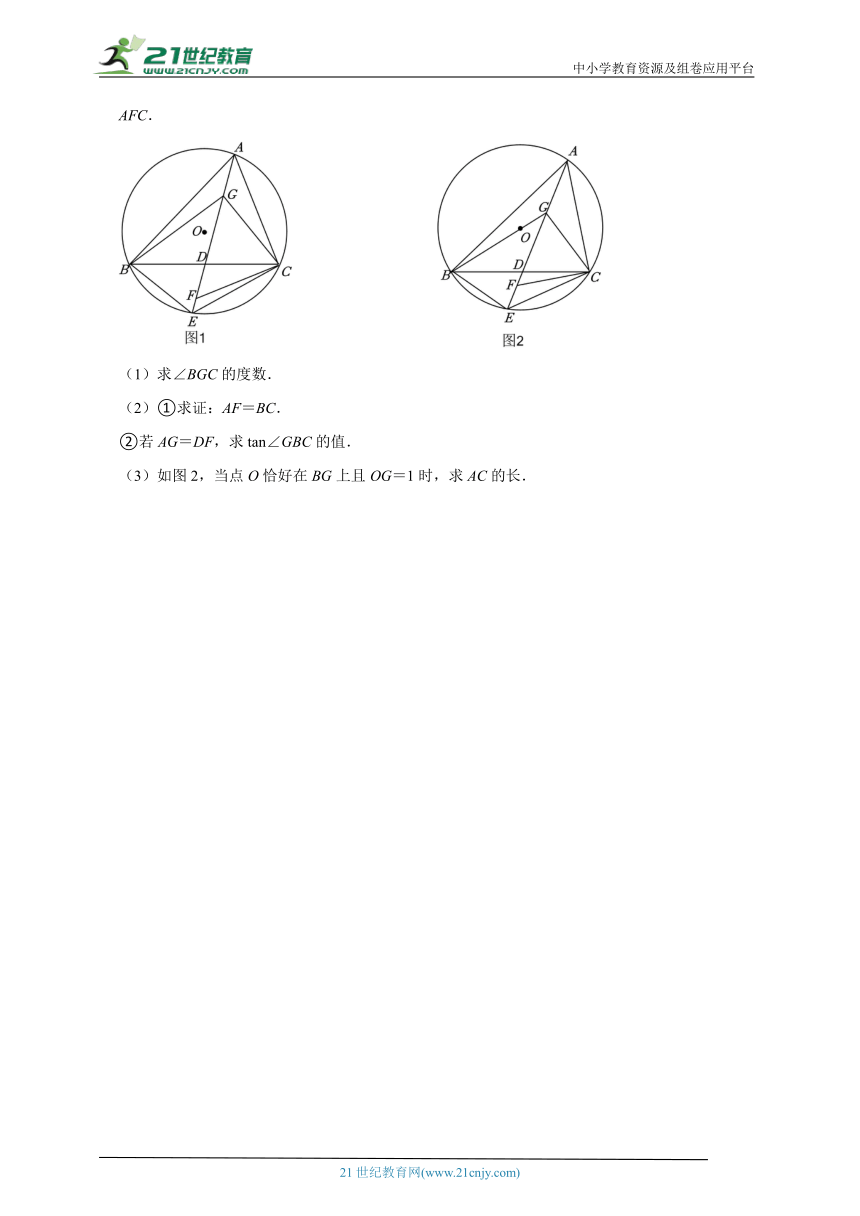
5.如图1,锐角△ABC内接于⊙O,D为BC的中点,连结AD并延长交⊙O于点E,连结BE,CE,过C作AC的垂线交AE于点F,点G在AD上,连结BG,CG,若BC平分∠EBG且∠BCG=∠AFC.
(1)求∠BGC的度数.
(2)①求证:AF=BC.
②若AG=DF,求tan∠GBC的值.
(3)如图2,当点O恰好在BG上且OG=1时,求AC的长.
浙江省中考数学考前冲刺每日一练26(精选全省各市历年经典真题,包含常考题型、易错题型、 小压轴、大压轴)参考答案与试题解析
一.选择题(共1小题)
1.据中国宁波网消息:2023年一季度宁波全市实现地区生产总值380180000000元,同比增长4.5%.数380180000000用科学记数法表示为( )
A.0.38018×1012 B.3.8018×1011
C.3.8018×1010 D.38.018×1010
【分析】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值≥10时,n是正整数;当原数的绝对值<1时,n是负整数.
【解答】解:380180000000=3.8018×1011.
故选:B.
【点评】此题考查科学记数法的表示方法.科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数,表示时关键要正确确定a的值以及n的值.
二.填空题(共2小题)
2.一个不透明的袋子里装有3个绿球、3个黑球和6个红球,它们除颜色外其余相同.从袋中任意摸出一个球为绿球的概率为 .
【分析】根据概率公式可知,用绿球的个数除以球的总数即可.
【解答】解:∵袋子里装有3个绿球、3个黑球和6个红球,
∴从袋中任意摸出一个球是绿球的概率为.
故答案为:.
【点评】此题考查了概率公式,熟知概率=所求情况数与总情况数之比是解题的关键.
3.如图,在Rt△ABC中,∠C=90°,E为AB边上一点,以AE为直径的半圆O与BC相切于点D,连结AD,BE=3,BD=3.P是AB边上的动点,当△ADP为等腰三角形时,AP的长为 6或2 .
【分析】连接OD,DE,根据切线的性质和勾股定理求出OD=6,然后分三种情况讨论:①当AP=PD时,此时P与O重合,②如图2,当AP′=AD时,③如图3,当DP′′=AD时,分别进行求解即可.
【解答】解:如图1,连接OD,DE,
∵半圆O与BC相切于点D,
∴OD⊥BC,
在Rt△OBD中,OB=OE+BE=OD+3,BD=3.
∴OB2=BD2+OD2,
∴(OD+3)2=(3)2+OD2,
解得OD=6,
∴AO=EO=OD=6,
①当AP=PD时,此时P与O重合,
∴AP=AO=6;
②如图2,当AP′=AD时,
在Rt△ABC中,
∵∠C=90°,
∴AC⊥BC,
∴OD∥AC,
∴△BOD∽△BAC,
∴==,
∴==,
∴AC=10,CD=2,
∴AD===2,
∴AP′=AD=2;
③如图3,当DP′′=AD时,
∵AD=2,
∴DP′′=AD=2,
∵OD=OA,
∴∠ODA=∠BAD,
∴OD∥AC,
∴∠ODA=∠CAD,
∴∠BAD=∠CAD,
∴AD平分∠BAC,
过点D作DH⊥AE于点H,
∴AH=P″H,DH=DC=2,
∵AD=AD,
∴Rt△ADH≌Rt△ADC(HL),
∴AH=AC=10,
∴AH=AC=P″H=10,
∴AP″=2AH=20(P为AB边上一点,不符合题意,舍去),
综上所述:当△ADP为等腰三角形时,AP的长为6或2.
故答案为:6或2.
【点评】此题属于圆的综合题,考查了切线的性质,圆周角定理,勾股定理,相似三角形的判定与性质,全等三角形的判定与性质,等腰三角形的性质,综合性强,解决本题的关键是利用分类讨论思想.
三.解答题(共2小题)
4.在4×4的方格纸中,请按下列要求画出格点三角形(顶点均在格点上).
(1)在图1中先画出一个以格点P为顶点的等腰三角形PAB,再画出该三角形向右平移2个单位后的△P′A′B′.
(2)将图2中的格点△ABC绕点C按顺时针方向旋转90°,画出经旋转后的△A′B′C.
【分析】(1)根据等腰三角形的定义,平移变换的性质作出图形即可;
(2)根据旋转变换的性质作出图形即可.
【解答】解:(1)如图1,△P′A′B′即为所求;
(2)如图2,△A′B′C即为所求.
【点评】本题考查作图﹣旋转变换,平移变换,等腰三角形的性质等知识,解题的关键是理解题意,灵活运用所学知识解决问题.
5.如图1,锐角△ABC内接于⊙O,D为BC的中点,连结AD并延长交⊙O于点E,连结BE,CE,过C作AC的垂线交AE于点F,点G在AD上,连结BG,CG,若BC平分∠EBG且∠BCG=∠AFC.
(1)求∠BGC的度数.
(2)①求证:AF=BC.
②若AG=DF,求tan∠GBC的值.
(3)如图2,当点O恰好在BG上且OG=1时,求AC的长.
【分析】(1)根据同弧圆周角相等得∠EBC=∠EAC,然后利用直角三角形两个锐角互余即可解决问题;
(2)①证明△ACF≌△BGC(ASA),即可解决问题;
②过点C作CH⊥EG于点H,设AG=DF=2x,根据勾股定理和锐角三角函数即可解决问题;
(3)过点O作OM⊥BE于点M,连结OC交AE于点N,分别证明△EBD≌△NCD(ASA),△COG≌△OBM(AAS),得BM=OG=1,设OB=OC=r,然后由△GON∽△GBE,对应边成比例,求出r的值,进而可求AC的长.
【解答】(1)解:∵BC平分∠EBG,
∴∠EBC=∠CBG,
∵∠EBC=∠EAC,
∴∠CBG=∠EAC,
∵AC⊥FC,
∴∠AFC+∠EAC=90°,
∵∠BCG=∠AFC,
∴∠BCG+∠CBG=90°,
∴∠BGC=90°;
(2)①证明:∵∠BGC=90°,D为BC中点,
∴GD=CD,
∴∠DGC=∠DCG,
∵∠BCG=∠AFC,
∴∠DGC=∠AFC,
∴CF=CG,
∵∠ACF=∠BGC=90°,
∴△ACF≌△BGC(ASA),
∴AF=BC;
②解:如图1,过点C作CH⊥EG于点H,
设AG=DF=2x,
∵△ACF≌△BGC,
∴AF=BC=2DG,
∴CD=DG=AG+DF=4x,
∵CF=CG,
∴HG=HF=3x,
∴DH=x,AH=5x,
∴CH===x,
∴tan∠GBC=tan∠CAF==,
∴tan∠GBC的值为;
(3)解:如图2,过点O作OM⊥BE于点M,连结OC交AE于点N,
∵OB=OC,
∴∠CBE=∠OBC=∠OCB,
∴OC∥BE,
∵BD=CD,∠BDE=∠CDN,
∴△EBD≌△NCD(ASA),
∴BE=CN,
∵OC∥BE,
∴∠GOC=∠MBO,
∵∠CGO=∠OMB=90°,OC=OB,
∴△COG≌△OBM(AAS),
∴BM=OG=1,
∵OM⊥BE,
∴CN=BE=2BM=2,
设OB=OC=r,
∵OC∥BE,
∴△GON∽△GBE,
∴=,
∴=,
解得r=或r=(舍去),
由(2)知:△ACF≌△BGC,
∴AC=BG=BO+OG=r+1=.
∴AC的长为.
【点评】本题属于圆综合题,考查了垂径定理,圆周角定理,相似三角形的判定和性质,全等三角形的判定与性质,解直角三角形等知识,解题的关键是学会添加常用辅助线,学会利用参数构建方程解决问题.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
浙江省中考数学考前冲刺每日一练26(精选全省各市历年经典真题,包含常考题型、易错题型、 小压轴、大压轴)
1.据中国宁波网消息:2023年一季度宁波全市实现地区生产总值380180000000元,同比增长4.5%.数380180000000用科学记数法表示为( )
A.0.38018×1012 B.3.8018×1011
C.3.8018×1010 D.38.018×1010
2.一个不透明的袋子里装有3个绿球、3个黑球和6个红球,它们除颜色外其余相同.从袋中任意摸出一个球为绿球的概率为 .
3.如图,在Rt△ABC中,∠C=90°,E为AB边上一点,以AE为直径的半圆O与BC相切于点D,连结AD,BE=3,BD=3.P是AB边上的动点,当△ADP为等腰三角形时,AP的长为 .
4.在4×4的方格纸中,请按下列要求画出格点三角形(顶点均在格点上).
(1)在图1中先画出一个以格点P为顶点的等腰三角形PAB,再画出该三角形向右平移2个单位后的△P′A′B′.
(2)将图2中的格点△ABC绕点C按顺时针方向旋转90°,画出经旋转后的△A′B′C.
5.如图1,锐角△ABC内接于⊙O,D为BC的中点,连结AD并延长交⊙O于点E,连结BE,CE,过C作AC的垂线交AE于点F,点G在AD上,连结BG,CG,若BC平分∠EBG且∠BCG=∠AFC.
(1)求∠BGC的度数.
(2)①求证:AF=BC.
②若AG=DF,求tan∠GBC的值.
(3)如图2,当点O恰好在BG上且OG=1时,求AC的长.
浙江省中考数学考前冲刺每日一练26(精选全省各市历年经典真题,包含常考题型、易错题型、 小压轴、大压轴)参考答案与试题解析
一.选择题(共1小题)
1.据中国宁波网消息:2023年一季度宁波全市实现地区生产总值380180000000元,同比增长4.5%.数380180000000用科学记数法表示为( )
A.0.38018×1012 B.3.8018×1011
C.3.8018×1010 D.38.018×1010
【分析】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值≥10时,n是正整数;当原数的绝对值<1时,n是负整数.
【解答】解:380180000000=3.8018×1011.
故选:B.
【点评】此题考查科学记数法的表示方法.科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数,表示时关键要正确确定a的值以及n的值.
二.填空题(共2小题)
2.一个不透明的袋子里装有3个绿球、3个黑球和6个红球,它们除颜色外其余相同.从袋中任意摸出一个球为绿球的概率为 .
【分析】根据概率公式可知,用绿球的个数除以球的总数即可.
【解答】解:∵袋子里装有3个绿球、3个黑球和6个红球,
∴从袋中任意摸出一个球是绿球的概率为.
故答案为:.
【点评】此题考查了概率公式,熟知概率=所求情况数与总情况数之比是解题的关键.
3.如图,在Rt△ABC中,∠C=90°,E为AB边上一点,以AE为直径的半圆O与BC相切于点D,连结AD,BE=3,BD=3.P是AB边上的动点,当△ADP为等腰三角形时,AP的长为 6或2 .
【分析】连接OD,DE,根据切线的性质和勾股定理求出OD=6,然后分三种情况讨论:①当AP=PD时,此时P与O重合,②如图2,当AP′=AD时,③如图3,当DP′′=AD时,分别进行求解即可.
【解答】解:如图1,连接OD,DE,
∵半圆O与BC相切于点D,
∴OD⊥BC,
在Rt△OBD中,OB=OE+BE=OD+3,BD=3.
∴OB2=BD2+OD2,
∴(OD+3)2=(3)2+OD2,
解得OD=6,
∴AO=EO=OD=6,
①当AP=PD时,此时P与O重合,
∴AP=AO=6;
②如图2,当AP′=AD时,
在Rt△ABC中,
∵∠C=90°,
∴AC⊥BC,
∴OD∥AC,
∴△BOD∽△BAC,
∴==,
∴==,
∴AC=10,CD=2,
∴AD===2,
∴AP′=AD=2;
③如图3,当DP′′=AD时,
∵AD=2,
∴DP′′=AD=2,
∵OD=OA,
∴∠ODA=∠BAD,
∴OD∥AC,
∴∠ODA=∠CAD,
∴∠BAD=∠CAD,
∴AD平分∠BAC,
过点D作DH⊥AE于点H,
∴AH=P″H,DH=DC=2,
∵AD=AD,
∴Rt△ADH≌Rt△ADC(HL),
∴AH=AC=10,
∴AH=AC=P″H=10,
∴AP″=2AH=20(P为AB边上一点,不符合题意,舍去),
综上所述:当△ADP为等腰三角形时,AP的长为6或2.
故答案为:6或2.
【点评】此题属于圆的综合题,考查了切线的性质,圆周角定理,勾股定理,相似三角形的判定与性质,全等三角形的判定与性质,等腰三角形的性质,综合性强,解决本题的关键是利用分类讨论思想.
三.解答题(共2小题)
4.在4×4的方格纸中,请按下列要求画出格点三角形(顶点均在格点上).
(1)在图1中先画出一个以格点P为顶点的等腰三角形PAB,再画出该三角形向右平移2个单位后的△P′A′B′.
(2)将图2中的格点△ABC绕点C按顺时针方向旋转90°,画出经旋转后的△A′B′C.
【分析】(1)根据等腰三角形的定义,平移变换的性质作出图形即可;
(2)根据旋转变换的性质作出图形即可.
【解答】解:(1)如图1,△P′A′B′即为所求;
(2)如图2,△A′B′C即为所求.
【点评】本题考查作图﹣旋转变换,平移变换,等腰三角形的性质等知识,解题的关键是理解题意,灵活运用所学知识解决问题.
5.如图1,锐角△ABC内接于⊙O,D为BC的中点,连结AD并延长交⊙O于点E,连结BE,CE,过C作AC的垂线交AE于点F,点G在AD上,连结BG,CG,若BC平分∠EBG且∠BCG=∠AFC.
(1)求∠BGC的度数.
(2)①求证:AF=BC.
②若AG=DF,求tan∠GBC的值.
(3)如图2,当点O恰好在BG上且OG=1时,求AC的长.
【分析】(1)根据同弧圆周角相等得∠EBC=∠EAC,然后利用直角三角形两个锐角互余即可解决问题;
(2)①证明△ACF≌△BGC(ASA),即可解决问题;
②过点C作CH⊥EG于点H,设AG=DF=2x,根据勾股定理和锐角三角函数即可解决问题;
(3)过点O作OM⊥BE于点M,连结OC交AE于点N,分别证明△EBD≌△NCD(ASA),△COG≌△OBM(AAS),得BM=OG=1,设OB=OC=r,然后由△GON∽△GBE,对应边成比例,求出r的值,进而可求AC的长.
【解答】(1)解:∵BC平分∠EBG,
∴∠EBC=∠CBG,
∵∠EBC=∠EAC,
∴∠CBG=∠EAC,
∵AC⊥FC,
∴∠AFC+∠EAC=90°,
∵∠BCG=∠AFC,
∴∠BCG+∠CBG=90°,
∴∠BGC=90°;
(2)①证明:∵∠BGC=90°,D为BC中点,
∴GD=CD,
∴∠DGC=∠DCG,
∵∠BCG=∠AFC,
∴∠DGC=∠AFC,
∴CF=CG,
∵∠ACF=∠BGC=90°,
∴△ACF≌△BGC(ASA),
∴AF=BC;
②解:如图1,过点C作CH⊥EG于点H,
设AG=DF=2x,
∵△ACF≌△BGC,
∴AF=BC=2DG,
∴CD=DG=AG+DF=4x,
∵CF=CG,
∴HG=HF=3x,
∴DH=x,AH=5x,
∴CH===x,
∴tan∠GBC=tan∠CAF==,
∴tan∠GBC的值为;
(3)解:如图2,过点O作OM⊥BE于点M,连结OC交AE于点N,
∵OB=OC,
∴∠CBE=∠OBC=∠OCB,
∴OC∥BE,
∵BD=CD,∠BDE=∠CDN,
∴△EBD≌△NCD(ASA),
∴BE=CN,
∵OC∥BE,
∴∠GOC=∠MBO,
∵∠CGO=∠OMB=90°,OC=OB,
∴△COG≌△OBM(AAS),
∴BM=OG=1,
∵OM⊥BE,
∴CN=BE=2BM=2,
设OB=OC=r,
∵OC∥BE,
∴△GON∽△GBE,
∴=,
∴=,
解得r=或r=(舍去),
由(2)知:△ACF≌△BGC,
∴AC=BG=BO+OG=r+1=.
∴AC的长为.
【点评】本题属于圆综合题,考查了垂径定理,圆周角定理,相似三角形的判定和性质,全等三角形的判定与性质,解直角三角形等知识,解题的关键是学会添加常用辅助线,学会利用参数构建方程解决问题.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
