浙江省中考数学考前冲刺每日一练28(精选全省各市历年经典真题,包含常考题型、易错题型、 小压轴、大压轴)
文档属性
| 名称 | 浙江省中考数学考前冲刺每日一练28(精选全省各市历年经典真题,包含常考题型、易错题型、 小压轴、大压轴) |  | |
| 格式 | doc | ||
| 文件大小 | 369.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-24 09:27:45 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
浙江省中考数学考前冲刺每日一练28(精选全省各市历年经典真题,包含常考题型、易错题型、 小压轴、大压轴)
1.分解因式:4a2﹣1=( )
A.(2a﹣1)(2a+1) B.(a﹣2)(a+2)
C.(a﹣4)(a+1) D.(4a﹣1)(a+1)
2.设二次函数y=a(x﹣m)(x﹣m﹣k)(a>0,m,k是实数),则( )
A.当k=2时,函数y的最小值为﹣a
B.当k=2时,函数y的最小值为﹣2a
C.当k=4时,函数y的最小值为﹣a
D.当k=4时,函数y的最小值为﹣2a
3.如图,平行四边形ABCD的对角线AC,BD相交于点O,点E,F在对角线BD上,且BE=EF=FD,连接AE,EC,CF,FA.
(1)求证:四边形AECF是平行四边形.
(2)若△ABE的面积等于2,求△CFO的面积.
4.设二次函数y=ax2+bx+1(a≠0,b是实数).已知函数值y和自变量x的部分对应取值如下表所示:
x … ﹣1 0 1 2 3 …
y … m 1 n 1 p …
(1)若m=4,
①求二次函数的表达式;
②写出一个符合条件的x的取值范围,使得y随x的增大而减小.
(2)若在m,n,p这三个实数中,只有一个是正数,求a的取值范围.
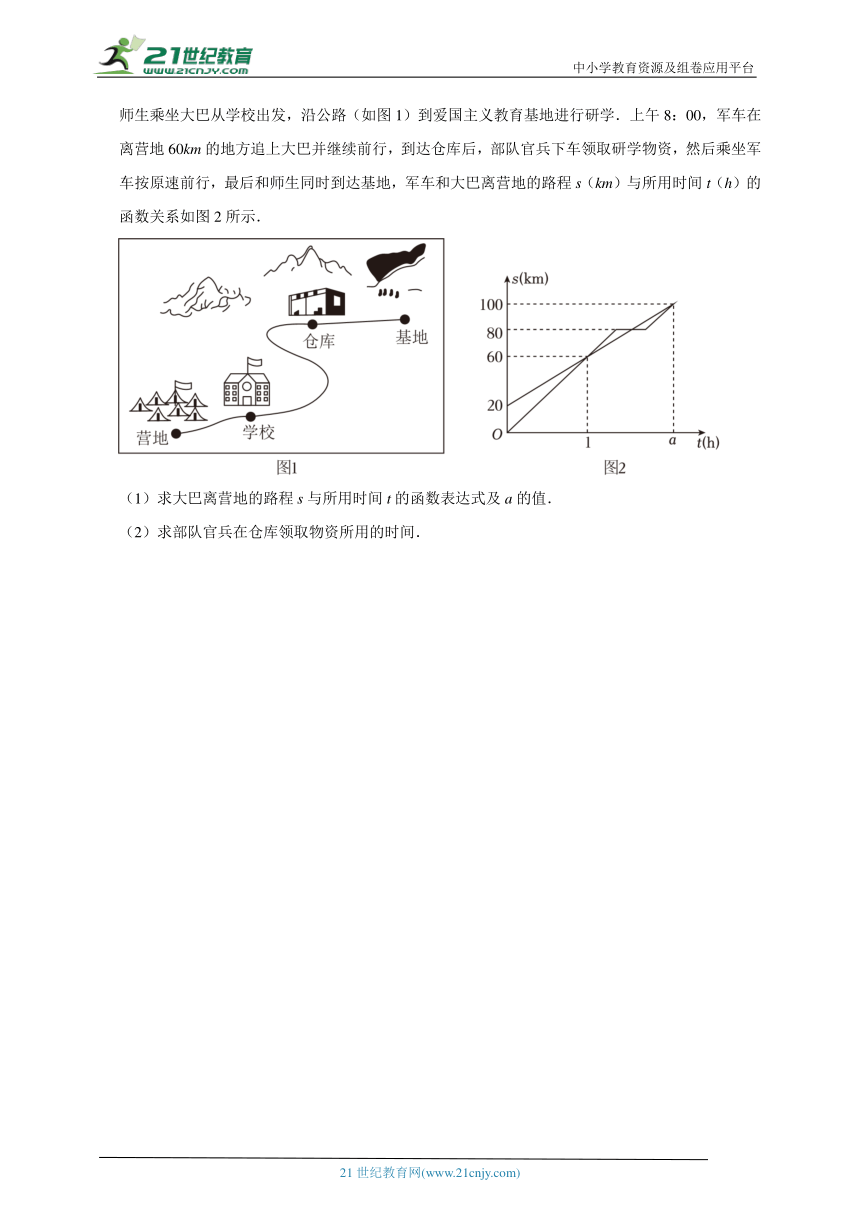
5.某校与部队联合开展红色之旅研学活动,上午7:00,部队官兵乘坐军车从营地出发,同时学校师生乘坐大巴从学校出发,沿公路(如图1)到爱国主义教育基地进行研学.上午8:00,军车在离营地60km的地方追上大巴并继续前行,到达仓库后,部队官兵下车领取研学物资,然后乘坐军车按原速前行,最后和师生同时到达基地,军车和大巴离营地的路程s(km)与所用时间t(h)的函数关系如图2所示.
(1)求大巴离营地的路程s与所用时间t的函数表达式及a的值.
(2)求部队官兵在仓库领取物资所用的时间.
浙江省中考数学考前冲刺每日一练28(精选全省各市历年经典真题,包含常考题型、易错题型、 小压轴、大压轴)参考答案与试题解析
一.选择题(共2小题)
1.分解因式:4a2﹣1=( )
A.(2a﹣1)(2a+1) B.(a﹣2)(a+2)
C.(a﹣4)(a+1) D.(4a﹣1)(a+1)
【分析】直接利用平方差公式分解因式得出答案.
【解答】解:4a2﹣1=(2a)2﹣12
=(2a﹣1)(2a+1).
故选:A.
【点评】此题主要考查了公式法分解因式,正确运用平方差公式分解因式是解题关键.
2.设二次函数y=a(x﹣m)(x﹣m﹣k)(a>0,m,k是实数),则( )
A.当k=2时,函数y的最小值为﹣a
B.当k=2时,函数y的最小值为﹣2a
C.当k=4时,函数y的最小值为﹣a
D.当k=4时,函数y的最小值为﹣2a
【分析】令y=0,求出二次函数与x轴的交点坐标,继而求出二次函数的对称轴,再代入二次函数解析式即可求出顶点的纵坐标,最后代入k的值进行判断即可.
【解答】解:令y=0,则(x﹣m)(x﹣m﹣k)=0,
∴x1=m,x2=m+k,
∴二次函数y=a(x﹣m)(x﹣m﹣k)与x轴的交点坐标是(m,0),(m+k,0),
∴二次函数的对称轴是:直线,
∵a>0,
∴y有最小值,
当时,y最小,
即,
当k=2时,函数y的最小值为;
当k=4时,函数y的最小值为,
故选:A.
【点评】本题考查了二次函数的最值问题,熟练掌握求二次函数的顶点坐标是解题的关键.
二.解答题(共3小题)
3.如图,平行四边形ABCD的对角线AC,BD相交于点O,点E,F在对角线BD上,且BE=EF=FD,连接AE,EC,CF,FA.
(1)求证:四边形AECF是平行四边形.
(2)若△ABE的面积等于2,求△CFO的面积.
【分析】(1)由平行四边形的性质得AO=CO,BO=DO,再证OE=OF,即可得出结论;
(2)由平行四边形的性质可求解.
【解答】(1)证明:∵四边形ABCD是平行四边形,
∴AO=CO,BO=DO,
∵BE=DF,
∴EO=FO,
∴四边形AECF是平行四边形;
(2)解:∵BE=EF,
∴S△ABE=S△AEF=2,
∵四边形AECF是平行四边形,
∴S△AEF=S△CEF=2,EO=FO,
∴△CFO的面积=1.
【点评】本题考查了平行四边形的判定和性质,三角形的面积公式,掌握平行四边形的性质是解题的关键.
4.设二次函数y=ax2+bx+1(a≠0,b是实数).已知函数值y和自变量x的部分对应取值如下表所示:
x … ﹣1 0 1 2 3 …
y … m 1 n 1 p …
(1)若m=4,
①求二次函数的表达式;
②写出一个符合条件的x的取值范围,使得y随x的增大而减小.
(2)若在m,n,p这三个实数中,只有一个是正数,求a的取值范围.
【分析】(1)①利用待定系数法即可求得;
②利用二次函数的性质得出结论;
(2)根据题意m≤0,由﹣=1,得出b=﹣2a,则二次函数为y=ax2﹣2ax+1,得出m=a+2a+1≤0,解得a≤﹣.
【解答】解:(1)①由题意得,
解得,
∴二次函数的表达式是y=x2﹣2x+1;
②∵y=x2﹣2x+1=(x﹣1)2,
∴抛物线开口向上,对称轴为直线x=1,
∴当x<1时,y随x的增大而减小;
(2)∵x=0和x=2时的函数值都是1,
∴抛物线的对称轴为直线x=﹣=1,
∴(1,n)是顶点,(﹣1,m)和(3,p)关于对称轴对称,
若在m,n,p这三个实数中,只有一个是正数,则抛物线必须开口向下,且m≤0,
∵﹣=1,
∴b=﹣2a,
∴二次函数为y=ax2﹣2ax+1,
∴m=a+2a+1≤0,
∴a≤﹣.
【点评】本题考查了二次函数的图象与系数的关系,待定系数法求二次函数的解析式,二次函数的性质,二次函数图象上点的坐标特征,能够明确题意得出m=a+2a+1<0是解题的关键.
5.某校与部队联合开展红色之旅研学活动,上午7:00,部队官兵乘坐军车从营地出发,同时学校师生乘坐大巴从学校出发,沿公路(如图1)到爱国主义教育基地进行研学.上午8:00,军车在离营地60km的地方追上大巴并继续前行,到达仓库后,部队官兵下车领取研学物资,然后乘坐军车按原速前行,最后和师生同时到达基地,军车和大巴离营地的路程s(km)与所用时间t(h)的函数关系如图2所示.
(1)求大巴离营地的路程s与所用时间t的函数表达式及a的值.
(2)求部队官兵在仓库领取物资所用的时间.
【分析】(1)求出大巴速度为=40(km/h),即得s=20+40t;令s=100得a=2;
(2)求出军车速度为60÷1=60(km/h),设部队官兵在仓库领取物资所用的时间为x h,可得:60(2﹣x)=100,即可解得答案.
【解答】解:(1)由函数图象可得,大巴速度为=40(km/h),
∴s=20+40t;
当s=100时,100=20+40t,
解得t=2,
∴a=2;
∴大巴离营地的路程s与所用时间t的函数表达式为s=20+40t,a的值为2;
(2)由函数图象可得,军车速度为60÷1=60(km/h),
设部队官兵在仓库领取物资所用的时间为x h,
根据题意得:60(2﹣x)=100,
解得:x=,
答:部队官兵在仓库领取物资所用的时间为h.
【点评】本题考查一次函数的应用,解题的关键是读懂题意,能从函数图象中获取有用的信息.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
浙江省中考数学考前冲刺每日一练28(精选全省各市历年经典真题,包含常考题型、易错题型、 小压轴、大压轴)
1.分解因式:4a2﹣1=( )
A.(2a﹣1)(2a+1) B.(a﹣2)(a+2)
C.(a﹣4)(a+1) D.(4a﹣1)(a+1)
2.设二次函数y=a(x﹣m)(x﹣m﹣k)(a>0,m,k是实数),则( )
A.当k=2时,函数y的最小值为﹣a
B.当k=2时,函数y的最小值为﹣2a
C.当k=4时,函数y的最小值为﹣a
D.当k=4时,函数y的最小值为﹣2a
3.如图,平行四边形ABCD的对角线AC,BD相交于点O,点E,F在对角线BD上,且BE=EF=FD,连接AE,EC,CF,FA.
(1)求证:四边形AECF是平行四边形.
(2)若△ABE的面积等于2,求△CFO的面积.
4.设二次函数y=ax2+bx+1(a≠0,b是实数).已知函数值y和自变量x的部分对应取值如下表所示:
x … ﹣1 0 1 2 3 …
y … m 1 n 1 p …
(1)若m=4,
①求二次函数的表达式;
②写出一个符合条件的x的取值范围,使得y随x的增大而减小.
(2)若在m,n,p这三个实数中,只有一个是正数,求a的取值范围.
5.某校与部队联合开展红色之旅研学活动,上午7:00,部队官兵乘坐军车从营地出发,同时学校师生乘坐大巴从学校出发,沿公路(如图1)到爱国主义教育基地进行研学.上午8:00,军车在离营地60km的地方追上大巴并继续前行,到达仓库后,部队官兵下车领取研学物资,然后乘坐军车按原速前行,最后和师生同时到达基地,军车和大巴离营地的路程s(km)与所用时间t(h)的函数关系如图2所示.
(1)求大巴离营地的路程s与所用时间t的函数表达式及a的值.
(2)求部队官兵在仓库领取物资所用的时间.
浙江省中考数学考前冲刺每日一练28(精选全省各市历年经典真题,包含常考题型、易错题型、 小压轴、大压轴)参考答案与试题解析
一.选择题(共2小题)
1.分解因式:4a2﹣1=( )
A.(2a﹣1)(2a+1) B.(a﹣2)(a+2)
C.(a﹣4)(a+1) D.(4a﹣1)(a+1)
【分析】直接利用平方差公式分解因式得出答案.
【解答】解:4a2﹣1=(2a)2﹣12
=(2a﹣1)(2a+1).
故选:A.
【点评】此题主要考查了公式法分解因式,正确运用平方差公式分解因式是解题关键.
2.设二次函数y=a(x﹣m)(x﹣m﹣k)(a>0,m,k是实数),则( )
A.当k=2时,函数y的最小值为﹣a
B.当k=2时,函数y的最小值为﹣2a
C.当k=4时,函数y的最小值为﹣a
D.当k=4时,函数y的最小值为﹣2a
【分析】令y=0,求出二次函数与x轴的交点坐标,继而求出二次函数的对称轴,再代入二次函数解析式即可求出顶点的纵坐标,最后代入k的值进行判断即可.
【解答】解:令y=0,则(x﹣m)(x﹣m﹣k)=0,
∴x1=m,x2=m+k,
∴二次函数y=a(x﹣m)(x﹣m﹣k)与x轴的交点坐标是(m,0),(m+k,0),
∴二次函数的对称轴是:直线,
∵a>0,
∴y有最小值,
当时,y最小,
即,
当k=2时,函数y的最小值为;
当k=4时,函数y的最小值为,
故选:A.
【点评】本题考查了二次函数的最值问题,熟练掌握求二次函数的顶点坐标是解题的关键.
二.解答题(共3小题)
3.如图,平行四边形ABCD的对角线AC,BD相交于点O,点E,F在对角线BD上,且BE=EF=FD,连接AE,EC,CF,FA.
(1)求证:四边形AECF是平行四边形.
(2)若△ABE的面积等于2,求△CFO的面积.
【分析】(1)由平行四边形的性质得AO=CO,BO=DO,再证OE=OF,即可得出结论;
(2)由平行四边形的性质可求解.
【解答】(1)证明:∵四边形ABCD是平行四边形,
∴AO=CO,BO=DO,
∵BE=DF,
∴EO=FO,
∴四边形AECF是平行四边形;
(2)解:∵BE=EF,
∴S△ABE=S△AEF=2,
∵四边形AECF是平行四边形,
∴S△AEF=S△CEF=2,EO=FO,
∴△CFO的面积=1.
【点评】本题考查了平行四边形的判定和性质,三角形的面积公式,掌握平行四边形的性质是解题的关键.
4.设二次函数y=ax2+bx+1(a≠0,b是实数).已知函数值y和自变量x的部分对应取值如下表所示:
x … ﹣1 0 1 2 3 …
y … m 1 n 1 p …
(1)若m=4,
①求二次函数的表达式;
②写出一个符合条件的x的取值范围,使得y随x的增大而减小.
(2)若在m,n,p这三个实数中,只有一个是正数,求a的取值范围.
【分析】(1)①利用待定系数法即可求得;
②利用二次函数的性质得出结论;
(2)根据题意m≤0,由﹣=1,得出b=﹣2a,则二次函数为y=ax2﹣2ax+1,得出m=a+2a+1≤0,解得a≤﹣.
【解答】解:(1)①由题意得,
解得,
∴二次函数的表达式是y=x2﹣2x+1;
②∵y=x2﹣2x+1=(x﹣1)2,
∴抛物线开口向上,对称轴为直线x=1,
∴当x<1时,y随x的增大而减小;
(2)∵x=0和x=2时的函数值都是1,
∴抛物线的对称轴为直线x=﹣=1,
∴(1,n)是顶点,(﹣1,m)和(3,p)关于对称轴对称,
若在m,n,p这三个实数中,只有一个是正数,则抛物线必须开口向下,且m≤0,
∵﹣=1,
∴b=﹣2a,
∴二次函数为y=ax2﹣2ax+1,
∴m=a+2a+1≤0,
∴a≤﹣.
【点评】本题考查了二次函数的图象与系数的关系,待定系数法求二次函数的解析式,二次函数的性质,二次函数图象上点的坐标特征,能够明确题意得出m=a+2a+1<0是解题的关键.
5.某校与部队联合开展红色之旅研学活动,上午7:00,部队官兵乘坐军车从营地出发,同时学校师生乘坐大巴从学校出发,沿公路(如图1)到爱国主义教育基地进行研学.上午8:00,军车在离营地60km的地方追上大巴并继续前行,到达仓库后,部队官兵下车领取研学物资,然后乘坐军车按原速前行,最后和师生同时到达基地,军车和大巴离营地的路程s(km)与所用时间t(h)的函数关系如图2所示.
(1)求大巴离营地的路程s与所用时间t的函数表达式及a的值.
(2)求部队官兵在仓库领取物资所用的时间.
【分析】(1)求出大巴速度为=40(km/h),即得s=20+40t;令s=100得a=2;
(2)求出军车速度为60÷1=60(km/h),设部队官兵在仓库领取物资所用的时间为x h,可得:60(2﹣x)=100,即可解得答案.
【解答】解:(1)由函数图象可得,大巴速度为=40(km/h),
∴s=20+40t;
当s=100时,100=20+40t,
解得t=2,
∴a=2;
∴大巴离营地的路程s与所用时间t的函数表达式为s=20+40t,a的值为2;
(2)由函数图象可得,军车速度为60÷1=60(km/h),
设部队官兵在仓库领取物资所用的时间为x h,
根据题意得:60(2﹣x)=100,
解得:x=,
答:部队官兵在仓库领取物资所用的时间为h.
【点评】本题考查一次函数的应用,解题的关键是读懂题意,能从函数图象中获取有用的信息.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
