浙江省中考数学考前冲刺每日一练29(精选全省各市历年经典真题,包含常考题型、易错题型、 小压轴、大压轴)
文档属性
| 名称 | 浙江省中考数学考前冲刺每日一练29(精选全省各市历年经典真题,包含常考题型、易错题型、 小压轴、大压轴) |  | |
| 格式 | doc | ||
| 文件大小 | 447.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-24 09:27:45 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
浙江省中考数学考前冲刺每日一练29(精选全省各市历年经典真题,包含常考题型、易错题型、 小压轴、大压轴)
1.某校要从四名学生中选拔一名参加市“汉字听写”大赛,将多轮选拔赛的成绩数据进行分析得到每名学生的平均成绩及其方差如表所示:根据表中数据,可以判断同学甲是这四名选手中成绩最好且发挥最稳定的学生,则m,n的值可以是( )
甲 乙 两 丁
平均数(单位:分) m 90 91 88
方差s2(单位:分2) n 12.5 14.5 11
A.m=92,n=15 B.m=92,n=8.5
C.m=85,n=10 D.m=90,n=12.5
2.《九章算术》是中国古代的一本重要数学著作,其中有一道方程的应用题:“五只雀、六只燕,共重16两,雀重燕轻.互换其中一只,恰好一样重.问每只雀、燕的重量各为多少?”解:设雀每只x两,燕每只y两,则可列出方程组为( )
A. B. C. D.
3.将抛物线y=x2+4x+3向右平移n(n>0)个单位得到一条新抛物线,若点A(2,y1),B(4,y2) 在新抛物线上,且y1>y2,则n的值可以是( )
A.3 B.4 C.5 D.6
4.图①.图②、图③都是6×6的正方形网格,每个小正方形的边长均为1.每个小正方形的顶点叫做格点,故段AB的端点都在格点上.在给定的网格中,只用无刻度的直尺,按下列要求画图,只保留作图痕迹,不要求写画法.
(1)在图①中画△ABC,使△ABC的面积是10;
(2)在图②中画四边形ABDE,使四边形ABDE是轴对称图形;
(3)在图③中的线段AB上找一点P,使AP=2BP.
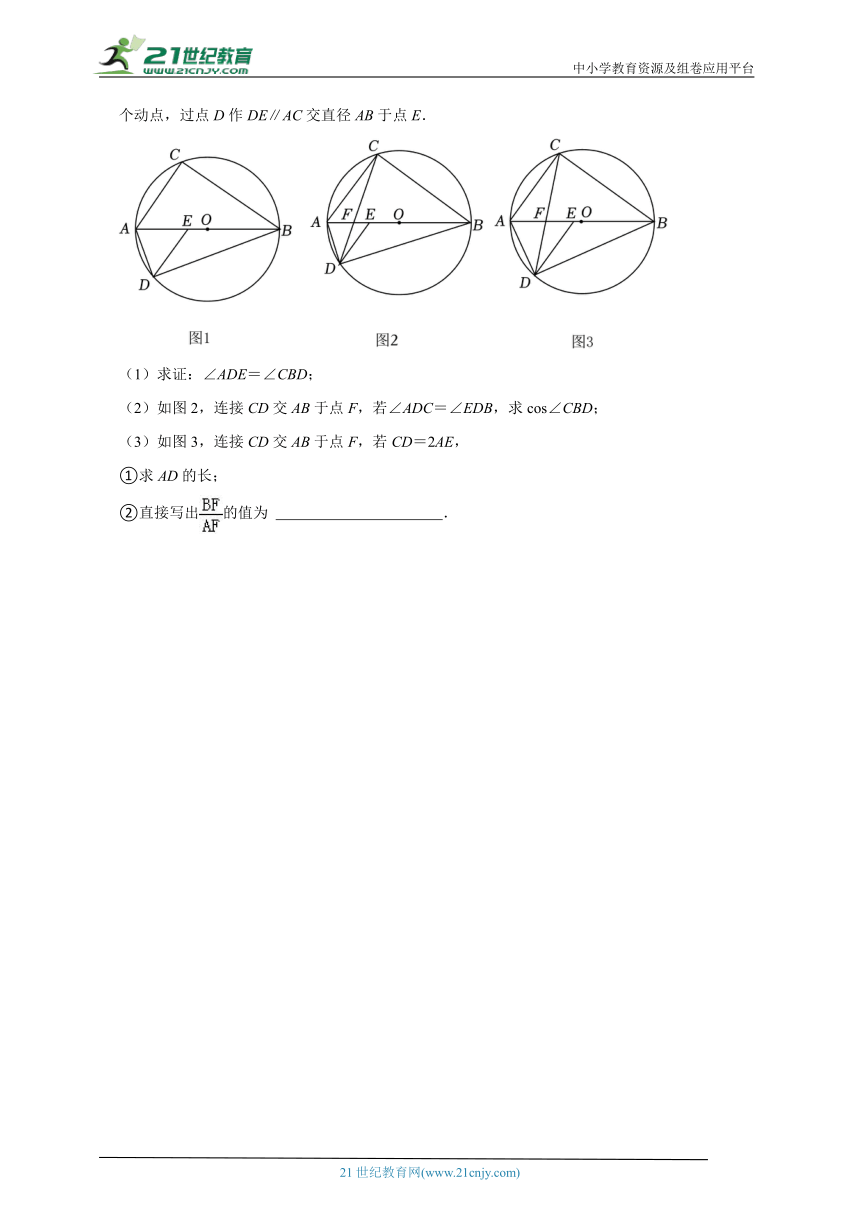
5.如图1,已知△ABC内接于⊙O,AB为⊙O的直径,AB=5,,点D是半圆上的一个动点,过点D作DE∥AC交直径AB于点E.
(1)求证:∠ADE=∠CBD;
(2)如图2,连接CD交AB于点F,若∠ADC=∠EDB,求cos∠CBD;
(3)如图3,连接CD交AB于点F,若CD=2AE,
①求AD的长;
②直接写出的值为 .
浙江省中考数学考前冲刺每日一练29(精选全省各市历年经典真题,包含常考题型、易错题型、 小压轴、大压轴)参考答案与试题解析
一.选择题(共3小题)
1.某校要从四名学生中选拔一名参加市“汉字听写”大赛,将多轮选拔赛的成绩数据进行分析得到每名学生的平均成绩及其方差如表所示:根据表中数据,可以判断同学甲是这四名选手中成绩最好且发挥最稳定的学生,则m,n的值可以是( )
甲 乙 两 丁
平均数(单位:分) m 90 91 88
方差s2(单位:分2) n 12.5 14.5 11
A.m=92,n=15 B.m=92,n=8.5
C.m=85,n=10 D.m=90,n=12.5
【分析】根据平均数和方差的意义求解即可.
【解答】解:∵甲是这四名选手中成绩最好的,
∴m>91,
又∵甲是发挥最稳定的学生,
∴n<11,
符合此条件的是m=92,n=8.5,
故选:B.
【点评】本题主要考查方差,解题的关键是掌握方差和平均数的意义.
2.《九章算术》是中国古代的一本重要数学著作,其中有一道方程的应用题:“五只雀、六只燕,共重16两,雀重燕轻.互换其中一只,恰好一样重.问每只雀、燕的重量各为多少?”解:设雀每只x两,燕每只y两,则可列出方程组为( )
A. B.
C. D.
【分析】直接利用“五只雀、六只燕,共重16两、互换其中一只,恰好一样重”,进而分别得出等式求出答案.
【解答】解:设雀每只x两,燕每只y两,则可列出方程组为:
.
故选:B.
【点评】此题主要考查了由实际问题抽象出二元一次方程组,正确表示出“互换一只恰好一样重”的等式是解题关键.
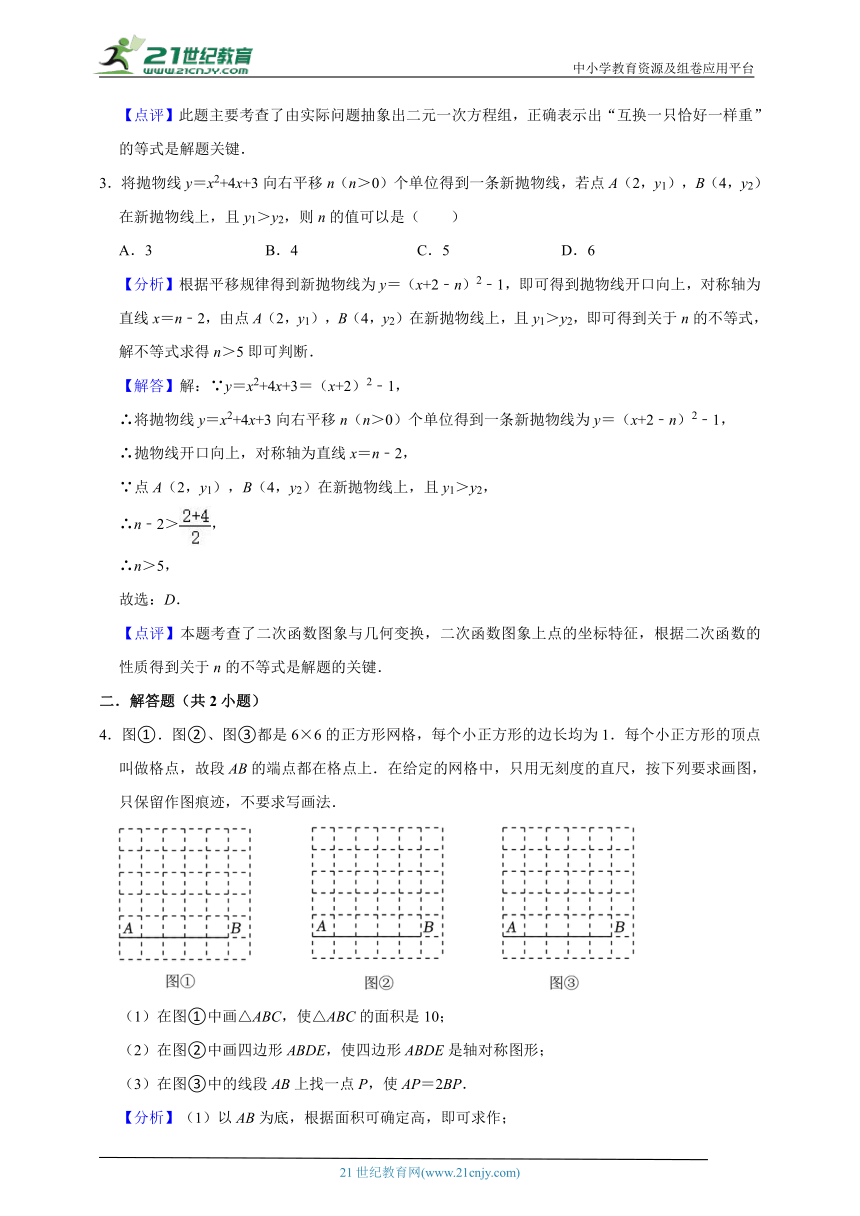
3.将抛物线y=x2+4x+3向右平移n(n>0)个单位得到一条新抛物线,若点A(2,y1),B(4,y2) 在新抛物线上,且y1>y2,则n的值可以是( )
A.3 B.4 C.5 D.6
【分析】根据平移规律得到新抛物线为y=(x+2﹣n)2﹣1,即可得到抛物线开口向上,对称轴为直线x=n﹣2,由点A(2,y1),B(4,y2)在新抛物线上,且y1>y2,即可得到关于n的不等式,解不等式求得n>5即可判断.
【解答】解:∵y=x2+4x+3=(x+2)2﹣1,
∴将抛物线y=x2+4x+3向右平移n(n>0)个单位得到一条新抛物线为y=(x+2﹣n)2﹣1,
∴抛物线开口向上,对称轴为直线x=n﹣2,
∵点A(2,y1),B(4,y2)在新抛物线上,且y1>y2,
∴n﹣2>,
∴n>5,
故选:D.
【点评】本题考查了二次函数图象与几何变换,二次函数图象上点的坐标特征,根据二次函数的性质得到关于n的不等式是解题的关键.
二.解答题(共2小题)
4.图①.图②、图③都是6×6的正方形网格,每个小正方形的边长均为1.每个小正方形的顶点叫做格点,故段AB的端点都在格点上.在给定的网格中,只用无刻度的直尺,按下列要求画图,只保留作图痕迹,不要求写画法.
(1)在图①中画△ABC,使△ABC的面积是10;
(2)在图②中画四边形ABDE,使四边形ABDE是轴对称图形;
(3)在图③中的线段AB上找一点P,使AP=2BP.
【分析】(1)以AB为底,根据面积可确定高,即可求作;
(2)以AB为一边,作出矩形即可;
(3)取AM=2,BN=1,连接MN交AB于P,即可求作.
【解答】解:(1)如图,△ABC为所求作(答案不唯一).
(2)如图,矩形ABDE为所求作(答案不唯一).
(3)如图,取AM=2,BN=1,
连接MN交AB于P,
∵△AMP∽△BNP,
∴,
∴AP=2BP,
∴P点为所求作.
【点评】本题考查了作图﹣轴对称变换,掌握图形特征,找出作法是解题的关键.
5.如图1,已知△ABC内接于⊙O,AB为⊙O的直径,AB=5,,点D是半圆上的一个动点,过点D作DE∥AC交直径AB于点E.
(1)求证:∠ADE=∠CBD;
(2)如图2,连接CD交AB于点F,若∠ADC=∠EDB,求cos∠CBD;
(3)如图3,连接CD交AB于点F,若CD=2AE,
①求AD的长;
②直接写出的值为 .
【分析】(1)延长DE交⊙O于点P,根据平行弦的性质得出,进而得出,进而即可求解;
(2)延长DE交⊙O于点P,根据AB为⊙O的直径,AB=5,,得出AC=3,BC=4,进而根据弧的关系,证明∠CBD=∠ACB,即可求解;
(3)①证明△BCD∽△DAE,即可求解;
②勾股定理求得BD,证明△DAF∽△BCF,得出BF=2DF,证明△ACF∽△DBF,求得BF,进而求得AF,即可求解.
【解答】(1)证明:如图所示,延长DE交⊙O于点P,
∵DE∥AC,
∴,
∴,
∴∠ADE=∠CBD;
(2)解:如图所示,延长DF交⊙O于点P,
∵AB为⊙O的直径,AB=5,,
∴∠ACB=90°,设AC=3k,BC=4k,则AB=5k,
∴k=1,
∴AC=3,BC=4,
∵∠ADC=∠EDB,
∴,
∴,
∴PB=AC=3,AP=BC=4,
∵,
∴∠ABD=∠CBP,
∴∠CBD=∠ABC+∠CBP=∠ABP,
∵,
∴∠ABP=∠CAB,
∴∠CBD=∠CAB,
∴;
(3)解:①由(1)可知∠ADE=∠CBD,
∵,
∴∠DAE=∠DCB,
∴△BCD∽△DAE,
∴,
∵CD=2AE,
∴BC=2AD,
∵BC=4,
∴AD=2;
②∵AD=2,
∴,
∵,
∴∠DAF=∠DCB,
∵,
∴∠ADF=∠ABC,
∴△DAF∽△BCF,
∴,
∴BF=2DF,
∵∠ACD=∠ABD,∠CAB=∠CDB,
∴△ACF∽△DBF,
∴,
∴,
解得:BF=,
∴AF=,
∴=,
故答案为:.
【点评】本题考查了圆的综合应用,掌握垂径定理平行弦问题,同弧所对的圆周角相等,直径所对的圆周角是直角,已知正切求边长,求余弦,相似三角形的性质与判定是解题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
浙江省中考数学考前冲刺每日一练29(精选全省各市历年经典真题,包含常考题型、易错题型、 小压轴、大压轴)
1.某校要从四名学生中选拔一名参加市“汉字听写”大赛,将多轮选拔赛的成绩数据进行分析得到每名学生的平均成绩及其方差如表所示:根据表中数据,可以判断同学甲是这四名选手中成绩最好且发挥最稳定的学生,则m,n的值可以是( )
甲 乙 两 丁
平均数(单位:分) m 90 91 88
方差s2(单位:分2) n 12.5 14.5 11
A.m=92,n=15 B.m=92,n=8.5
C.m=85,n=10 D.m=90,n=12.5
2.《九章算术》是中国古代的一本重要数学著作,其中有一道方程的应用题:“五只雀、六只燕,共重16两,雀重燕轻.互换其中一只,恰好一样重.问每只雀、燕的重量各为多少?”解:设雀每只x两,燕每只y两,则可列出方程组为( )
A. B. C. D.
3.将抛物线y=x2+4x+3向右平移n(n>0)个单位得到一条新抛物线,若点A(2,y1),B(4,y2) 在新抛物线上,且y1>y2,则n的值可以是( )
A.3 B.4 C.5 D.6
4.图①.图②、图③都是6×6的正方形网格,每个小正方形的边长均为1.每个小正方形的顶点叫做格点,故段AB的端点都在格点上.在给定的网格中,只用无刻度的直尺,按下列要求画图,只保留作图痕迹,不要求写画法.
(1)在图①中画△ABC,使△ABC的面积是10;
(2)在图②中画四边形ABDE,使四边形ABDE是轴对称图形;
(3)在图③中的线段AB上找一点P,使AP=2BP.
5.如图1,已知△ABC内接于⊙O,AB为⊙O的直径,AB=5,,点D是半圆上的一个动点,过点D作DE∥AC交直径AB于点E.
(1)求证:∠ADE=∠CBD;
(2)如图2,连接CD交AB于点F,若∠ADC=∠EDB,求cos∠CBD;
(3)如图3,连接CD交AB于点F,若CD=2AE,
①求AD的长;
②直接写出的值为 .
浙江省中考数学考前冲刺每日一练29(精选全省各市历年经典真题,包含常考题型、易错题型、 小压轴、大压轴)参考答案与试题解析
一.选择题(共3小题)
1.某校要从四名学生中选拔一名参加市“汉字听写”大赛,将多轮选拔赛的成绩数据进行分析得到每名学生的平均成绩及其方差如表所示:根据表中数据,可以判断同学甲是这四名选手中成绩最好且发挥最稳定的学生,则m,n的值可以是( )
甲 乙 两 丁
平均数(单位:分) m 90 91 88
方差s2(单位:分2) n 12.5 14.5 11
A.m=92,n=15 B.m=92,n=8.5
C.m=85,n=10 D.m=90,n=12.5
【分析】根据平均数和方差的意义求解即可.
【解答】解:∵甲是这四名选手中成绩最好的,
∴m>91,
又∵甲是发挥最稳定的学生,
∴n<11,
符合此条件的是m=92,n=8.5,
故选:B.
【点评】本题主要考查方差,解题的关键是掌握方差和平均数的意义.
2.《九章算术》是中国古代的一本重要数学著作,其中有一道方程的应用题:“五只雀、六只燕,共重16两,雀重燕轻.互换其中一只,恰好一样重.问每只雀、燕的重量各为多少?”解:设雀每只x两,燕每只y两,则可列出方程组为( )
A. B.
C. D.
【分析】直接利用“五只雀、六只燕,共重16两、互换其中一只,恰好一样重”,进而分别得出等式求出答案.
【解答】解:设雀每只x两,燕每只y两,则可列出方程组为:
.
故选:B.
【点评】此题主要考查了由实际问题抽象出二元一次方程组,正确表示出“互换一只恰好一样重”的等式是解题关键.
3.将抛物线y=x2+4x+3向右平移n(n>0)个单位得到一条新抛物线,若点A(2,y1),B(4,y2) 在新抛物线上,且y1>y2,则n的值可以是( )
A.3 B.4 C.5 D.6
【分析】根据平移规律得到新抛物线为y=(x+2﹣n)2﹣1,即可得到抛物线开口向上,对称轴为直线x=n﹣2,由点A(2,y1),B(4,y2)在新抛物线上,且y1>y2,即可得到关于n的不等式,解不等式求得n>5即可判断.
【解答】解:∵y=x2+4x+3=(x+2)2﹣1,
∴将抛物线y=x2+4x+3向右平移n(n>0)个单位得到一条新抛物线为y=(x+2﹣n)2﹣1,
∴抛物线开口向上,对称轴为直线x=n﹣2,
∵点A(2,y1),B(4,y2)在新抛物线上,且y1>y2,
∴n﹣2>,
∴n>5,
故选:D.
【点评】本题考查了二次函数图象与几何变换,二次函数图象上点的坐标特征,根据二次函数的性质得到关于n的不等式是解题的关键.
二.解答题(共2小题)
4.图①.图②、图③都是6×6的正方形网格,每个小正方形的边长均为1.每个小正方形的顶点叫做格点,故段AB的端点都在格点上.在给定的网格中,只用无刻度的直尺,按下列要求画图,只保留作图痕迹,不要求写画法.
(1)在图①中画△ABC,使△ABC的面积是10;
(2)在图②中画四边形ABDE,使四边形ABDE是轴对称图形;
(3)在图③中的线段AB上找一点P,使AP=2BP.
【分析】(1)以AB为底,根据面积可确定高,即可求作;
(2)以AB为一边,作出矩形即可;
(3)取AM=2,BN=1,连接MN交AB于P,即可求作.
【解答】解:(1)如图,△ABC为所求作(答案不唯一).
(2)如图,矩形ABDE为所求作(答案不唯一).
(3)如图,取AM=2,BN=1,
连接MN交AB于P,
∵△AMP∽△BNP,
∴,
∴AP=2BP,
∴P点为所求作.
【点评】本题考查了作图﹣轴对称变换,掌握图形特征,找出作法是解题的关键.
5.如图1,已知△ABC内接于⊙O,AB为⊙O的直径,AB=5,,点D是半圆上的一个动点,过点D作DE∥AC交直径AB于点E.
(1)求证:∠ADE=∠CBD;
(2)如图2,连接CD交AB于点F,若∠ADC=∠EDB,求cos∠CBD;
(3)如图3,连接CD交AB于点F,若CD=2AE,
①求AD的长;
②直接写出的值为 .
【分析】(1)延长DE交⊙O于点P,根据平行弦的性质得出,进而得出,进而即可求解;
(2)延长DE交⊙O于点P,根据AB为⊙O的直径,AB=5,,得出AC=3,BC=4,进而根据弧的关系,证明∠CBD=∠ACB,即可求解;
(3)①证明△BCD∽△DAE,即可求解;
②勾股定理求得BD,证明△DAF∽△BCF,得出BF=2DF,证明△ACF∽△DBF,求得BF,进而求得AF,即可求解.
【解答】(1)证明:如图所示,延长DE交⊙O于点P,
∵DE∥AC,
∴,
∴,
∴∠ADE=∠CBD;
(2)解:如图所示,延长DF交⊙O于点P,
∵AB为⊙O的直径,AB=5,,
∴∠ACB=90°,设AC=3k,BC=4k,则AB=5k,
∴k=1,
∴AC=3,BC=4,
∵∠ADC=∠EDB,
∴,
∴,
∴PB=AC=3,AP=BC=4,
∵,
∴∠ABD=∠CBP,
∴∠CBD=∠ABC+∠CBP=∠ABP,
∵,
∴∠ABP=∠CAB,
∴∠CBD=∠CAB,
∴;
(3)解:①由(1)可知∠ADE=∠CBD,
∵,
∴∠DAE=∠DCB,
∴△BCD∽△DAE,
∴,
∵CD=2AE,
∴BC=2AD,
∵BC=4,
∴AD=2;
②∵AD=2,
∴,
∵,
∴∠DAF=∠DCB,
∵,
∴∠ADF=∠ABC,
∴△DAF∽△BCF,
∴,
∴BF=2DF,
∵∠ACD=∠ABD,∠CAB=∠CDB,
∴△ACF∽△DBF,
∴,
∴,
解得:BF=,
∴AF=,
∴=,
故答案为:.
【点评】本题考查了圆的综合应用,掌握垂径定理平行弦问题,同弧所对的圆周角相等,直径所对的圆周角是直角,已知正切求边长,求余弦,相似三角形的性质与判定是解题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
