浙江省中考数学考前冲刺每日一练30(精选全省各市历年经典真题,包含常考题型、易错题型、 小压轴、大压轴)
文档属性
| 名称 | 浙江省中考数学考前冲刺每日一练30(精选全省各市历年经典真题,包含常考题型、易错题型、 小压轴、大压轴) |  | |
| 格式 | doc | ||
| 文件大小 | 447.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-24 09:27:45 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
浙江省中考数学考前冲刺每日一练30(精选全省各市历年经典真题,包含常考题型、易错题型、 小压轴、大压轴)
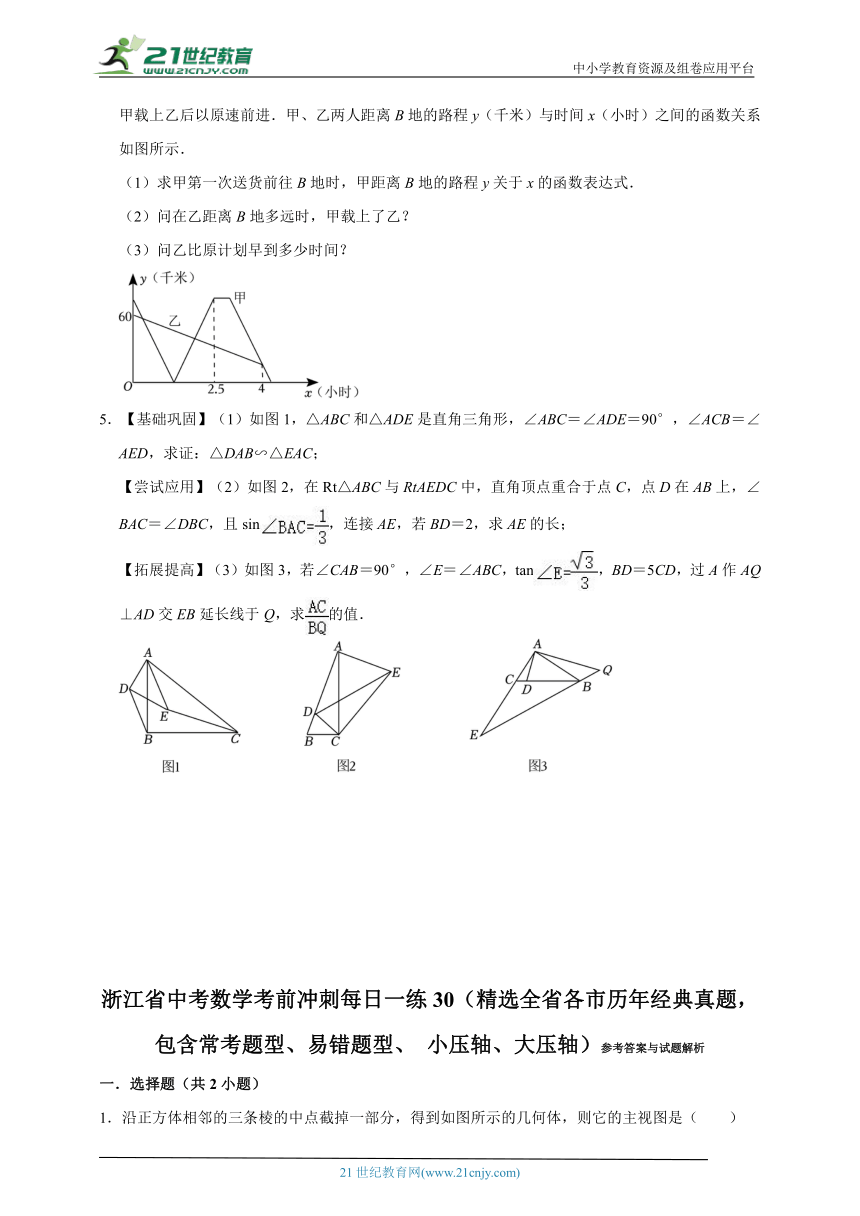
1.沿正方体相邻的三条棱的中点截掉一部分,得到如图所示的几何体,则它的主视图是( )
A. B. C. D.
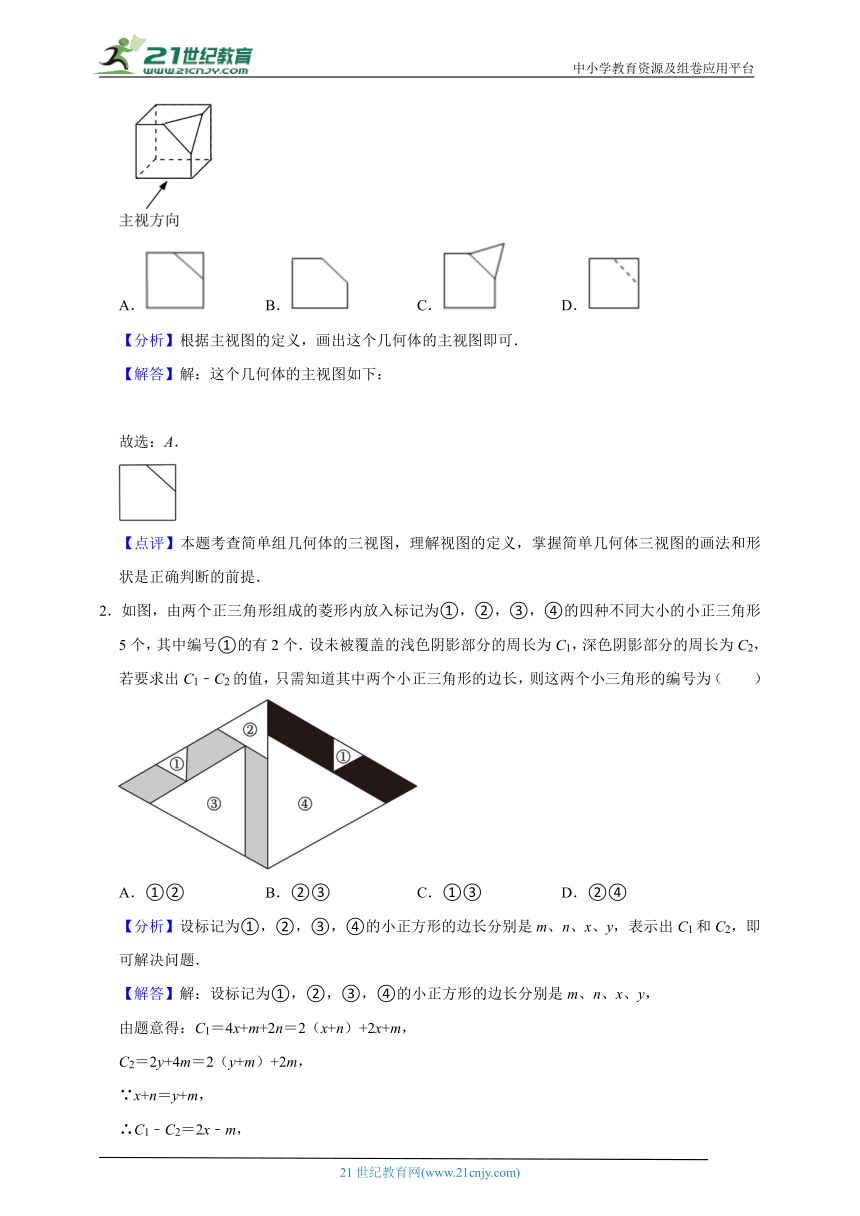
2.如图,由两个正三角形组成的菱形内放入标记为①,②,③,④的四种不同大小的小正三角形5个,其中编号①的有2个.设未被覆盖的浅色阴影部分的周长为C1,深色阴影部分的周长为C2,若要求出C1﹣C2的值,只需知道其中两个小正三角形的边长,则这两个小三角形的编号为( )
A.①② B.②③ C.①③ D.②④
3.如图所示的电路图,同时闭合两个开关能使小灯泡发亮的概率是 .
4.甲开车从A地前往B地送货,同时,乙从C地出发骑车前往B地,C在A,B两地之间且距离A地15千米.甲到达B地后以相同的速度立马返回A地,在A地休息半小时后,又以相同的速度前往B地送第二批货,乙出发后4小时遇上送货的甲,乙让甲捎上自己(上下车时间忽略不计),甲载上乙后以原速前进.甲、乙两人距离B地的路程y(千米)与时间x(小时)之间的函数关系如图所示.
(1)求甲第一次送货前往B地时,甲距离B地的路程y关于x的函数表达式.
(2)问在乙距离B地多远时,甲载上了乙?
(3)问乙比原计划早到多少时间?
5.【基础巩固】(1)如图1,△ABC和△ADE是直角三角形,∠ABC=∠ADE=90°,∠ACB=∠AED,求证:△DAB∽△EAC;
【尝试应用】(2)如图2,在Rt△ABC与RtAEDC中,直角顶点重合于点C,点D在AB上,∠BAC=∠DBC,且sin,连接AE,若BD=2,求AE的长;
【拓展提高】(3)如图3,若∠CAB=90°,∠E=∠ABC,tan,BD=5CD,过A作AQ⊥AD交EB延长线于Q,求的值.
浙江省中考数学考前冲刺每日一练30(精选全省各市历年经典真题,包含常考题型、易错题型、 小压轴、大压轴)参考答案与试题解析
一.选择题(共2小题)
1.沿正方体相邻的三条棱的中点截掉一部分,得到如图所示的几何体,则它的主视图是( )
A. B. C. D.
【分析】根据主视图的定义,画出这个几何体的主视图即可.
【解答】解:这个几何体的主视图如下:
故选:A.
【点评】本题考查简单组几何体的三视图,理解视图的定义,掌握简单几何体三视图的画法和形状是正确判断的前提.
2.如图,由两个正三角形组成的菱形内放入标记为①,②,③,④的四种不同大小的小正三角形5个,其中编号①的有2个.设未被覆盖的浅色阴影部分的周长为C1,深色阴影部分的周长为C2,若要求出C1﹣C2的值,只需知道其中两个小正三角形的边长,则这两个小三角形的编号为( )
A.①② B.②③ C.①③ D.②④
【分析】设标记为①,②,③,④的小正方形的边长分别是m、n、x、y,表示出C1和C2,即可解决问题.
【解答】解:设标记为①,②,③,④的小正方形的边长分别是m、n、x、y,
由题意得:C1=4x+m+2n=2(x+n)+2x+m,
C2=2y+4m=2(y+m)+2m,
∵x+n=y+m,
∴C1﹣C2=2x﹣m,
∴只需知道编号是①③的两个小正三角形的边长,即可求出C1﹣C2的值.
故选:C.
【点评】本题考查菱形的性质,等边三角形的性质,关键是由菱形、等边三角形的性质,用m、n、x、y表示出C1和C2.
二.填空题(共1小题)
3.如图所示的电路图,同时闭合两个开关能使小灯泡发亮的概率是 .
【分析】画树状图,共有6种等可能的结果,其中能使灯泡发光的结果有4种,再由概率公式求解即可.
【解答】解:把开关S1、S2、S3分别记为1、2、3,
画树状图如下:
共有6种等可能的结果,其中能使灯泡发光的结果有4种,
∴同时闭合两个开关能使小灯泡发亮的概率是=,
故答案为:.
【点评】此题考查的是用树状图法求概率.树状图法可以不重复不遗漏的列出所有可能的结果,适合两步或两步以上完成的事件.用到的知识点为:概率=所求情况数与总情况数之比.
三.解答题(共2小题)
4.甲开车从A地前往B地送货,同时,乙从C地出发骑车前往B地,C在A,B两地之间且距离A地15千米.甲到达B地后以相同的速度立马返回A地,在A地休息半小时后,又以相同的速度前往B地送第二批货,乙出发后4小时遇上送货的甲,乙让甲捎上自己(上下车时间忽略不计),甲载上乙后以原速前进.甲、乙两人距离B地的路程y(千米)与时间x(小时)之间的函数关系如图所示.
(1)求甲第一次送货前往B地时,甲距离B地的路程y关于x的函数表达式.
(2)问在乙距离B地多远时,甲载上了乙?
(3)问乙比原计划早到多少时间?
【分析】(1)根据题意题意得出甲第一次送货去B地的函数图象经过(0,75),(1.25,0),然后用待定系数法求出函数解析式;
(2)根据甲送货的速度不变,求出第二次送货的解析式,再把x=4代入解析式求y即可;
(3)求出甲第二次到B地的时间,和乙按原计划到B地的时间作差即可.
【解答】解:(1)由题意得,A、B两地间的路程为60+15=75千米,
甲第一次到达B地用时2.5÷2=1.25小时.
∴甲第一次送货去B地的函数图象经过(0,75),(1.25,0),
设甲第一次送货去B地的函数表达式为y=kx+b(k≠0),
把(0,75),(1.25,0)代入解析式得:
,
解得,
∴y关于x的函数表达式为y=﹣60x+75(0≤x≤1.25);
(2)甲第二次送货的函数图象经过(3,75),
∵甲送货的速度不变,
∴设甲第二次送货的函数表达式为y=﹣60x+m.
把(3,75)代入y=﹣60x+m,得75=﹣60×3+m,
解得m=255,
∴甲第二次送货的函数表达式为y=﹣60x+255,
当x=4时,y=15,
答:在乙距离B地15km时,甲载上了乙;
(3)把y=0代入y=﹣60x+255,
得0=﹣60x+255,
解得,
∵乙的图象经过点(0,60),
∴设乙的函数表达式为y=nx+60,
把(4,15)代入y=nx+60,
得15=4x+60,
解得.
∴乙比原计划早到时间为(小时).
答:乙比原计划早到小时.
【点评】本题考查一次函数和一元一次方程的应用,关键是找到等量关系列出函数解析式.
5.【基础巩固】(1)如图1,△ABC和△ADE是直角三角形,∠ABC=∠ADE=90°,∠ACB=∠AED,求证:△DAB∽△EAC;
【尝试应用】(2)如图2,在Rt△ABC与RtAEDC中,直角顶点重合于点C,点D在AB上,∠BAC=∠DBC,且sin,连接AE,若BD=2,求AE的长;
【拓展提高】(3)如图3,若∠CAB=90°,∠E=∠ABC,tan,BD=5CD,过A作AQ⊥AD交EB延长线于Q,求的值.
【分析】(1)通过证明△ABC∽△ADE,可得,∠BAC=∠DAE,可得结论;
(2)通过证明△CBD∽△CAE,可得,即可求解;
(3)由锐角三角函数可求∠E=30°,由直角三角形的性质可求BC=2AC=6a,AB=AC=3a,通过证明∠DAH∽△QAB,可求BQ的长,即可求解.
【解答】(1)证明:∵∠ABC=∠ADE=90°,∠ACB=∠AED,
∴△ABC∽△ADE,
∴,∠BAC=∠DAE,
∴∠CAE=∠BAD,
∴△DAB∽△EAC;
(2)解:∵∠BAC=∠DBC,sin,
∴sin∠BAC=sin∠DBC==,
∴AB=3BC,DE=3CD,
∴AC==2BC,CE==2CD,
∴=2,
∵∠ACB=∠DCE=90°,
∴∠BCD=∠ACE,
∴△CBD∽△CAE,
∴,
∵BD=2,
∴AE=4;
(3)解:如图3,在AC上截取CH=CD,连接DH,
∵tanE=,
∴∠E=30°,
∴∠E=∠ABC=30°,∠ABE=60°,
设AC=3a,则BC=2AC=6a,AB=AC=3a,
∵BD=5CD,
∴BD=5a,CD=a=CH,
∵∠ACB=90°﹣∠ABC=60°,
∴△CDH是等边三角形,
∴CH=CD=HD=a,∠CHD=120°,
∴AH=2a,
∵∠ABQ=180°﹣∠ABE=120°,
∴∠ABQ=∠AHD,
∵∠BAC=∠DAQ=90°,
∴∠DAH∽△QAB,
∴,
∴=,
∴BQ=a,
∴=.
【点评】本题是相似形综合题,考查了等边三角形的判定和性质,相似三角形的判定和性质,直角三角形的性质等知识,添加恰当辅助线构造相似三角形是解题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
浙江省中考数学考前冲刺每日一练30(精选全省各市历年经典真题,包含常考题型、易错题型、 小压轴、大压轴)
1.沿正方体相邻的三条棱的中点截掉一部分,得到如图所示的几何体,则它的主视图是( )
A. B. C. D.
2.如图,由两个正三角形组成的菱形内放入标记为①,②,③,④的四种不同大小的小正三角形5个,其中编号①的有2个.设未被覆盖的浅色阴影部分的周长为C1,深色阴影部分的周长为C2,若要求出C1﹣C2的值,只需知道其中两个小正三角形的边长,则这两个小三角形的编号为( )
A.①② B.②③ C.①③ D.②④
3.如图所示的电路图,同时闭合两个开关能使小灯泡发亮的概率是 .
4.甲开车从A地前往B地送货,同时,乙从C地出发骑车前往B地,C在A,B两地之间且距离A地15千米.甲到达B地后以相同的速度立马返回A地,在A地休息半小时后,又以相同的速度前往B地送第二批货,乙出发后4小时遇上送货的甲,乙让甲捎上自己(上下车时间忽略不计),甲载上乙后以原速前进.甲、乙两人距离B地的路程y(千米)与时间x(小时)之间的函数关系如图所示.
(1)求甲第一次送货前往B地时,甲距离B地的路程y关于x的函数表达式.
(2)问在乙距离B地多远时,甲载上了乙?
(3)问乙比原计划早到多少时间?
5.【基础巩固】(1)如图1,△ABC和△ADE是直角三角形,∠ABC=∠ADE=90°,∠ACB=∠AED,求证:△DAB∽△EAC;
【尝试应用】(2)如图2,在Rt△ABC与RtAEDC中,直角顶点重合于点C,点D在AB上,∠BAC=∠DBC,且sin,连接AE,若BD=2,求AE的长;
【拓展提高】(3)如图3,若∠CAB=90°,∠E=∠ABC,tan,BD=5CD,过A作AQ⊥AD交EB延长线于Q,求的值.
浙江省中考数学考前冲刺每日一练30(精选全省各市历年经典真题,包含常考题型、易错题型、 小压轴、大压轴)参考答案与试题解析
一.选择题(共2小题)
1.沿正方体相邻的三条棱的中点截掉一部分,得到如图所示的几何体,则它的主视图是( )
A. B. C. D.
【分析】根据主视图的定义,画出这个几何体的主视图即可.
【解答】解:这个几何体的主视图如下:
故选:A.
【点评】本题考查简单组几何体的三视图,理解视图的定义,掌握简单几何体三视图的画法和形状是正确判断的前提.
2.如图,由两个正三角形组成的菱形内放入标记为①,②,③,④的四种不同大小的小正三角形5个,其中编号①的有2个.设未被覆盖的浅色阴影部分的周长为C1,深色阴影部分的周长为C2,若要求出C1﹣C2的值,只需知道其中两个小正三角形的边长,则这两个小三角形的编号为( )
A.①② B.②③ C.①③ D.②④
【分析】设标记为①,②,③,④的小正方形的边长分别是m、n、x、y,表示出C1和C2,即可解决问题.
【解答】解:设标记为①,②,③,④的小正方形的边长分别是m、n、x、y,
由题意得:C1=4x+m+2n=2(x+n)+2x+m,
C2=2y+4m=2(y+m)+2m,
∵x+n=y+m,
∴C1﹣C2=2x﹣m,
∴只需知道编号是①③的两个小正三角形的边长,即可求出C1﹣C2的值.
故选:C.
【点评】本题考查菱形的性质,等边三角形的性质,关键是由菱形、等边三角形的性质,用m、n、x、y表示出C1和C2.
二.填空题(共1小题)
3.如图所示的电路图,同时闭合两个开关能使小灯泡发亮的概率是 .
【分析】画树状图,共有6种等可能的结果,其中能使灯泡发光的结果有4种,再由概率公式求解即可.
【解答】解:把开关S1、S2、S3分别记为1、2、3,
画树状图如下:
共有6种等可能的结果,其中能使灯泡发光的结果有4种,
∴同时闭合两个开关能使小灯泡发亮的概率是=,
故答案为:.
【点评】此题考查的是用树状图法求概率.树状图法可以不重复不遗漏的列出所有可能的结果,适合两步或两步以上完成的事件.用到的知识点为:概率=所求情况数与总情况数之比.
三.解答题(共2小题)
4.甲开车从A地前往B地送货,同时,乙从C地出发骑车前往B地,C在A,B两地之间且距离A地15千米.甲到达B地后以相同的速度立马返回A地,在A地休息半小时后,又以相同的速度前往B地送第二批货,乙出发后4小时遇上送货的甲,乙让甲捎上自己(上下车时间忽略不计),甲载上乙后以原速前进.甲、乙两人距离B地的路程y(千米)与时间x(小时)之间的函数关系如图所示.
(1)求甲第一次送货前往B地时,甲距离B地的路程y关于x的函数表达式.
(2)问在乙距离B地多远时,甲载上了乙?
(3)问乙比原计划早到多少时间?
【分析】(1)根据题意题意得出甲第一次送货去B地的函数图象经过(0,75),(1.25,0),然后用待定系数法求出函数解析式;
(2)根据甲送货的速度不变,求出第二次送货的解析式,再把x=4代入解析式求y即可;
(3)求出甲第二次到B地的时间,和乙按原计划到B地的时间作差即可.
【解答】解:(1)由题意得,A、B两地间的路程为60+15=75千米,
甲第一次到达B地用时2.5÷2=1.25小时.
∴甲第一次送货去B地的函数图象经过(0,75),(1.25,0),
设甲第一次送货去B地的函数表达式为y=kx+b(k≠0),
把(0,75),(1.25,0)代入解析式得:
,
解得,
∴y关于x的函数表达式为y=﹣60x+75(0≤x≤1.25);
(2)甲第二次送货的函数图象经过(3,75),
∵甲送货的速度不变,
∴设甲第二次送货的函数表达式为y=﹣60x+m.
把(3,75)代入y=﹣60x+m,得75=﹣60×3+m,
解得m=255,
∴甲第二次送货的函数表达式为y=﹣60x+255,
当x=4时,y=15,
答:在乙距离B地15km时,甲载上了乙;
(3)把y=0代入y=﹣60x+255,
得0=﹣60x+255,
解得,
∵乙的图象经过点(0,60),
∴设乙的函数表达式为y=nx+60,
把(4,15)代入y=nx+60,
得15=4x+60,
解得.
∴乙比原计划早到时间为(小时).
答:乙比原计划早到小时.
【点评】本题考查一次函数和一元一次方程的应用,关键是找到等量关系列出函数解析式.
5.【基础巩固】(1)如图1,△ABC和△ADE是直角三角形,∠ABC=∠ADE=90°,∠ACB=∠AED,求证:△DAB∽△EAC;
【尝试应用】(2)如图2,在Rt△ABC与RtAEDC中,直角顶点重合于点C,点D在AB上,∠BAC=∠DBC,且sin,连接AE,若BD=2,求AE的长;
【拓展提高】(3)如图3,若∠CAB=90°,∠E=∠ABC,tan,BD=5CD,过A作AQ⊥AD交EB延长线于Q,求的值.
【分析】(1)通过证明△ABC∽△ADE,可得,∠BAC=∠DAE,可得结论;
(2)通过证明△CBD∽△CAE,可得,即可求解;
(3)由锐角三角函数可求∠E=30°,由直角三角形的性质可求BC=2AC=6a,AB=AC=3a,通过证明∠DAH∽△QAB,可求BQ的长,即可求解.
【解答】(1)证明:∵∠ABC=∠ADE=90°,∠ACB=∠AED,
∴△ABC∽△ADE,
∴,∠BAC=∠DAE,
∴∠CAE=∠BAD,
∴△DAB∽△EAC;
(2)解:∵∠BAC=∠DBC,sin,
∴sin∠BAC=sin∠DBC==,
∴AB=3BC,DE=3CD,
∴AC==2BC,CE==2CD,
∴=2,
∵∠ACB=∠DCE=90°,
∴∠BCD=∠ACE,
∴△CBD∽△CAE,
∴,
∵BD=2,
∴AE=4;
(3)解:如图3,在AC上截取CH=CD,连接DH,
∵tanE=,
∴∠E=30°,
∴∠E=∠ABC=30°,∠ABE=60°,
设AC=3a,则BC=2AC=6a,AB=AC=3a,
∵BD=5CD,
∴BD=5a,CD=a=CH,
∵∠ACB=90°﹣∠ABC=60°,
∴△CDH是等边三角形,
∴CH=CD=HD=a,∠CHD=120°,
∴AH=2a,
∵∠ABQ=180°﹣∠ABE=120°,
∴∠ABQ=∠AHD,
∵∠BAC=∠DAQ=90°,
∴∠DAH∽△QAB,
∴,
∴=,
∴BQ=a,
∴=.
【点评】本题是相似形综合题,考查了等边三角形的判定和性质,相似三角形的判定和性质,直角三角形的性质等知识,添加恰当辅助线构造相似三角形是解题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
