浙江省中考数学考前冲刺每日一练32(精选全省各市历年经典真题,包含常考题型、易错题型、 小压轴、大压轴)
文档属性
| 名称 | 浙江省中考数学考前冲刺每日一练32(精选全省各市历年经典真题,包含常考题型、易错题型、 小压轴、大压轴) |  | |
| 格式 | doc | ||
| 文件大小 | 365.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-24 09:27:45 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
浙江省中考数学考前冲刺每日一练32(精选全省各市历年经典真题,包含常考题型、易错题型、 小压轴、大压轴)
1.已知正多边形的一个外角是40°,则这个正多边形的边数是( )
A.九 B.八 C.七 D.六
2.如图,正六边形ABCDEF内接于⊙O,点M在上,则∠CME的度数为( )
A.36° B.45° C.60° D.75°
3.圆锥底面圆的直径和母线长均为4cm,则它的侧面积为 cm2.
4.小惠自编一题:“如图,在四边形ABCD中,对角线AC,BD交于点O,AC⊥BD,OB=OD.求证:四边形ABCD是菱形”,并将自己的证明过程与同学小洁交流.
小惠: 证明:∵AC⊥BD,OB=OD, ∴AC垂直平分BD. ∴AB=AD,CB=CD, ∴四边形ABCD是菱形. 小洁: 这个题目还缺少条件,需要补充一个条件才能证明.
若赞同小惠,请在第一个方框内打“√”;若赞成小洁,请你补充一个条件,并证明.
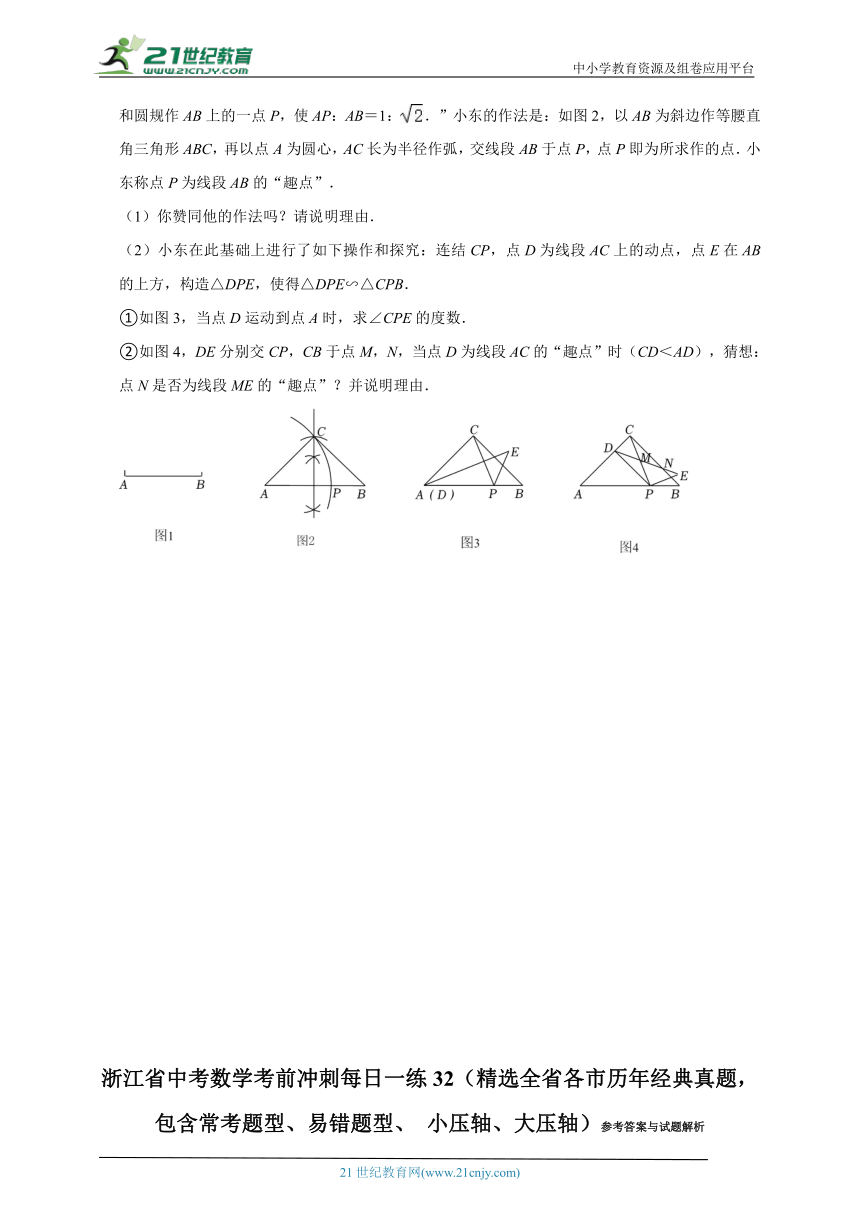
5.小东在做九上课本123页习题:“1:也是一个很有趣的比.已知线段AB(如图1),用直尺和圆规作AB上的一点P,使AP:AB=1:.”小东的作法是:如图2,以AB为斜边作等腰直角三角形ABC,再以点A为圆心,AC长为半径作弧,交线段AB于点P,点P即为所求作的点.小东称点P为线段AB的“趣点”.
(1)你赞同他的作法吗?请说明理由.
(2)小东在此基础上进行了如下操作和探究:连结CP,点D为线段AC上的动点,点E在AB的上方,构造△DPE,使得△DPE∽△CPB.
①如图3,当点D运动到点A时,求∠CPE的度数.
②如图4,DE分别交CP,CB于点M,N,当点D为线段AC的“趣点”时(CD<AD),猜想:点N是否为线段ME的“趣点”?并说明理由.
浙江省中考数学考前冲刺每日一练32(精选全省各市历年经典真题,包含常考题型、易错题型、 小压轴、大压轴)参考答案与试题解析
一.选择题(共1小题)
1.已知正多边形的一个外角是40°,则这个正多边形的边数是( )
A.九 B.八 C.七 D.六
【分析】应用多边形内角和定理进行计算即可得出答案.
【解答】解:根据题意可得,
这个正多边形的边数是=9.
故选:A.
【点评】本题主要考查了多边形的外角和,熟练掌握多边形的外角和定理进行求解是解决本题的关键.
二.填空题(共1小题)
2.圆锥底面圆的直径和母线长均为4cm,则它的侧面积为 8π cm2.
【分析】求出圆锥底面圆的周长,根据扇形的面积公式计算.
【解答】解:∵圆锥底面圆的直径为4cm,
∴圆锥底面圆的周长为4πcm,
则圆锥展开后所得扇形的弧长为4πcm,
∴它的侧面展开图的面积=×4π×4=8π(cm2),
故答案为:8π.
【点评】本题考查的是圆锥的计算,掌握圆锥的底面周长与展开后所得扇形的弧长相等是解题的关键.
三.解答题(共3小题)
3.小惠自编一题:“如图,在四边形ABCD中,对角线AC,BD交于点O,AC⊥BD,OB=OD.求证:四边形ABCD是菱形”,并将自己的证明过程与同学小洁交流.
小惠: 证明:∵AC⊥BD,OB=OD, ∴AC垂直平分BD. ∴AB=AD,CB=CD, ∴四边形ABCD是菱形. 小洁: 这个题目还缺少条件,需要补充一个条件才能证明.
若赞同小惠的证法,请在第一个方框内打“√”;若赞成小洁的说法,请你补充一个条件,并证明.
【分析】根据“对角线互相垂直的平行四边形是菱形”进行分析推理.
【解答】解:赞成小洁的说法,补充条件:OA=OC,证明如下:
∵OA=OC,OB=OD,
∴四边形ABCD是平行四边形,
又∵AC⊥BD,
∴平行四边形ABCD是菱形.
【点评】本题考查菱形的判定,掌握平行四边形的判定:(1)两组对边分别平行的四边形是平行四边形(2)两组对边分别相等的四边形是平行四边形(3)一组对边平行且相等的四边形是平行四边形(4)对角线互相平分的四边形是平行四边形以及菱形的判定方法:(1)四条边相等的四边形是菱形;(2)对角线互相垂直的平行四边形是菱形;(3)一组邻边相等的平行四边形是菱形,是解题关键.
4.小东在做九上课本123页习题:“1:也是一个很有趣的比.已知线段AB(如图1),用直尺和圆规作AB上的一点P,使AP:AB=1:.”小东的作法是:如图2,以AB为斜边作等腰直角三角形ABC,再以点A为圆心,AC长为半径作弧,交线段AB于点P,点P即为所求作的点.小东称点P为线段AB的“趣点”.
(1)你赞同他的作法吗?请说明理由.
(2)小东在此基础上进行了如下操作和探究:连结CP,点D为线段AC上的动点,点E在AB的上方,构造△DPE,使得△DPE∽△CPB.
①如图3,当点D运动到点A时,求∠CPE的度数.
②如图4,DE分别交CP,CB于点M,N,当点D为线段AC的“趣点”时(CD<AD),猜想:点N是否为线段ME的“趣点”?并说明理由.
【分析】(1)利用等腰三角形的性质证明,再利用AC=AP,即可得出结论;
(2)①由题意可得:∠CAB=∠B=45°,∠ACB=90°,AC=AP=BC,再求解∠ACP=∠APC=67.5°,∠CPB=112.5°,证明∠DPE=∠CPB=112.5°,从而可得答案;
②先证明△ADP∽△ACB,可得∠APD=45°,DP∥CB,再证明MP=MD=MC=MN,∠EMP=45°,∠MPE=90°,从而可得出结论.
【解答】解:(1)赞同,理由如下:
∵△ABC是等腰直角三角形,
∴AC=BC,∠A=∠B=45°,
∴cos45°=,
∵AC=AP,
∴,
∴点P为线段AB的“趣点”.
(2)①由题意得:∠CAB=∠B=45°,
∠ACB=90°,AC=AP=BC,
∴=67.5°,
∴∠BCP=90°﹣67.5°=22.5°,
∴∠CPB=180°﹣45°﹣22.5°=112.5°,
∵△DPE∽△CPB,D,A重合,
∴∠DPE=∠CPB=112.5°,
∴∠CPE=∠DPE+∠CPB﹣180°=45°;
②点N是线段ME的趣点,理由如下:
当点D为线段AC的趣点时(CD<AD),
∴,
∵AC=AP,
∴,
∵,∠A=∠A,
∴△ADP∽△ACB,
∴∠ADP=∠ACB=90°,
∴∠APD=45°,DP∥CB,
∴∠DPC=∠PCB=22.5°=∠PDE,
∴DM=PM,
∴∠MDC=∠MCD=90°﹣22.5°=67.5°,
∴MD=MC,
同理可得MC=MN,
∴MP=MD=MC=MN,
∵∠MDP=∠MPD=22.5°,∠E=∠B=45°,
∴∠EMP=45°,∠MPE=90°,
∴=,
∴点N是线段ME的“趣点”.
【点评】本题考查了等腰直角三角形的性质,锐角三角函数的应用,相似三角形的判定与性质,三角形的外角的性质,等腰三角形的判定与性质,理解新定义的含义,掌握特殊几何图形的性质是解题的关键.
5.(1)计算:;
(2)解不等式组:.
【分析】(1)先化简各式,然后再进行计算即可解答;
(2)按照解一元一次不等式组的步骤,进行计算即可解答.
【解答】解:(1)
=1﹣2+3
=4﹣2;
(2),
解不等式①得:x≤1;
解不等式②得:x≥﹣3,
∴原不等式组的解集为:﹣3≤x≤1.
【点评】本题考查了解一元一次不等式组,实数的运算,零指数幂,准确熟练地进行计算是解题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
浙江省中考数学考前冲刺每日一练32(精选全省各市历年经典真题,包含常考题型、易错题型、 小压轴、大压轴)
1.已知正多边形的一个外角是40°,则这个正多边形的边数是( )
A.九 B.八 C.七 D.六
2.如图,正六边形ABCDEF内接于⊙O,点M在上,则∠CME的度数为( )
A.36° B.45° C.60° D.75°
3.圆锥底面圆的直径和母线长均为4cm,则它的侧面积为 cm2.
4.小惠自编一题:“如图,在四边形ABCD中,对角线AC,BD交于点O,AC⊥BD,OB=OD.求证:四边形ABCD是菱形”,并将自己的证明过程与同学小洁交流.
小惠: 证明:∵AC⊥BD,OB=OD, ∴AC垂直平分BD. ∴AB=AD,CB=CD, ∴四边形ABCD是菱形. 小洁: 这个题目还缺少条件,需要补充一个条件才能证明.
若赞同小惠,请在第一个方框内打“√”;若赞成小洁,请你补充一个条件,并证明.
5.小东在做九上课本123页习题:“1:也是一个很有趣的比.已知线段AB(如图1),用直尺和圆规作AB上的一点P,使AP:AB=1:.”小东的作法是:如图2,以AB为斜边作等腰直角三角形ABC,再以点A为圆心,AC长为半径作弧,交线段AB于点P,点P即为所求作的点.小东称点P为线段AB的“趣点”.
(1)你赞同他的作法吗?请说明理由.
(2)小东在此基础上进行了如下操作和探究:连结CP,点D为线段AC上的动点,点E在AB的上方,构造△DPE,使得△DPE∽△CPB.
①如图3,当点D运动到点A时,求∠CPE的度数.
②如图4,DE分别交CP,CB于点M,N,当点D为线段AC的“趣点”时(CD<AD),猜想:点N是否为线段ME的“趣点”?并说明理由.
浙江省中考数学考前冲刺每日一练32(精选全省各市历年经典真题,包含常考题型、易错题型、 小压轴、大压轴)参考答案与试题解析
一.选择题(共1小题)
1.已知正多边形的一个外角是40°,则这个正多边形的边数是( )
A.九 B.八 C.七 D.六
【分析】应用多边形内角和定理进行计算即可得出答案.
【解答】解:根据题意可得,
这个正多边形的边数是=9.
故选:A.
【点评】本题主要考查了多边形的外角和,熟练掌握多边形的外角和定理进行求解是解决本题的关键.
二.填空题(共1小题)
2.圆锥底面圆的直径和母线长均为4cm,则它的侧面积为 8π cm2.
【分析】求出圆锥底面圆的周长,根据扇形的面积公式计算.
【解答】解:∵圆锥底面圆的直径为4cm,
∴圆锥底面圆的周长为4πcm,
则圆锥展开后所得扇形的弧长为4πcm,
∴它的侧面展开图的面积=×4π×4=8π(cm2),
故答案为:8π.
【点评】本题考查的是圆锥的计算,掌握圆锥的底面周长与展开后所得扇形的弧长相等是解题的关键.
三.解答题(共3小题)
3.小惠自编一题:“如图,在四边形ABCD中,对角线AC,BD交于点O,AC⊥BD,OB=OD.求证:四边形ABCD是菱形”,并将自己的证明过程与同学小洁交流.
小惠: 证明:∵AC⊥BD,OB=OD, ∴AC垂直平分BD. ∴AB=AD,CB=CD, ∴四边形ABCD是菱形. 小洁: 这个题目还缺少条件,需要补充一个条件才能证明.
若赞同小惠的证法,请在第一个方框内打“√”;若赞成小洁的说法,请你补充一个条件,并证明.
【分析】根据“对角线互相垂直的平行四边形是菱形”进行分析推理.
【解答】解:赞成小洁的说法,补充条件:OA=OC,证明如下:
∵OA=OC,OB=OD,
∴四边形ABCD是平行四边形,
又∵AC⊥BD,
∴平行四边形ABCD是菱形.
【点评】本题考查菱形的判定,掌握平行四边形的判定:(1)两组对边分别平行的四边形是平行四边形(2)两组对边分别相等的四边形是平行四边形(3)一组对边平行且相等的四边形是平行四边形(4)对角线互相平分的四边形是平行四边形以及菱形的判定方法:(1)四条边相等的四边形是菱形;(2)对角线互相垂直的平行四边形是菱形;(3)一组邻边相等的平行四边形是菱形,是解题关键.
4.小东在做九上课本123页习题:“1:也是一个很有趣的比.已知线段AB(如图1),用直尺和圆规作AB上的一点P,使AP:AB=1:.”小东的作法是:如图2,以AB为斜边作等腰直角三角形ABC,再以点A为圆心,AC长为半径作弧,交线段AB于点P,点P即为所求作的点.小东称点P为线段AB的“趣点”.
(1)你赞同他的作法吗?请说明理由.
(2)小东在此基础上进行了如下操作和探究:连结CP,点D为线段AC上的动点,点E在AB的上方,构造△DPE,使得△DPE∽△CPB.
①如图3,当点D运动到点A时,求∠CPE的度数.
②如图4,DE分别交CP,CB于点M,N,当点D为线段AC的“趣点”时(CD<AD),猜想:点N是否为线段ME的“趣点”?并说明理由.
【分析】(1)利用等腰三角形的性质证明,再利用AC=AP,即可得出结论;
(2)①由题意可得:∠CAB=∠B=45°,∠ACB=90°,AC=AP=BC,再求解∠ACP=∠APC=67.5°,∠CPB=112.5°,证明∠DPE=∠CPB=112.5°,从而可得答案;
②先证明△ADP∽△ACB,可得∠APD=45°,DP∥CB,再证明MP=MD=MC=MN,∠EMP=45°,∠MPE=90°,从而可得出结论.
【解答】解:(1)赞同,理由如下:
∵△ABC是等腰直角三角形,
∴AC=BC,∠A=∠B=45°,
∴cos45°=,
∵AC=AP,
∴,
∴点P为线段AB的“趣点”.
(2)①由题意得:∠CAB=∠B=45°,
∠ACB=90°,AC=AP=BC,
∴=67.5°,
∴∠BCP=90°﹣67.5°=22.5°,
∴∠CPB=180°﹣45°﹣22.5°=112.5°,
∵△DPE∽△CPB,D,A重合,
∴∠DPE=∠CPB=112.5°,
∴∠CPE=∠DPE+∠CPB﹣180°=45°;
②点N是线段ME的趣点,理由如下:
当点D为线段AC的趣点时(CD<AD),
∴,
∵AC=AP,
∴,
∵,∠A=∠A,
∴△ADP∽△ACB,
∴∠ADP=∠ACB=90°,
∴∠APD=45°,DP∥CB,
∴∠DPC=∠PCB=22.5°=∠PDE,
∴DM=PM,
∴∠MDC=∠MCD=90°﹣22.5°=67.5°,
∴MD=MC,
同理可得MC=MN,
∴MP=MD=MC=MN,
∵∠MDP=∠MPD=22.5°,∠E=∠B=45°,
∴∠EMP=45°,∠MPE=90°,
∴=,
∴点N是线段ME的“趣点”.
【点评】本题考查了等腰直角三角形的性质,锐角三角函数的应用,相似三角形的判定与性质,三角形的外角的性质,等腰三角形的判定与性质,理解新定义的含义,掌握特殊几何图形的性质是解题的关键.
5.(1)计算:;
(2)解不等式组:.
【分析】(1)先化简各式,然后再进行计算即可解答;
(2)按照解一元一次不等式组的步骤,进行计算即可解答.
【解答】解:(1)
=1﹣2+3
=4﹣2;
(2),
解不等式①得:x≤1;
解不等式②得:x≥﹣3,
∴原不等式组的解集为:﹣3≤x≤1.
【点评】本题考查了解一元一次不等式组,实数的运算,零指数幂,准确熟练地进行计算是解题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
