浙江省中考数学考前冲刺每日一练33(精选全省各市历年经典真题,包含常考题型、易错题型、 小压轴、大压轴)
文档属性
| 名称 | 浙江省中考数学考前冲刺每日一练33(精选全省各市历年经典真题,包含常考题型、易错题型、 小压轴、大压轴) |  | |
| 格式 | doc | ||
| 文件大小 | 358.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-24 09:27:45 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
浙江省中考数学考前冲刺每日一练33(精选全省各市历年经典真题,包含常考题型、易错题型、 小压轴、大压轴)
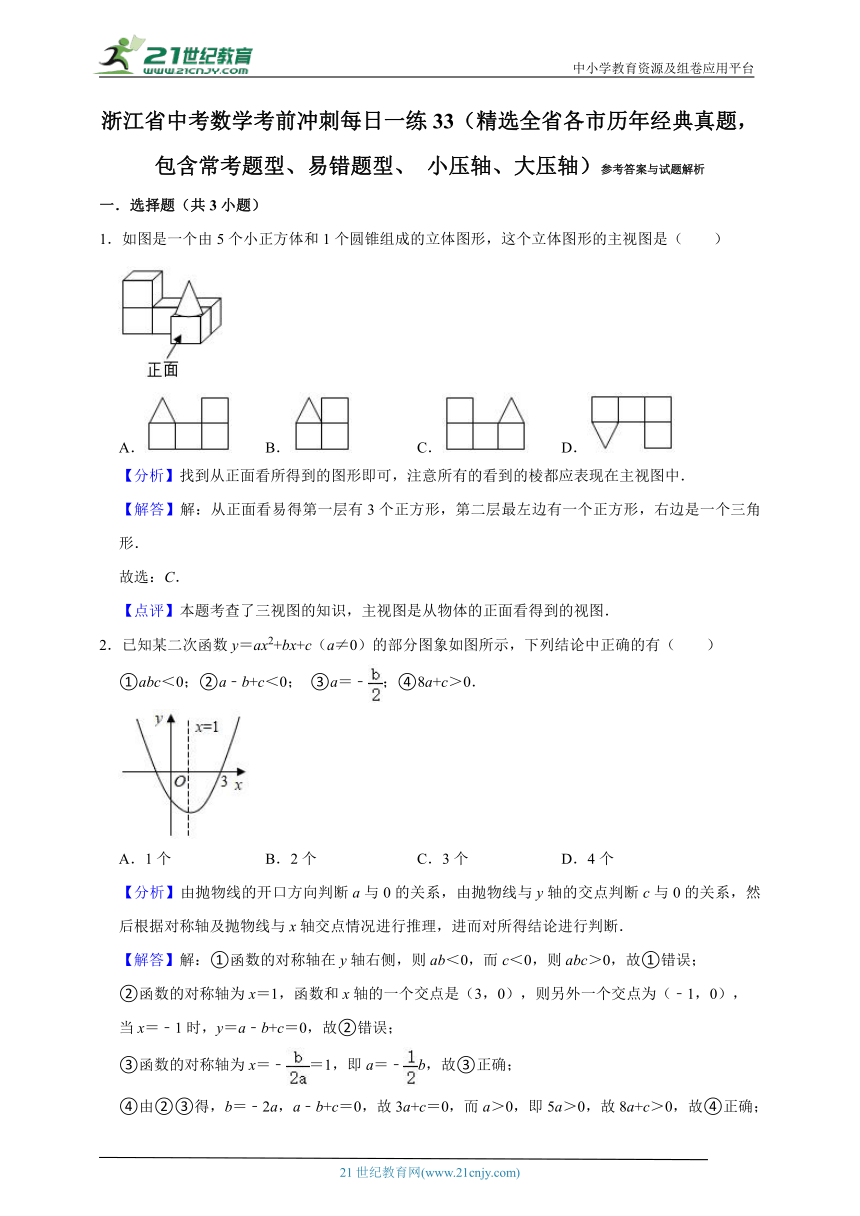
1.如图是一个由5个小正方体和1个圆锥组成的立体图形,这个立体图形的主视图是( )
A. B. C. D.
2.已知某二次函数y=ax2+bx+c(a≠0)的部分图象如图所示,下列结论中正确的有( )
①abc<0;②a﹣b+c<0; ③a=﹣;④8a+c>0.
A.1个 B.2个 C.3个 D.4个
3.两直角边之比为:1的一个直角三角形按图1的方式分测成两个直角三角形,将分割后的两个直角三角形按图2中的①、②两种方式放置,设①中的阴影部分面积为S1,②中的阴影部分面积为S2.则S1:S2的值为( )
A. B. C. D.
4.数据6,5,x,4,7的平均数是5,那么这组数据的方差为 .
5.如图,平行四边形ABCD的顶点A在双曲线y=﹣(x<0)上,点B坐标为(﹣2,0),且OA=AB,顶点C,D在双曲线y=(k<0,x>0)上,AD与x轴交于点E.四边形BCDE面积是△ABE的面积的2倍,则k= .
浙江省中考数学考前冲刺每日一练33(精选全省各市历年经典真题,包含常考题型、易错题型、 小压轴、大压轴)参考答案与试题解析
一.选择题(共3小题)
1.如图是一个由5个小正方体和1个圆锥组成的立体图形,这个立体图形的主视图是( )
A. B. C. D.
【分析】找到从正面看所得到的图形即可,注意所有的看到的棱都应表现在主视图中.
【解答】解:从正面看易得第一层有3个正方形,第二层最左边有一个正方形,右边是一个三角形.
故选:C.
【点评】本题考查了三视图的知识,主视图是从物体的正面看得到的视图.
2.已知某二次函数y=ax2+bx+c(a≠0)的部分图象如图所示,下列结论中正确的有( )
①abc<0;②a﹣b+c<0; ③a=﹣;④8a+c>0.
A.1个 B.2个 C.3个 D.4个
【分析】由抛物线的开口方向判断a与0的关系,由抛物线与y轴的交点判断c与0的关系,然后根据对称轴及抛物线与x轴交点情况进行推理,进而对所得结论进行判断.
【解答】解:①函数的对称轴在y轴右侧,则ab<0,而c<0,则abc>0,故①错误;
②函数的对称轴为x=1,函数和x轴的一个交点是(3,0),则另外一个交点为(﹣1,0),
当x=﹣1时,y=a﹣b+c=0,故②错误;
③函数的对称轴为x=﹣=1,即a=﹣b,故③正确;
④由②③得,b=﹣2a,a﹣b+c=0,故3a+c=0,而a>0,即5a>0,故8a+c>0,故④正确;
故选:B.
【点评】主要考查图象与二次函数系数之间的关系,会利用对称轴的范围求2a与b的关系,以及二次函数与方程之间的转换等.
3.两直角边之比为:1的一个直角三角形按图1的方式分测成两个直角三角形,将分割后的两个直角三角形按图2中的①、②两种方式放置,设①中的阴影部分面积为S1,②中的阴影部分面积为S2.则S1:S2的值为( )
A. B. C. D.
【分析】通过证得△ACD∽△CBD,得出,由图2①可知OB=OD'=OC′,即可证得S1=S△BC'D=S△BCD,图2②中,利用△ACD∽△CBD,证得S2=S△ADC﹣S△BCD=S△BCD,即可证得S1:S2=.
【解答】解:如图1,∵∠ACD+∠BCD=90°=∠BCD+∠B,
∴∠ACD=∠B,
∵∠ADC=∠CDB=90°,
∴△ACD∽△CBD,
∴,
由图2①,∵∠ACD=∠C′BD′,∠BD′C'=90°,
∴OB=OD′,∠C'=∠AD′C',
∴OB=OD'=OC′,
∴S1=S△BC'D=S△BCD
由图2②,∵△ACD∽△CBD,
∴△ACD∽△C′BD,
∴,
∴2S△BC′D=S△ACD,
∴S2=S△ADC﹣S△BCD=S△BCD,
∴S1:S2=,
故选:A.
【点评】本题考查了三角形的面积,相似三角形的判定和性质,灵活运用这些性质解决问题是本题的关键.
二.填空题(共2小题)
4.数据6,5,x,4,7的平均数是5,那么这组数据的方差为 2 .
【分析】先根据平均数的定义得到6+5+x+4+7=25,解得x=3,然后根据方差公式计算.
【解答】解:根据题意得6+5+x+4+7=25,
解得x=3,
这组数据的方差为[(6﹣5)2+(5﹣5)2+(3﹣5)2+(4﹣5)2+(7﹣5)2]=2.
故答案为2.
【点评】本题考查方差的定义:一般地设n个数据,x1,x2,…xn的平均数为,则方差S2=[(x1﹣)2+(x2﹣)2+…+(xn﹣)2],它反映了一组数据的波动大小,方差越大,波动性越大,反之也成立.也考查了平均数.
5.如图,平行四边形ABCD的顶点A在双曲线y=﹣(x<0)上,点B坐标为(﹣2,0),且OA=AB,顶点C,D在双曲线y=(k<0,x>0)上,AD与x轴交于点E.四边形BCDE面积是△ABE的面积的2倍,则k= ﹣ .
【分析】根据题意,可以推出AF=2和=2,继而求得点D的纵坐标,再利用△BAF≌△CDG(AAS)推出CG=BF=1,DG=AF=2,继而得到点C坐标,代入解析式可得k值.
【解答】解:作AF⊥BO,
∵OA=AB,OB=2,
∴BF=OF=1,
∴AF=2,
设S△ABE=x,S△DBE=y,
∵S四边形BCDE=2S△ABE,
∴x+y+y=2x,
∴2y=x,
∴,
∴D(﹣k,﹣1),
过点C、D分别作x轴,y轴平行线,交于点G,
∵AB∥CD,AF∥DG,
∴∠BAF=∠CDG,
在△BAF和△CDG中,
,
∴△BAF≌△CDG(AAS),
∴CG=BF=1,DG=AF=2,
∴C(﹣k﹣1,﹣3),
将点C的坐标代入y=得,
﹣3(﹣k﹣1)=k,
解得k=﹣.
故答案为:﹣.
【点评】本题考查了反比例函数图象上点的坐标特征和平行四边形的性质,熟练掌握平行四边形性质是解答本题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
浙江省中考数学考前冲刺每日一练33(精选全省各市历年经典真题,包含常考题型、易错题型、 小压轴、大压轴)
1.如图是一个由5个小正方体和1个圆锥组成的立体图形,这个立体图形的主视图是( )
A. B. C. D.
2.已知某二次函数y=ax2+bx+c(a≠0)的部分图象如图所示,下列结论中正确的有( )
①abc<0;②a﹣b+c<0; ③a=﹣;④8a+c>0.
A.1个 B.2个 C.3个 D.4个
3.两直角边之比为:1的一个直角三角形按图1的方式分测成两个直角三角形,将分割后的两个直角三角形按图2中的①、②两种方式放置,设①中的阴影部分面积为S1,②中的阴影部分面积为S2.则S1:S2的值为( )
A. B. C. D.
4.数据6,5,x,4,7的平均数是5,那么这组数据的方差为 .
5.如图,平行四边形ABCD的顶点A在双曲线y=﹣(x<0)上,点B坐标为(﹣2,0),且OA=AB,顶点C,D在双曲线y=(k<0,x>0)上,AD与x轴交于点E.四边形BCDE面积是△ABE的面积的2倍,则k= .
浙江省中考数学考前冲刺每日一练33(精选全省各市历年经典真题,包含常考题型、易错题型、 小压轴、大压轴)参考答案与试题解析
一.选择题(共3小题)
1.如图是一个由5个小正方体和1个圆锥组成的立体图形,这个立体图形的主视图是( )
A. B. C. D.
【分析】找到从正面看所得到的图形即可,注意所有的看到的棱都应表现在主视图中.
【解答】解:从正面看易得第一层有3个正方形,第二层最左边有一个正方形,右边是一个三角形.
故选:C.
【点评】本题考查了三视图的知识,主视图是从物体的正面看得到的视图.
2.已知某二次函数y=ax2+bx+c(a≠0)的部分图象如图所示,下列结论中正确的有( )
①abc<0;②a﹣b+c<0; ③a=﹣;④8a+c>0.
A.1个 B.2个 C.3个 D.4个
【分析】由抛物线的开口方向判断a与0的关系,由抛物线与y轴的交点判断c与0的关系,然后根据对称轴及抛物线与x轴交点情况进行推理,进而对所得结论进行判断.
【解答】解:①函数的对称轴在y轴右侧,则ab<0,而c<0,则abc>0,故①错误;
②函数的对称轴为x=1,函数和x轴的一个交点是(3,0),则另外一个交点为(﹣1,0),
当x=﹣1时,y=a﹣b+c=0,故②错误;
③函数的对称轴为x=﹣=1,即a=﹣b,故③正确;
④由②③得,b=﹣2a,a﹣b+c=0,故3a+c=0,而a>0,即5a>0,故8a+c>0,故④正确;
故选:B.
【点评】主要考查图象与二次函数系数之间的关系,会利用对称轴的范围求2a与b的关系,以及二次函数与方程之间的转换等.
3.两直角边之比为:1的一个直角三角形按图1的方式分测成两个直角三角形,将分割后的两个直角三角形按图2中的①、②两种方式放置,设①中的阴影部分面积为S1,②中的阴影部分面积为S2.则S1:S2的值为( )
A. B. C. D.
【分析】通过证得△ACD∽△CBD,得出,由图2①可知OB=OD'=OC′,即可证得S1=S△BC'D=S△BCD,图2②中,利用△ACD∽△CBD,证得S2=S△ADC﹣S△BCD=S△BCD,即可证得S1:S2=.
【解答】解:如图1,∵∠ACD+∠BCD=90°=∠BCD+∠B,
∴∠ACD=∠B,
∵∠ADC=∠CDB=90°,
∴△ACD∽△CBD,
∴,
由图2①,∵∠ACD=∠C′BD′,∠BD′C'=90°,
∴OB=OD′,∠C'=∠AD′C',
∴OB=OD'=OC′,
∴S1=S△BC'D=S△BCD
由图2②,∵△ACD∽△CBD,
∴△ACD∽△C′BD,
∴,
∴2S△BC′D=S△ACD,
∴S2=S△ADC﹣S△BCD=S△BCD,
∴S1:S2=,
故选:A.
【点评】本题考查了三角形的面积,相似三角形的判定和性质,灵活运用这些性质解决问题是本题的关键.
二.填空题(共2小题)
4.数据6,5,x,4,7的平均数是5,那么这组数据的方差为 2 .
【分析】先根据平均数的定义得到6+5+x+4+7=25,解得x=3,然后根据方差公式计算.
【解答】解:根据题意得6+5+x+4+7=25,
解得x=3,
这组数据的方差为[(6﹣5)2+(5﹣5)2+(3﹣5)2+(4﹣5)2+(7﹣5)2]=2.
故答案为2.
【点评】本题考查方差的定义:一般地设n个数据,x1,x2,…xn的平均数为,则方差S2=[(x1﹣)2+(x2﹣)2+…+(xn﹣)2],它反映了一组数据的波动大小,方差越大,波动性越大,反之也成立.也考查了平均数.
5.如图,平行四边形ABCD的顶点A在双曲线y=﹣(x<0)上,点B坐标为(﹣2,0),且OA=AB,顶点C,D在双曲线y=(k<0,x>0)上,AD与x轴交于点E.四边形BCDE面积是△ABE的面积的2倍,则k= ﹣ .
【分析】根据题意,可以推出AF=2和=2,继而求得点D的纵坐标,再利用△BAF≌△CDG(AAS)推出CG=BF=1,DG=AF=2,继而得到点C坐标,代入解析式可得k值.
【解答】解:作AF⊥BO,
∵OA=AB,OB=2,
∴BF=OF=1,
∴AF=2,
设S△ABE=x,S△DBE=y,
∵S四边形BCDE=2S△ABE,
∴x+y+y=2x,
∴2y=x,
∴,
∴D(﹣k,﹣1),
过点C、D分别作x轴,y轴平行线,交于点G,
∵AB∥CD,AF∥DG,
∴∠BAF=∠CDG,
在△BAF和△CDG中,
,
∴△BAF≌△CDG(AAS),
∴CG=BF=1,DG=AF=2,
∴C(﹣k﹣1,﹣3),
将点C的坐标代入y=得,
﹣3(﹣k﹣1)=k,
解得k=﹣.
故答案为:﹣.
【点评】本题考查了反比例函数图象上点的坐标特征和平行四边形的性质,熟练掌握平行四边形性质是解答本题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
