浙江省中考数学考前冲刺每日一练35(精选全省各市历年经典真题,包含常考题型、易错题型、 小压轴、大压轴)
文档属性
| 名称 | 浙江省中考数学考前冲刺每日一练35(精选全省各市历年经典真题,包含常考题型、易错题型、 小压轴、大压轴) |

|
|
| 格式 | doc | ||
| 文件大小 | 461.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-24 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
浙江省中考数学考前冲刺每日一练35(精选全省各市历年经典真题,包含常考题型、易错题型、 小压轴、大压轴)
1.由新型肺炎疫情影响,各类消毒液需求量大增,卫健委积极推动部分消毒液紧急上市,有效缓解消毒液供需矛盾.根据商场调查,某种消毒液的大瓶装(5kg)和小瓶装(2.5kg)两种产品的销售数量(按瓶计算)比为3:4.某厂每天生产这种消毒液25t,这些消毒液应该分装大、小瓶两种产品各多少瓶?设这些消毒液应该分装x大瓶、y小瓶.根据题意可列方程组( )
A. B. C. D.
2.如图,在平面直角坐标系中,一次函数y=﹣x+2的图象与y轴正半轴、x轴的正半轴分别交于A,B两点,点M是线段AB上的动点,⊙M的半径为1,当⊙M与坐标轴相切时,则MA的长度是 .
3.已知抛物线y=x2﹣2x+c(c是常数)经过点A(﹣1,0).
(1)求该抛物线解析式;
(2)当0<x<3时,求y的取值范围;
(3)若P(a,b)为抛物线上的个动点,P关于原点的对称点为P',当点P′落在该抛物线上时,求a的值.
4.为了解某校九年级学生的理化实验操作情况,随机抽查了40名同学实验操作的得分.根据获取的样本数据,制作了如下的条形统计图和扇形统计图.请根据相关信息,解答下列问题:
(Ⅰ)扇形 ①的圆心角的大小是 ;
(Ⅱ)求这40个样本数据的平均数、众数、中位数;
(Ⅲ)若该校九年级共有320名学生,估计该校理化实验操作得满分(10分)有多少人.
5.【基础巩固】
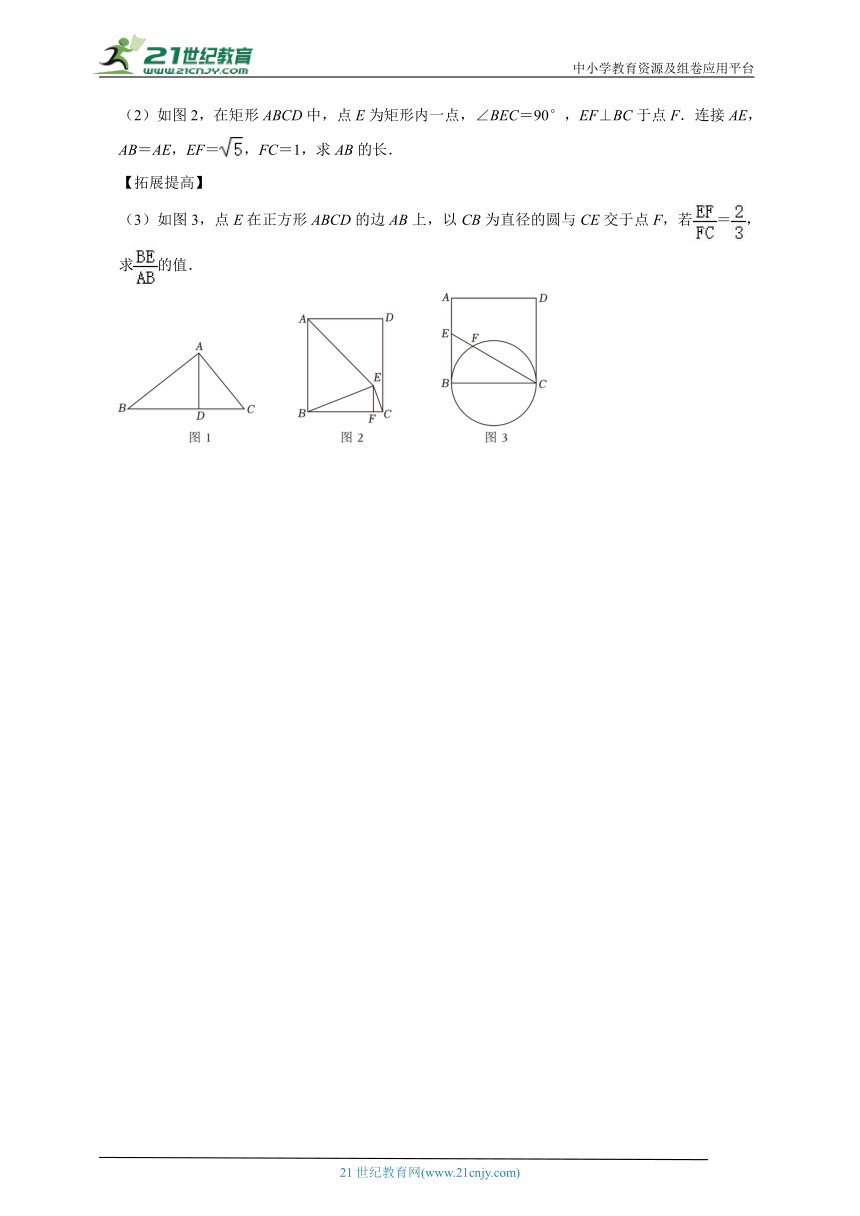
(1)如图1,在Rt△ABC中,∠BAC=90°,AD⊥BC于点D,求证:AD2=BD CD.
【尝试应用】
(2)如图2,在矩形ABCD中,点E为矩形内一点,∠BEC=90°,EF⊥BC于点F.连接AE,AB=AE,EF=,FC=1,求AB的长.
【拓展提高】
(3)如图3,点E在正方形ABCD的边AB上,以CB为直径的圆与CE交于点F,若=,求的值.
浙江省中考数学考前冲刺每日一练35(精选全省各市历年经典真题,包含常考题型、易错题型、 小压轴、大压轴)参考答案与试题解析
一.选择题(共1小题)
1.由新型肺炎疫情影响,各类消毒液需求量大增,卫健委积极推动部分消毒液紧急上市,有效缓解消毒液供需矛盾.根据商场调查,某种消毒液的大瓶装(5kg)和小瓶装(2.5kg)两种产品的销售数量(按瓶计算)比为3:4.某厂每天生产这种消毒液25t,这些消毒液应该分装大、小瓶两种产品各多少瓶?设这些消毒液应该分装x大瓶、y小瓶.根据题意可列方程组( )
A.
B.
C.
D.
【分析】设应该分装大小瓶两种产品x瓶、y瓶,根据大瓶装(500g)和小瓶装(250g)两种产品的销售数量比为3:4,每天生产这种消毒液3:4列方程组成方程组即可.
【解答】解:设这些消毒液应该分装x大瓶、y小瓶.由题意得,.
故选:D.
【点评】此题考查列二元一次方程组解决实际问题,注意题目蕴含的数量关系,正确列式解答即可.
二.填空题(共1小题)
2.如图,在平面直角坐标系中,一次函数y=﹣x+2的图象与y轴正半轴、x轴的正半轴分别交于A,B两点,点M是线段AB上的动点,⊙M的半径为1,当⊙M与坐标轴相切时,则MA的长度是 或 .
【分析】求出A、B的坐标,得到OA,OB的长,由勾股定理求出AB的长,当⊙M与y轴相切时,由△AHM∽△AOB,得到HM:OB=AM:AB,即可求出AM=;当⊙M与x轴相切时,由△BMK∽△BAO,得到KM:AO=BM:AB,求出BM的长,即可得到AM的长,于是得到MA的长度.
【解答】解:当x=0时,y=2,
∴A的坐标是(0,2),
∴OA=2,
当y=0时,0=﹣x+2,得到x=4,
∴B的坐标是(4,0),
∴OB=4,
∴AB==2,
当⊙M与y轴相切时,切点是H,
连接MH,
∴MH⊥AO,
∵BO⊥AO,
∴MH∥BO,
∴△AHM∽△AOB,
∴HM:OB=AM:AB,
∵⊙M的半径为1,
∴MH=1,
∴1:4=AM:2,
∴AM=;
当⊙M与x轴相切时,切点是K,
连接MK,
∴MK⊥OB,
∵AO⊥OB,
∴MK∥AO,
∴△BMK∽△BAO,
∴KM:AO=BM:AB,
∴1:2=BM:2,
∴MB=,
∴AM=AB﹣BM=2﹣=,
∴MA的长度是或.
故答案为:或.
【点评】本题考查切线的性质,相似三角形的判定和性质,一次函数的性质,一次函数图象上坐标的特征,关键是要分两种情况讨论.
三.解答题(共3小题)
3.已知抛物线y=x2﹣2x+c(c是常数)经过点A(﹣1,0).
(1)求该抛物线解析式;
(2)当0<x<3时,求y的取值范围;
(3)若P(a,b)为抛物线上的个动点,P关于原点的对称点为P',当点P′落在该抛物线上时,求a的值.
【分析】(1)根据抛物线y=x2﹣2x+c(c是常数)经过点A(﹣1,0),可以求得c的值,从而可以得到抛物线的解析式;
(2)根据二次函数的性质,可以得到当0<x<3时,y的取值范围;
(3)根据P(m,t)为抛物线上的一个动点,P关于原点的对称点为P′,点P′落在该抛物线上.可以求得a的值.
【解答】解:(1)∵抛物线y=x2﹣2x+c(c是常数)经过点A(﹣1,0),
∴0=1+2+c,
解得c=﹣3,
∴抛物线解析式为y=x2﹣2x﹣3;
(2)∵y=x2﹣2x﹣3=(x﹣1)2﹣4,
∴该抛物线的开口方向向上,对称轴是直线x=1,顶点坐标为(1,﹣4),
∴x=1时,函数有最小值﹣4,
∵当x=0时,y=﹣3,当x=3时,y=x2﹣2x﹣3=0,
∴当0<x<3时,y的取值范围是﹣4≤y<0;
(3)∵P(a,b)为抛物线上的个动点,P关于原点的对称点为P',
∴点P′的坐标为(﹣a,﹣b),
又∵P′落在该抛物线上,
∴,
解得或,
即a的值是或﹣.
【点评】本题考查了二次函数图象上点的坐标特征、待定系数法求二次函数的解析式,二次函数的性质、关于原点对称的点的坐标,解答本题的关键是明确题意,利用二次函数的性质解答.
4.为了解某校九年级学生的理化实验操作情况,随机抽查了40名同学实验操作的得分.根据获取的样本数据,制作了如下的条形统计图和扇形统计图.请根据相关信息,解答下列问题:
(Ⅰ)扇形 ①的圆心角的大小是 36° ;
(Ⅱ)求这40个样本数据的平均数、众数、中位数;
(Ⅲ)若该校九年级共有320名学生,估计该校理化实验操作得满分(10分)有多少人.
【分析】(Ⅰ)用360°乘以①所占的百分比,计算即可得解;
(Ⅱ)根据平均数的定义;众数是一组数据中出现次数最多的数据,注意众数可以不止一个;找中位数要把数据按从小到大的顺序排列,位于最中间的一个数(或两个数的平均数)为中位数分别解答;
(Ⅲ)用九年级总人数乘以满分的人数所占的份数计算即可得解.
【解答】解:(Ⅰ)360°×(1﹣15%﹣27.5%﹣30%﹣17.5%)
=360°×10%
=36°;
故答案为:36°.
(Ⅱ)∵==8.3,
∴平均数是8.3;
∵9出现了12次,次数最多,
∴众数是9;
∵将40个数字按从小到大排列,中间的两个数都是8,
∴中位数是=8;
(Ⅲ)∵320×=56(人),
∴满分约有56人.
【点评】本题属于基础题,考查了确定一组数据的中位数和众数的能力.一些学生往往对这个概念掌握不清楚,计算方法不明确而误选其它选项,注意找中位数的时候一定要先排好顺序,然后再根据奇数和偶数个来确定中位数,如果数据有奇数个,则正中间的数字即为所求,如果是偶数个则找中间两位数的平均数.
5.【基础巩固】
(1)如图1,在Rt△ABC中,∠BAC=90°,AD⊥BC于点D,求证:AD2=BD CD.
【尝试应用】
(2)如图2,在矩形ABCD中,点E为矩形内一点,∠BEC=90°,EF⊥BC于点F.连接AE,AB=AE,EF=,FC=1,求AB的长.
【拓展提高】
(3)如图3,点E在正方形ABCD的边AB上,以CB为直径的圆与CE交于点F,若=,求的值.
【分析】(1)利用等角的余角相等得到∠B=∠DAC,则可判断Rt△ADB∽Rt△CDA,所以AD:CD=BD:AD,然后根据比例的性质即可得到结论;
(2)证明Rt△EFB∽Rt△CFE,可得EF2=BF CF,可求得BF=5,根据勾股定理求出BE=,过A作AH⊥BE于H,根据等腰三角形的性质得BH=BE=,再证Rt△ABH∽Rt△BEF,根据相似三角形的性质即可求解;
(3)连接BF,由CB为直径可得∠BFC=90°,证明Rt△CFB∽Rt△BFE,根据相似三角形的性质得=,可得BF2=EF CF,设EF=2k,则FC=3k,可得BF=k,根据正方形的性质得AB=CB,即可求解.
【解答】(1)证明:∵AD⊥BC于点D,
∴∠ADB=∠ADC=90°,
∴∠B+∠BAD=90°,
又∵∠BAD+∠DAC=∠BAC=90°,
∴∠B=∠DAC,
∴Rt△ADB∽Rt△CDA,
∴AD:CD=BD:AD,
∴AD2=CD BD;
(2)解:同(1)可得Rt△EFB∽Rt△CFE,
∴EF2=BF CF,
∵EF=,FC=1,
∴BF=5,
∴BE==,
过A作AH⊥BE于H,
∴∠AHB=∠BFE=90°,
∵AB=AE,
∴BH=BE=,
∵四边形ABCD是矩形,
∴∠ABC=90°,
∴∠ABH+∠EBF=∠BEF+∠EBF=90°,
∴∠ABH=∠BEF,
∴Rt△ABH∽Rt△BEF,
∴,即,
∴AB=3;
(3)解:连接BF,
∵CB为直径,
∴∠BFC=90°,
∵四边形ABCD是正方形,
∴∠ABC=90°,
同(1)可得Rt△CFB∽Rt△BFE,
∴=,
∴BF2=EF CF,
∵,
设EF=2k,则FC=3k,
∴BF=k,
∴===,
∵四边形ABCD是正方形,
∴AB=CB,
∴=.
【点评】本题是圆的综合题,考查了正方形性质,等腰三角形性质,相似三角形判定和性质,圆的有关性质等知识,解决问题的关键是作辅助线,构造相似三角形.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
浙江省中考数学考前冲刺每日一练35(精选全省各市历年经典真题,包含常考题型、易错题型、 小压轴、大压轴)
1.由新型肺炎疫情影响,各类消毒液需求量大增,卫健委积极推动部分消毒液紧急上市,有效缓解消毒液供需矛盾.根据商场调查,某种消毒液的大瓶装(5kg)和小瓶装(2.5kg)两种产品的销售数量(按瓶计算)比为3:4.某厂每天生产这种消毒液25t,这些消毒液应该分装大、小瓶两种产品各多少瓶?设这些消毒液应该分装x大瓶、y小瓶.根据题意可列方程组( )
A. B. C. D.
2.如图,在平面直角坐标系中,一次函数y=﹣x+2的图象与y轴正半轴、x轴的正半轴分别交于A,B两点,点M是线段AB上的动点,⊙M的半径为1,当⊙M与坐标轴相切时,则MA的长度是 .
3.已知抛物线y=x2﹣2x+c(c是常数)经过点A(﹣1,0).
(1)求该抛物线解析式;
(2)当0<x<3时,求y的取值范围;
(3)若P(a,b)为抛物线上的个动点,P关于原点的对称点为P',当点P′落在该抛物线上时,求a的值.
4.为了解某校九年级学生的理化实验操作情况,随机抽查了40名同学实验操作的得分.根据获取的样本数据,制作了如下的条形统计图和扇形统计图.请根据相关信息,解答下列问题:
(Ⅰ)扇形 ①的圆心角的大小是 ;
(Ⅱ)求这40个样本数据的平均数、众数、中位数;
(Ⅲ)若该校九年级共有320名学生,估计该校理化实验操作得满分(10分)有多少人.
5.【基础巩固】
(1)如图1,在Rt△ABC中,∠BAC=90°,AD⊥BC于点D,求证:AD2=BD CD.
【尝试应用】
(2)如图2,在矩形ABCD中,点E为矩形内一点,∠BEC=90°,EF⊥BC于点F.连接AE,AB=AE,EF=,FC=1,求AB的长.
【拓展提高】
(3)如图3,点E在正方形ABCD的边AB上,以CB为直径的圆与CE交于点F,若=,求的值.
浙江省中考数学考前冲刺每日一练35(精选全省各市历年经典真题,包含常考题型、易错题型、 小压轴、大压轴)参考答案与试题解析
一.选择题(共1小题)
1.由新型肺炎疫情影响,各类消毒液需求量大增,卫健委积极推动部分消毒液紧急上市,有效缓解消毒液供需矛盾.根据商场调查,某种消毒液的大瓶装(5kg)和小瓶装(2.5kg)两种产品的销售数量(按瓶计算)比为3:4.某厂每天生产这种消毒液25t,这些消毒液应该分装大、小瓶两种产品各多少瓶?设这些消毒液应该分装x大瓶、y小瓶.根据题意可列方程组( )
A.
B.
C.
D.
【分析】设应该分装大小瓶两种产品x瓶、y瓶,根据大瓶装(500g)和小瓶装(250g)两种产品的销售数量比为3:4,每天生产这种消毒液3:4列方程组成方程组即可.
【解答】解:设这些消毒液应该分装x大瓶、y小瓶.由题意得,.
故选:D.
【点评】此题考查列二元一次方程组解决实际问题,注意题目蕴含的数量关系,正确列式解答即可.
二.填空题(共1小题)
2.如图,在平面直角坐标系中,一次函数y=﹣x+2的图象与y轴正半轴、x轴的正半轴分别交于A,B两点,点M是线段AB上的动点,⊙M的半径为1,当⊙M与坐标轴相切时,则MA的长度是 或 .
【分析】求出A、B的坐标,得到OA,OB的长,由勾股定理求出AB的长,当⊙M与y轴相切时,由△AHM∽△AOB,得到HM:OB=AM:AB,即可求出AM=;当⊙M与x轴相切时,由△BMK∽△BAO,得到KM:AO=BM:AB,求出BM的长,即可得到AM的长,于是得到MA的长度.
【解答】解:当x=0时,y=2,
∴A的坐标是(0,2),
∴OA=2,
当y=0时,0=﹣x+2,得到x=4,
∴B的坐标是(4,0),
∴OB=4,
∴AB==2,
当⊙M与y轴相切时,切点是H,
连接MH,
∴MH⊥AO,
∵BO⊥AO,
∴MH∥BO,
∴△AHM∽△AOB,
∴HM:OB=AM:AB,
∵⊙M的半径为1,
∴MH=1,
∴1:4=AM:2,
∴AM=;
当⊙M与x轴相切时,切点是K,
连接MK,
∴MK⊥OB,
∵AO⊥OB,
∴MK∥AO,
∴△BMK∽△BAO,
∴KM:AO=BM:AB,
∴1:2=BM:2,
∴MB=,
∴AM=AB﹣BM=2﹣=,
∴MA的长度是或.
故答案为:或.
【点评】本题考查切线的性质,相似三角形的判定和性质,一次函数的性质,一次函数图象上坐标的特征,关键是要分两种情况讨论.
三.解答题(共3小题)
3.已知抛物线y=x2﹣2x+c(c是常数)经过点A(﹣1,0).
(1)求该抛物线解析式;
(2)当0<x<3时,求y的取值范围;
(3)若P(a,b)为抛物线上的个动点,P关于原点的对称点为P',当点P′落在该抛物线上时,求a的值.
【分析】(1)根据抛物线y=x2﹣2x+c(c是常数)经过点A(﹣1,0),可以求得c的值,从而可以得到抛物线的解析式;
(2)根据二次函数的性质,可以得到当0<x<3时,y的取值范围;
(3)根据P(m,t)为抛物线上的一个动点,P关于原点的对称点为P′,点P′落在该抛物线上.可以求得a的值.
【解答】解:(1)∵抛物线y=x2﹣2x+c(c是常数)经过点A(﹣1,0),
∴0=1+2+c,
解得c=﹣3,
∴抛物线解析式为y=x2﹣2x﹣3;
(2)∵y=x2﹣2x﹣3=(x﹣1)2﹣4,
∴该抛物线的开口方向向上,对称轴是直线x=1,顶点坐标为(1,﹣4),
∴x=1时,函数有最小值﹣4,
∵当x=0时,y=﹣3,当x=3时,y=x2﹣2x﹣3=0,
∴当0<x<3时,y的取值范围是﹣4≤y<0;
(3)∵P(a,b)为抛物线上的个动点,P关于原点的对称点为P',
∴点P′的坐标为(﹣a,﹣b),
又∵P′落在该抛物线上,
∴,
解得或,
即a的值是或﹣.
【点评】本题考查了二次函数图象上点的坐标特征、待定系数法求二次函数的解析式,二次函数的性质、关于原点对称的点的坐标,解答本题的关键是明确题意,利用二次函数的性质解答.
4.为了解某校九年级学生的理化实验操作情况,随机抽查了40名同学实验操作的得分.根据获取的样本数据,制作了如下的条形统计图和扇形统计图.请根据相关信息,解答下列问题:
(Ⅰ)扇形 ①的圆心角的大小是 36° ;
(Ⅱ)求这40个样本数据的平均数、众数、中位数;
(Ⅲ)若该校九年级共有320名学生,估计该校理化实验操作得满分(10分)有多少人.
【分析】(Ⅰ)用360°乘以①所占的百分比,计算即可得解;
(Ⅱ)根据平均数的定义;众数是一组数据中出现次数最多的数据,注意众数可以不止一个;找中位数要把数据按从小到大的顺序排列,位于最中间的一个数(或两个数的平均数)为中位数分别解答;
(Ⅲ)用九年级总人数乘以满分的人数所占的份数计算即可得解.
【解答】解:(Ⅰ)360°×(1﹣15%﹣27.5%﹣30%﹣17.5%)
=360°×10%
=36°;
故答案为:36°.
(Ⅱ)∵==8.3,
∴平均数是8.3;
∵9出现了12次,次数最多,
∴众数是9;
∵将40个数字按从小到大排列,中间的两个数都是8,
∴中位数是=8;
(Ⅲ)∵320×=56(人),
∴满分约有56人.
【点评】本题属于基础题,考查了确定一组数据的中位数和众数的能力.一些学生往往对这个概念掌握不清楚,计算方法不明确而误选其它选项,注意找中位数的时候一定要先排好顺序,然后再根据奇数和偶数个来确定中位数,如果数据有奇数个,则正中间的数字即为所求,如果是偶数个则找中间两位数的平均数.
5.【基础巩固】
(1)如图1,在Rt△ABC中,∠BAC=90°,AD⊥BC于点D,求证:AD2=BD CD.
【尝试应用】
(2)如图2,在矩形ABCD中,点E为矩形内一点,∠BEC=90°,EF⊥BC于点F.连接AE,AB=AE,EF=,FC=1,求AB的长.
【拓展提高】
(3)如图3,点E在正方形ABCD的边AB上,以CB为直径的圆与CE交于点F,若=,求的值.
【分析】(1)利用等角的余角相等得到∠B=∠DAC,则可判断Rt△ADB∽Rt△CDA,所以AD:CD=BD:AD,然后根据比例的性质即可得到结论;
(2)证明Rt△EFB∽Rt△CFE,可得EF2=BF CF,可求得BF=5,根据勾股定理求出BE=,过A作AH⊥BE于H,根据等腰三角形的性质得BH=BE=,再证Rt△ABH∽Rt△BEF,根据相似三角形的性质即可求解;
(3)连接BF,由CB为直径可得∠BFC=90°,证明Rt△CFB∽Rt△BFE,根据相似三角形的性质得=,可得BF2=EF CF,设EF=2k,则FC=3k,可得BF=k,根据正方形的性质得AB=CB,即可求解.
【解答】(1)证明:∵AD⊥BC于点D,
∴∠ADB=∠ADC=90°,
∴∠B+∠BAD=90°,
又∵∠BAD+∠DAC=∠BAC=90°,
∴∠B=∠DAC,
∴Rt△ADB∽Rt△CDA,
∴AD:CD=BD:AD,
∴AD2=CD BD;
(2)解:同(1)可得Rt△EFB∽Rt△CFE,
∴EF2=BF CF,
∵EF=,FC=1,
∴BF=5,
∴BE==,
过A作AH⊥BE于H,
∴∠AHB=∠BFE=90°,
∵AB=AE,
∴BH=BE=,
∵四边形ABCD是矩形,
∴∠ABC=90°,
∴∠ABH+∠EBF=∠BEF+∠EBF=90°,
∴∠ABH=∠BEF,
∴Rt△ABH∽Rt△BEF,
∴,即,
∴AB=3;
(3)解:连接BF,
∵CB为直径,
∴∠BFC=90°,
∵四边形ABCD是正方形,
∴∠ABC=90°,
同(1)可得Rt△CFB∽Rt△BFE,
∴=,
∴BF2=EF CF,
∵,
设EF=2k,则FC=3k,
∴BF=k,
∴===,
∵四边形ABCD是正方形,
∴AB=CB,
∴=.
【点评】本题是圆的综合题,考查了正方形性质,等腰三角形性质,相似三角形判定和性质,圆的有关性质等知识,解决问题的关键是作辅助线,构造相似三角形.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
