浙江省中考数学考前冲刺每日一练36(精选全省各市历年经典真题,包含常考题型、易错题型、 小压轴、大压轴)
文档属性
| 名称 | 浙江省中考数学考前冲刺每日一练36(精选全省各市历年经典真题,包含常考题型、易错题型、 小压轴、大压轴) |  | |
| 格式 | doc | ||
| 文件大小 | 350.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-24 09:27:45 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
浙江省中考数学考前冲刺每日一练36(精选全省各市历年经典真题,包含常考题型、易错题型、 小压轴、大压轴)
1.如图,在直角坐标系中,△OAB的顶点为O(0,0),A(4,3),B(3,0),以点O为位似中心,在第三象限内作与△OAB的位似比为的位似图形△OCD,则点A的对应点C的坐标为( )
A.(﹣1,﹣1) B.(﹣1,﹣) C.(﹣,﹣1) D.(﹣2,﹣1)
2.抛物线y=(x+2)2+3的顶点坐标是 .
3.如图,在Rt△ABC中,∠ABC=90°,BC=4,BD⊥AC于点D,E是AB边上一点,BE=BC,过点E作EF⊥AB,交BD延长线于点F.
(1)求证:△ABC≌△FEB;
(2)连接AF,若,求AE的长.
4.(1)计算:;
(2)化简:(x+3)(x﹣3)+x(1﹣x).
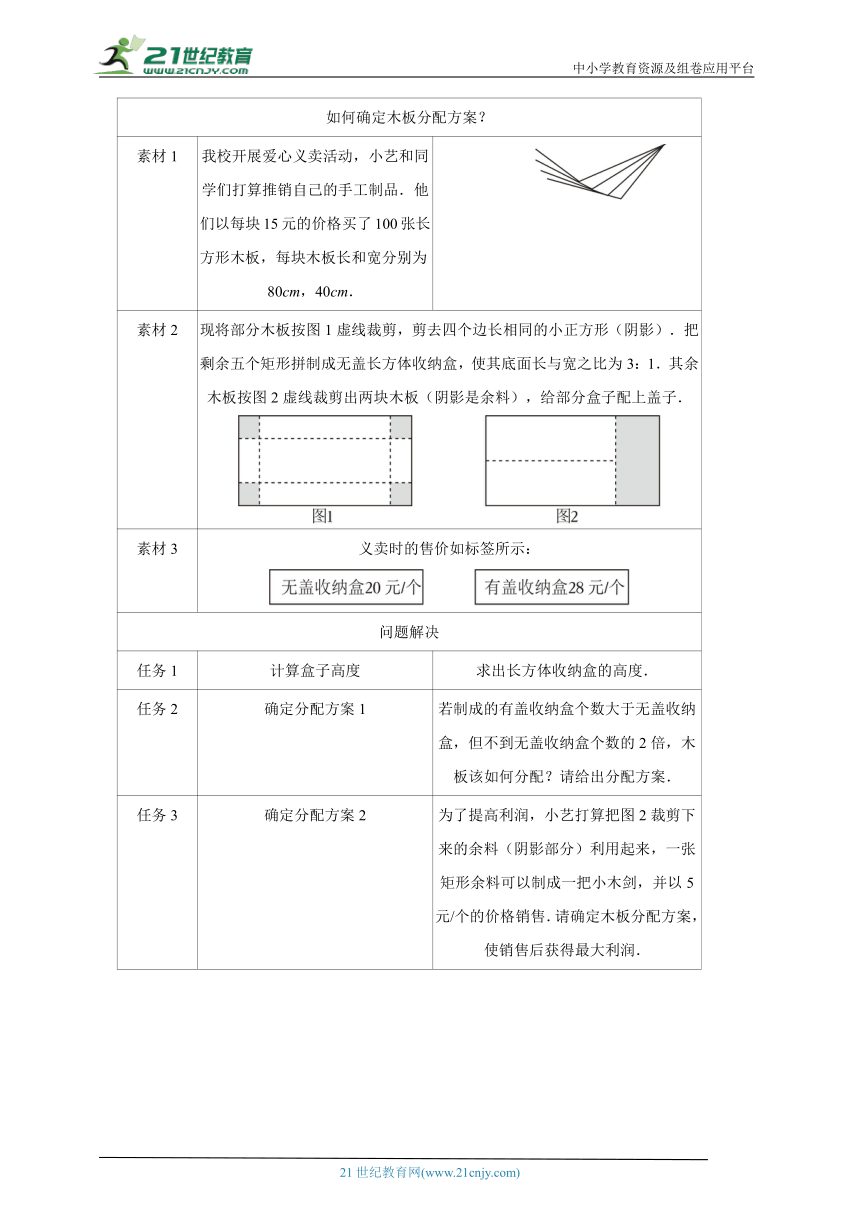
5.根据以下素材,探索完成任务.
如何确定木板分配方案?
素材1 我校开展爱心义卖活动,小艺和同学们打算推销自己的手工制品.他们以每块15元的价格买了100张长方形木板,每块木板长和宽分别为80cm,40cm.
素材2 现将部分木板按图1虚线裁剪,剪去四个边长相同的小正方形(阴影).把剩余五个矩形拼制成无盖长方体收纳盒,使其底面长与宽之比为3:1.其余木板按图2虚线裁剪出两块木板(阴影是余料),给部分盒子配上盖子.
素材3 义卖时的售价如标签所示:
问题解决
任务1 计算盒子高度 求出长方体收纳盒的高度.
任务2 确定分配方案1 若制成的有盖收纳盒个数大于无盖收纳盒,但不到无盖收纳盒个数的2倍,木板该如何分配?请给出分配方案.
任务3 确定分配方案2 为了提高利润,小艺打算把图2裁剪下来的余料(阴影部分)利用起来,一张矩形余料可以制成一把小木剑,并以5元/个的价格销售.请确定木板分配方案,使销售后获得最大利润.
浙江省中考数学考前冲刺每日一练36(精选全省各市历年经典真题,包含常考题型、易错题型、 小压轴、大压轴)参考答案与试题解析
一.选择题(共1小题)
1.如图,在直角坐标系中,△OAB的顶点为O(0,0),A(4,3),B(3,0),以点O为位似中心,在第三象限内作与△OAB的位似比为的位似图形△OCD,则点A的对应点C的坐标为( )
A.(﹣1,﹣1) B.(﹣1,﹣) C.(﹣,﹣1) D.(﹣2,﹣1)
【分析】根据关于以原点为位似中心的对应点的坐标的关系,把A点的横纵坐标都乘以﹣得到C点坐标.
【解答】解:∵△OAB与△OCD为位似图形,点O为位似中心,位似比为,
而A(4,3),
∴点A的对应点C的坐标为(﹣×4,﹣×3),
即C(﹣,﹣1).
故选:C.
【点评】本题考查了位似变换:在平面直角坐标系中,如果位似变换是以原点为位似中心,相似比为k,那么位似图形对应点的坐标的比等于k或﹣k.
二.填空题(共1小题)
2.抛物线y=(x+2)2+3的顶点坐标是 (﹣2,3) .
【分析】已知抛物线解析式为顶点式,可直接写出顶点坐标.
【解答】解:∵y=(x+2)2+3为抛物线的顶点式,根据顶点式的坐标特点可知,
∴抛物线的顶点坐标为(﹣2,3).
故答案为:(﹣2,3).
【点评】本题考查将解析式化为顶点式y=a(x﹣h)2+k,顶点坐标是(h,k),对称轴是直线x=h.
三.解答题(共3小题)
3.如图,在Rt△ABC中,∠ABC=90°,BC=4,BD⊥AC于点D,E是AB边上一点,BE=BC,过点E作EF⊥AB,交BD延长线于点F.
(1)求证:△ABC≌△FEB;
(2)连接AF,若,求AE的长.
【分析】(1)根据题意利用AAS证明△ABC≌△FEB即可;
(2)结合(1)得AB=EF,由BE=BC,得AB=AE+BE=AE+4,利用=,列出等式即可得AE的长.
【解答】(1)证明:∵BD⊥AC,EF⊥AB,
∴∠ADB=∠FEB=90°,
∴∠BAC+∠ABD=∠EFB+∠ABD=90°,
∴∠BAC=∠EFB,
在△ABC和△FEB中,
,
∴△ABC≌△FEB(AAS);
(2)解:∵△ABC≌△FEB,
∴AB=EF,
∵BE=BC=4,
∴AB=AE+BE=AE+4,
∵=,
∴EF=3AE,
∴AE+4=3AE,
∴AE=2.
【点评】本题考查了全等三角形的判定与性质;熟练掌握全等三角形的判定方法证明三角形全等是解决问题的关键.
4.(1)计算:;
(2)化简:(x+3)(x﹣3)+x(1﹣x).
【分析】(1)将代入,将2﹣3转化为,然后再进行计算即可;
(2)先利用平方差公式计算(x+3)(x﹣3)=x2﹣32,再利用单项式乘多项式的法则计算x(1﹣x)=x﹣x2,然后合并同类项即可.
【解答】解:(1)
=
=
=;
(2)原式=x2﹣32+x﹣x2=x﹣9.
【点评】此题主要考查了实数的运算和整式的运算,解答此题的关键熟练掌握特殊角锐角三角函数值:;负整数指数幂的运算法则:(p≠0,且为正整数),以及平方差公式:(a+b)(a﹣b)=a2﹣b2.
5.根据以下素材,探索完成任务.
如何确定木板分配方案?
素材1 我校开展爱心义卖活动,小艺和同学们打算推销自己的手工制品.他们以每块15元的价格买了100张长方形木板,每块木板长和宽分别为80cm,40cm.
素材2 现将部分木板按图1虚线裁剪,剪去四个边长相同的小正方形(阴影).把剩余五个矩形拼制成无盖长方体收纳盒,使其底面长与宽之比为3:1.其余木板按图2虚线裁剪出两块木板(阴影是余料),给部分盒子配上盖子.
素材3 义卖时的售价如标签所示:
问题解决
任务1 计算盒子高度 求出长方体收纳盒的高度.
任务2 确定分配方案1 若制成的有盖收纳盒个数大于无盖收纳盒,但不到无盖收纳盒个数的2倍,木板该如何分配?请给出分配方案.
任务3 确定分配方案2 为了提高利润,小艺打算把图2裁剪下来的余料(阴影部分)利用起来,一张矩形余料可以制成一把小木剑,并以5元/个的价格销售.请确定木板分配方案,使销售后获得最大利润.
【分析】任务1:根据“底面长与宽之比为3:1”列方程求解;
任务2:根据“制成的有盖收纳盒个数大于无盖收纳盒,但不到无盖收纳盒个数的2倍”列不等式组求解;
任务3:根据题意理出函数表达式,再根据函数的性质求解.
【解答】解:任务1:设长方体的高度为a cm,
则:80﹣2a=3(40﹣2a),
解得:a=10,
答:长方体的高度为10cm;
任务2:设x张木板制作无盖的收纳盒,
则:,
解得:75<x<80,
∴x的整数解有:76,77,78,79,
∴共有4种方案:①76张木板制作无盖的收纳盒,24张制作盒盖;
②77张木板制作无盖的收纳盒,23张制作盒盖;
③78张木板制作无盖的收纳盒,22张制作盒盖;
④79张木板制作无盖的收纳盒,21张制作盒盖;
任务3:设:m张木板制作无盖的收纳盒,则(100﹣m)张制作盒盖,利润为y元,
由题意得:y=28×2(100﹣m)+5(100﹣m)+20×[m﹣(100﹣m)]﹣1500
即:y=﹣21m+2600,
∵x的整数解有:76,77,78,79,
∴当m=76时,y有最大值,为:﹣21×76+2600=1004,
答:76张木板制作无盖的收纳盒,23张制作盒盖,利润最大,最大值为1004元.
【点评】本题考查了方程组及不等式组的应用,找出相等关系或不等关系是解题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
浙江省中考数学考前冲刺每日一练36(精选全省各市历年经典真题,包含常考题型、易错题型、 小压轴、大压轴)
1.如图,在直角坐标系中,△OAB的顶点为O(0,0),A(4,3),B(3,0),以点O为位似中心,在第三象限内作与△OAB的位似比为的位似图形△OCD,则点A的对应点C的坐标为( )
A.(﹣1,﹣1) B.(﹣1,﹣) C.(﹣,﹣1) D.(﹣2,﹣1)
2.抛物线y=(x+2)2+3的顶点坐标是 .
3.如图,在Rt△ABC中,∠ABC=90°,BC=4,BD⊥AC于点D,E是AB边上一点,BE=BC,过点E作EF⊥AB,交BD延长线于点F.
(1)求证:△ABC≌△FEB;
(2)连接AF,若,求AE的长.
4.(1)计算:;
(2)化简:(x+3)(x﹣3)+x(1﹣x).
5.根据以下素材,探索完成任务.
如何确定木板分配方案?
素材1 我校开展爱心义卖活动,小艺和同学们打算推销自己的手工制品.他们以每块15元的价格买了100张长方形木板,每块木板长和宽分别为80cm,40cm.
素材2 现将部分木板按图1虚线裁剪,剪去四个边长相同的小正方形(阴影).把剩余五个矩形拼制成无盖长方体收纳盒,使其底面长与宽之比为3:1.其余木板按图2虚线裁剪出两块木板(阴影是余料),给部分盒子配上盖子.
素材3 义卖时的售价如标签所示:
问题解决
任务1 计算盒子高度 求出长方体收纳盒的高度.
任务2 确定分配方案1 若制成的有盖收纳盒个数大于无盖收纳盒,但不到无盖收纳盒个数的2倍,木板该如何分配?请给出分配方案.
任务3 确定分配方案2 为了提高利润,小艺打算把图2裁剪下来的余料(阴影部分)利用起来,一张矩形余料可以制成一把小木剑,并以5元/个的价格销售.请确定木板分配方案,使销售后获得最大利润.
浙江省中考数学考前冲刺每日一练36(精选全省各市历年经典真题,包含常考题型、易错题型、 小压轴、大压轴)参考答案与试题解析
一.选择题(共1小题)
1.如图,在直角坐标系中,△OAB的顶点为O(0,0),A(4,3),B(3,0),以点O为位似中心,在第三象限内作与△OAB的位似比为的位似图形△OCD,则点A的对应点C的坐标为( )
A.(﹣1,﹣1) B.(﹣1,﹣) C.(﹣,﹣1) D.(﹣2,﹣1)
【分析】根据关于以原点为位似中心的对应点的坐标的关系,把A点的横纵坐标都乘以﹣得到C点坐标.
【解答】解:∵△OAB与△OCD为位似图形,点O为位似中心,位似比为,
而A(4,3),
∴点A的对应点C的坐标为(﹣×4,﹣×3),
即C(﹣,﹣1).
故选:C.
【点评】本题考查了位似变换:在平面直角坐标系中,如果位似变换是以原点为位似中心,相似比为k,那么位似图形对应点的坐标的比等于k或﹣k.
二.填空题(共1小题)
2.抛物线y=(x+2)2+3的顶点坐标是 (﹣2,3) .
【分析】已知抛物线解析式为顶点式,可直接写出顶点坐标.
【解答】解:∵y=(x+2)2+3为抛物线的顶点式,根据顶点式的坐标特点可知,
∴抛物线的顶点坐标为(﹣2,3).
故答案为:(﹣2,3).
【点评】本题考查将解析式化为顶点式y=a(x﹣h)2+k,顶点坐标是(h,k),对称轴是直线x=h.
三.解答题(共3小题)
3.如图,在Rt△ABC中,∠ABC=90°,BC=4,BD⊥AC于点D,E是AB边上一点,BE=BC,过点E作EF⊥AB,交BD延长线于点F.
(1)求证:△ABC≌△FEB;
(2)连接AF,若,求AE的长.
【分析】(1)根据题意利用AAS证明△ABC≌△FEB即可;
(2)结合(1)得AB=EF,由BE=BC,得AB=AE+BE=AE+4,利用=,列出等式即可得AE的长.
【解答】(1)证明:∵BD⊥AC,EF⊥AB,
∴∠ADB=∠FEB=90°,
∴∠BAC+∠ABD=∠EFB+∠ABD=90°,
∴∠BAC=∠EFB,
在△ABC和△FEB中,
,
∴△ABC≌△FEB(AAS);
(2)解:∵△ABC≌△FEB,
∴AB=EF,
∵BE=BC=4,
∴AB=AE+BE=AE+4,
∵=,
∴EF=3AE,
∴AE+4=3AE,
∴AE=2.
【点评】本题考查了全等三角形的判定与性质;熟练掌握全等三角形的判定方法证明三角形全等是解决问题的关键.
4.(1)计算:;
(2)化简:(x+3)(x﹣3)+x(1﹣x).
【分析】(1)将代入,将2﹣3转化为,然后再进行计算即可;
(2)先利用平方差公式计算(x+3)(x﹣3)=x2﹣32,再利用单项式乘多项式的法则计算x(1﹣x)=x﹣x2,然后合并同类项即可.
【解答】解:(1)
=
=
=;
(2)原式=x2﹣32+x﹣x2=x﹣9.
【点评】此题主要考查了实数的运算和整式的运算,解答此题的关键熟练掌握特殊角锐角三角函数值:;负整数指数幂的运算法则:(p≠0,且为正整数),以及平方差公式:(a+b)(a﹣b)=a2﹣b2.
5.根据以下素材,探索完成任务.
如何确定木板分配方案?
素材1 我校开展爱心义卖活动,小艺和同学们打算推销自己的手工制品.他们以每块15元的价格买了100张长方形木板,每块木板长和宽分别为80cm,40cm.
素材2 现将部分木板按图1虚线裁剪,剪去四个边长相同的小正方形(阴影).把剩余五个矩形拼制成无盖长方体收纳盒,使其底面长与宽之比为3:1.其余木板按图2虚线裁剪出两块木板(阴影是余料),给部分盒子配上盖子.
素材3 义卖时的售价如标签所示:
问题解决
任务1 计算盒子高度 求出长方体收纳盒的高度.
任务2 确定分配方案1 若制成的有盖收纳盒个数大于无盖收纳盒,但不到无盖收纳盒个数的2倍,木板该如何分配?请给出分配方案.
任务3 确定分配方案2 为了提高利润,小艺打算把图2裁剪下来的余料(阴影部分)利用起来,一张矩形余料可以制成一把小木剑,并以5元/个的价格销售.请确定木板分配方案,使销售后获得最大利润.
【分析】任务1:根据“底面长与宽之比为3:1”列方程求解;
任务2:根据“制成的有盖收纳盒个数大于无盖收纳盒,但不到无盖收纳盒个数的2倍”列不等式组求解;
任务3:根据题意理出函数表达式,再根据函数的性质求解.
【解答】解:任务1:设长方体的高度为a cm,
则:80﹣2a=3(40﹣2a),
解得:a=10,
答:长方体的高度为10cm;
任务2:设x张木板制作无盖的收纳盒,
则:,
解得:75<x<80,
∴x的整数解有:76,77,78,79,
∴共有4种方案:①76张木板制作无盖的收纳盒,24张制作盒盖;
②77张木板制作无盖的收纳盒,23张制作盒盖;
③78张木板制作无盖的收纳盒,22张制作盒盖;
④79张木板制作无盖的收纳盒,21张制作盒盖;
任务3:设:m张木板制作无盖的收纳盒,则(100﹣m)张制作盒盖,利润为y元,
由题意得:y=28×2(100﹣m)+5(100﹣m)+20×[m﹣(100﹣m)]﹣1500
即:y=﹣21m+2600,
∵x的整数解有:76,77,78,79,
∴当m=76时,y有最大值,为:﹣21×76+2600=1004,
答:76张木板制作无盖的收纳盒,23张制作盒盖,利润最大,最大值为1004元.
【点评】本题考查了方程组及不等式组的应用,找出相等关系或不等关系是解题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
