浙江省中考数学考前冲刺每日一练37(精选全省各市历年经典真题,包含常考题型、易错题型、 小压轴、大压轴)
文档属性
| 名称 | 浙江省中考数学考前冲刺每日一练37(精选全省各市历年经典真题,包含常考题型、易错题型、 小压轴、大压轴) | 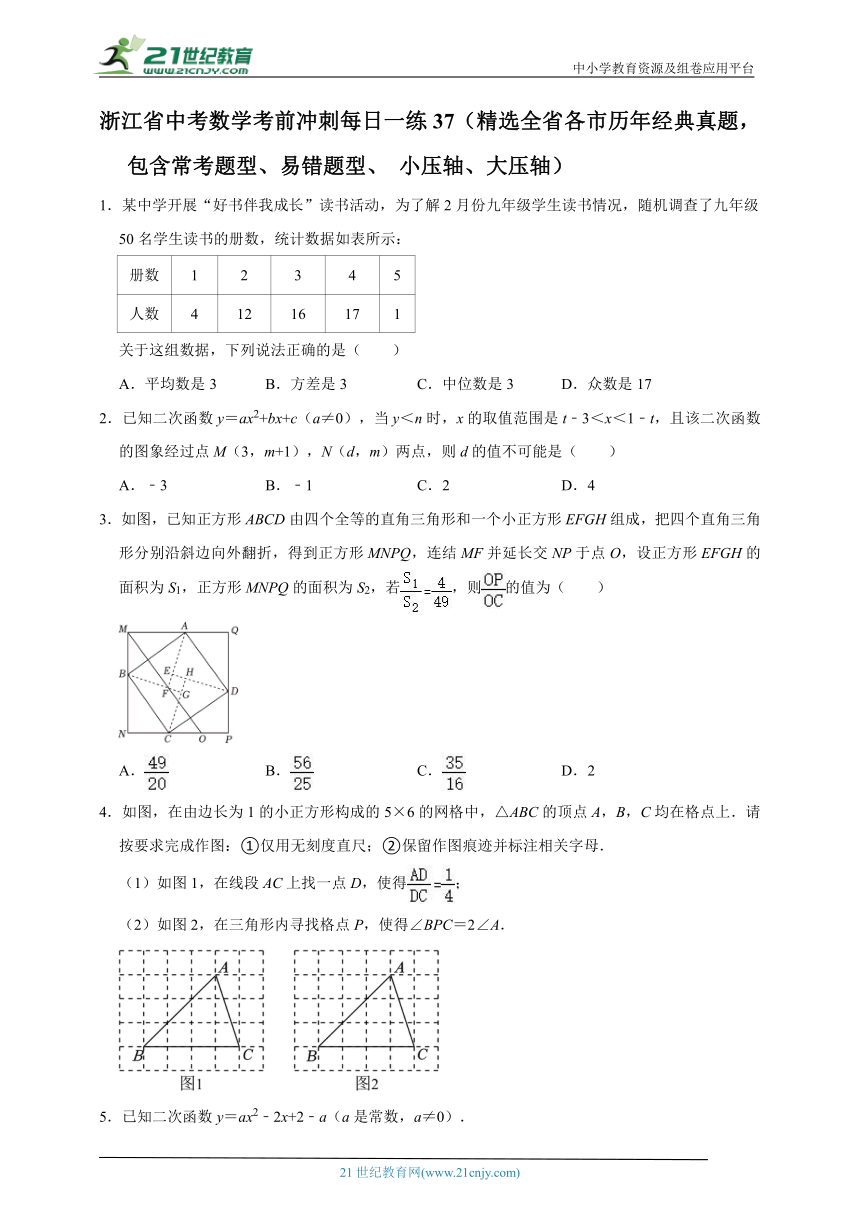 | |
| 格式 | doc | ||
| 文件大小 | 381.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-24 09:27:45 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
浙江省中考数学考前冲刺每日一练37(精选全省各市历年经典真题,包含常考题型、易错题型、 小压轴、大压轴)
1.某中学开展“好书伴我成长”读书活动,为了解2月份九年级学生读书情况,随机调查了九年级50名学生读书的册数,统计数据如表所示:
册数 1 2 3 4 5
人数 4 12 16 17 1
关于这组数据,下列说法正确的是( )
A.平均数是3 B.方差是3 C.中位数是3 D.众数是17
2.已知二次函数y=ax2+bx+c(a≠0),当y<n时,x的取值范围是t﹣3<x<1﹣t,且该二次函数的图象经过点M(3,m+1),N(d,m)两点,则d的值不可能是( )
A.﹣3 B.﹣1 C.2 D.4
3.如图,已知正方形ABCD由四个全等的直角三角形和一个小正方形EFGH组成,把四个直角三角形分别沿斜边向外翻折,得到正方形MNPQ,连结MF并延长交NP于点O,设正方形EFGH的面积为S1,正方形MNPQ的面积为S2,若,则的值为( )
A. B. C. D.2
4.如图,在由边长为1的小正方形构成的5×6的网格中,△ABC的顶点A,B,C均在格点上.请按要求完成作图:①仅用无刻度直尺;②保留作图痕迹并标注相关字母.
(1)如图1,在线段AC上找一点D,使得;
(2)如图2,在三角形内寻找格点P,使得∠BPC=2∠A.
5.已知二次函数y=ax2﹣2x+2﹣a(a是常数,a≠0).
(1)若a=﹣,求该函数图象顶点坐标.
(2)若该二次函数图象经过(﹣1,1),(1,﹣2),(2,﹣5)三个点中的一个点,求该二次函数的表达式.
(3)若﹣5≤a≤﹣2,当﹣3≤x≤0时,y=ax2﹣2x+2﹣a的最大值记为m,最小值记为n,求am﹣n的最小值.
浙江省中考数学考前冲刺每日一练37(精选全省各市历年经典真题,包含常考题型、易错题型、 小压轴、大压轴)参考答案与试题解析
一.选择题(共3小题)
1.某中学开展“好书伴我成长”读书活动,为了解2月份九年级学生读书情况,随机调查了九年级50名学生读书的册数,统计数据如表所示:
册数 1 2 3 4 5
人数 4 12 16 17 1
关于这组数据,下列说法正确的是( )
A.平均数是3 B.方差是3 C.中位数是3 D.众数是17
【分析】先根据表格提示的数据得出50名学生读书的册数,然后除以50即可求出平均数;在这组样本数据中,3出现的次数最多,所以求出了众数;将这组样本数据按从小到大的顺序排列,其中处于中间的两个数都是2,从而求出中位数是2,根据方差公式即可得出答案.
【解答】解:观察表格,可知这组样本数据的平均数为:
(1×4+2×12+3×16+4×17+5×1)÷50=2.98;
∵这组样本数据中,3出现了17次,出现的次数最多,
∴这组数据的众数是3;
∵将这组样本数据按从小到大的顺序排列,其中处于中间的两个数都是3,
∴这组数据的中位数为3,
∵这组样本数据的平均数为2.98,
∴这组样本数据的方差不是整数.
故选:C.
【点评】本题考查的知识点有:用样本估计总体、众数、方差以及中位数的知识,解题的关键是牢记概念及公式.
2.已知二次函数y=ax2+bx+c(a≠0),当y<n时,x的取值范围是t﹣3<x<1﹣t,且该二次函数的图象经过点M(3,m+1),N(d,m)两点,则d的值不可能是( )
A.﹣3 B.﹣1 C.2 D.4
【分析】根据y<n时,x的取值范围是t﹣3<x<1﹣t,可得抛物线图象开口方向及对称轴直线方程,再根据二次函数的性质进而求解.
【解答】解:如图,
∵二次函数y=ax2+bx+c(a≠0),当y<n时,x的取值范围是t﹣3<x<1﹣t,
∴二次函数开口向上,对称轴为直线x=﹣1,
∵该二次函数的图象经过点M(3,m+1),N(d,m)两点,
∴点M(3,m+1)关于对称轴的对称点为(﹣5,m+1),
∴﹣5<d<3,
∴d不可能是4.
故选:D.
【点评】本题考查二次函数的性质,解题关键是熟练掌握二次函数的性质,结合图象求解.
3.如图,已知正方形ABCD由四个全等的直角三角形和一个小正方形EFGH组成,把四个直角三角形分别沿斜边向外翻折,得到正方形MNPQ,连结MF并延长交NP于点O,设正方形EFGH的面积为S1,正方形MNPQ的面积为S2,若,则的值为( )
A. B. C. D.2
【分析】根据,设S1=4k2,S2=49k2,则正方形EFGH边长为2k,正方形MNPQ的边长为7k,即FG=2k,NP=7k,设NC=a,PC=b,依题意得BF=CG=NC=BM=a,BG=BN=CP=b,则,解得,则NC=BM=2.5k,CP=4.5k,证BC∥MO,得△BNC∽△MNO,则BN:MN=NC:NO,即4.5k:7k=2.5k:NO,由此得NO=,则OC=NO﹣NC=,进而得OP=CP﹣OC=,据此可得的值.
【解答】解:,
∴设S1=4k2,S2=49k2,
∴正方形EFGH边长为2k,正方形MNPQ的边长为7k,
即FG=2k,MN=NP=7k,
设NC=a,PC=b,
依题意得:△AMB,△AFB,△BNC,△BGC,△CPD,△XHD,△DQA,△DEA都全等,
∴BF=CG=NC=BM=a,BG=BN=CP=b,
∴BG﹣BF=FG,NC+CP=NP,
∴,解得,
∴NC=BM=2.5k,CP=4.5k,
∵AM=AF,
∴点A在线段AF的垂直平分线上,
∴BF=BM,
∴点B在线段AF的垂直平分线上,
∴AB是线段AF的垂直平分线,
即AB⊥MO,
又∵四边形ABCD为正方形,
∴∠ABC=90°,
∴BC∥MO,
∴△BNC∽△MNO,
∴BN:MN=NC:NO,
即4.5k:7k=2.5k:NO,
∴NO=,
∴OC=NO﹣NC=﹣2.5k=,
∴OP=CP﹣OC=4.5k﹣=,
∴=.
故选:B.
【点评】此题主要考查了正方形的性质,全等三角形的判定和性质,相似三角形的判定和性质,理解正方形的性质,全等三角形的判定和性质,熟练掌握相似三角形的判定和性质是解决问题的关键.
二.解答题(共2小题)
4.如图,在由边长为1的小正方形构成的5×6的网格中,△ABC的顶点A,B,C均在格点上.请按要求完成作图:①仅用无刻度直尺;②保留作图痕迹并标注相关字母.
(1)如图1,在线段AC上找一点D,使得;
(2)如图2,在三角形内寻找格点P,使得∠BPC=2∠A.
【分析】(1)分别取格点M,N,使AM:CN=1:4,且AM∥CN,连接MN,交AC于点D,结合相似三角形的判定与性质可知,点D即为所求.
(2)分别作线段BC,AC的垂直平分线,相交于点P,结合线段垂直平分线的性质、三角形外角的性质可知,点P即为所求.
【解答】解:(1)如图1,分别取格点M,N,使AM:CN=1:4,且AM∥CN,连接MN,交AC于点D,
则△ADM∽△CDN,
∴=,
则点D即为所求.
(2)如图2,分别作线段BC,AC的垂直平分线,相交于点P,
连接BP并延长,交格点于点D,连接CP并延长,交格点于点E,
则∠ABP=∠BAP,∠ACP=∠CAP,
∴∠APD=∠ABP+∠BAP=2∠BAP,∠APE=∠ACP+∠CAP=2∠CAP,
∴∠DPE=∠APD+∠APE=2(∠BAP+∠CAP)=2∠BAC,
∴∠BPC=∠DPE=2∠BAC,
则点P即为所求.
【点评】本题考查作图—应用与设计作图、相似三角形的判定与性质、线段垂直平分线的性质、三角形外角的性质,解题的关键是理解题意,灵活运用所学知识解决问题.
5.已知二次函数y=ax2﹣2x+2﹣a(a是常数,a≠0).
(1)若a=﹣,求该函数图象顶点坐标.
(2)若该二次函数图象经过(﹣1,1),(1,﹣2),(2,﹣5)三个点中的一个点,求该二次函数的表达式.
(3)若﹣5≤a≤﹣2,当﹣3≤x≤0时,y=ax2﹣2x+2﹣a的最大值记为m,最小值记为n,求am﹣n的最小值.
【分析】(1)当a=﹣时,二次函数y=﹣x2﹣2x+,化成顶点式即可求出顶点坐标;
(2)先判断抛物线过点(2,﹣5),代入解析式即可求得a=﹣1,从而求得抛物线的解析式;
(3)二次函数y=ax2﹣2x+2﹣a,由﹣5≤a≤﹣2得出﹣≤≤﹣,抛物线开口向下,即可得出x=时,y=m,x=﹣3时,y=n,进而得出am﹣n=﹣a2+2a﹣1﹣8a﹣8=﹣a2﹣6a﹣9=﹣(a+3)2,根据﹣5≤a≤﹣2求得最小值为﹣4.
【解答】解:(1)当a=﹣时,二次函数y=﹣x2﹣2x+=﹣(x+2)2+,
∴顶点坐标为(﹣2,);
(2)∵y=ax2﹣2x+2﹣a
=a(x2﹣1)﹣2(x﹣1)
=a(x+1)(x﹣1)﹣2(x﹣1)
=(x﹣1)(ax+a﹣2),
当x=1时,y=0≠﹣2,因此不过(1,﹣2)点,
当x=﹣1时,y=4≠1,因此不过(﹣1,1)点,
故抛物线过点(2,﹣5),代入得,4a﹣4+2﹣a=﹣5,
∴a=﹣1,
∴抛物线的关系式为y=﹣x2﹣2x+3;
(3)∵二次函数y=ax2﹣2x+2﹣a,
∴对称轴为直线x=,
∵﹣5≤a≤﹣2,
∴﹣≤≤﹣,抛物线开口向下,
∵﹣3≤x≤0时,y=ax2﹣2x+2﹣a的最大值记为m,最小值记为n,
∴x=时,y=m,x=﹣3时,y=n,
∴m=﹣+2﹣a=2﹣a﹣,n=9a+6+2﹣a=8a+8,
∴am=﹣a2+2a﹣1,
∴am﹣n=﹣a2+2a﹣1﹣8a﹣8=﹣a2﹣6a﹣9=﹣(a+3)2,
∵﹣5≤a≤﹣2,
∴当a=﹣5时,am﹣n有最小值,为﹣4.
【点评】本题是主要考查了二次函数的图象与性质,二次函数图象上点的坐标特征,关键是根据题意用关于a的式子表示出m、n.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
浙江省中考数学考前冲刺每日一练37(精选全省各市历年经典真题,包含常考题型、易错题型、 小压轴、大压轴)
1.某中学开展“好书伴我成长”读书活动,为了解2月份九年级学生读书情况,随机调查了九年级50名学生读书的册数,统计数据如表所示:
册数 1 2 3 4 5
人数 4 12 16 17 1
关于这组数据,下列说法正确的是( )
A.平均数是3 B.方差是3 C.中位数是3 D.众数是17
2.已知二次函数y=ax2+bx+c(a≠0),当y<n时,x的取值范围是t﹣3<x<1﹣t,且该二次函数的图象经过点M(3,m+1),N(d,m)两点,则d的值不可能是( )
A.﹣3 B.﹣1 C.2 D.4
3.如图,已知正方形ABCD由四个全等的直角三角形和一个小正方形EFGH组成,把四个直角三角形分别沿斜边向外翻折,得到正方形MNPQ,连结MF并延长交NP于点O,设正方形EFGH的面积为S1,正方形MNPQ的面积为S2,若,则的值为( )
A. B. C. D.2
4.如图,在由边长为1的小正方形构成的5×6的网格中,△ABC的顶点A,B,C均在格点上.请按要求完成作图:①仅用无刻度直尺;②保留作图痕迹并标注相关字母.
(1)如图1,在线段AC上找一点D,使得;
(2)如图2,在三角形内寻找格点P,使得∠BPC=2∠A.
5.已知二次函数y=ax2﹣2x+2﹣a(a是常数,a≠0).
(1)若a=﹣,求该函数图象顶点坐标.
(2)若该二次函数图象经过(﹣1,1),(1,﹣2),(2,﹣5)三个点中的一个点,求该二次函数的表达式.
(3)若﹣5≤a≤﹣2,当﹣3≤x≤0时,y=ax2﹣2x+2﹣a的最大值记为m,最小值记为n,求am﹣n的最小值.
浙江省中考数学考前冲刺每日一练37(精选全省各市历年经典真题,包含常考题型、易错题型、 小压轴、大压轴)参考答案与试题解析
一.选择题(共3小题)
1.某中学开展“好书伴我成长”读书活动,为了解2月份九年级学生读书情况,随机调查了九年级50名学生读书的册数,统计数据如表所示:
册数 1 2 3 4 5
人数 4 12 16 17 1
关于这组数据,下列说法正确的是( )
A.平均数是3 B.方差是3 C.中位数是3 D.众数是17
【分析】先根据表格提示的数据得出50名学生读书的册数,然后除以50即可求出平均数;在这组样本数据中,3出现的次数最多,所以求出了众数;将这组样本数据按从小到大的顺序排列,其中处于中间的两个数都是2,从而求出中位数是2,根据方差公式即可得出答案.
【解答】解:观察表格,可知这组样本数据的平均数为:
(1×4+2×12+3×16+4×17+5×1)÷50=2.98;
∵这组样本数据中,3出现了17次,出现的次数最多,
∴这组数据的众数是3;
∵将这组样本数据按从小到大的顺序排列,其中处于中间的两个数都是3,
∴这组数据的中位数为3,
∵这组样本数据的平均数为2.98,
∴这组样本数据的方差不是整数.
故选:C.
【点评】本题考查的知识点有:用样本估计总体、众数、方差以及中位数的知识,解题的关键是牢记概念及公式.
2.已知二次函数y=ax2+bx+c(a≠0),当y<n时,x的取值范围是t﹣3<x<1﹣t,且该二次函数的图象经过点M(3,m+1),N(d,m)两点,则d的值不可能是( )
A.﹣3 B.﹣1 C.2 D.4
【分析】根据y<n时,x的取值范围是t﹣3<x<1﹣t,可得抛物线图象开口方向及对称轴直线方程,再根据二次函数的性质进而求解.
【解答】解:如图,
∵二次函数y=ax2+bx+c(a≠0),当y<n时,x的取值范围是t﹣3<x<1﹣t,
∴二次函数开口向上,对称轴为直线x=﹣1,
∵该二次函数的图象经过点M(3,m+1),N(d,m)两点,
∴点M(3,m+1)关于对称轴的对称点为(﹣5,m+1),
∴﹣5<d<3,
∴d不可能是4.
故选:D.
【点评】本题考查二次函数的性质,解题关键是熟练掌握二次函数的性质,结合图象求解.
3.如图,已知正方形ABCD由四个全等的直角三角形和一个小正方形EFGH组成,把四个直角三角形分别沿斜边向外翻折,得到正方形MNPQ,连结MF并延长交NP于点O,设正方形EFGH的面积为S1,正方形MNPQ的面积为S2,若,则的值为( )
A. B. C. D.2
【分析】根据,设S1=4k2,S2=49k2,则正方形EFGH边长为2k,正方形MNPQ的边长为7k,即FG=2k,NP=7k,设NC=a,PC=b,依题意得BF=CG=NC=BM=a,BG=BN=CP=b,则,解得,则NC=BM=2.5k,CP=4.5k,证BC∥MO,得△BNC∽△MNO,则BN:MN=NC:NO,即4.5k:7k=2.5k:NO,由此得NO=,则OC=NO﹣NC=,进而得OP=CP﹣OC=,据此可得的值.
【解答】解:,
∴设S1=4k2,S2=49k2,
∴正方形EFGH边长为2k,正方形MNPQ的边长为7k,
即FG=2k,MN=NP=7k,
设NC=a,PC=b,
依题意得:△AMB,△AFB,△BNC,△BGC,△CPD,△XHD,△DQA,△DEA都全等,
∴BF=CG=NC=BM=a,BG=BN=CP=b,
∴BG﹣BF=FG,NC+CP=NP,
∴,解得,
∴NC=BM=2.5k,CP=4.5k,
∵AM=AF,
∴点A在线段AF的垂直平分线上,
∴BF=BM,
∴点B在线段AF的垂直平分线上,
∴AB是线段AF的垂直平分线,
即AB⊥MO,
又∵四边形ABCD为正方形,
∴∠ABC=90°,
∴BC∥MO,
∴△BNC∽△MNO,
∴BN:MN=NC:NO,
即4.5k:7k=2.5k:NO,
∴NO=,
∴OC=NO﹣NC=﹣2.5k=,
∴OP=CP﹣OC=4.5k﹣=,
∴=.
故选:B.
【点评】此题主要考查了正方形的性质,全等三角形的判定和性质,相似三角形的判定和性质,理解正方形的性质,全等三角形的判定和性质,熟练掌握相似三角形的判定和性质是解决问题的关键.
二.解答题(共2小题)
4.如图,在由边长为1的小正方形构成的5×6的网格中,△ABC的顶点A,B,C均在格点上.请按要求完成作图:①仅用无刻度直尺;②保留作图痕迹并标注相关字母.
(1)如图1,在线段AC上找一点D,使得;
(2)如图2,在三角形内寻找格点P,使得∠BPC=2∠A.
【分析】(1)分别取格点M,N,使AM:CN=1:4,且AM∥CN,连接MN,交AC于点D,结合相似三角形的判定与性质可知,点D即为所求.
(2)分别作线段BC,AC的垂直平分线,相交于点P,结合线段垂直平分线的性质、三角形外角的性质可知,点P即为所求.
【解答】解:(1)如图1,分别取格点M,N,使AM:CN=1:4,且AM∥CN,连接MN,交AC于点D,
则△ADM∽△CDN,
∴=,
则点D即为所求.
(2)如图2,分别作线段BC,AC的垂直平分线,相交于点P,
连接BP并延长,交格点于点D,连接CP并延长,交格点于点E,
则∠ABP=∠BAP,∠ACP=∠CAP,
∴∠APD=∠ABP+∠BAP=2∠BAP,∠APE=∠ACP+∠CAP=2∠CAP,
∴∠DPE=∠APD+∠APE=2(∠BAP+∠CAP)=2∠BAC,
∴∠BPC=∠DPE=2∠BAC,
则点P即为所求.
【点评】本题考查作图—应用与设计作图、相似三角形的判定与性质、线段垂直平分线的性质、三角形外角的性质,解题的关键是理解题意,灵活运用所学知识解决问题.
5.已知二次函数y=ax2﹣2x+2﹣a(a是常数,a≠0).
(1)若a=﹣,求该函数图象顶点坐标.
(2)若该二次函数图象经过(﹣1,1),(1,﹣2),(2,﹣5)三个点中的一个点,求该二次函数的表达式.
(3)若﹣5≤a≤﹣2,当﹣3≤x≤0时,y=ax2﹣2x+2﹣a的最大值记为m,最小值记为n,求am﹣n的最小值.
【分析】(1)当a=﹣时,二次函数y=﹣x2﹣2x+,化成顶点式即可求出顶点坐标;
(2)先判断抛物线过点(2,﹣5),代入解析式即可求得a=﹣1,从而求得抛物线的解析式;
(3)二次函数y=ax2﹣2x+2﹣a,由﹣5≤a≤﹣2得出﹣≤≤﹣,抛物线开口向下,即可得出x=时,y=m,x=﹣3时,y=n,进而得出am﹣n=﹣a2+2a﹣1﹣8a﹣8=﹣a2﹣6a﹣9=﹣(a+3)2,根据﹣5≤a≤﹣2求得最小值为﹣4.
【解答】解:(1)当a=﹣时,二次函数y=﹣x2﹣2x+=﹣(x+2)2+,
∴顶点坐标为(﹣2,);
(2)∵y=ax2﹣2x+2﹣a
=a(x2﹣1)﹣2(x﹣1)
=a(x+1)(x﹣1)﹣2(x﹣1)
=(x﹣1)(ax+a﹣2),
当x=1时,y=0≠﹣2,因此不过(1,﹣2)点,
当x=﹣1时,y=4≠1,因此不过(﹣1,1)点,
故抛物线过点(2,﹣5),代入得,4a﹣4+2﹣a=﹣5,
∴a=﹣1,
∴抛物线的关系式为y=﹣x2﹣2x+3;
(3)∵二次函数y=ax2﹣2x+2﹣a,
∴对称轴为直线x=,
∵﹣5≤a≤﹣2,
∴﹣≤≤﹣,抛物线开口向下,
∵﹣3≤x≤0时,y=ax2﹣2x+2﹣a的最大值记为m,最小值记为n,
∴x=时,y=m,x=﹣3时,y=n,
∴m=﹣+2﹣a=2﹣a﹣,n=9a+6+2﹣a=8a+8,
∴am=﹣a2+2a﹣1,
∴am﹣n=﹣a2+2a﹣1﹣8a﹣8=﹣a2﹣6a﹣9=﹣(a+3)2,
∵﹣5≤a≤﹣2,
∴当a=﹣5时,am﹣n有最小值,为﹣4.
【点评】本题是主要考查了二次函数的图象与性质,二次函数图象上点的坐标特征,关键是根据题意用关于a的式子表示出m、n.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
