浙江省中考数学考前冲刺每日一练38(精选全省各市历年经典真题,包含常考题型、易错题型、 小压轴、大压轴)
文档属性
| 名称 | 浙江省中考数学考前冲刺每日一练38(精选全省各市历年经典真题,包含常考题型、易错题型、 小压轴、大压轴) |  | |
| 格式 | doc | ||
| 文件大小 | 517.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-24 09:27:45 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
浙江省中考数学考前冲刺每日一练38(精选全省各市历年经典真题,包含常考题型、易错题型、 小压轴、大压轴)
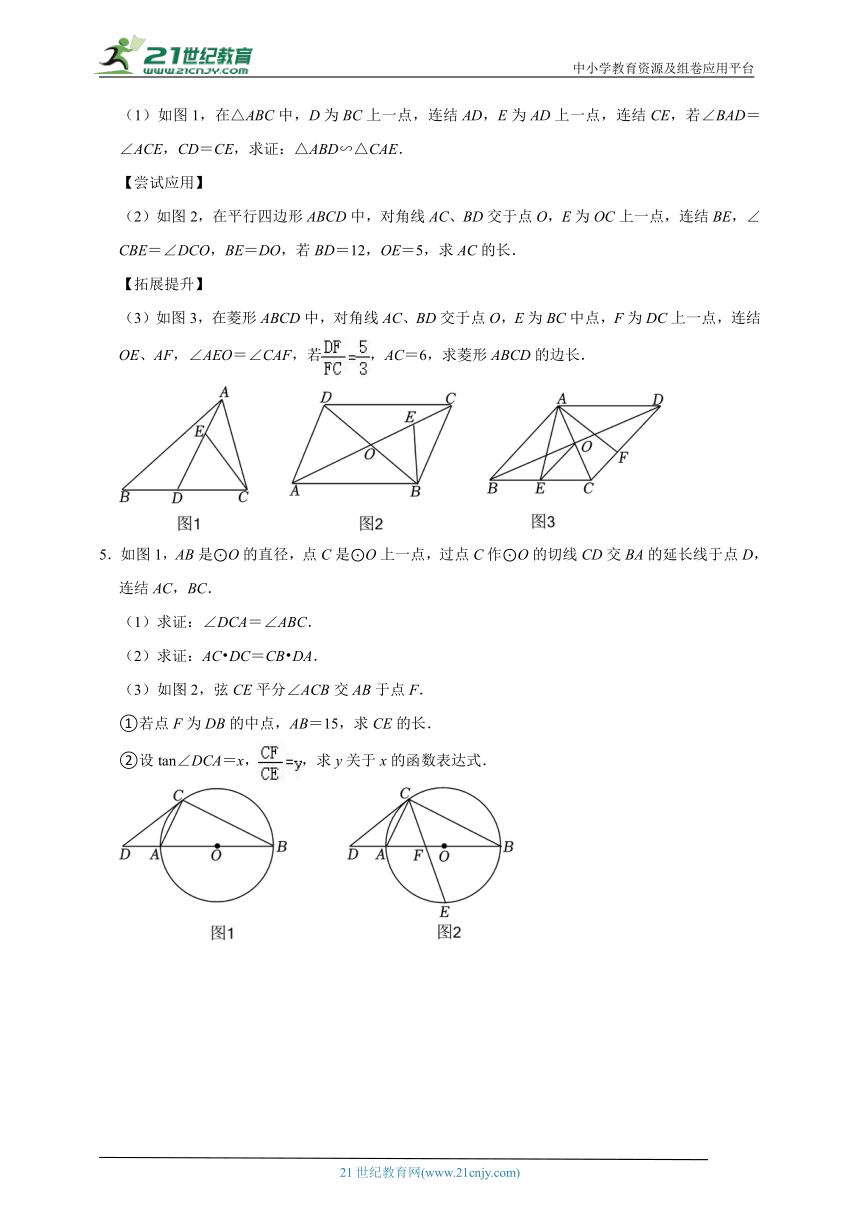
1.如图,将图1中的长方形纸片剪成①号、②号、③号、④号正方形和⑤号长方形,并将它们按图2的方式无重叠地放入另一个大长方形中,若需求出没有覆盖的阴影部分的周长,则下列说法中错误的是( )
A.只需知道图1中大长方形的周长即可
B.只需知道图2中大长方形的周长即可
C.只需知道③号正方形的周长即可
D.只需知道⑤号长方形的周长即可
2.如图,已知A为反比例函数y=(k>0)图象上一点,B为x轴正半轴上一点,过点B作BC⊥x轴交反比例函数图象于点C,连结OA,AB,OC.当OA=AB,△DBC的面积等于1时,k的值为 .
3.如图,在平面直角坐标系中,Rt△AOB斜边上的中点C在y轴正半轴上,M为AC的中点.反比例函数的图象经过点A,M,延长MO交函数在第四象限的图象于点N.反比例函数的图象经过点B,连结BN.若△BMN的面积为18,则m﹣n的值为 .
4.【基础巩固】
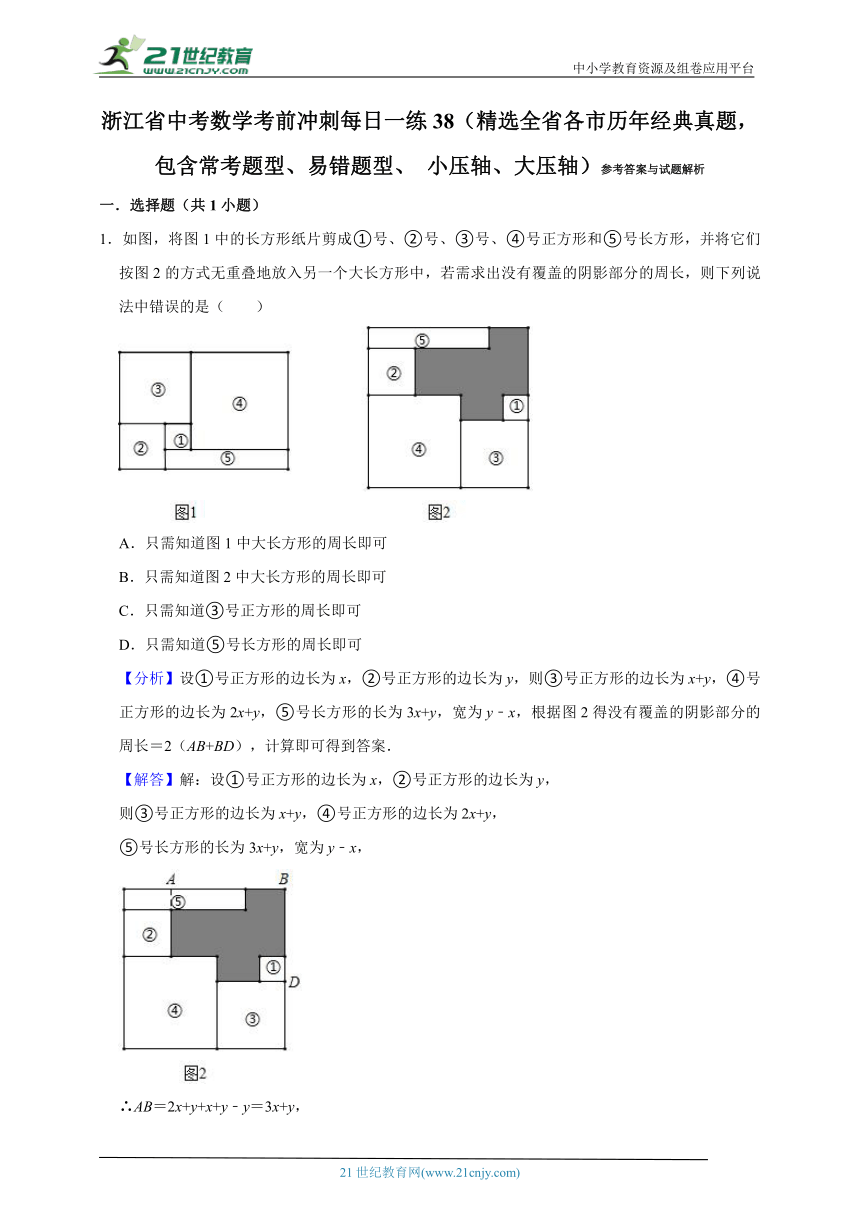
(1)如图1,在△ABC中,D为BC上一点,连结AD,E为AD上一点,连结CE,若∠BAD=∠ACE,CD=CE,求证:△ABD∽△CAE.
【尝试应用】
(2)如图2,在平行四边形ABCD中,对角线AC、BD交于点O,E为OC上一点,连结BE,∠CBE=∠DCO,BE=DO,若BD=12,OE=5,求AC的长.
【拓展提升】
(3)如图3,在菱形ABCD中,对角线AC、BD交于点O,E为BC中点,F为DC上一点,连结OE、AF,∠AEO=∠CAF,若,AC=6,求菱形ABCD的边长.
5.如图1,AB是⊙O的直径,点C是⊙O上一点,过点C作⊙O的切线CD交BA的延长线于点D,连结AC,BC.
(1)求证:∠DCA=∠ABC.
(2)求证:AC DC=CB DA.
(3)如图2,弦CE平分∠ACB交AB于点F.
①若点F为DB的中点,AB=15,求CE的长.
②设tan∠DCA=x,,求y关于x的函数表达式.
浙江省中考数学考前冲刺每日一练38(精选全省各市历年经典真题,包含常考题型、易错题型、 小压轴、大压轴)参考答案与试题解析
一.选择题(共1小题)
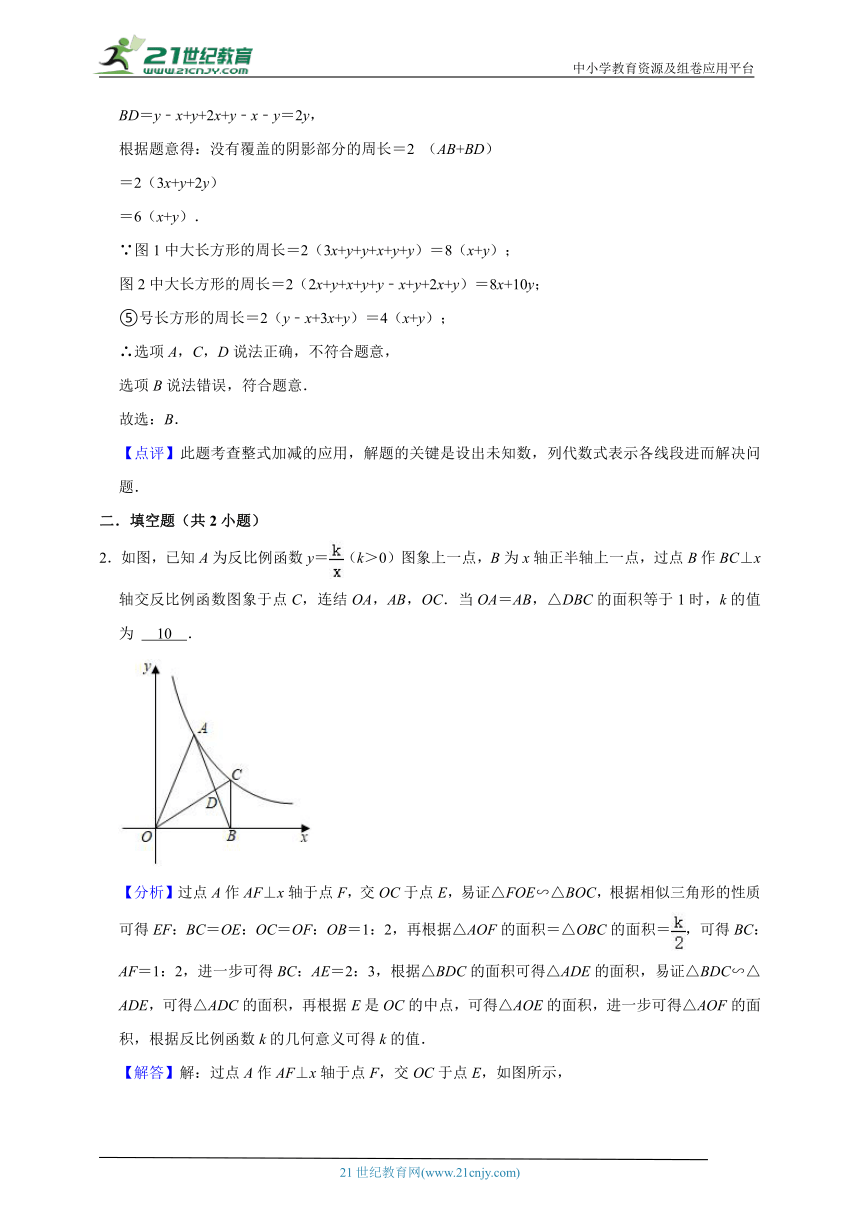
1.如图,将图1中的长方形纸片剪成①号、②号、③号、④号正方形和⑤号长方形,并将它们按图2的方式无重叠地放入另一个大长方形中,若需求出没有覆盖的阴影部分的周长,则下列说法中错误的是( )
A.只需知道图1中大长方形的周长即可
B.只需知道图2中大长方形的周长即可
C.只需知道③号正方形的周长即可
D.只需知道⑤号长方形的周长即可
【分析】设①号正方形的边长为x,②号正方形的边长为y,则③号正方形的边长为x+y,④号正方形的边长为2x+y,⑤号长方形的长为3x+y,宽为y﹣x,根据图2得没有覆盖的阴影部分的周长=2(AB+BD),计算即可得到答案.
【解答】解:设①号正方形的边长为x,②号正方形的边长为y,
则③号正方形的边长为x+y,④号正方形的边长为2x+y,
⑤号长方形的长为3x+y,宽为y﹣x,
∴AB=2x+y+x+y﹣y=3x+y,
BD=y﹣x+y+2x+y﹣x﹣y=2y,
根据题意得:没有覆盖的阴影部分的周长=2 (AB+BD)
=2(3x+y+2y)
=6(x+y).
∵图1中大长方形的周长=2(3x+y+y+x+y+y)=8(x+y);
图2中大长方形的周长=2(2x+y+x+y+y﹣x+y+2x+y)=8x+10y;
⑤号长方形的周长=2(y﹣x+3x+y)=4(x+y);
∴选项A,C,D说法正确,不符合题意,
选项B说法错误,符合题意.
故选:B.
【点评】此题考查整式加减的应用,解题的关键是设出未知数,列代数式表示各线段进而解决问题.
二.填空题(共2小题)
2.如图,已知A为反比例函数y=(k>0)图象上一点,B为x轴正半轴上一点,过点B作BC⊥x轴交反比例函数图象于点C,连结OA,AB,OC.当OA=AB,△DBC的面积等于1时,k的值为 10 .
【分析】过点A作AF⊥x轴于点F,交OC于点E,易证△FOE∽△BOC,根据相似三角形的性质可得EF:BC=OE:OC=OF:OB=1:2,再根据△AOF的面积=△OBC的面积=,可得BC:AF=1:2,进一步可得BC:AE=2:3,根据△BDC的面积可得△ADE的面积,易证△BDC∽△ADE,可得△ADC的面积,再根据E是OC的中点,可得△AOE的面积,进一步可得△AOF的面积,根据反比例函数k的几何意义可得k的值.
【解答】解:过点A作AF⊥x轴于点F,交OC于点E,如图所示,
∵AO=AB
∴OF=FB,
∵BC⊥x轴,
∴∠OBC=∠OFE=90°,
∵∠FOE=∠BOC,
∴△FOE∽△BOC,
∴EF:BC=OE:OC=OF:OB=1:2,
∵△AOF的面积=△OBC的面积=,
∵OF:OB=1:2,
∴AF:BC=2:1,
∵EF:BC=1:2,
∴BC:AE=2:3,
∵AF∥BC,
∴∠AED=∠BCD,∠EAD=∠CBD,
∴△BDC∽△ADE,
∵△DBC的面积等于1,
∴△ADE的面积为,
∵DC:DE=BC:AE=2:3,
∴△ADC的面积==,
∴△AEC的面积为=,
∴△AOE的面积为,
∵EF:AE=1:3,
∴△AEF的面积为=,
∴△AOF的面积为=5,
∴k=2×5=10,
故答案为:10.
【点评】本题考查了反比例函数k的几何意义,涉及相似三角形的判定和性质,三角形的面积等,熟练掌握反比例函数k的几何意义是解题的关键.
3.如图,在平面直角坐标系中,Rt△AOB斜边上的中点C在y轴正半轴上,M为AC的中点.反比例函数的图象经过点A,M,延长MO交函数在第四象限的图象于点N.反比例函数的图象经过点B,连结BN.若△BMN的面积为18,则m﹣n的值为 ﹣24 .
【分析】根据三角形中线平分三角形面积,求出三角形AOC和三角形BOC的面积都是6,在证明△ACD和△BCE全等,利用反比例函数的几何意义,表示出△AOD和△BOE的面积,再利用面积差求出m﹣n即可.
【解答】解:作BE⊥y轴于E,AD⊥x轴于D,
∵M,N关于O对称,则MO=NO,
∵△BMN的面积为18,
∴S△BMO=9,
∵点M为AC的中点,
∴MC=AC=BC,
∴S△BOM=3S△COM,
∴S△MOC=3,
∴S△AOC=S△BOC=6,
∵C是AB的中点,
∴AC=BC,
∵∠ADC=∠BEC=90°,∠BCE=∠ACG,
∴△ACD≌△BCE(AAS),
∴S△ACD=S△BCE,
即S△AOC﹣S△AOD=S△BOE﹣S△BOC,
∵S△AOD=,S△BOE=,
∴,
∴m﹣n=﹣24,
故答案为:﹣24.
【点评】本题考查了反比例函数的几何意义的应用,三角形中线平分面积的应用、三角形的全等的应用是解题关键.
三.解答题(共2小题)
4.【基础巩固】
(1)如图1,在△ABC中,D为BC上一点,连结AD,E为AD上一点,连结CE,若∠BAD=∠ACE,CD=CE,求证:△ABD∽△CAE.
【尝试应用】
(2)如图2,在平行四边形ABCD中,对角线AC、BD交于点O,E为OC上一点,连结BE,∠CBE=∠DCO,BE=DO,若BD=12,OE=5,求AC的长.
【拓展提升】
(3)如图3,在菱形ABCD中,对角线AC、BD交于点O,E为BC中点,F为DC上一点,连结OE、AF,∠AEO=∠CAF,若,AC=6,求菱形ABCD的边长.
【分析】(1)可证得∠CDE=∠CED,从而∠ADB=∠CEA,进一步得出结论;
(2)可证得∠BEO=∠BOE,从而得出∠BEC=∠COD,进而得出△BEC∽△COD,从而,设OC=x,则CE=OC﹣OE=x﹣5,从而得出,从而求得x的值,进一步得出结果;
(3)延长AG,BC,交于点G,可得出△CGF∽△DAF,从而,进而表示出CG,可证得△AOE∽△GCA,从而,进而求得t的值,进一步得出结果.
【解答】(1)证明:∵CD=CE,
∴∠CDE=∠CED,
∴180°﹣∠CDE=180°﹣∠CED,
∴∠ADB=∠CEA,
∵∠BAD=∠ACE,
∴△ABD∽△CAE.
(2)解:∵四边形ABCD是平行四边形,
∴,
∴BE=DO=BO=6.
∴∠BEO=∠BOE,
∴180°﹣∠BEO=180°﹣∠BOE,
∴∠BEC=∠COD.
∵∠CBE=∠DCO,
∴△BEC∽△COD,
∴,
设OC=x,则CE=OC﹣OE=x﹣5,
∴,
∴x1=9,x2=﹣4(舍去),
∴OC=9,
∴AC=2OC=18;
(3)解:如图,
延长AG,BC,交于点G.
∵,
∴设DF=5t,FC=3t,则CD=8t,
∵四边形ABCD是菱形,
∴AB=AD=BC=CD=8t,AD∥BC,,AC⊥BD,
∴△CGF∽△DAF,
∴,
即,
∴.
在Rt△BOC中,
∵E为BC的中点,
∴OE=CE=BC=4t.
∴∠COE=∠ACE,
∴∠AOE=∠ACG,
∵∠AEO=∠CAF,
∴△AOE∽△GCA,
∴,
即,
∴t1=,t2=﹣(舍去),
∴,
即菱形ABCD的边长为.
【点评】本题考查了平行四边形、菱形的性质,直角三角形和等腰三角形的性质,相似三角形的判定和性质等知识,解决问题的关键是作辅助线,构造相似三角形.
5.如图1,AB是⊙O的直径,点C是⊙O上一点,过点C作⊙O的切线CD交BA的延长线于点D,连结AC,BC.
(1)求证:∠DCA=∠ABC.
(2)求证:AC DC=CB DA.
(3)如图2,弦CE平分∠ACB交AB于点F.
①若点F为DB的中点,AB=15,求CE的长.
②设tan∠DCA=x,,求y关于x的函数表达式.
【分析】(1)根据切线的性质及圆周角定理推出∠DCA=∠BCO,根据等腰三角形的性质得出∠ABC=∠BCO,等量代换即可得解;
(2)根据相似三角形的判定与性质求解即可;
(3)①连结OE,BE,根据角平分线定义及圆周角定理推出,结合(2),根据相似三角形的性质推出DF=DC=10,AF=5,根据勾股定理推出AB=15,,,根据圆周角定理推出△OBE是等腰直角三角形,则,根据题意推出△ACF∽△ECB,根据相似三角形的性质即可得解;
②由(1)得,设CB=t,则AC=xt,根据勾股定理推出,根据相似三角形的判定与性质求解即可.
【解答】(1)证明:连结OC.
∵DC是⊙O的切线,
∴∠DCO=90°,
即∠DCA+∠ACO=∠DCO=90°,
∵AB是⊙O的直径,
∴∠ACB=90°,
即∠BCO+∠ACO=∠ACB=90°,
∴∠DCA=∠BCO,
∵OC=OB,
∴∠ABC=∠BCO,
∴∠DCA=∠ABC;
(2)证明:由(1)得∠DCA=∠ABC,
∵∠D=∠D,
∴△ACD∽△CBD,
∴,
∴AC DC=CB DA.
(3)解:①连结OE,BE.
∵弦CE平分∠ACB,∠ACB=90°,
∴,
∵∠DCA=∠ABC,
∴∠DCA+∠ACF=∠FCB+∠ABC,
即∠DCF=∠DFC,
∴DC=DF,
∵点F为DB的中点,
∴,
由(2)得△ACD∽△CBD,
∴==,
即,
∴,
∴,
∴DF=DC=10,
∴AF=5,
∵,
∵AC2+BC2=AB2,
∴,
∵AB=15,
∴,,
∵∠ECB=45°,
∴∠EOB=2∠ECB=90°,
∵OE=OB=,
∴△OEB是等腰直角三角形,
∴,
∵∠ACF=∠ECB,∠CAF=∠CEB,
∴△ACF∽△ECB,
∴,
∴CE==;
②∵∠ACB=90°,∠ABC=∠DCA,
∴,
设CB=t,则AC=xt,
∴AB2=AC2+CB2=(xt)2+t2=(x2+1)t2,
∴,
∵∠BEF=∠CEB,∠EBF=∠ACF=∠BCE,
∴△EBF∽△ECB,
∴,
∴EB2=EC EF,
∵△ACF∽△ECB,
∴,
∴AC CB=EC CF,
∴,
∴,
∴y=.
【点评】此题是圆的综合题,考查了切线的性质、圆周角定理、相似三角形的判定与性质、勾股定理、锐角三角函数等知识,熟练掌握切线的性质、圆周角定理、相似三角形的判定与性质、勾股定理、锐角三角函数等知识并作出合理的辅助线是解题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
浙江省中考数学考前冲刺每日一练38(精选全省各市历年经典真题,包含常考题型、易错题型、 小压轴、大压轴)
1.如图,将图1中的长方形纸片剪成①号、②号、③号、④号正方形和⑤号长方形,并将它们按图2的方式无重叠地放入另一个大长方形中,若需求出没有覆盖的阴影部分的周长,则下列说法中错误的是( )
A.只需知道图1中大长方形的周长即可
B.只需知道图2中大长方形的周长即可
C.只需知道③号正方形的周长即可
D.只需知道⑤号长方形的周长即可
2.如图,已知A为反比例函数y=(k>0)图象上一点,B为x轴正半轴上一点,过点B作BC⊥x轴交反比例函数图象于点C,连结OA,AB,OC.当OA=AB,△DBC的面积等于1时,k的值为 .
3.如图,在平面直角坐标系中,Rt△AOB斜边上的中点C在y轴正半轴上,M为AC的中点.反比例函数的图象经过点A,M,延长MO交函数在第四象限的图象于点N.反比例函数的图象经过点B,连结BN.若△BMN的面积为18,则m﹣n的值为 .
4.【基础巩固】
(1)如图1,在△ABC中,D为BC上一点,连结AD,E为AD上一点,连结CE,若∠BAD=∠ACE,CD=CE,求证:△ABD∽△CAE.
【尝试应用】
(2)如图2,在平行四边形ABCD中,对角线AC、BD交于点O,E为OC上一点,连结BE,∠CBE=∠DCO,BE=DO,若BD=12,OE=5,求AC的长.
【拓展提升】
(3)如图3,在菱形ABCD中,对角线AC、BD交于点O,E为BC中点,F为DC上一点,连结OE、AF,∠AEO=∠CAF,若,AC=6,求菱形ABCD的边长.
5.如图1,AB是⊙O的直径,点C是⊙O上一点,过点C作⊙O的切线CD交BA的延长线于点D,连结AC,BC.
(1)求证:∠DCA=∠ABC.
(2)求证:AC DC=CB DA.
(3)如图2,弦CE平分∠ACB交AB于点F.
①若点F为DB的中点,AB=15,求CE的长.
②设tan∠DCA=x,,求y关于x的函数表达式.
浙江省中考数学考前冲刺每日一练38(精选全省各市历年经典真题,包含常考题型、易错题型、 小压轴、大压轴)参考答案与试题解析
一.选择题(共1小题)
1.如图,将图1中的长方形纸片剪成①号、②号、③号、④号正方形和⑤号长方形,并将它们按图2的方式无重叠地放入另一个大长方形中,若需求出没有覆盖的阴影部分的周长,则下列说法中错误的是( )
A.只需知道图1中大长方形的周长即可
B.只需知道图2中大长方形的周长即可
C.只需知道③号正方形的周长即可
D.只需知道⑤号长方形的周长即可
【分析】设①号正方形的边长为x,②号正方形的边长为y,则③号正方形的边长为x+y,④号正方形的边长为2x+y,⑤号长方形的长为3x+y,宽为y﹣x,根据图2得没有覆盖的阴影部分的周长=2(AB+BD),计算即可得到答案.
【解答】解:设①号正方形的边长为x,②号正方形的边长为y,
则③号正方形的边长为x+y,④号正方形的边长为2x+y,
⑤号长方形的长为3x+y,宽为y﹣x,
∴AB=2x+y+x+y﹣y=3x+y,
BD=y﹣x+y+2x+y﹣x﹣y=2y,
根据题意得:没有覆盖的阴影部分的周长=2 (AB+BD)
=2(3x+y+2y)
=6(x+y).
∵图1中大长方形的周长=2(3x+y+y+x+y+y)=8(x+y);
图2中大长方形的周长=2(2x+y+x+y+y﹣x+y+2x+y)=8x+10y;
⑤号长方形的周长=2(y﹣x+3x+y)=4(x+y);
∴选项A,C,D说法正确,不符合题意,
选项B说法错误,符合题意.
故选:B.
【点评】此题考查整式加减的应用,解题的关键是设出未知数,列代数式表示各线段进而解决问题.
二.填空题(共2小题)
2.如图,已知A为反比例函数y=(k>0)图象上一点,B为x轴正半轴上一点,过点B作BC⊥x轴交反比例函数图象于点C,连结OA,AB,OC.当OA=AB,△DBC的面积等于1时,k的值为 10 .
【分析】过点A作AF⊥x轴于点F,交OC于点E,易证△FOE∽△BOC,根据相似三角形的性质可得EF:BC=OE:OC=OF:OB=1:2,再根据△AOF的面积=△OBC的面积=,可得BC:AF=1:2,进一步可得BC:AE=2:3,根据△BDC的面积可得△ADE的面积,易证△BDC∽△ADE,可得△ADC的面积,再根据E是OC的中点,可得△AOE的面积,进一步可得△AOF的面积,根据反比例函数k的几何意义可得k的值.
【解答】解:过点A作AF⊥x轴于点F,交OC于点E,如图所示,
∵AO=AB
∴OF=FB,
∵BC⊥x轴,
∴∠OBC=∠OFE=90°,
∵∠FOE=∠BOC,
∴△FOE∽△BOC,
∴EF:BC=OE:OC=OF:OB=1:2,
∵△AOF的面积=△OBC的面积=,
∵OF:OB=1:2,
∴AF:BC=2:1,
∵EF:BC=1:2,
∴BC:AE=2:3,
∵AF∥BC,
∴∠AED=∠BCD,∠EAD=∠CBD,
∴△BDC∽△ADE,
∵△DBC的面积等于1,
∴△ADE的面积为,
∵DC:DE=BC:AE=2:3,
∴△ADC的面积==,
∴△AEC的面积为=,
∴△AOE的面积为,
∵EF:AE=1:3,
∴△AEF的面积为=,
∴△AOF的面积为=5,
∴k=2×5=10,
故答案为:10.
【点评】本题考查了反比例函数k的几何意义,涉及相似三角形的判定和性质,三角形的面积等,熟练掌握反比例函数k的几何意义是解题的关键.
3.如图,在平面直角坐标系中,Rt△AOB斜边上的中点C在y轴正半轴上,M为AC的中点.反比例函数的图象经过点A,M,延长MO交函数在第四象限的图象于点N.反比例函数的图象经过点B,连结BN.若△BMN的面积为18,则m﹣n的值为 ﹣24 .
【分析】根据三角形中线平分三角形面积,求出三角形AOC和三角形BOC的面积都是6,在证明△ACD和△BCE全等,利用反比例函数的几何意义,表示出△AOD和△BOE的面积,再利用面积差求出m﹣n即可.
【解答】解:作BE⊥y轴于E,AD⊥x轴于D,
∵M,N关于O对称,则MO=NO,
∵△BMN的面积为18,
∴S△BMO=9,
∵点M为AC的中点,
∴MC=AC=BC,
∴S△BOM=3S△COM,
∴S△MOC=3,
∴S△AOC=S△BOC=6,
∵C是AB的中点,
∴AC=BC,
∵∠ADC=∠BEC=90°,∠BCE=∠ACG,
∴△ACD≌△BCE(AAS),
∴S△ACD=S△BCE,
即S△AOC﹣S△AOD=S△BOE﹣S△BOC,
∵S△AOD=,S△BOE=,
∴,
∴m﹣n=﹣24,
故答案为:﹣24.
【点评】本题考查了反比例函数的几何意义的应用,三角形中线平分面积的应用、三角形的全等的应用是解题关键.
三.解答题(共2小题)
4.【基础巩固】
(1)如图1,在△ABC中,D为BC上一点,连结AD,E为AD上一点,连结CE,若∠BAD=∠ACE,CD=CE,求证:△ABD∽△CAE.
【尝试应用】
(2)如图2,在平行四边形ABCD中,对角线AC、BD交于点O,E为OC上一点,连结BE,∠CBE=∠DCO,BE=DO,若BD=12,OE=5,求AC的长.
【拓展提升】
(3)如图3,在菱形ABCD中,对角线AC、BD交于点O,E为BC中点,F为DC上一点,连结OE、AF,∠AEO=∠CAF,若,AC=6,求菱形ABCD的边长.
【分析】(1)可证得∠CDE=∠CED,从而∠ADB=∠CEA,进一步得出结论;
(2)可证得∠BEO=∠BOE,从而得出∠BEC=∠COD,进而得出△BEC∽△COD,从而,设OC=x,则CE=OC﹣OE=x﹣5,从而得出,从而求得x的值,进一步得出结果;
(3)延长AG,BC,交于点G,可得出△CGF∽△DAF,从而,进而表示出CG,可证得△AOE∽△GCA,从而,进而求得t的值,进一步得出结果.
【解答】(1)证明:∵CD=CE,
∴∠CDE=∠CED,
∴180°﹣∠CDE=180°﹣∠CED,
∴∠ADB=∠CEA,
∵∠BAD=∠ACE,
∴△ABD∽△CAE.
(2)解:∵四边形ABCD是平行四边形,
∴,
∴BE=DO=BO=6.
∴∠BEO=∠BOE,
∴180°﹣∠BEO=180°﹣∠BOE,
∴∠BEC=∠COD.
∵∠CBE=∠DCO,
∴△BEC∽△COD,
∴,
设OC=x,则CE=OC﹣OE=x﹣5,
∴,
∴x1=9,x2=﹣4(舍去),
∴OC=9,
∴AC=2OC=18;
(3)解:如图,
延长AG,BC,交于点G.
∵,
∴设DF=5t,FC=3t,则CD=8t,
∵四边形ABCD是菱形,
∴AB=AD=BC=CD=8t,AD∥BC,,AC⊥BD,
∴△CGF∽△DAF,
∴,
即,
∴.
在Rt△BOC中,
∵E为BC的中点,
∴OE=CE=BC=4t.
∴∠COE=∠ACE,
∴∠AOE=∠ACG,
∵∠AEO=∠CAF,
∴△AOE∽△GCA,
∴,
即,
∴t1=,t2=﹣(舍去),
∴,
即菱形ABCD的边长为.
【点评】本题考查了平行四边形、菱形的性质,直角三角形和等腰三角形的性质,相似三角形的判定和性质等知识,解决问题的关键是作辅助线,构造相似三角形.
5.如图1,AB是⊙O的直径,点C是⊙O上一点,过点C作⊙O的切线CD交BA的延长线于点D,连结AC,BC.
(1)求证:∠DCA=∠ABC.
(2)求证:AC DC=CB DA.
(3)如图2,弦CE平分∠ACB交AB于点F.
①若点F为DB的中点,AB=15,求CE的长.
②设tan∠DCA=x,,求y关于x的函数表达式.
【分析】(1)根据切线的性质及圆周角定理推出∠DCA=∠BCO,根据等腰三角形的性质得出∠ABC=∠BCO,等量代换即可得解;
(2)根据相似三角形的判定与性质求解即可;
(3)①连结OE,BE,根据角平分线定义及圆周角定理推出,结合(2),根据相似三角形的性质推出DF=DC=10,AF=5,根据勾股定理推出AB=15,,,根据圆周角定理推出△OBE是等腰直角三角形,则,根据题意推出△ACF∽△ECB,根据相似三角形的性质即可得解;
②由(1)得,设CB=t,则AC=xt,根据勾股定理推出,根据相似三角形的判定与性质求解即可.
【解答】(1)证明:连结OC.
∵DC是⊙O的切线,
∴∠DCO=90°,
即∠DCA+∠ACO=∠DCO=90°,
∵AB是⊙O的直径,
∴∠ACB=90°,
即∠BCO+∠ACO=∠ACB=90°,
∴∠DCA=∠BCO,
∵OC=OB,
∴∠ABC=∠BCO,
∴∠DCA=∠ABC;
(2)证明:由(1)得∠DCA=∠ABC,
∵∠D=∠D,
∴△ACD∽△CBD,
∴,
∴AC DC=CB DA.
(3)解:①连结OE,BE.
∵弦CE平分∠ACB,∠ACB=90°,
∴,
∵∠DCA=∠ABC,
∴∠DCA+∠ACF=∠FCB+∠ABC,
即∠DCF=∠DFC,
∴DC=DF,
∵点F为DB的中点,
∴,
由(2)得△ACD∽△CBD,
∴==,
即,
∴,
∴,
∴DF=DC=10,
∴AF=5,
∵,
∵AC2+BC2=AB2,
∴,
∵AB=15,
∴,,
∵∠ECB=45°,
∴∠EOB=2∠ECB=90°,
∵OE=OB=,
∴△OEB是等腰直角三角形,
∴,
∵∠ACF=∠ECB,∠CAF=∠CEB,
∴△ACF∽△ECB,
∴,
∴CE==;
②∵∠ACB=90°,∠ABC=∠DCA,
∴,
设CB=t,则AC=xt,
∴AB2=AC2+CB2=(xt)2+t2=(x2+1)t2,
∴,
∵∠BEF=∠CEB,∠EBF=∠ACF=∠BCE,
∴△EBF∽△ECB,
∴,
∴EB2=EC EF,
∵△ACF∽△ECB,
∴,
∴AC CB=EC CF,
∴,
∴,
∴y=.
【点评】此题是圆的综合题,考查了切线的性质、圆周角定理、相似三角形的判定与性质、勾股定理、锐角三角函数等知识,熟练掌握切线的性质、圆周角定理、相似三角形的判定与性质、勾股定理、锐角三角函数等知识并作出合理的辅助线是解题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
