浙江省中考数学考前冲刺每日一练5(精选全省各市历年经典真题,包含常考题型、易错题型、 小压轴、大压轴)
文档属性
| 名称 | 浙江省中考数学考前冲刺每日一练5(精选全省各市历年经典真题,包含常考题型、易错题型、 小压轴、大压轴) | 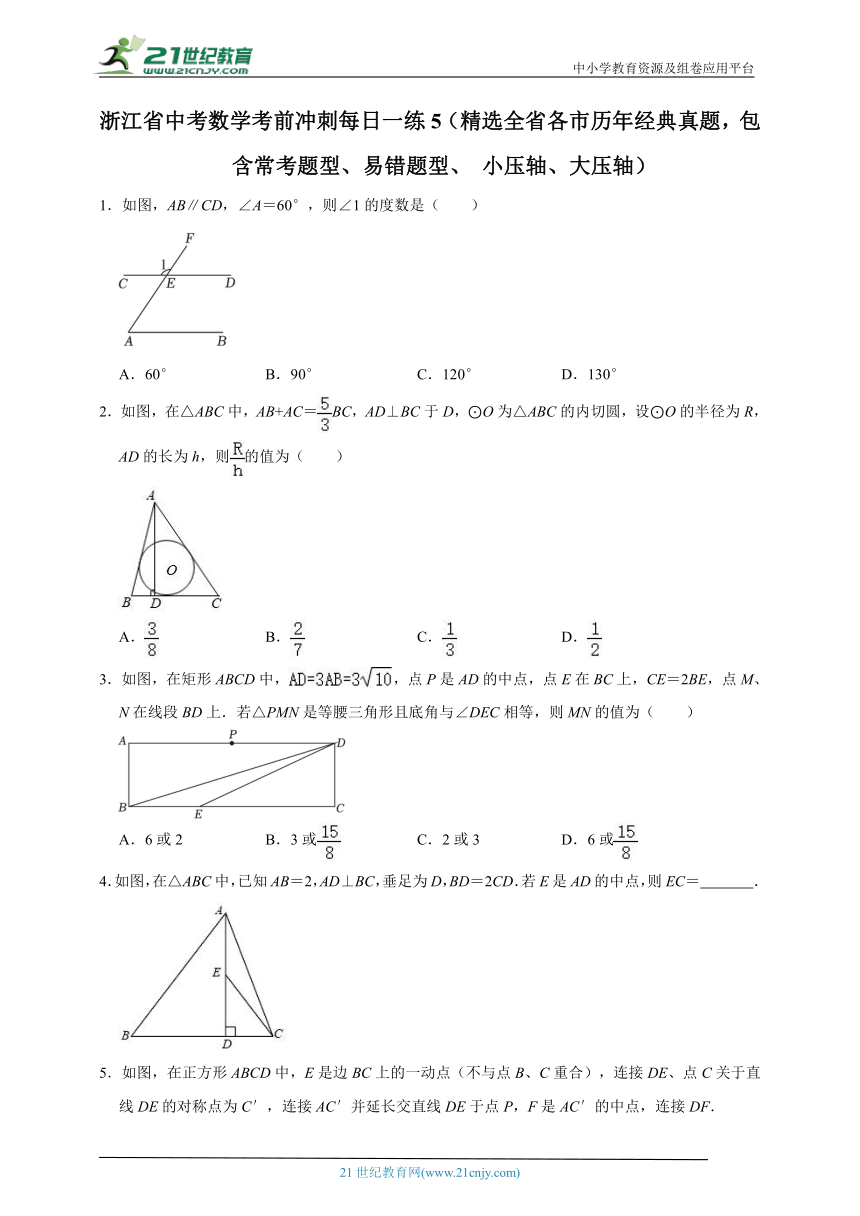 | |
| 格式 | doc | ||
| 文件大小 | 446.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-24 09:27:45 | ||
图片预览

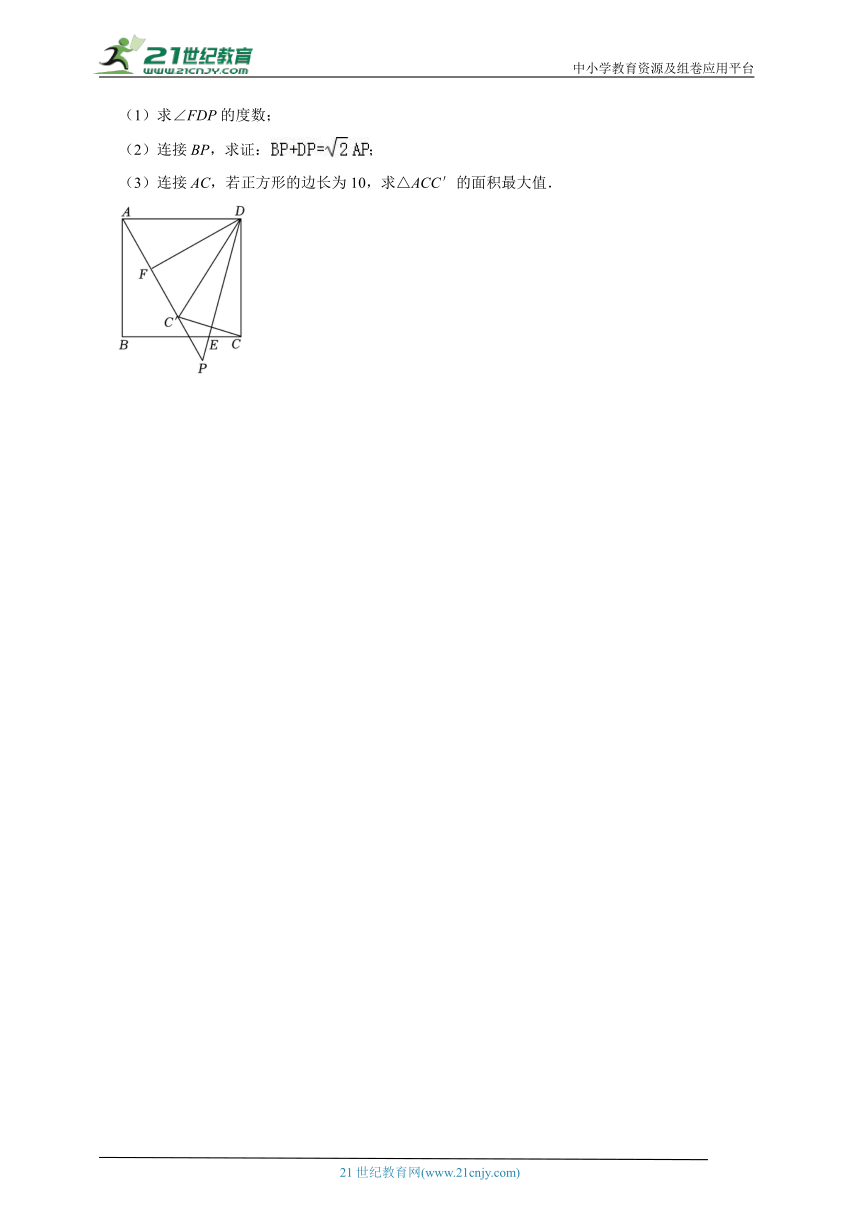



文档简介
中小学教育资源及组卷应用平台
浙江省中考数学考前冲刺每日一练5(精选全省各市历年经典真题,包含常考题型、易错题型、 小压轴、大压轴)
1.如图,AB∥CD,∠A=60°,则∠1的度数是( )
A.60° B.90° C.120° D.130°
2.如图,在△ABC中,AB+AC=BC,AD⊥BC于D,⊙O为△ABC的内切圆,设⊙O的半径为R,AD的长为h,则的值为( )
A. B. C. D.
3.如图,在矩形ABCD中,,点P是AD的中点,点E在BC上,CE=2BE,点M、N在线段BD上.若△PMN是等腰三角形且底角与∠DEC相等,则MN的值为( )
A.6或2 B.3或 C.2或3 D.6或
4.如图,在△ABC中,已知AB=2,AD⊥BC,垂足为D,BD=2CD.若E是AD的中点,则EC= .
5.如图,在正方形ABCD中,E是边BC上的一动点(不与点B、C重合),连接DE、点C关于直线DE的对称点为C′,连接AC′并延长交直线DE于点P,F是AC′的中点,连接DF.
(1)求∠FDP的度数;
(2)连接BP,求证:;
(3)连接AC,若正方形的边长为10,求△ACC′的面积最大值.
浙江省中考数学考前冲刺每日一练5(精选全省各市历年经典真题,包含常考题型、易错题型、 小压轴、大压轴)参考答案与试题解析
一.选择题(共3小题)
1.如图,AB∥CD,∠A=60°,则∠1的度数是( )
A.60° B.90° C.120° D.130°
【分析】由平行线的性质得到∠A+∠2=180°,求出∠2=120°,由对顶角的性质得到∠1=∠2=120°.
【解答】解:∵AB∥CD,
∴∠A+∠2=180°,
∵∠A=60°,
∴∠2=120°,
∵∠1、∠2是对顶角,
∴∠1=∠2=120°.
故选:C.
【点评】本题考查平行线的性质,对顶角的性质,关键是由平行线的性质得到∠A+∠2=180°.
2.如图,在△ABC中,AB+AC=BC,AD⊥BC于D,⊙O为△ABC的内切圆,设⊙O的半径为R,AD的长为h,则的值为( )
A. B. C. D.
【分析】根据三角形内切圆特点作出圆心和三条半径,分别表示出△ABC的面积,利用面积相等即可解决问题.
【解答】解:如图所示:O为△ABC中∠ABC、∠ACB、∠BAC的角平分线交点,过点O分别作垂线相交于AB、AC、BC于点E、G、F,
S△ABC=S△AOB+S△BOC+S△AOC=×AB R+BC R+AC R=R(AB+AC+BC),
∵AB+AC=BC,
∴S△ABC=R(BC+BC)=R BC,
∵AD的长为h,
∴S△ABC=BC h,
∴R BC=BC h,
∴h=R,
∴==,
故选:A.
【点评】本题考查三角形内切圆的相关性质,本题掌握三角形内切圆的性质,根据已知条件利用三角形ABC面积相等推出关系式是解题关键.
3.如图,在矩形ABCD中,,点P是AD的中点,点E在BC上,CE=2BE,点M、N在线段BD上.若△PMN 是等腰三角形且底角与∠DEC相等,则MN的值为( )
A.6或2 B.3或 C.2或3 D.6或
【分析】分两种情况:①MN为等腰△PMN的底边时,作PF⊥MN于F,则∠PFM=∠PFN=90°,由矩形的性质得出AB=CD,BC=AD=3AB=3,∠A=∠C=90°,得出AB=CD=,BD=10,证明△PDF∽△BDA,得出利用相似三角形的性质求出PF=,证出CE=2CD,由等腰三角形的性质得出MF=NF,∠PNF=∠DEC,证出△PNF∽△DEC,利用相似三角形的性质求出NF=2PF=3,即可得出答案;②MN为等腰△PMN的腰时,作PF⊥BD于F,由①得:PF=,MF=3,设MN=PN=x,则FN=3﹣x,在Rt△PNF中,由勾股定理得出方程,解方程即可.
【解答】解:分两种情况:
①MN为等腰△PMN的底边时,作PF⊥MN于F,如图所示:
则∠PFM=∠PFN=90°,
∵四边形ABCD是矩形,
∴AB=CD,BC=AD=3AB=3,∠A=∠C=90°,
∴AB=CD=,BD==10,
∵点P是AD的中点,
∴PD=AD=,
∵∠PDF=∠BDA,
∴△PDF∽△BDA,
∴,即,
解得:PF=,
∵CE=2BE,
∴BC=AD=3BE,
∴BE=CD,
∴CE=2CD,
∵△PMN是等腰三角形且底角与∠DEC相等,PF⊥MN,
∴MF=NF,∠PNF=∠DEC,
∵∠PFN=∠C=90°,
∴△PNF∽△DEC,
∴,
∴MF=NF=2PF=3,
∴MN=2NF=6;
②MN为等腰△PMN的腰时,作PF⊥BD于F,如图所示:
由①得:PF=,MF=3,
设MN=PN=x,则FN=3﹣x,
在Rt△PNF中,()2+(3﹣x)2=x2,
解得:x=,即MN=;
综上所述,MN的长为6或.
故选:D.
【点评】本题考查了矩形的性质、等腰三角形的性质、相似三角形的判定与性质、勾股定理等知识;熟练掌握矩形的性质和等腰三角形的性质,证明三角形相似是解题的关键.
二.填空题(共1小题)
4.如图,在△ABC中,已知AB=2,AD⊥BC,垂足为D,BD=2CD.若E是AD的中点,则EC= 1 .
【分析】设AE=ED=x,CD=y,根据勾股定理即可求出答案.
【解答】解:设AE=ED=x,CD=y,
∴BD=2y,
∵AD⊥BC,
∴∠ADB=∠ADC=90°,
在Rt△ABD中,
∴AB2=4x2+4y2,
∴x2+y2=1,
在Rt△CDE中,
∴EC2=x2+y2=1
∵EC>0
∴EC=1.
另解1:依据AD⊥BC,BD=2CD,E是AD的中点,
即可得判定△CDE∽△BDA,
且相似比为1:2,
∴=,
即CE=1.
另解2:取AB中点F,连接DF、FE,
∴DF=AB=1,
∵E是AD中点,
∴FE=BD,FE∥BD,
∵BD=2DC,
∴FE∥DC,FE=DC,
∴四边形FECD是平行四边形,
∴EC=FD=1,
故答案为:1.
【点评】本题考查勾股定理、中位线、相似三角形的性质与判定,直角三角形斜边上的中线的性质,本题属于基础题型.
三.解答题(共1小题)
5.如图,在正方形ABCD中,E是边BC上的一动点(不与点B、C重合),连接DE、点C关于直线DE的对称点为C′,连接AC′并延长交直线DE于点P,F是AC′的中点,连接DF.
(1)求∠FDP的度数;
(2)连接BP,求证:;
(3)连接AC,若正方形的边长为10,求△ACC′的面积最大值.
【分析】(1)证明∠CDE=∠C'DE和∠ADF=∠C'DF,可得∠FDP'=∠ADC=45°;
(2)作辅助线,构建全等三角形,证明△BAP≌△DAP'(SAS),得BP=DP',从而得△PAP'是等腰直角三角形,可得结论;
(3)先作高线C'G,确定△ACC′的面积中底边AC为定值10,根据高的大小确定面积的大小,当C'在BD上时,C'G最大,其△ACC′的面积最大,并求此时的面积.
【解答】(1)解:由对称得:CD=C'D,∠CDE=∠C'DE,
在正方形ABCD中,AD=CD,∠ADC=90°,
∴AD=C'D,
∵F是AC'的中点,
∴DF⊥AC',∠ADF=∠C'DF,
∴∠FDP=∠FDC'+∠EDC'=∠ADC=45°;
(2)证明:如图,作AP'⊥AP交PD的延长线于P',
∴∠PAP'=90°,
在正方形ABCD中,DA=BA,∠BAD=90°=∠PAP′,
∴∠DAP'=∠BAP,
由(1)可知:∠FDP=45°,
∵∠DFP=90°,
∴∠APD=45°,
∴∠P'=45°,
∴AP=AP',
在△BAP和△DAP'中,
,
∴△BAP≌△DAP'(SAS),
∴BP=DP',
∴DP+BP=DP+DP′=PP',
在Rt△APP′中,AP=AP',
∴PP′=AP,
∴BP+DP=AP;
(3)解:如图,过C'作C'G⊥AC于G,则S△AC'C=AC C'G,
在Rt△ABC中,AB=BC=10,
∴AC==10,即AC为定值,
当C'G最大时,△AC'C的面积最大,
连接BD,交AC于O,当C'在BD上时,C'G最大,此时G与O重合,
∵CD=C'D=10,OD=AC=5,
∴C'G=10﹣5,
∴S△AC'C=AC C'G=×10×(10﹣5)=50﹣50,
即△ACC′的面积最大值为50﹣50.
【点评】本题考查四边形综合题、正方形的性质、等腰直角三角形的判定和性质、全等三角形的判定和性质等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
浙江省中考数学考前冲刺每日一练5(精选全省各市历年经典真题,包含常考题型、易错题型、 小压轴、大压轴)
1.如图,AB∥CD,∠A=60°,则∠1的度数是( )
A.60° B.90° C.120° D.130°
2.如图,在△ABC中,AB+AC=BC,AD⊥BC于D,⊙O为△ABC的内切圆,设⊙O的半径为R,AD的长为h,则的值为( )
A. B. C. D.
3.如图,在矩形ABCD中,,点P是AD的中点,点E在BC上,CE=2BE,点M、N在线段BD上.若△PMN是等腰三角形且底角与∠DEC相等,则MN的值为( )
A.6或2 B.3或 C.2或3 D.6或
4.如图,在△ABC中,已知AB=2,AD⊥BC,垂足为D,BD=2CD.若E是AD的中点,则EC= .
5.如图,在正方形ABCD中,E是边BC上的一动点(不与点B、C重合),连接DE、点C关于直线DE的对称点为C′,连接AC′并延长交直线DE于点P,F是AC′的中点,连接DF.
(1)求∠FDP的度数;
(2)连接BP,求证:;
(3)连接AC,若正方形的边长为10,求△ACC′的面积最大值.
浙江省中考数学考前冲刺每日一练5(精选全省各市历年经典真题,包含常考题型、易错题型、 小压轴、大压轴)参考答案与试题解析
一.选择题(共3小题)
1.如图,AB∥CD,∠A=60°,则∠1的度数是( )
A.60° B.90° C.120° D.130°
【分析】由平行线的性质得到∠A+∠2=180°,求出∠2=120°,由对顶角的性质得到∠1=∠2=120°.
【解答】解:∵AB∥CD,
∴∠A+∠2=180°,
∵∠A=60°,
∴∠2=120°,
∵∠1、∠2是对顶角,
∴∠1=∠2=120°.
故选:C.
【点评】本题考查平行线的性质,对顶角的性质,关键是由平行线的性质得到∠A+∠2=180°.
2.如图,在△ABC中,AB+AC=BC,AD⊥BC于D,⊙O为△ABC的内切圆,设⊙O的半径为R,AD的长为h,则的值为( )
A. B. C. D.
【分析】根据三角形内切圆特点作出圆心和三条半径,分别表示出△ABC的面积,利用面积相等即可解决问题.
【解答】解:如图所示:O为△ABC中∠ABC、∠ACB、∠BAC的角平分线交点,过点O分别作垂线相交于AB、AC、BC于点E、G、F,
S△ABC=S△AOB+S△BOC+S△AOC=×AB R+BC R+AC R=R(AB+AC+BC),
∵AB+AC=BC,
∴S△ABC=R(BC+BC)=R BC,
∵AD的长为h,
∴S△ABC=BC h,
∴R BC=BC h,
∴h=R,
∴==,
故选:A.
【点评】本题考查三角形内切圆的相关性质,本题掌握三角形内切圆的性质,根据已知条件利用三角形ABC面积相等推出关系式是解题关键.
3.如图,在矩形ABCD中,,点P是AD的中点,点E在BC上,CE=2BE,点M、N在线段BD上.若△PMN 是等腰三角形且底角与∠DEC相等,则MN的值为( )
A.6或2 B.3或 C.2或3 D.6或
【分析】分两种情况:①MN为等腰△PMN的底边时,作PF⊥MN于F,则∠PFM=∠PFN=90°,由矩形的性质得出AB=CD,BC=AD=3AB=3,∠A=∠C=90°,得出AB=CD=,BD=10,证明△PDF∽△BDA,得出利用相似三角形的性质求出PF=,证出CE=2CD,由等腰三角形的性质得出MF=NF,∠PNF=∠DEC,证出△PNF∽△DEC,利用相似三角形的性质求出NF=2PF=3,即可得出答案;②MN为等腰△PMN的腰时,作PF⊥BD于F,由①得:PF=,MF=3,设MN=PN=x,则FN=3﹣x,在Rt△PNF中,由勾股定理得出方程,解方程即可.
【解答】解:分两种情况:
①MN为等腰△PMN的底边时,作PF⊥MN于F,如图所示:
则∠PFM=∠PFN=90°,
∵四边形ABCD是矩形,
∴AB=CD,BC=AD=3AB=3,∠A=∠C=90°,
∴AB=CD=,BD==10,
∵点P是AD的中点,
∴PD=AD=,
∵∠PDF=∠BDA,
∴△PDF∽△BDA,
∴,即,
解得:PF=,
∵CE=2BE,
∴BC=AD=3BE,
∴BE=CD,
∴CE=2CD,
∵△PMN是等腰三角形且底角与∠DEC相等,PF⊥MN,
∴MF=NF,∠PNF=∠DEC,
∵∠PFN=∠C=90°,
∴△PNF∽△DEC,
∴,
∴MF=NF=2PF=3,
∴MN=2NF=6;
②MN为等腰△PMN的腰时,作PF⊥BD于F,如图所示:
由①得:PF=,MF=3,
设MN=PN=x,则FN=3﹣x,
在Rt△PNF中,()2+(3﹣x)2=x2,
解得:x=,即MN=;
综上所述,MN的长为6或.
故选:D.
【点评】本题考查了矩形的性质、等腰三角形的性质、相似三角形的判定与性质、勾股定理等知识;熟练掌握矩形的性质和等腰三角形的性质,证明三角形相似是解题的关键.
二.填空题(共1小题)
4.如图,在△ABC中,已知AB=2,AD⊥BC,垂足为D,BD=2CD.若E是AD的中点,则EC= 1 .
【分析】设AE=ED=x,CD=y,根据勾股定理即可求出答案.
【解答】解:设AE=ED=x,CD=y,
∴BD=2y,
∵AD⊥BC,
∴∠ADB=∠ADC=90°,
在Rt△ABD中,
∴AB2=4x2+4y2,
∴x2+y2=1,
在Rt△CDE中,
∴EC2=x2+y2=1
∵EC>0
∴EC=1.
另解1:依据AD⊥BC,BD=2CD,E是AD的中点,
即可得判定△CDE∽△BDA,
且相似比为1:2,
∴=,
即CE=1.
另解2:取AB中点F,连接DF、FE,
∴DF=AB=1,
∵E是AD中点,
∴FE=BD,FE∥BD,
∵BD=2DC,
∴FE∥DC,FE=DC,
∴四边形FECD是平行四边形,
∴EC=FD=1,
故答案为:1.
【点评】本题考查勾股定理、中位线、相似三角形的性质与判定,直角三角形斜边上的中线的性质,本题属于基础题型.
三.解答题(共1小题)
5.如图,在正方形ABCD中,E是边BC上的一动点(不与点B、C重合),连接DE、点C关于直线DE的对称点为C′,连接AC′并延长交直线DE于点P,F是AC′的中点,连接DF.
(1)求∠FDP的度数;
(2)连接BP,求证:;
(3)连接AC,若正方形的边长为10,求△ACC′的面积最大值.
【分析】(1)证明∠CDE=∠C'DE和∠ADF=∠C'DF,可得∠FDP'=∠ADC=45°;
(2)作辅助线,构建全等三角形,证明△BAP≌△DAP'(SAS),得BP=DP',从而得△PAP'是等腰直角三角形,可得结论;
(3)先作高线C'G,确定△ACC′的面积中底边AC为定值10,根据高的大小确定面积的大小,当C'在BD上时,C'G最大,其△ACC′的面积最大,并求此时的面积.
【解答】(1)解:由对称得:CD=C'D,∠CDE=∠C'DE,
在正方形ABCD中,AD=CD,∠ADC=90°,
∴AD=C'D,
∵F是AC'的中点,
∴DF⊥AC',∠ADF=∠C'DF,
∴∠FDP=∠FDC'+∠EDC'=∠ADC=45°;
(2)证明:如图,作AP'⊥AP交PD的延长线于P',
∴∠PAP'=90°,
在正方形ABCD中,DA=BA,∠BAD=90°=∠PAP′,
∴∠DAP'=∠BAP,
由(1)可知:∠FDP=45°,
∵∠DFP=90°,
∴∠APD=45°,
∴∠P'=45°,
∴AP=AP',
在△BAP和△DAP'中,
,
∴△BAP≌△DAP'(SAS),
∴BP=DP',
∴DP+BP=DP+DP′=PP',
在Rt△APP′中,AP=AP',
∴PP′=AP,
∴BP+DP=AP;
(3)解:如图,过C'作C'G⊥AC于G,则S△AC'C=AC C'G,
在Rt△ABC中,AB=BC=10,
∴AC==10,即AC为定值,
当C'G最大时,△AC'C的面积最大,
连接BD,交AC于O,当C'在BD上时,C'G最大,此时G与O重合,
∵CD=C'D=10,OD=AC=5,
∴C'G=10﹣5,
∴S△AC'C=AC C'G=×10×(10﹣5)=50﹣50,
即△ACC′的面积最大值为50﹣50.
【点评】本题考查四边形综合题、正方形的性质、等腰直角三角形的判定和性质、全等三角形的判定和性质等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
