浙江省中考数学考前冲刺每日一练6(精选全省各市历年经典真题,包含常考题型、易错题型、 小压轴、大压轴)
文档属性
| 名称 | 浙江省中考数学考前冲刺每日一练6(精选全省各市历年经典真题,包含常考题型、易错题型、 小压轴、大压轴) |

|
|
| 格式 | doc | ||
| 文件大小 | 367.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-24 00:00:00 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
浙江省中考数学考前冲刺每日一练6(精选全省各市历年经典真题,包含常考题型、易错题型、 小压轴、大压轴)
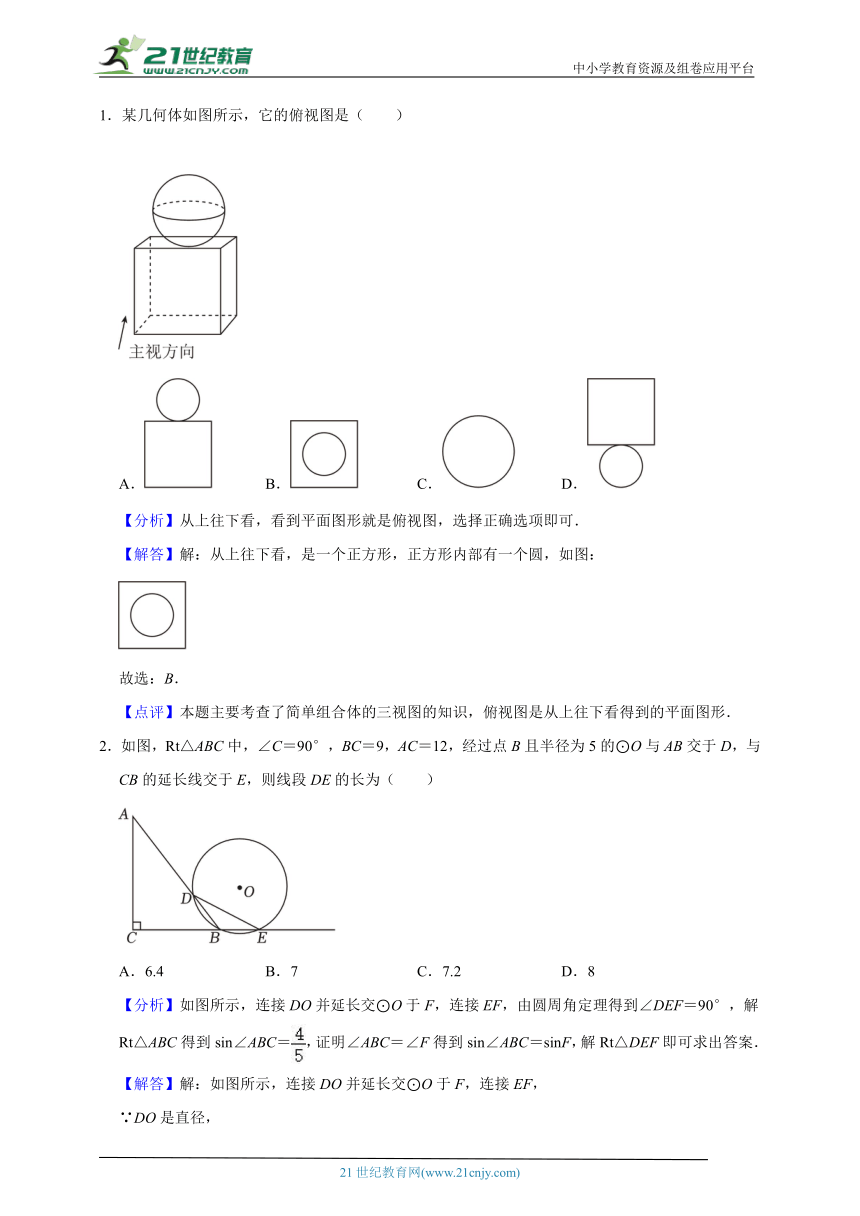
1.某几何体如图所示,它的俯视图是( )
A. B. C. D.
2.如图,Rt△ABC中,∠C=90°,BC=9,AC=12,经过点B且半径为5的⊙O与AB交于D,与CB的延长线交于E,则线段DE的长为( )
A.6.4 B.7 C.7.2 D.8
3.对于一个函数:当自变量x取a时,其函数值y也等于a,我们称a为这个函数的不动点.若二次函数y=x2+2x+c(c为常数)有两个不相等且都小于1的不动点,则c的取值范围是( )
A.c<﹣3 B.﹣3<c<﹣2 C.﹣2<c< D.c>
4.如图,直线y=﹣2x+4与x轴,y轴分别相交于点A、B,四边形ABCD是正方形,双曲线y=在第一象限经过点D,将正方形向下平移m个单位后,点C刚好落在双曲线上,则m= .
5.一组有序排列的数具有如下规律:任意相邻的三个数,中间的数等于前后两数的积.若这组数第1个数是a,第5个数是,则第2028个数是 (用含a的式子表示).
浙江省中考数学考前冲刺每日一练6(精选全省各市历年经典真题,包含常考题型、易错题型、 小压轴、大压轴)参考答案与试题解析
一.选择题(共3小题)
1.某几何体如图所示,它的俯视图是( )
A. B. C. D.
【分析】从上往下看,看到平面图形就是俯视图,选择正确选项即可.
【解答】解:从上往下看,是一个正方形,正方形内部有一个圆,如图:
故选:B.
【点评】本题主要考查了简单组合体的三视图的知识,俯视图是从上往下看得到的平面图形.
2.如图,Rt△ABC中,∠C=90°,BC=9,AC=12,经过点B且半径为5的⊙O与AB交于D,与CB的延长线交于E,则线段DE的长为( )
A.6.4 B.7 C.7.2 D.8
【分析】如图所示,连接DO并延长交⊙O于F,连接EF,由圆周角定理得到∠DEF=90°,解Rt△ABC得到sin∠ABC=,证明∠ABC=∠F得到sin∠ABC=sinF,解Rt△DEF即可求出答案.
【解答】解:如图所示,连接DO并延长交⊙O于F,连接EF,
∵DO是直径,
∴∠DEF=90°,
在Rt△ABC中,∠C=90°,BC=9,AC=12,
∴AB==15,
∴sin∠ABC==,
∵四边形BDFE是圆内接四边形,
∴∠F+∠DBE=180°,
又∵∠ABC+∠DBE=180°,
∴∠ABC=∠F,
∴sin∠ABC=sinF,
在Rt△DEF中,sinF==,
∴DE=DF=10×=8,
故选:D.
【点评】本题主要考查了解直角三角形,圆周角定理,圆内接四边形的性质,勾股定理等等,正确作出辅助线构造直角三角形是解题的关键.
3.对于一个函数:当自变量x取a时,其函数值y也等于a,我们称a为这个函数的不动点.若二次函数y=x2+2x+c(c为常数)有两个不相等且都小于1的不动点,则c的取值范围是( )
A.c<﹣3 B.﹣3<c<﹣2 C.﹣2<c< D.c>
【分析】由函数的不动点概念得出x1、x2是方程x2+2x+c=x的两个实数根,由Δ>0且x=1时y>0,即可求解.
【解答】解:由题意知二次函数y=x2+2x+c有两个相异的不动点x1、x2是方程x2+2x+c=x的两个不相等实数根,且x1、x2都小于1,
整理,得:x2+x+c=0,
由x2+x+c=0有两个不相等的实数根知:Δ>0,即1﹣4c>0①,
令y=x2+x+c,画出该二次函数的草图如下:
而x1、x2(设x2在x1的右侧)都小于1,即当x=1时,y=x2+x+c=2+c>0②,
联立①②并解得:﹣2<c<;
故选:C.
【点评】本题主要考查二次函数图象与系数的关系,解题的关键是理解并掌握不动点的概念,并据此得出关于c的不等式.
二.填空题(共2小题)
4.如图,直线y=﹣2x+4与x轴,y轴分别相交于点A、B,四边形ABCD是正方形,双曲线y=在第一象限经过点D,将正方形向下平移m个单位后,点C刚好落在双曲线上,则m= 3 .
【分析】过点D作DE⊥x轴于点E,作CF⊥x轴于点F,作DG⊥CF于G,证明△AOB≌△DEA,利用待定系数法求出反比例函数的解析式,证明△AOB≌△DGC,求出平移后点C的纵坐标,解答即可.
【解答】解:过点D作DE⊥x轴于点E,作CF⊥x轴于点F,作DG⊥CF于G,
∵直线y=﹣2x+4与x轴,y轴相交于点A.B,
∴当x=0时,y=4,即OB=4.
当y=0时,x=2,即OA=2.
∵四边形ABCD是正方形,
∴∠BAD=90°,AB=AD.
∴∠BAO+∠DAE=90°.
∵∠ADE+∠DAE=90°,
∴∠BAO=∠ADE,
在△AOB和△DEA中,
,
∴△AOB≌△DEA(AAS),
∴DE=AO=2,AE=BO=4,
∴OE=6,DE=2.
∴点D 的坐标为(6,2)
把(6,2)代入 y=,得k=12,
则反比例函数的解析式为:y=,
同理,△AOB≌△DGC,
∴CG=OB=4,DG=OA=2,
则OF=4,CF=6,
把x=4代入y=,得y=3,
∴m=6﹣3=3
∴将正方形向下平移3个单位后,点C刚好落在双曲线上,
故答案为:3.
【点评】本题考查的是反比例函数与一次函数的交点问题、坐标与图形变化﹣平移问题、正方形的性质,掌握待定系数法求函数解析式的一般步骤、平移的性质是解题的关键.
5.一组有序排列的数具有如下规律:任意相邻的三个数,中间的数等于前后两数的积.若这组数第1个数是a,第5个数是,则第2028个数是 (用含a的式子表示).
【分析】设第2个数为x,第3个数为y,第4个数为z,根据任意相邻的三个数,中间的数等于前后两数的积,求出x,y,z,进而得到这组数每6个一组进行循环,进一步求出第2028个数即可.
【解答】解:设第2个数为x,第3个数为y,第4个数为z,由题意,得:,
∴,
∴这组数据为,即:这组数以6个为一组,进行循环,
∵2028÷6=338,
∴第2028个数是;
故答案为:.
【点评】本题考查数字类规律探究,解题的关键是找到规律.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
浙江省中考数学考前冲刺每日一练6(精选全省各市历年经典真题,包含常考题型、易错题型、 小压轴、大压轴)
1.某几何体如图所示,它的俯视图是( )
A. B. C. D.
2.如图,Rt△ABC中,∠C=90°,BC=9,AC=12,经过点B且半径为5的⊙O与AB交于D,与CB的延长线交于E,则线段DE的长为( )
A.6.4 B.7 C.7.2 D.8
3.对于一个函数:当自变量x取a时,其函数值y也等于a,我们称a为这个函数的不动点.若二次函数y=x2+2x+c(c为常数)有两个不相等且都小于1的不动点,则c的取值范围是( )
A.c<﹣3 B.﹣3<c<﹣2 C.﹣2<c< D.c>
4.如图,直线y=﹣2x+4与x轴,y轴分别相交于点A、B,四边形ABCD是正方形,双曲线y=在第一象限经过点D,将正方形向下平移m个单位后,点C刚好落在双曲线上,则m= .
5.一组有序排列的数具有如下规律:任意相邻的三个数,中间的数等于前后两数的积.若这组数第1个数是a,第5个数是,则第2028个数是 (用含a的式子表示).
浙江省中考数学考前冲刺每日一练6(精选全省各市历年经典真题,包含常考题型、易错题型、 小压轴、大压轴)参考答案与试题解析
一.选择题(共3小题)
1.某几何体如图所示,它的俯视图是( )
A. B. C. D.
【分析】从上往下看,看到平面图形就是俯视图,选择正确选项即可.
【解答】解:从上往下看,是一个正方形,正方形内部有一个圆,如图:
故选:B.
【点评】本题主要考查了简单组合体的三视图的知识,俯视图是从上往下看得到的平面图形.
2.如图,Rt△ABC中,∠C=90°,BC=9,AC=12,经过点B且半径为5的⊙O与AB交于D,与CB的延长线交于E,则线段DE的长为( )
A.6.4 B.7 C.7.2 D.8
【分析】如图所示,连接DO并延长交⊙O于F,连接EF,由圆周角定理得到∠DEF=90°,解Rt△ABC得到sin∠ABC=,证明∠ABC=∠F得到sin∠ABC=sinF,解Rt△DEF即可求出答案.
【解答】解:如图所示,连接DO并延长交⊙O于F,连接EF,
∵DO是直径,
∴∠DEF=90°,
在Rt△ABC中,∠C=90°,BC=9,AC=12,
∴AB==15,
∴sin∠ABC==,
∵四边形BDFE是圆内接四边形,
∴∠F+∠DBE=180°,
又∵∠ABC+∠DBE=180°,
∴∠ABC=∠F,
∴sin∠ABC=sinF,
在Rt△DEF中,sinF==,
∴DE=DF=10×=8,
故选:D.
【点评】本题主要考查了解直角三角形,圆周角定理,圆内接四边形的性质,勾股定理等等,正确作出辅助线构造直角三角形是解题的关键.
3.对于一个函数:当自变量x取a时,其函数值y也等于a,我们称a为这个函数的不动点.若二次函数y=x2+2x+c(c为常数)有两个不相等且都小于1的不动点,则c的取值范围是( )
A.c<﹣3 B.﹣3<c<﹣2 C.﹣2<c< D.c>
【分析】由函数的不动点概念得出x1、x2是方程x2+2x+c=x的两个实数根,由Δ>0且x=1时y>0,即可求解.
【解答】解:由题意知二次函数y=x2+2x+c有两个相异的不动点x1、x2是方程x2+2x+c=x的两个不相等实数根,且x1、x2都小于1,
整理,得:x2+x+c=0,
由x2+x+c=0有两个不相等的实数根知:Δ>0,即1﹣4c>0①,
令y=x2+x+c,画出该二次函数的草图如下:
而x1、x2(设x2在x1的右侧)都小于1,即当x=1时,y=x2+x+c=2+c>0②,
联立①②并解得:﹣2<c<;
故选:C.
【点评】本题主要考查二次函数图象与系数的关系,解题的关键是理解并掌握不动点的概念,并据此得出关于c的不等式.
二.填空题(共2小题)
4.如图,直线y=﹣2x+4与x轴,y轴分别相交于点A、B,四边形ABCD是正方形,双曲线y=在第一象限经过点D,将正方形向下平移m个单位后,点C刚好落在双曲线上,则m= 3 .
【分析】过点D作DE⊥x轴于点E,作CF⊥x轴于点F,作DG⊥CF于G,证明△AOB≌△DEA,利用待定系数法求出反比例函数的解析式,证明△AOB≌△DGC,求出平移后点C的纵坐标,解答即可.
【解答】解:过点D作DE⊥x轴于点E,作CF⊥x轴于点F,作DG⊥CF于G,
∵直线y=﹣2x+4与x轴,y轴相交于点A.B,
∴当x=0时,y=4,即OB=4.
当y=0时,x=2,即OA=2.
∵四边形ABCD是正方形,
∴∠BAD=90°,AB=AD.
∴∠BAO+∠DAE=90°.
∵∠ADE+∠DAE=90°,
∴∠BAO=∠ADE,
在△AOB和△DEA中,
,
∴△AOB≌△DEA(AAS),
∴DE=AO=2,AE=BO=4,
∴OE=6,DE=2.
∴点D 的坐标为(6,2)
把(6,2)代入 y=,得k=12,
则反比例函数的解析式为:y=,
同理,△AOB≌△DGC,
∴CG=OB=4,DG=OA=2,
则OF=4,CF=6,
把x=4代入y=,得y=3,
∴m=6﹣3=3
∴将正方形向下平移3个单位后,点C刚好落在双曲线上,
故答案为:3.
【点评】本题考查的是反比例函数与一次函数的交点问题、坐标与图形变化﹣平移问题、正方形的性质,掌握待定系数法求函数解析式的一般步骤、平移的性质是解题的关键.
5.一组有序排列的数具有如下规律:任意相邻的三个数,中间的数等于前后两数的积.若这组数第1个数是a,第5个数是,则第2028个数是 (用含a的式子表示).
【分析】设第2个数为x,第3个数为y,第4个数为z,根据任意相邻的三个数,中间的数等于前后两数的积,求出x,y,z,进而得到这组数每6个一组进行循环,进一步求出第2028个数即可.
【解答】解:设第2个数为x,第3个数为y,第4个数为z,由题意,得:,
∴,
∴这组数据为,即:这组数以6个为一组,进行循环,
∵2028÷6=338,
∴第2028个数是;
故答案为:.
【点评】本题考查数字类规律探究,解题的关键是找到规律.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
