浙江省中考数学考前冲刺每日一练10(精选全省各市历年经典真题,包含常考题型、易错题型、 小压轴、大压轴)
文档属性
| 名称 | 浙江省中考数学考前冲刺每日一练10(精选全省各市历年经典真题,包含常考题型、易错题型、 小压轴、大压轴) |  | |
| 格式 | doc | ||
| 文件大小 | 425.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-24 09:27:45 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
浙江省中考数学考前冲刺每日一练10(精选全省各市历年经典真题,包含常考题型、易错题型、 小压轴、大压轴)
1.已知=( )
A. B. C. D.1
2.如图,以AB为直径的半圆中,有一内接正方形CDEF,其边长为1,AC=a,BC=b,则的值为( )
A. B.3 C. D.
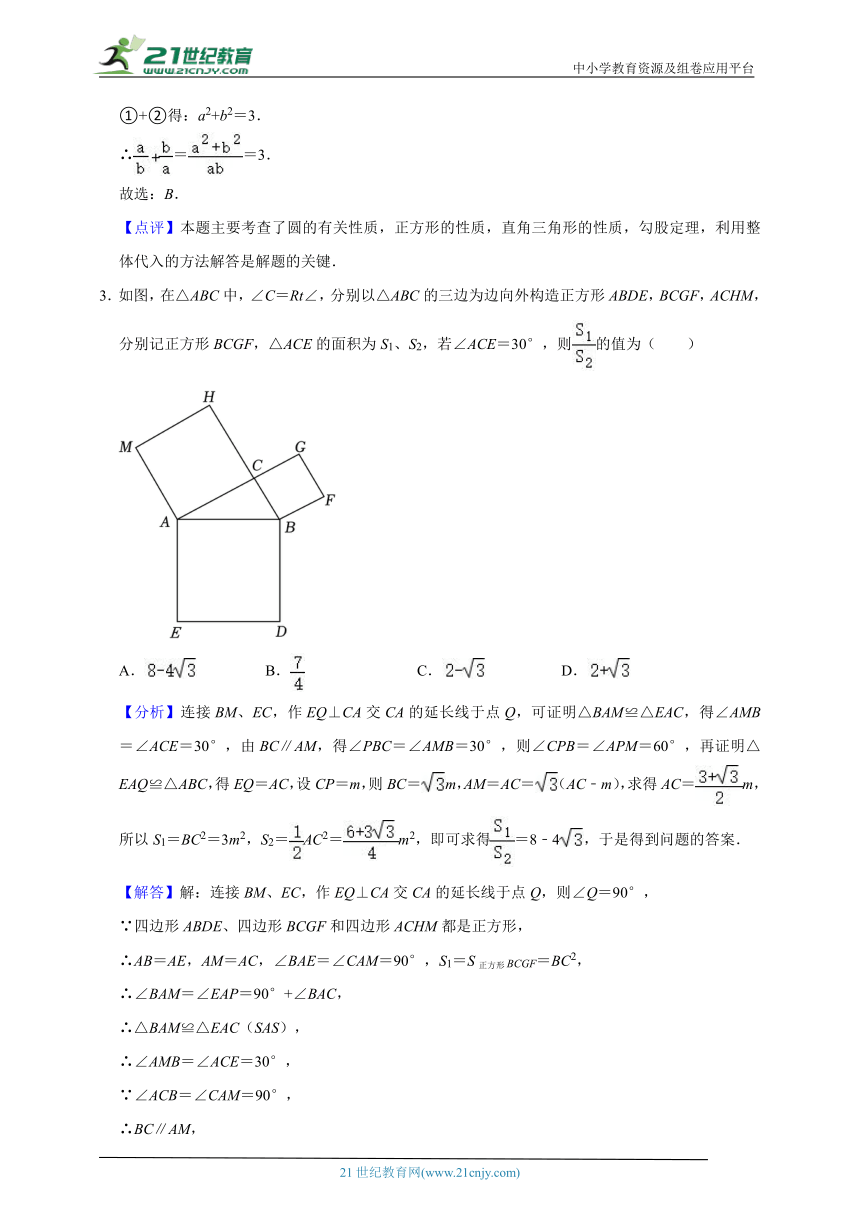
3.如图,在△ABC中,∠C=Rt∠,分别以△ABC的三边为边向外构造正方形ABDE,BCGF,ACHM,分别记正方形BCGF,△ACE的面积为S1、S2,若∠ACE=30°,则的值为( )
A. B. C. D.
4.已知二次函数y=ax2+bx+c(a≠0)图象上部分点的坐标(x,y)对应值列表如下:
x … 0 500 2000 …
y … 1 ﹣1 1 …
则关于x的方程ax2+bx+2=0的解是 .
5.【问题背景】
水火箭是一种基于水和压缩空气的简易火箭,通常由塑胶汽水瓶作为火箭的箭身,并把水当作喷射剂.图1是某学校兴趣小组制做出的一款简易弹射水火箭.
【实验操作】
为验证水火箭的一些性能,兴趣小组同学通过测试收集了水火箭相对于出发点的水平距离x(单位:m)与飞行时间t(单位:s)的数据,并确定了函数表达式为:x=3t.同时也收集了飞行高度y(单位:m)与飞行时间t(单位:s)的数据,发现其近似满足二次函数关系.数据如表所示:
飞行时间t/s 0 2 4 6 8 …
飞行高度y/m 0 10 16 18 16 …
【建立模型】
任务1:求y关于t的函数表达式.
【反思优化】
图2是兴趣小组同学在室内操场的水平地面上设置一个高度可以变化的发射平台(距离地面的高度为PQ),当弹射高度变化时,水火箭飞行的轨迹可视为抛物线上下平移得到,线段AB为水火箭回收区域,已知AP=42m,.
任务2:探究飞行距离,当水火箭落地(高度为0m)时,求水火箭飞行的水平距离.
任务3:当水火箭落到AB内(包括端点A,B),求发射台高度PQ的取值范围.
浙江省中考数学考前冲刺每日一练10(精选全省各市历年经典真题,包含常考题型、易错题型、 小压轴、大压轴)参考答案与试题解析
一.选择题(共3小题)
1.已知=( )
A. B. C. D.1
【分析】围绕已知等式变形,分别求c及,再求c+的值.
【解答】解:∵,
∴,即
,即
∴.
故选:D.
【点评】本题考查了分式等式的变形方法,分式的加减运算,需要灵活掌握.
2.如图,以AB为直径的半圆中,有一内接正方形CDEF,其边长为1,AC=a,BC=b,则的值为( )
A. B.3 C. D.
【分析】利用圆的有关性质,正方形的性质和直角三角形的性质,勾股定理求得ab,a+b的值,再利用整体代入的方法解答即可.
【解答】解:∵以AB为直径的半圆中,有一内接正方形CDEF,其边长为1,
∴a+b=AC+CB=AB=2OD,OC=OF=FC=,CD=1.
∵OC2+CD2=OD2,
∴OD==.
∴a+b=.
∴a2+2ab+b2=5①.
∵OC=OB﹣BC=﹣b==,
∴a﹣b=1.
∴a2﹣2ab+b2=1②.
∴①﹣②得:4ab=4,
∴ab=1.
①+②得:a2+b2=3.
∴==3.
故选:B.
【点评】本题主要考查了圆的有关性质,正方形的性质,直角三角形的性质,勾股定理,利用整体代入的方法解答是解题的关键.
3.如图,在△ABC中,∠C=Rt∠,分别以△ABC的三边为边向外构造正方形ABDE,BCGF,ACHM,分别记正方形BCGF,△ACE的面积为S1、S2,若∠ACE=30°,则的值为( )
A. B. C. D.
【分析】连接BM、EC,作EQ⊥CA交CA的延长线于点Q,可证明△BAM≌△EAC,得∠AMB=∠ACE=30°,由BC∥AM,得∠PBC=∠AMB=30°,则∠CPB=∠APM=60°,再证明△EAQ≌△ABC,得EQ=AC,设CP=m,则BC=m,AM=AC=(AC﹣m),求得AC=m,所以S1=BC2=3m2,S2=AC2=m2,即可求得=8﹣4,于是得到问题的答案.
【解答】解:连接BM、EC,作EQ⊥CA交CA的延长线于点Q,则∠Q=90°,
∵四边形ABDE、四边形BCGF和四边形ACHM都是正方形,
∴AB=AE,AM=AC,∠BAE=∠CAM=90°,S1=S正方形BCGF=BC2,
∴∠BAM=∠EAP=90°+∠BAC,
∴△BAM≌△EAC(SAS),
∴∠AMB=∠ACE=30°,
∵∠ACB=∠CAM=90°,
∴BC∥AM,
∴∠PBC=∠AMB=30°,
∴∠CPB=∠APM=90°﹣30°=60°,
∵∠Q=∠ACB=90°,∠AEQ=∠BAC=90°﹣∠QAE,EA=AB,
∴△EAQ≌△ABC(AAS),
∴EQ=AC,
∴S2=S△ACE=AC EQ=AC2,
∴设CP=m,则AP=AC﹣m,
∵=tan∠CPB=tan60°=,==tan∠APM=tan60°=,
∴BC=CP=m,AC=AP=(AC﹣m),
∴AC=m,
∴S1=BC2=(m)2=3m2,S2=AC2=×(m)2=m2,
∴==8﹣4,
故选:A.
【点评】此题重点考查正方形的性质、同角的余角相等、全等三角形的判定与性质、锐角三角函数与解直角三角形、三角形的面积公式等知识,正确地作出辅助线是解题的关键.
二.填空题(共1小题)
4.已知二次函数y=ax2+bx+c(a≠0)图象上部分点的坐标(x,y)对应值列表如下:
x … 0 500 2000 …
y … 1 ﹣1 1 …
则关于x的方程ax2+bx+2=0的解是 500或1500 .
【分析】根据表格中的数据,可以得到该函数的对称轴和c的值,从而可以得到x=0和x=2000时对应的函数值都是1,再将x=500,y=﹣1代入函数解析式,整理可以得到方程ax2+bx+2=0,从而可以得到该方程的解.
【解答】解:由表格可知,
二次函数y=ax2+bx+c(a≠0)的对称轴是直线x=(2000+0)=1000,
则x=0和x=2000时对应的函数值都是1,
当x=0时,y=1,即c=1,
所以,当x=500时,y=﹣1,即﹣1=ax2+bx+1,
整理,得ax2+bx+2=0,
则方程ax2+bx+2=0的解是x1=500,x2=1500,
故答案为:500或1500.
【点评】本题考查抛物线与x轴的交点、二次函数图象上点的坐标特征、二次函数与一元二次方程的关系,解答本题的关键是明确题意,利用二次函数的性质解答.
三.解答题(共1小题)
5.【问题背景】
水火箭是一种基于水和压缩空气的简易火箭,通常由塑胶汽水瓶作为火箭的箭身,并把水当作喷射剂.图1是某学校兴趣小组制做出的一款简易弹射水火箭.
【实验操作】
为验证水火箭的一些性能,兴趣小组同学通过测试收集了水火箭相对于出发点的水平距离x(单位:m)与飞行时间t(单位:s)的数据,并确定了函数表达式为:x=3t.同时也收集了飞行高度y(单位:m)与飞行时间t(单位:s)的数据,发现其近似满足二次函数关系.数据如表所示:
飞行时间t/s 0 2 4 6 8 …
飞行高度y/m 0 10 16 18 16 …
【建立模型】
任务1:求y关于t的函数表达式.
【反思优化】
图2是兴趣小组同学在室内操场的水平地面上设置一个高度可以变化的发射平台(距离地面的高度为PQ),当弹射高度变化时,水火箭飞行的轨迹可视为抛物线上下平移得到,线段AB为水火箭回收区域,已知AP=42m,.
任务2:探究飞行距离,当水火箭落地(高度为0m)时,求水火箭飞行的水平距离.
任务3:当水火箭落到AB内(包括端点A,B),求发射台高度PQ的取值范围.
【分析】任务1:易得抛物线的顶点坐标为(6,18),用顶点式设出抛物线解析式,把(0,0)代入后可求得a的值,即可求得抛物线解析式;
任务2:用含x的式子表示出t,代入任务1得到的函数解析式可得y关于x的函数解析式,水火箭落地,那么高度为0,函数值取0可求得相应的x的值,找到符合题意的解即可;
任务3:设PQ的长度为c.那么水火箭的抛物线解析式为y=﹣x2+2x+c.把点A、B的坐标代入函数解析式可得c的值,进而可得c也就是PQ的取值范围.
【解答】解:任务1:∵二次函数经过点(4,16),(8,16),
∴抛物线的顶点坐标为(6,18).
设抛物线解析式为:y=a(t﹣6)2+18.
∵抛物线经过点(0,0),
∴36a+18=0.
解得:a=﹣.
∴y关于t的函数表达式为:y=﹣(t﹣6)2+18;
任务2:∵x=3t,
∴t=.
∴y=﹣(﹣6)2+18
=﹣x2+2x.
当水火箭落地(高度为0m)时,﹣x2+2x=0.
解得:x1=0(不合题意,舍去),x2=36.
答:水火箭飞行的水平距离为36米;
任务3:设PQ的长度为c.
∴水火箭的抛物线解析式为y=﹣x2+2x+c.
①当抛物线经过点A时.
∵AP=42m,
∴点A的坐标为(42,0).
∴﹣×422+2×42+c=0.
解得:c=14.
②当抛物线经过点B时.
∵AP=42m,.
∴BP=(18+18)m.
∴点B的坐标为(18+18,0).
∴﹣×(18+18)2+2×(18+18)+c=0.
解得:c=18.
∵水火箭落到AB内(包括端点A,B),
∴14m≤c≤18m.
∴14m≤PQ≤18m.
答:发射台高度PQ的取值范围为:14m≤PQ≤18m.
【点评】本题考查二次函数的应用.用到的知识点为:二次函数经过点(x1,y),(x2,y),抛物线的对称轴为直线x=;二次函数上下平移,只改变常数项,上加下减.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
浙江省中考数学考前冲刺每日一练10(精选全省各市历年经典真题,包含常考题型、易错题型、 小压轴、大压轴)
1.已知=( )
A. B. C. D.1
2.如图,以AB为直径的半圆中,有一内接正方形CDEF,其边长为1,AC=a,BC=b,则的值为( )
A. B.3 C. D.
3.如图,在△ABC中,∠C=Rt∠,分别以△ABC的三边为边向外构造正方形ABDE,BCGF,ACHM,分别记正方形BCGF,△ACE的面积为S1、S2,若∠ACE=30°,则的值为( )
A. B. C. D.
4.已知二次函数y=ax2+bx+c(a≠0)图象上部分点的坐标(x,y)对应值列表如下:
x … 0 500 2000 …
y … 1 ﹣1 1 …
则关于x的方程ax2+bx+2=0的解是 .
5.【问题背景】
水火箭是一种基于水和压缩空气的简易火箭,通常由塑胶汽水瓶作为火箭的箭身,并把水当作喷射剂.图1是某学校兴趣小组制做出的一款简易弹射水火箭.
【实验操作】
为验证水火箭的一些性能,兴趣小组同学通过测试收集了水火箭相对于出发点的水平距离x(单位:m)与飞行时间t(单位:s)的数据,并确定了函数表达式为:x=3t.同时也收集了飞行高度y(单位:m)与飞行时间t(单位:s)的数据,发现其近似满足二次函数关系.数据如表所示:
飞行时间t/s 0 2 4 6 8 …
飞行高度y/m 0 10 16 18 16 …
【建立模型】
任务1:求y关于t的函数表达式.
【反思优化】
图2是兴趣小组同学在室内操场的水平地面上设置一个高度可以变化的发射平台(距离地面的高度为PQ),当弹射高度变化时,水火箭飞行的轨迹可视为抛物线上下平移得到,线段AB为水火箭回收区域,已知AP=42m,.
任务2:探究飞行距离,当水火箭落地(高度为0m)时,求水火箭飞行的水平距离.
任务3:当水火箭落到AB内(包括端点A,B),求发射台高度PQ的取值范围.
浙江省中考数学考前冲刺每日一练10(精选全省各市历年经典真题,包含常考题型、易错题型、 小压轴、大压轴)参考答案与试题解析
一.选择题(共3小题)
1.已知=( )
A. B. C. D.1
【分析】围绕已知等式变形,分别求c及,再求c+的值.
【解答】解:∵,
∴,即
,即
∴.
故选:D.
【点评】本题考查了分式等式的变形方法,分式的加减运算,需要灵活掌握.
2.如图,以AB为直径的半圆中,有一内接正方形CDEF,其边长为1,AC=a,BC=b,则的值为( )
A. B.3 C. D.
【分析】利用圆的有关性质,正方形的性质和直角三角形的性质,勾股定理求得ab,a+b的值,再利用整体代入的方法解答即可.
【解答】解:∵以AB为直径的半圆中,有一内接正方形CDEF,其边长为1,
∴a+b=AC+CB=AB=2OD,OC=OF=FC=,CD=1.
∵OC2+CD2=OD2,
∴OD==.
∴a+b=.
∴a2+2ab+b2=5①.
∵OC=OB﹣BC=﹣b==,
∴a﹣b=1.
∴a2﹣2ab+b2=1②.
∴①﹣②得:4ab=4,
∴ab=1.
①+②得:a2+b2=3.
∴==3.
故选:B.
【点评】本题主要考查了圆的有关性质,正方形的性质,直角三角形的性质,勾股定理,利用整体代入的方法解答是解题的关键.
3.如图,在△ABC中,∠C=Rt∠,分别以△ABC的三边为边向外构造正方形ABDE,BCGF,ACHM,分别记正方形BCGF,△ACE的面积为S1、S2,若∠ACE=30°,则的值为( )
A. B. C. D.
【分析】连接BM、EC,作EQ⊥CA交CA的延长线于点Q,可证明△BAM≌△EAC,得∠AMB=∠ACE=30°,由BC∥AM,得∠PBC=∠AMB=30°,则∠CPB=∠APM=60°,再证明△EAQ≌△ABC,得EQ=AC,设CP=m,则BC=m,AM=AC=(AC﹣m),求得AC=m,所以S1=BC2=3m2,S2=AC2=m2,即可求得=8﹣4,于是得到问题的答案.
【解答】解:连接BM、EC,作EQ⊥CA交CA的延长线于点Q,则∠Q=90°,
∵四边形ABDE、四边形BCGF和四边形ACHM都是正方形,
∴AB=AE,AM=AC,∠BAE=∠CAM=90°,S1=S正方形BCGF=BC2,
∴∠BAM=∠EAP=90°+∠BAC,
∴△BAM≌△EAC(SAS),
∴∠AMB=∠ACE=30°,
∵∠ACB=∠CAM=90°,
∴BC∥AM,
∴∠PBC=∠AMB=30°,
∴∠CPB=∠APM=90°﹣30°=60°,
∵∠Q=∠ACB=90°,∠AEQ=∠BAC=90°﹣∠QAE,EA=AB,
∴△EAQ≌△ABC(AAS),
∴EQ=AC,
∴S2=S△ACE=AC EQ=AC2,
∴设CP=m,则AP=AC﹣m,
∵=tan∠CPB=tan60°=,==tan∠APM=tan60°=,
∴BC=CP=m,AC=AP=(AC﹣m),
∴AC=m,
∴S1=BC2=(m)2=3m2,S2=AC2=×(m)2=m2,
∴==8﹣4,
故选:A.
【点评】此题重点考查正方形的性质、同角的余角相等、全等三角形的判定与性质、锐角三角函数与解直角三角形、三角形的面积公式等知识,正确地作出辅助线是解题的关键.
二.填空题(共1小题)
4.已知二次函数y=ax2+bx+c(a≠0)图象上部分点的坐标(x,y)对应值列表如下:
x … 0 500 2000 …
y … 1 ﹣1 1 …
则关于x的方程ax2+bx+2=0的解是 500或1500 .
【分析】根据表格中的数据,可以得到该函数的对称轴和c的值,从而可以得到x=0和x=2000时对应的函数值都是1,再将x=500,y=﹣1代入函数解析式,整理可以得到方程ax2+bx+2=0,从而可以得到该方程的解.
【解答】解:由表格可知,
二次函数y=ax2+bx+c(a≠0)的对称轴是直线x=(2000+0)=1000,
则x=0和x=2000时对应的函数值都是1,
当x=0时,y=1,即c=1,
所以,当x=500时,y=﹣1,即﹣1=ax2+bx+1,
整理,得ax2+bx+2=0,
则方程ax2+bx+2=0的解是x1=500,x2=1500,
故答案为:500或1500.
【点评】本题考查抛物线与x轴的交点、二次函数图象上点的坐标特征、二次函数与一元二次方程的关系,解答本题的关键是明确题意,利用二次函数的性质解答.
三.解答题(共1小题)
5.【问题背景】
水火箭是一种基于水和压缩空气的简易火箭,通常由塑胶汽水瓶作为火箭的箭身,并把水当作喷射剂.图1是某学校兴趣小组制做出的一款简易弹射水火箭.
【实验操作】
为验证水火箭的一些性能,兴趣小组同学通过测试收集了水火箭相对于出发点的水平距离x(单位:m)与飞行时间t(单位:s)的数据,并确定了函数表达式为:x=3t.同时也收集了飞行高度y(单位:m)与飞行时间t(单位:s)的数据,发现其近似满足二次函数关系.数据如表所示:
飞行时间t/s 0 2 4 6 8 …
飞行高度y/m 0 10 16 18 16 …
【建立模型】
任务1:求y关于t的函数表达式.
【反思优化】
图2是兴趣小组同学在室内操场的水平地面上设置一个高度可以变化的发射平台(距离地面的高度为PQ),当弹射高度变化时,水火箭飞行的轨迹可视为抛物线上下平移得到,线段AB为水火箭回收区域,已知AP=42m,.
任务2:探究飞行距离,当水火箭落地(高度为0m)时,求水火箭飞行的水平距离.
任务3:当水火箭落到AB内(包括端点A,B),求发射台高度PQ的取值范围.
【分析】任务1:易得抛物线的顶点坐标为(6,18),用顶点式设出抛物线解析式,把(0,0)代入后可求得a的值,即可求得抛物线解析式;
任务2:用含x的式子表示出t,代入任务1得到的函数解析式可得y关于x的函数解析式,水火箭落地,那么高度为0,函数值取0可求得相应的x的值,找到符合题意的解即可;
任务3:设PQ的长度为c.那么水火箭的抛物线解析式为y=﹣x2+2x+c.把点A、B的坐标代入函数解析式可得c的值,进而可得c也就是PQ的取值范围.
【解答】解:任务1:∵二次函数经过点(4,16),(8,16),
∴抛物线的顶点坐标为(6,18).
设抛物线解析式为:y=a(t﹣6)2+18.
∵抛物线经过点(0,0),
∴36a+18=0.
解得:a=﹣.
∴y关于t的函数表达式为:y=﹣(t﹣6)2+18;
任务2:∵x=3t,
∴t=.
∴y=﹣(﹣6)2+18
=﹣x2+2x.
当水火箭落地(高度为0m)时,﹣x2+2x=0.
解得:x1=0(不合题意,舍去),x2=36.
答:水火箭飞行的水平距离为36米;
任务3:设PQ的长度为c.
∴水火箭的抛物线解析式为y=﹣x2+2x+c.
①当抛物线经过点A时.
∵AP=42m,
∴点A的坐标为(42,0).
∴﹣×422+2×42+c=0.
解得:c=14.
②当抛物线经过点B时.
∵AP=42m,.
∴BP=(18+18)m.
∴点B的坐标为(18+18,0).
∴﹣×(18+18)2+2×(18+18)+c=0.
解得:c=18.
∵水火箭落到AB内(包括端点A,B),
∴14m≤c≤18m.
∴14m≤PQ≤18m.
答:发射台高度PQ的取值范围为:14m≤PQ≤18m.
【点评】本题考查二次函数的应用.用到的知识点为:二次函数经过点(x1,y),(x2,y),抛物线的对称轴为直线x=;二次函数上下平移,只改变常数项,上加下减.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
