浙江省中考数学考前冲刺每日一练11(精选全省各市历年经典真题,包含常考题型、易错题型、 小压轴、大压轴)
文档属性
| 名称 | 浙江省中考数学考前冲刺每日一练11(精选全省各市历年经典真题,包含常考题型、易错题型、 小压轴、大压轴) |  | |
| 格式 | doc | ||
| 文件大小 | 525.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-24 09:27:45 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
浙江省中考数学考前冲刺每日一练11(精选全省各市历年经典真题,包含常考题型、易错题型、 小压轴、大压轴)
1.如图,Rt△ABC中,∠ACB=90°,AC=6,BC=8,D是AB的中点,E是BC的中点,EF⊥CD于点F,则EF的长是( )
A.3 B.4 C.5 D.
2.抛物线y=x2+bx+3的对称轴为直线x=1.若关于x的一元二次方程x2+bx+3﹣t=0(t为实数)在﹣1<x<4的范围内有实数根,则t的取值范围是( )
A.2≤t<11 B.t≥2 C.6<t<11 D.2≤t<6
3.如图,在平面直角坐标系中,Rt△AOB斜边上的中点C在y轴正半轴上,M为AC的中点.反比例函数的图象经过点A,M,延长MO交函数在第四象限的图象于点N.反比例函数的图象经过点B,连结BN.若△BMN的面积为18,则m﹣n的值为 .
4.图1,图2都是由边长为1的小正三角形构成的网格,每个网格图中有3个小正三角形已涂上阴影.请在余下的空白小正三角形中,分别按下列要求选取1个涂上阴影:
(1)使得4个阴影小正三角形组成一个轴对称图形.
(2)使得4个阴影小正三角形组成一个中心对称图形.
(请将两个小题依次作答在图1,图2中,均只需画出符合条件的一种情形)
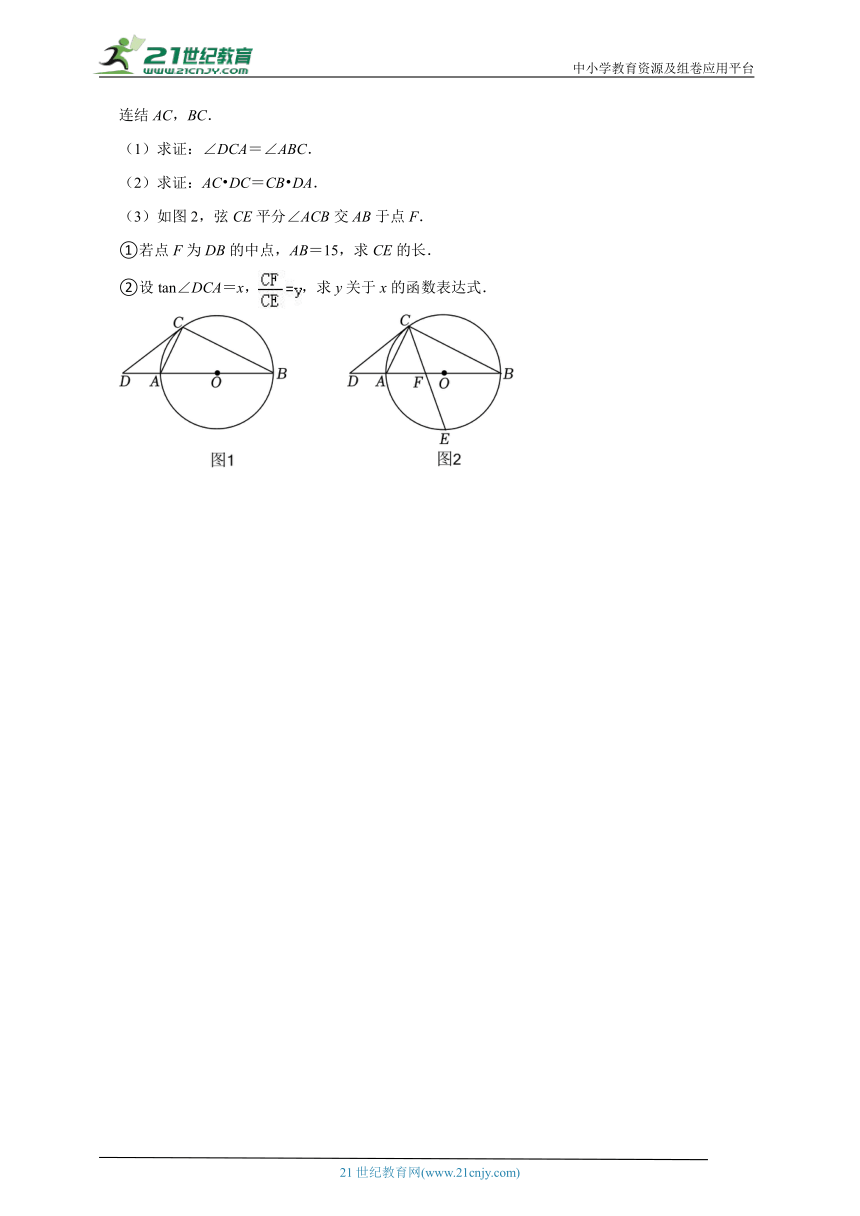
5.如图1,AB是⊙O的直径,点C是⊙O上一点,过点C作⊙O的切线CD交BA的延长线于点D,连结AC,BC.
(1)求证:∠DCA=∠ABC.
(2)求证:AC DC=CB DA.
(3)如图2,弦CE平分∠ACB交AB于点F.
①若点F为DB的中点,AB=15,求CE的长.
②设tan∠DCA=x,,求y关于x的函数表达式.
浙江省中考数学考前冲刺每日一练11(精选全省各市历年经典真题,包含常考题型、易错题型、 小压轴、大压轴)参考答案与试题解析
一.选择题(共2小题)
1.如图,Rt△ABC中,∠ACB=90°,AC=6,BC=8,D是AB的中点,E是BC的中点,EF⊥CD于点F,则EF的长是( )
A.3 B.4 C.5 D.
【分析】根据勾股定理得出AB,进而利用直角三角形的性质得出BD=DC=AD=5,利用三角形面积公式解答即可.
【解答】解:在Rt△ABC中,
∵∠ACB=90°,AC=6,BC=8,
∴AB===10,
∵D是AB的中点,
∴线段CD是中线,
∴AD=BD=CD=5,△BDC=S△ABC=××6×8=12.
如图,连接DE,
∵E为BC边的中点,
∴S△DEC=S△BDC=6,
∵S△DEC=DC EF,
∴×5EF=6,
解得:EF=,
故选:D.
【点评】此题考查勾股定理,直角三角形斜边上的中线,关键是根据勾股定理得出AB,进而利用直角三角形的性质得出BD=DC=AD=5解答.
2.抛物线y=x2+bx+3的对称轴为直线x=1.若关于x的一元二次方程x2+bx+3﹣t=0(t为实数)在﹣1<x<4的范围内有实数根,则t的取值范围是( )
A.2≤t<11 B.t≥2 C.6<t<11 D.2≤t<6
【分析】根据给出的对称轴求出函数解析式为y=x2﹣2x+3,将一元二次方程x2+bx+3﹣t=0的实数根可以看作y=x2﹣2x+3与函数y=t的图象有交点,再由﹣1<x<4的范围确定y的取值范围即可求解.
【解答】解:∵y=x2+bx+3的对称轴为直线x=1,
∴b=﹣2,
∴y=x2﹣2x+3,
∴一元二次方程x2+bx+3﹣t=0的实数根可以看作y=x2﹣2x+3与函数y=t的图象有交点,
∵方程在﹣1<x<4的范围内有实数根,
当x=﹣1时,y=6;
当x=4时,y=11;
函数y=x2﹣2x+3在x=1时有最小值2;
∴2≤t<11.
故选:A.
【点评】本题考查二次函数的图象及性质;能够将方程的实数根问题转化为二次函数与直线的交点问题,借助数形结合解题是关键.
二.填空题(共1小题)
3.如图,在平面直角坐标系中,Rt△AOB斜边上的中点C在y轴正半轴上,M为AC的中点.反比例函数的图象经过点A,M,延长MO交函数在第四象限的图象于点N.反比例函数的图象经过点B,连结BN.若△BMN的面积为18,则m﹣n的值为 ﹣24 .
【分析】根据三角形中线平分三角形面积,求出三角形AOC和三角形BOC的面积都是6,在证明△ACD和△BCE全等,利用反比例函数的几何意义,表示出△AOD和△BOE的面积,再利用面积差求出m﹣n即可.
【解答】解:作BE⊥y轴于E,AD⊥x轴于D,
∵M,N关于O对称,则MO=NO,
∵△BMN的面积为18,
∴S△BMO=9,
∵点M为AC的中点,
∴MC=AC=BC,
∴S△BOM=3S△COM,
∴S△MOC=3,
∴S△AOC=S△BOC=6,
∵C是AB的中点,
∴AC=BC,
∵∠ADC=∠BEC=90°,∠BCE=∠ACG,
∴△ACD≌△BCE(AAS),
∴S△ACD=S△BCE,
即S△AOC﹣S△AOD=S△BOE﹣S△BOC,
∵S△AOD=,S△BOE=,
∴,
∴m﹣n=﹣24,
故答案为:﹣24.
【点评】本题考查了反比例函数的几何意义的应用,三角形中线平分面积的应用、三角形的全等的应用是解题关键.
三.解答题(共2小题)
4.图1,图2都是由边长为1的小正三角形构成的网格,每个网格图中有3个小正三角形已涂上阴影.请在余下的空白小正三角形中,分别按下列要求选取1个涂上阴影:
(1)使得4个阴影小正三角形组成一个轴对称图形.
(2)使得4个阴影小正三角形组成一个中心对称图形.
(请将两个小题依次作答在图1,图2中,均只需画出符合条件的一种情形)
【分析】(1)根据轴对称图形的定义画出图形即可(答案不唯一);
(2)根据中心对称图形的定义画出图形即可(答案不唯一).
【解答】解:(1)轴对称图形如图所示(答案不唯一);
(2)中心对称图形如图所示(答案不唯一).
【点评】本题考查利用旋转设计图案,利用轴对称设计图案,理解题意,灵活运用所学知识是解决问题的关键.
5.如图1,AB是⊙O的直径,点C是⊙O上一点,过点C作⊙O的切线CD交BA的延长线于点D,连结AC,BC.
(1)求证:∠DCA=∠ABC.
(2)求证:AC DC=CB DA.
(3)如图2,弦CE平分∠ACB交AB于点F.
①若点F为DB的中点,AB=15,求CE的长.
②设tan∠DCA=x,,求y关于x的函数表达式.
【分析】(1)根据切线的性质及圆周角定理推出∠DCA=∠BCO,根据等腰三角形的性质得出∠ABC=∠BCO,等量代换即可得解;
(2)根据相似三角形的判定与性质求解即可;
(3)①连结OE,BE,根据角平分线定义及圆周角定理推出,结合(2),根据相似三角形的性质推出DF=DC=10,AF=5,根据勾股定理推出AB=15,,,根据圆周角定理推出△OBE是等腰直角三角形,则,根据题意推出△ACF∽△ECB,根据相似三角形的性质即可得解;
②由(1)得,设CB=t,则AC=xt,根据勾股定理推出,根据相似三角形的判定与性质求解即可.
【解答】(1)证明:连结OC.
∵DC是⊙O的切线,
∴∠DCO=90°,
即∠DCA+∠ACO=∠DCO=90°,
∵AB是⊙O的直径,
∴∠ACB=90°,
即∠BCO+∠ACO=∠ACB=90°,
∴∠DCA=∠BCO,
∵OC=OB,
∴∠ABC=∠BCO,
∴∠DCA=∠ABC;
(2)证明:由(1)得∠DCA=∠ABC,
∵∠D=∠D,
∴△ACD∽△CBD,
∴,
∴AC DC=CB DA.
(3)解:①连结OE,BE.
∵弦CE平分∠ACB,∠ACB=90°,
∴,
∵∠DCA=∠ABC,
∴∠DCA+∠ACF=∠FCB+∠ABC,
即∠DCF=∠DFC,
∴DC=DF,
∵点F为DB的中点,
∴,
由(2)得△ACD∽△CBD,
∴==,
即,
∴,
∴,
∴DF=DC=10,
∴AF=5,
∵,
∵AC2+BC2=AB2,
∴,
∵AB=15,
∴,,
∵∠ECB=45°,
∴∠EOB=2∠ECB=90°,
∵OE=OB=,
∴△OEB是等腰直角三角形,
∴,
∵∠ACF=∠ECB,∠CAF=∠CEB,
∴△ACF∽△ECB,
∴,
∴CE==;
②∵∠ACB=90°,∠ABC=∠DCA,
∴,
设CB=t,则AC=xt,
∴AB2=AC2+CB2=(xt)2+t2=(x2+1)t2,
∴,
∵∠BEF=∠CEB,∠EBF=∠ACF=∠BCE,
∴△EBF∽△ECB,
∴,
∴EB2=EC EF,
∵△ACF∽△ECB,
∴,
∴AC CB=EC CF,
∴,
∴,
∴y=.
【点评】此题是圆的综合题,考查了切线的性质、圆周角定理、相似三角形的判定与性质、勾股定理、锐角三角函数等知识,熟练掌握切线的性质、圆周角定理、相似三角形的判定与性质、勾股定理、锐角三角函数等知识并作出合理的辅助线是解题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
浙江省中考数学考前冲刺每日一练11(精选全省各市历年经典真题,包含常考题型、易错题型、 小压轴、大压轴)
1.如图,Rt△ABC中,∠ACB=90°,AC=6,BC=8,D是AB的中点,E是BC的中点,EF⊥CD于点F,则EF的长是( )
A.3 B.4 C.5 D.
2.抛物线y=x2+bx+3的对称轴为直线x=1.若关于x的一元二次方程x2+bx+3﹣t=0(t为实数)在﹣1<x<4的范围内有实数根,则t的取值范围是( )
A.2≤t<11 B.t≥2 C.6<t<11 D.2≤t<6
3.如图,在平面直角坐标系中,Rt△AOB斜边上的中点C在y轴正半轴上,M为AC的中点.反比例函数的图象经过点A,M,延长MO交函数在第四象限的图象于点N.反比例函数的图象经过点B,连结BN.若△BMN的面积为18,则m﹣n的值为 .
4.图1,图2都是由边长为1的小正三角形构成的网格,每个网格图中有3个小正三角形已涂上阴影.请在余下的空白小正三角形中,分别按下列要求选取1个涂上阴影:
(1)使得4个阴影小正三角形组成一个轴对称图形.
(2)使得4个阴影小正三角形组成一个中心对称图形.
(请将两个小题依次作答在图1,图2中,均只需画出符合条件的一种情形)
5.如图1,AB是⊙O的直径,点C是⊙O上一点,过点C作⊙O的切线CD交BA的延长线于点D,连结AC,BC.
(1)求证:∠DCA=∠ABC.
(2)求证:AC DC=CB DA.
(3)如图2,弦CE平分∠ACB交AB于点F.
①若点F为DB的中点,AB=15,求CE的长.
②设tan∠DCA=x,,求y关于x的函数表达式.
浙江省中考数学考前冲刺每日一练11(精选全省各市历年经典真题,包含常考题型、易错题型、 小压轴、大压轴)参考答案与试题解析
一.选择题(共2小题)
1.如图,Rt△ABC中,∠ACB=90°,AC=6,BC=8,D是AB的中点,E是BC的中点,EF⊥CD于点F,则EF的长是( )
A.3 B.4 C.5 D.
【分析】根据勾股定理得出AB,进而利用直角三角形的性质得出BD=DC=AD=5,利用三角形面积公式解答即可.
【解答】解:在Rt△ABC中,
∵∠ACB=90°,AC=6,BC=8,
∴AB===10,
∵D是AB的中点,
∴线段CD是中线,
∴AD=BD=CD=5,△BDC=S△ABC=××6×8=12.
如图,连接DE,
∵E为BC边的中点,
∴S△DEC=S△BDC=6,
∵S△DEC=DC EF,
∴×5EF=6,
解得:EF=,
故选:D.
【点评】此题考查勾股定理,直角三角形斜边上的中线,关键是根据勾股定理得出AB,进而利用直角三角形的性质得出BD=DC=AD=5解答.
2.抛物线y=x2+bx+3的对称轴为直线x=1.若关于x的一元二次方程x2+bx+3﹣t=0(t为实数)在﹣1<x<4的范围内有实数根,则t的取值范围是( )
A.2≤t<11 B.t≥2 C.6<t<11 D.2≤t<6
【分析】根据给出的对称轴求出函数解析式为y=x2﹣2x+3,将一元二次方程x2+bx+3﹣t=0的实数根可以看作y=x2﹣2x+3与函数y=t的图象有交点,再由﹣1<x<4的范围确定y的取值范围即可求解.
【解答】解:∵y=x2+bx+3的对称轴为直线x=1,
∴b=﹣2,
∴y=x2﹣2x+3,
∴一元二次方程x2+bx+3﹣t=0的实数根可以看作y=x2﹣2x+3与函数y=t的图象有交点,
∵方程在﹣1<x<4的范围内有实数根,
当x=﹣1时,y=6;
当x=4时,y=11;
函数y=x2﹣2x+3在x=1时有最小值2;
∴2≤t<11.
故选:A.
【点评】本题考查二次函数的图象及性质;能够将方程的实数根问题转化为二次函数与直线的交点问题,借助数形结合解题是关键.
二.填空题(共1小题)
3.如图,在平面直角坐标系中,Rt△AOB斜边上的中点C在y轴正半轴上,M为AC的中点.反比例函数的图象经过点A,M,延长MO交函数在第四象限的图象于点N.反比例函数的图象经过点B,连结BN.若△BMN的面积为18,则m﹣n的值为 ﹣24 .
【分析】根据三角形中线平分三角形面积,求出三角形AOC和三角形BOC的面积都是6,在证明△ACD和△BCE全等,利用反比例函数的几何意义,表示出△AOD和△BOE的面积,再利用面积差求出m﹣n即可.
【解答】解:作BE⊥y轴于E,AD⊥x轴于D,
∵M,N关于O对称,则MO=NO,
∵△BMN的面积为18,
∴S△BMO=9,
∵点M为AC的中点,
∴MC=AC=BC,
∴S△BOM=3S△COM,
∴S△MOC=3,
∴S△AOC=S△BOC=6,
∵C是AB的中点,
∴AC=BC,
∵∠ADC=∠BEC=90°,∠BCE=∠ACG,
∴△ACD≌△BCE(AAS),
∴S△ACD=S△BCE,
即S△AOC﹣S△AOD=S△BOE﹣S△BOC,
∵S△AOD=,S△BOE=,
∴,
∴m﹣n=﹣24,
故答案为:﹣24.
【点评】本题考查了反比例函数的几何意义的应用,三角形中线平分面积的应用、三角形的全等的应用是解题关键.
三.解答题(共2小题)
4.图1,图2都是由边长为1的小正三角形构成的网格,每个网格图中有3个小正三角形已涂上阴影.请在余下的空白小正三角形中,分别按下列要求选取1个涂上阴影:
(1)使得4个阴影小正三角形组成一个轴对称图形.
(2)使得4个阴影小正三角形组成一个中心对称图形.
(请将两个小题依次作答在图1,图2中,均只需画出符合条件的一种情形)
【分析】(1)根据轴对称图形的定义画出图形即可(答案不唯一);
(2)根据中心对称图形的定义画出图形即可(答案不唯一).
【解答】解:(1)轴对称图形如图所示(答案不唯一);
(2)中心对称图形如图所示(答案不唯一).
【点评】本题考查利用旋转设计图案,利用轴对称设计图案,理解题意,灵活运用所学知识是解决问题的关键.
5.如图1,AB是⊙O的直径,点C是⊙O上一点,过点C作⊙O的切线CD交BA的延长线于点D,连结AC,BC.
(1)求证:∠DCA=∠ABC.
(2)求证:AC DC=CB DA.
(3)如图2,弦CE平分∠ACB交AB于点F.
①若点F为DB的中点,AB=15,求CE的长.
②设tan∠DCA=x,,求y关于x的函数表达式.
【分析】(1)根据切线的性质及圆周角定理推出∠DCA=∠BCO,根据等腰三角形的性质得出∠ABC=∠BCO,等量代换即可得解;
(2)根据相似三角形的判定与性质求解即可;
(3)①连结OE,BE,根据角平分线定义及圆周角定理推出,结合(2),根据相似三角形的性质推出DF=DC=10,AF=5,根据勾股定理推出AB=15,,,根据圆周角定理推出△OBE是等腰直角三角形,则,根据题意推出△ACF∽△ECB,根据相似三角形的性质即可得解;
②由(1)得,设CB=t,则AC=xt,根据勾股定理推出,根据相似三角形的判定与性质求解即可.
【解答】(1)证明:连结OC.
∵DC是⊙O的切线,
∴∠DCO=90°,
即∠DCA+∠ACO=∠DCO=90°,
∵AB是⊙O的直径,
∴∠ACB=90°,
即∠BCO+∠ACO=∠ACB=90°,
∴∠DCA=∠BCO,
∵OC=OB,
∴∠ABC=∠BCO,
∴∠DCA=∠ABC;
(2)证明:由(1)得∠DCA=∠ABC,
∵∠D=∠D,
∴△ACD∽△CBD,
∴,
∴AC DC=CB DA.
(3)解:①连结OE,BE.
∵弦CE平分∠ACB,∠ACB=90°,
∴,
∵∠DCA=∠ABC,
∴∠DCA+∠ACF=∠FCB+∠ABC,
即∠DCF=∠DFC,
∴DC=DF,
∵点F为DB的中点,
∴,
由(2)得△ACD∽△CBD,
∴==,
即,
∴,
∴,
∴DF=DC=10,
∴AF=5,
∵,
∵AC2+BC2=AB2,
∴,
∵AB=15,
∴,,
∵∠ECB=45°,
∴∠EOB=2∠ECB=90°,
∵OE=OB=,
∴△OEB是等腰直角三角形,
∴,
∵∠ACF=∠ECB,∠CAF=∠CEB,
∴△ACF∽△ECB,
∴,
∴CE==;
②∵∠ACB=90°,∠ABC=∠DCA,
∴,
设CB=t,则AC=xt,
∴AB2=AC2+CB2=(xt)2+t2=(x2+1)t2,
∴,
∵∠BEF=∠CEB,∠EBF=∠ACF=∠BCE,
∴△EBF∽△ECB,
∴,
∴EB2=EC EF,
∵△ACF∽△ECB,
∴,
∴AC CB=EC CF,
∴,
∴,
∴y=.
【点评】此题是圆的综合题,考查了切线的性质、圆周角定理、相似三角形的判定与性质、勾股定理、锐角三角函数等知识,熟练掌握切线的性质、圆周角定理、相似三角形的判定与性质、勾股定理、锐角三角函数等知识并作出合理的辅助线是解题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
