浙江省中考数学考前冲刺每日一练13(精选全省各市历年经典真题,包含常考题型、易错题型、 小压轴、大压轴)
文档属性
| 名称 | 浙江省中考数学考前冲刺每日一练13(精选全省各市历年经典真题,包含常考题型、易错题型、 小压轴、大压轴) |  | |
| 格式 | doc | ||
| 文件大小 | 396.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-24 09:27:45 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
浙江省中考数学考前冲刺每日一练13(精选全省各市历年经典真题,包含常考题型、易错题型、 小压轴、大压轴)
1.现有3包同一品牌的饼干,其中2包已过期,随机抽取2包,2包都过期的概率是( )
A. B. C. D.
2.如图,二次函数y=ax2+bx+c(a≠0)与x轴交点的横坐标为x1,x2与y轴正半轴的交点为C,一1<x1<0,x2=2,则下列结论正确的是( )
A.b2﹣4ac<0. B.9a+3b+c>0 C.abc>0 D.a+b>0
3.如图,在平面直角坐标系xOy中,矩形ABCO的顶点A,C分别在x轴,y轴的正半轴上,点D,E是CO的两个三等分点,过点D,E作x轴的平行线分别交AB于点F,G,反比例函数y=(x>0)的图象经过点G,分别交BC,DF于点Q,P,分别过点Q,P,作x轴的垂线,垂足分别为H,K.图中阴影部分的面积分别为S1,S2,S3.若OE=HK=1,则点G的坐标为 ;若S1+S3=25,则S2= .
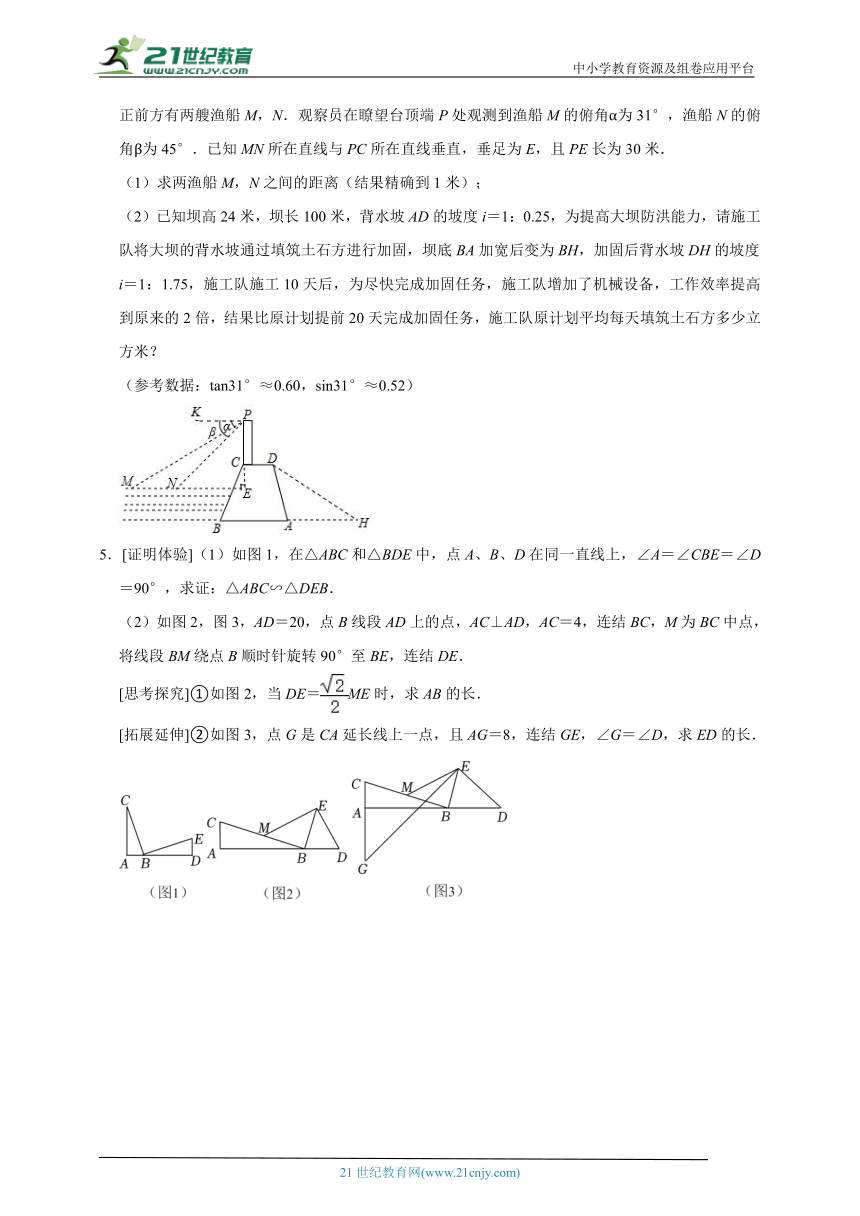
4.某水库大坝的横截面是如图所示的四边形ABCD,其中AB∥CD,大坝顶上有一瞭望台PC,PC正前方有两艘渔船M,N.观察员在瞭望台顶端P处观测到渔船M的俯角α为31°,渔船N的俯角β为45°.已知MN所在直线与PC所在直线垂直,垂足为E,且PE长为30米.
(1)求两渔船M,N之间的距离(结果精确到1米);
(2)已知坝高24米,坝长100米,背水坡AD的坡度i=1:0.25,为提高大坝防洪能力,请施工队将大坝的背水坡通过填筑土石方进行加固,坝底BA加宽后变为BH,加固后背水坡DH的坡度i=1:1.75,施工队施工10天后,为尽快完成加固任务,施工队增加了机械设备,工作效率提高到原来的2倍,结果比原计划提前20天完成加固任务,施工队原计划平均每天填筑土石方多少立方米?
(参考数据:tan31°≈0.60,sin31°≈0.52)
5.[证明体验](1)如图1,在△ABC和△BDE中,点A、B、D在同一直线上,∠A=∠CBE=∠D=90°,求证:△ABC∽△DEB.
(2)如图2,图3,AD=20,点B线段AD上的点,AC⊥AD,AC=4,连结BC,M为BC中点,将线段BM绕点B顺时针旋转90°至BE,连结DE.
[思考探究]①如图2,当DE=ME时,求AB的长.
[拓展延伸]②如图3,点G是CA延长线上一点,且AG=8,连结GE,∠G=∠D,求ED的长.
浙江省中考数学考前冲刺每日一练13(精选全省各市历年经典真题,包含常考题型、易错题型、 小压轴、大压轴)参考答案与试题解析
一.选择题(共2小题)
1.现有3包同一品牌的饼干,其中2包已过期,随机抽取2包,2包都过期的概率是( )
A. B. C. D.
【分析】画树状图,共有6种等可能的结果,2包都过期的结果有2种,再由概率公式求解即可.
【解答】解:把不过期的饼干记为A,2包已过期B,C,
画树状图如图:
共有6种等可能的结果,2包都过期的结果有2种,
∴两盒都不过期的概率为=,
故选:D.
【点评】本题考查的是用列表法或画树状图法求概率.列表法或画树状图法可以不重复不遗漏的列出所有可能的结果,列表法适合于两步完成的事件,树状图法适合两步或两步以上完成的事件.用到的知识点为:概率=所求情况数与总情况数之比.
2.如图,二次函数y=ax2+bx+c(a≠0)与x轴交点的横坐标为x1,x2与y轴正半轴的交点为C,一1<x1<0,x2=2,则下列结论正确的是( )
A.b2﹣4ac<0. B.9a+3b+c>0 C.abc>0 D.a+b>0
【分析】由抛物线的开口方向判断a与0的关系,由抛物线与y轴的交点判断c与0的关系,然后根据对称轴及抛物线与x轴交点情况进行推理,进而对所得结论进行判断.
【解答】解:由图象可知,抛物线与x轴有两个交点,
∴b2﹣4ac>0,
故A错误,不符合题意;
由图象可知当x=3时,y=9a+3b+c<0,
故B错误,不符合题意;
∵抛物线开口方向向下,
∴a<0.
∵抛物线与x轴的交点是(x1,0)和(2,0),其中﹣1<x1<0,
∴对称轴x=﹣>0,
∴b>0.
∵抛物线与y轴交于正半轴,
∴c>0,
∴abc<0,
故C错误,不符合题意;
∵﹣1<x1<0,x2=2,
∴1<x1+x2<2,
∴<<1,
∴﹣>,
∴b>﹣a,
即a+b>0,
故D正确,符合题意.
故选:D.
【点评】本题考查了二次函数图象与系数的关系,主要考查学生根据图形进行推理和辨析的能力,用了数形结合思想,题目比较好,但是难度偏大.
二.填空题(共1小题)
3.如图,在平面直角坐标系xOy中,矩形ABCO的顶点A,C分别在x轴,y轴的正半轴上,点D,E是CO的两个三等分点,过点D,E作x轴的平行线分别交AB于点F,G,反比例函数y=(x>0)的图象经过点G,分别交BC,DF于点Q,P,分别过点Q,P,作x轴的垂线,垂足分别为H,K.图中阴影部分的面积分别为S1,S2,S3.若OE=HK=1,则点G的坐标为 (6,1) ;若S1+S3=25,则S2= 5 .
【分析】若OE=HK=1,根据题意Q(,3),P(,2),G(k,1),进而求得Q(2,3),P(3,2),代入反比例函数y=(x>0)求得k的值,即可求得点G的坐标;
若S1+S3=25,由反比例函数系数k的几何意义可知,3S1=2S1+2S2=S1+S2+S3=k,即可得出S1=2S2,2S1=S2+S3,由S1+S3=25,得出S3=25﹣S1,经过变形得到6S2=S2+25,求得S2=5.
【解答】解:若OE=HK=1,
∵点D,E是CO的两个三等分点,
∴OC=3,PK=2,AG=1,
∴Q(,3),P(,2),G(k,1),
∴==,
∵HK=1,
∴OH=2,OK=3,
∴Q(2,3),P(3,2),
∵点Q,P,G在反比例函数y=(x>0)的图象上,
∴k=2×3=6,
∴G(6,1);
若S1+S3=25,
由反比例函数系数k的几何意义可知,3S1=2S1+2S2=S1+S2+S3=k,
∴S1=2S2,2S1=S2+S3,
∵S1+S3=25,
∴S3=25﹣S1,
∴2S1=S2+25﹣S1,
∴3S1=S2+25,
∴6S2=S2+25,
∴S2=5.
故答案为:(6,1),5.
【点评】本题考查了反比例函数系数k的几何意义,反比例函数图象上点的坐标特征,矩形的性质,熟知反比例函数系数k的几何意义是解题的关键.
三.解答题(共2小题)
4.某水库大坝的横截面是如图所示的四边形ABCD,其中AB∥CD,大坝顶上有一瞭望台PC,PC正前方有两艘渔船M,N.观察员在瞭望台顶端P处观测到渔船M的俯角α为31°,渔船N的俯角β为45°.已知MN所在直线与PC所在直线垂直,垂足为E,且PE长为30米.
(1)求两渔船M,N之间的距离(结果精确到1米);
(2)已知坝高24米,坝长100米,背水坡AD的坡度i=1:0.25,为提高大坝防洪能力,请施工队将大坝的背水坡通过填筑土石方进行加固,坝底BA加宽后变为BH,加固后背水坡DH的坡度i=1:1.75,施工队施工10天后,为尽快完成加固任务,施工队增加了机械设备,工作效率提高到原来的2倍,结果比原计划提前20天完成加固任务,施工队原计划平均每天填筑土石方多少立方米?
(参考数据:tan31°≈0.60,sin31°≈0.52)
【分析】(1)在直角△PEN,利用三角函数即可求得ME的长,根据MN=EM﹣EN求解;
(2)过点D作DN⊥AH于点N,利用三角函数求得AN和AH的长,进而求得△ADH的面积,得到需要填筑的土石方数,再根据结果比原计划提前20天完成,列方程求解.
【解答】解:(1)在直角△PEN中,∠PNE=45°,
∴EN=PE=30m,
在Rt△PME中,∠PME=31°,
∴ME==50(m),
则MN=EM﹣EN=20(m).
答:两渔船M、N之间的距离是20米;
(2)过点D作DQ⊥AH于点Q.
由题意得:tan∠DAB=4,tanH=,
在直角△DAQ中,AQ===6(m),
在直角△DHQ中,HQ===42(m).
故AH=HQ﹣AQ=42﹣6=36(m).
S△ADH=AH DQ=432(m2).
故需要填筑的土石方是V=SL=432×100=43200(m3).
设原计划平均每天填筑xm3,则原计划天完成,则增加机械设备后,现在平均每天填筑2xm3.
根据题意,得:10x+() 2x=43200,
解得:x=864.
经检验x=864是原方程的解.
答:施工队原计划平均每天填筑土石方864立方米.
【点评】本题考查了仰角的定义以及坡度,要求学生能借助仰角构造直角三角形并解直角三角形.
5.[证明体验](1)如图1,在△ABC和△BDE中,点A、B、D在同一直线上,∠A=∠CBE=∠D=90°,求证:△ABC∽△DEB.
(2)如图2,图3,AD=20,点B线段AD上的点,AC⊥AD,AC=4,连结BC,M为BC中点,将线段BM绕点B顺时针旋转90°至BE,连结DE.
[思考探究]①如图2,当DE=ME时,求AB的长.
[拓展延伸]②如图3,点G是CA延长线上一点,且AG=8,连结GE,∠G=∠D,求ED的长.
【分析】(1)利用同角的余角相等得∠C=∠DBE,可证明结论;
(2)①过点E作EF⊥AD,垂足为F,由(1)得△ABC∽△FEB,得,可得答案;
②过点M作AD的垂线交AD于点H,过点E作AD的垂线交AD于点F,过点D作DP⊥AD,过点E作NP⊥DP,交AC的延长线于N,首先利用AAS证明△MHB≌△BFE,得BF=MH=2,EF=BH,设EF=x,则DP=x,BH=AH=x,EP=FD=20﹣2﹣2x=18﹣2x,GN=x+8,AF=2x+2,再由∠GED=∠GAH=90°,由(1)得△NGE∽△PED,得,代入计算即可.
【解答】(1)证明:∵∠A=∠CBE=∠D=90°,
∴∠C+∠CBA=90°,∠CBA+∠DBE=90°,
∴∠C=∠DBE,
∴△ABC∽△DEB;
(2)解:①∵M绕点B顺时针旋转90°至E,M为BC的中点,
∴△BME为等腰直角三角形,,
∴BE=,
又∵DE=,
∴BE=DE,
如图,过点E作EF⊥AD,垂足为F,
则BF=DF,
∵∠A=∠CBE=∠BFE=90°,
由(1)得△ABC∽△FEB,
∴,
∵AC=4,
∴BF=2,
∴AB=AD﹣BF﹣FD=20﹣2﹣2=16;
②如图,过点M作AD的垂线交AD于点H,过点E作AD的垂线交AD于点F,过点D作DP⊥AD,过点E作NP⊥DP,交AC的延长线于N,
∵M为BC的中点,MH∥AC,
∴,
∴MH=,BH=AH,
∵∠MHB=∠MBE=∠BFE=90°,
由(1)得:∠HBM=∠FEB,
∵MB=EB,
∴△MHB≌△BFE(AAS),
∴BF=MH=2,EF=BH,
设EF=x,则DP=x,BH=AH=x,EP=FD=20﹣2﹣2x=18﹣2x,GN=x+8,AF=2x+2,
∵∠G=∠D,
∴∠GED=∠GAH=90°,
由(1)得△NGE∽△PED,
∴,
即,
解得x=6或x=﹣(舍去),
∴FD=18﹣2x=6,
∴ED==6.
【点评】本题是相似形综合题,主要考查了相似三角形的判定与性质,等腰直角三角形的性质,全等三角形的判定与性质,熟练掌握一线三等角基本模型是解题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
浙江省中考数学考前冲刺每日一练13(精选全省各市历年经典真题,包含常考题型、易错题型、 小压轴、大压轴)
1.现有3包同一品牌的饼干,其中2包已过期,随机抽取2包,2包都过期的概率是( )
A. B. C. D.
2.如图,二次函数y=ax2+bx+c(a≠0)与x轴交点的横坐标为x1,x2与y轴正半轴的交点为C,一1<x1<0,x2=2,则下列结论正确的是( )
A.b2﹣4ac<0. B.9a+3b+c>0 C.abc>0 D.a+b>0
3.如图,在平面直角坐标系xOy中,矩形ABCO的顶点A,C分别在x轴,y轴的正半轴上,点D,E是CO的两个三等分点,过点D,E作x轴的平行线分别交AB于点F,G,反比例函数y=(x>0)的图象经过点G,分别交BC,DF于点Q,P,分别过点Q,P,作x轴的垂线,垂足分别为H,K.图中阴影部分的面积分别为S1,S2,S3.若OE=HK=1,则点G的坐标为 ;若S1+S3=25,则S2= .
4.某水库大坝的横截面是如图所示的四边形ABCD,其中AB∥CD,大坝顶上有一瞭望台PC,PC正前方有两艘渔船M,N.观察员在瞭望台顶端P处观测到渔船M的俯角α为31°,渔船N的俯角β为45°.已知MN所在直线与PC所在直线垂直,垂足为E,且PE长为30米.
(1)求两渔船M,N之间的距离(结果精确到1米);
(2)已知坝高24米,坝长100米,背水坡AD的坡度i=1:0.25,为提高大坝防洪能力,请施工队将大坝的背水坡通过填筑土石方进行加固,坝底BA加宽后变为BH,加固后背水坡DH的坡度i=1:1.75,施工队施工10天后,为尽快完成加固任务,施工队增加了机械设备,工作效率提高到原来的2倍,结果比原计划提前20天完成加固任务,施工队原计划平均每天填筑土石方多少立方米?
(参考数据:tan31°≈0.60,sin31°≈0.52)
5.[证明体验](1)如图1,在△ABC和△BDE中,点A、B、D在同一直线上,∠A=∠CBE=∠D=90°,求证:△ABC∽△DEB.
(2)如图2,图3,AD=20,点B线段AD上的点,AC⊥AD,AC=4,连结BC,M为BC中点,将线段BM绕点B顺时针旋转90°至BE,连结DE.
[思考探究]①如图2,当DE=ME时,求AB的长.
[拓展延伸]②如图3,点G是CA延长线上一点,且AG=8,连结GE,∠G=∠D,求ED的长.
浙江省中考数学考前冲刺每日一练13(精选全省各市历年经典真题,包含常考题型、易错题型、 小压轴、大压轴)参考答案与试题解析
一.选择题(共2小题)
1.现有3包同一品牌的饼干,其中2包已过期,随机抽取2包,2包都过期的概率是( )
A. B. C. D.
【分析】画树状图,共有6种等可能的结果,2包都过期的结果有2种,再由概率公式求解即可.
【解答】解:把不过期的饼干记为A,2包已过期B,C,
画树状图如图:
共有6种等可能的结果,2包都过期的结果有2种,
∴两盒都不过期的概率为=,
故选:D.
【点评】本题考查的是用列表法或画树状图法求概率.列表法或画树状图法可以不重复不遗漏的列出所有可能的结果,列表法适合于两步完成的事件,树状图法适合两步或两步以上完成的事件.用到的知识点为:概率=所求情况数与总情况数之比.
2.如图,二次函数y=ax2+bx+c(a≠0)与x轴交点的横坐标为x1,x2与y轴正半轴的交点为C,一1<x1<0,x2=2,则下列结论正确的是( )
A.b2﹣4ac<0. B.9a+3b+c>0 C.abc>0 D.a+b>0
【分析】由抛物线的开口方向判断a与0的关系,由抛物线与y轴的交点判断c与0的关系,然后根据对称轴及抛物线与x轴交点情况进行推理,进而对所得结论进行判断.
【解答】解:由图象可知,抛物线与x轴有两个交点,
∴b2﹣4ac>0,
故A错误,不符合题意;
由图象可知当x=3时,y=9a+3b+c<0,
故B错误,不符合题意;
∵抛物线开口方向向下,
∴a<0.
∵抛物线与x轴的交点是(x1,0)和(2,0),其中﹣1<x1<0,
∴对称轴x=﹣>0,
∴b>0.
∵抛物线与y轴交于正半轴,
∴c>0,
∴abc<0,
故C错误,不符合题意;
∵﹣1<x1<0,x2=2,
∴1<x1+x2<2,
∴<<1,
∴﹣>,
∴b>﹣a,
即a+b>0,
故D正确,符合题意.
故选:D.
【点评】本题考查了二次函数图象与系数的关系,主要考查学生根据图形进行推理和辨析的能力,用了数形结合思想,题目比较好,但是难度偏大.
二.填空题(共1小题)
3.如图,在平面直角坐标系xOy中,矩形ABCO的顶点A,C分别在x轴,y轴的正半轴上,点D,E是CO的两个三等分点,过点D,E作x轴的平行线分别交AB于点F,G,反比例函数y=(x>0)的图象经过点G,分别交BC,DF于点Q,P,分别过点Q,P,作x轴的垂线,垂足分别为H,K.图中阴影部分的面积分别为S1,S2,S3.若OE=HK=1,则点G的坐标为 (6,1) ;若S1+S3=25,则S2= 5 .
【分析】若OE=HK=1,根据题意Q(,3),P(,2),G(k,1),进而求得Q(2,3),P(3,2),代入反比例函数y=(x>0)求得k的值,即可求得点G的坐标;
若S1+S3=25,由反比例函数系数k的几何意义可知,3S1=2S1+2S2=S1+S2+S3=k,即可得出S1=2S2,2S1=S2+S3,由S1+S3=25,得出S3=25﹣S1,经过变形得到6S2=S2+25,求得S2=5.
【解答】解:若OE=HK=1,
∵点D,E是CO的两个三等分点,
∴OC=3,PK=2,AG=1,
∴Q(,3),P(,2),G(k,1),
∴==,
∵HK=1,
∴OH=2,OK=3,
∴Q(2,3),P(3,2),
∵点Q,P,G在反比例函数y=(x>0)的图象上,
∴k=2×3=6,
∴G(6,1);
若S1+S3=25,
由反比例函数系数k的几何意义可知,3S1=2S1+2S2=S1+S2+S3=k,
∴S1=2S2,2S1=S2+S3,
∵S1+S3=25,
∴S3=25﹣S1,
∴2S1=S2+25﹣S1,
∴3S1=S2+25,
∴6S2=S2+25,
∴S2=5.
故答案为:(6,1),5.
【点评】本题考查了反比例函数系数k的几何意义,反比例函数图象上点的坐标特征,矩形的性质,熟知反比例函数系数k的几何意义是解题的关键.
三.解答题(共2小题)
4.某水库大坝的横截面是如图所示的四边形ABCD,其中AB∥CD,大坝顶上有一瞭望台PC,PC正前方有两艘渔船M,N.观察员在瞭望台顶端P处观测到渔船M的俯角α为31°,渔船N的俯角β为45°.已知MN所在直线与PC所在直线垂直,垂足为E,且PE长为30米.
(1)求两渔船M,N之间的距离(结果精确到1米);
(2)已知坝高24米,坝长100米,背水坡AD的坡度i=1:0.25,为提高大坝防洪能力,请施工队将大坝的背水坡通过填筑土石方进行加固,坝底BA加宽后变为BH,加固后背水坡DH的坡度i=1:1.75,施工队施工10天后,为尽快完成加固任务,施工队增加了机械设备,工作效率提高到原来的2倍,结果比原计划提前20天完成加固任务,施工队原计划平均每天填筑土石方多少立方米?
(参考数据:tan31°≈0.60,sin31°≈0.52)
【分析】(1)在直角△PEN,利用三角函数即可求得ME的长,根据MN=EM﹣EN求解;
(2)过点D作DN⊥AH于点N,利用三角函数求得AN和AH的长,进而求得△ADH的面积,得到需要填筑的土石方数,再根据结果比原计划提前20天完成,列方程求解.
【解答】解:(1)在直角△PEN中,∠PNE=45°,
∴EN=PE=30m,
在Rt△PME中,∠PME=31°,
∴ME==50(m),
则MN=EM﹣EN=20(m).
答:两渔船M、N之间的距离是20米;
(2)过点D作DQ⊥AH于点Q.
由题意得:tan∠DAB=4,tanH=,
在直角△DAQ中,AQ===6(m),
在直角△DHQ中,HQ===42(m).
故AH=HQ﹣AQ=42﹣6=36(m).
S△ADH=AH DQ=432(m2).
故需要填筑的土石方是V=SL=432×100=43200(m3).
设原计划平均每天填筑xm3,则原计划天完成,则增加机械设备后,现在平均每天填筑2xm3.
根据题意,得:10x+() 2x=43200,
解得:x=864.
经检验x=864是原方程的解.
答:施工队原计划平均每天填筑土石方864立方米.
【点评】本题考查了仰角的定义以及坡度,要求学生能借助仰角构造直角三角形并解直角三角形.
5.[证明体验](1)如图1,在△ABC和△BDE中,点A、B、D在同一直线上,∠A=∠CBE=∠D=90°,求证:△ABC∽△DEB.
(2)如图2,图3,AD=20,点B线段AD上的点,AC⊥AD,AC=4,连结BC,M为BC中点,将线段BM绕点B顺时针旋转90°至BE,连结DE.
[思考探究]①如图2,当DE=ME时,求AB的长.
[拓展延伸]②如图3,点G是CA延长线上一点,且AG=8,连结GE,∠G=∠D,求ED的长.
【分析】(1)利用同角的余角相等得∠C=∠DBE,可证明结论;
(2)①过点E作EF⊥AD,垂足为F,由(1)得△ABC∽△FEB,得,可得答案;
②过点M作AD的垂线交AD于点H,过点E作AD的垂线交AD于点F,过点D作DP⊥AD,过点E作NP⊥DP,交AC的延长线于N,首先利用AAS证明△MHB≌△BFE,得BF=MH=2,EF=BH,设EF=x,则DP=x,BH=AH=x,EP=FD=20﹣2﹣2x=18﹣2x,GN=x+8,AF=2x+2,再由∠GED=∠GAH=90°,由(1)得△NGE∽△PED,得,代入计算即可.
【解答】(1)证明:∵∠A=∠CBE=∠D=90°,
∴∠C+∠CBA=90°,∠CBA+∠DBE=90°,
∴∠C=∠DBE,
∴△ABC∽△DEB;
(2)解:①∵M绕点B顺时针旋转90°至E,M为BC的中点,
∴△BME为等腰直角三角形,,
∴BE=,
又∵DE=,
∴BE=DE,
如图,过点E作EF⊥AD,垂足为F,
则BF=DF,
∵∠A=∠CBE=∠BFE=90°,
由(1)得△ABC∽△FEB,
∴,
∵AC=4,
∴BF=2,
∴AB=AD﹣BF﹣FD=20﹣2﹣2=16;
②如图,过点M作AD的垂线交AD于点H,过点E作AD的垂线交AD于点F,过点D作DP⊥AD,过点E作NP⊥DP,交AC的延长线于N,
∵M为BC的中点,MH∥AC,
∴,
∴MH=,BH=AH,
∵∠MHB=∠MBE=∠BFE=90°,
由(1)得:∠HBM=∠FEB,
∵MB=EB,
∴△MHB≌△BFE(AAS),
∴BF=MH=2,EF=BH,
设EF=x,则DP=x,BH=AH=x,EP=FD=20﹣2﹣2x=18﹣2x,GN=x+8,AF=2x+2,
∵∠G=∠D,
∴∠GED=∠GAH=90°,
由(1)得△NGE∽△PED,
∴,
即,
解得x=6或x=﹣(舍去),
∴FD=18﹣2x=6,
∴ED==6.
【点评】本题是相似形综合题,主要考查了相似三角形的判定与性质,等腰直角三角形的性质,全等三角形的判定与性质,熟练掌握一线三等角基本模型是解题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
