浙江省中考数学考前冲刺每日一练12(精选全省各市历年经典真题,包含常考题型、易错题型、 小压轴、大压轴)
文档属性
| 名称 | 浙江省中考数学考前冲刺每日一练12(精选全省各市历年经典真题,包含常考题型、易错题型、 小压轴、大压轴) |
|
|
| 格式 | doc | ||
| 文件大小 | 366.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-24 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
浙江省中考数学考前冲刺每日一练12(精选全省各市历年经典真题,包含常考题型、易错题型、 小压轴、大压轴)
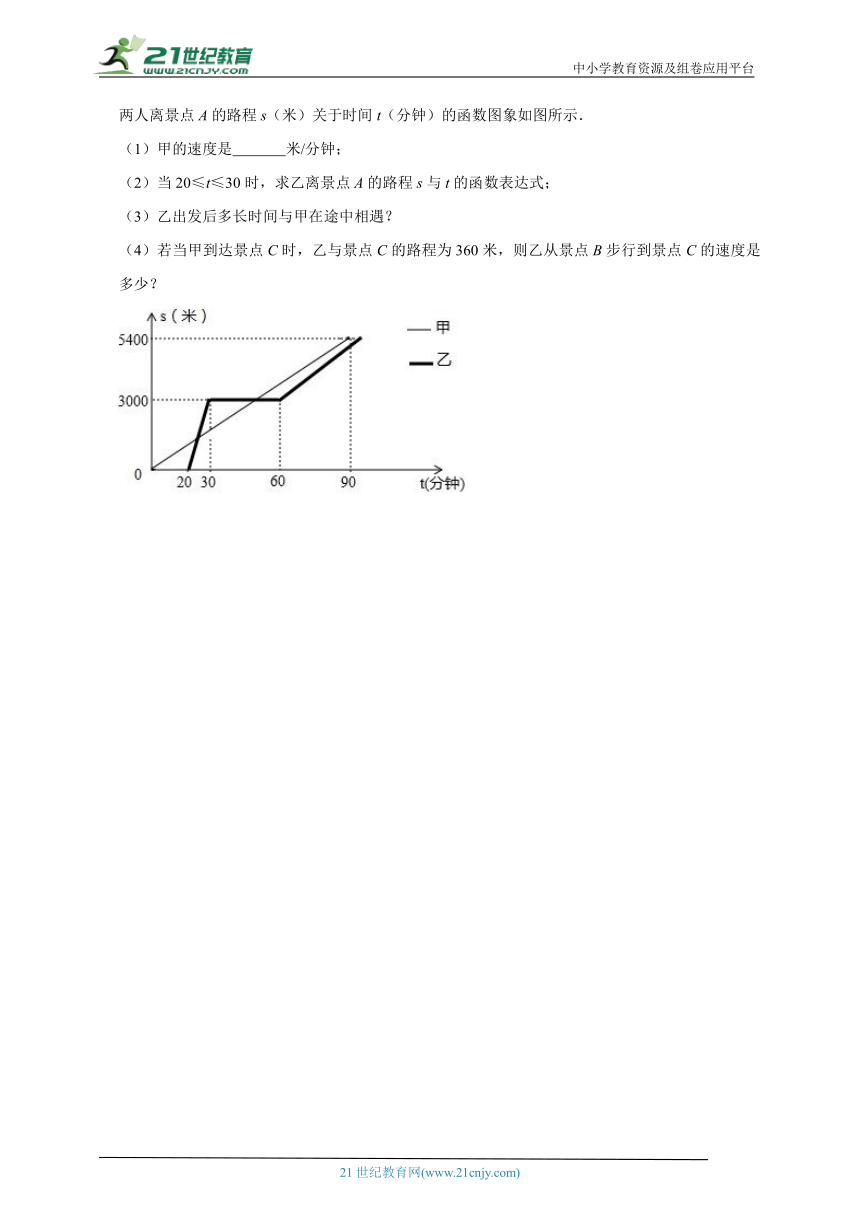
1.如图,抛物线y=ax2+bx+c过点(﹣1,0),(0,﹣1),顶点在第四象限,记P=2a﹣b,则P的取值范围是 .
2.如图,菱形ABCD的对角线AC、BD交于点O,且AC=6,BD=8.过O的直线EF交BC于E,交AD于F.把四边形CDFE沿着EF折叠得到四边形C'EFD',C'D'交AC于点G.当C'D'∥BD时,的值为 ,BE的长为 .
3.小明在手工制作课上,用面积为150πcm2,半径为15cm的扇形卡纸,围成一个圆锥侧面,则这个圆锥的底面半径为 cm.
4.如图,在6×5的方格纸中,线段AB的端点在格点上.
(1)在图1中,画一个以AB为边,面积为6的格点平行四边形ABCD(点C,D在点上);
(2)在图2中,画一个以AB为直角边,斜边为整数的格点直角△ABC(点C在格点上).
5.某景区在同一线路上顺次有三个景点A,B,C,甲、乙两名游客从景点A出发,甲步行到景点C;乙花20分钟时间排队后乘观光车先到景点B,在B处停留一段时间后,再步行到景点C.甲、乙两人离景点A的路程s(米)关于时间t(分钟)的函数图象如图所示.
(1)甲的速度是 米/分钟;
(2)当20≤t≤30时,求乙离景点A的路程s与t的函数表达式;
(3)乙出发后多长时间与甲在途中相遇?
(4)若当甲到达景点C时,乙与景点C的路程为360米,则乙从景点B步行到景点C的速度是多少?
浙江省中考数学考前冲刺每日一练12(精选全省各市历年经典真题,包含常考题型、易错题型、 小压轴、大压轴)参考答案与试题解析
一.选择题(共1小题)
1.如图,抛物线y=ax2+bx+c过点(﹣1,0),(0,﹣1),顶点在第四象限,记P=2a﹣b,则P的取值范围是( )
A.0<P<1 B.1<P<2 C.0<P<2 D.不能确定
【分析】由抛物线开口方向及对称轴的位置可判断a,b的符号,由抛物线经过(﹣1,0),(0,﹣1)可得a﹣b的值,进而求解.
【解答】解:∵抛物线开口向上,
∴a>0,
∵抛物线顶点在第四象限,
∴﹣>0,
∴b<0,
∵抛物线经过(﹣1,0),(0,﹣1),
∴a﹣b+c=0,c=﹣1,
∴a﹣b=1,
∴b=a﹣1,即﹣1<b<0,
∴2a﹣2b=2,
∵P=2a﹣2b+b,
∴1<P<2.
故选:B.
【点评】本题考查二次函数的性质,解题关键是掌握二次函数与方程的关系,掌握二次函数图象与系数的关系.
二.填空题(共2小题)
2.如图,菱形ABCD的对角线AC、BD交于点O,且AC=6,BD=8.过O的直线EF交BC于E,交AD于F.把四边形CDFE沿着EF折叠得到四边形C'EFD',C'D'交AC于点G.当C'D'∥BD时,的值为 ,BE的长为 .
【分析】连接OC′,OD′,根据轴对称的性质可得OC′=OC,OD′=OD,利用等面积法可得出OG的长,再根据勾股定理可分别求得C′G和D′G,进而可得出结论;连接DD,CC',过点D作DM⊥BD,则四边形GOMD'是矩形,勾股定理求得DD,CC',设BE=x,则EC=5﹣x,根据对称可知FD=BE=x,根据△FDD'∽△ECC′,由相似三角形的性质列出方程,即可求解.
【解答】解:如图,连接OC′,OD′,
在菱形ABCD中,AC=6,BD=8,
∴OA=OC=3,OB=OD=4,且AC⊥BD,
∴菱形的边长为5.
∵C′D′∥BD,
∴C′D′⊥AC,
由折叠可知,OC′=OC=3,OD′=OD=4,∠C′OD′=∠COD=90°,
∴OG==.
由勾股定理可知,C′G=,D′G=,
∴=;
如图,连接DD,CC',过点D作DM⊥BD,则四边形GOMD'是矩形,
∴DM=OG=,MG=OD=4,
∴DM=GM﹣DG=4﹣=,
∴D′D=.
∵C′G=,CG=OC+OG=3+=,
∴CC′=,
∴CC′:DD′=9:4.
设BE=x,则CE=C′E=10﹣x,
由菱形的对称性可知,DF=BE=x,且△CC′E∽△DD′F,
∴EC:DF=CC′:DD′=4:9,即(5﹣x):x=4:9,
解得x=.
故答案为:;.
【点评】本题属于四边形综合题,主要考查相似三角形的性质与判定,折叠的性质,勾股定理等相关知识,关键是掌握折叠的性质,作出辅助线由勾股定理求出CC′和DD′的长.
3.小明在手工制作课上,用面积为150πcm2,半径为15cm的扇形卡纸,围成一个圆锥侧面,则这个圆锥的底面半径为 10 cm.
【分析】先根据扇形的面积公式:S=l R(l为弧长,R为扇形的半径)计算出扇形的弧长,然后根据圆锥的侧面展开图为扇形,扇形的弧长等于圆锥的底面圆的周长,利用圆的周长公式计算出圆锥的底面半径.
【解答】解:∵S=l R,
∴ l 15=150π,解得l=20π,
设圆锥的底面半径为rcm,
∴2π r=20π,
∴r=10(cm).
故答案为:10.
【点评】本题考查了圆锥的计算:圆锥的侧面展开图为扇形,扇形的弧长等于圆锥的底面圆的周长,扇形的半径等于圆锥的母线长;也考查了扇形的面积公式:S=l R(l为弧长,R为扇形的半径).
三.解答题(共2小题)
4.如图,在6×5的方格纸中,线段AB的端点在格点上.
(1)在图1中,画一个以AB为边,面积为6的格点平行四边形ABCD(点C,D在点上);
(2)在图2中,画一个以AB为直角边,斜边为整数的格点直角△ABC(点C在格点上).
【分析】(1)画一个底为3,高为2的平行四边形即可;
(2)画一个斜边为5的直角三角形即可.
【解答】解:(1)如图1中,四边形ABCD即为所求;
(2)如图2中,△ABC即为所求.
【点评】本题考查作图﹣应用与设计作图,解题的关键是理解题意,学会利用数形结合的思想解决问题.
5.某景区在同一线路上顺次有三个景点A,B,C,甲、乙两名游客从景点A出发,甲步行到景点C;乙花20分钟时间排队后乘观光车先到景点B,在B处停留一段时间后,再步行到景点C.甲、乙两人离景点A的路程s(米)关于时间t(分钟)的函数图象如图所示.
(1)甲的速度是 60 米/分钟;
(2)当20≤t≤30时,求乙离景点A的路程s与t的函数表达式;
(3)乙出发后多长时间与甲在途中相遇?
(4)若当甲到达景点C时,乙与景点C的路程为360米,则乙从景点B步行到景点C的速度是多少?
【分析】(1)由图象可得甲行走的路程和时间,即可求甲的速度;
(2)由待定系数法可求乙离景点A的路程s与t的函数表达式;
(3)两人相遇实际上是函数图象求交点;
(4)由乙从B景点开始行走的路程+360=景点B和景点C之间的距离,可列方程解即可.
【解答】解:(1)甲的速度==60米/分钟,
故答案为:60
(2)当20≤t≤30时,设s=mt+n,
由题意得
解得
∴s=300t﹣6000
(3)当20≤t≤30时,60t=300t﹣6000,
解得t=25,
∴乙出发后时间=25﹣20=5,
当30≤t≤60时,60t=3000,
解得t=50,
∴乙出发后时间=50﹣20=30,
综上所述:乙出发5分钟和30分钟时与甲在途中相遇;
(4)设乙从B步行到C的速度是x米/分钟,
由题意得5400﹣3000﹣(90﹣60)x=360,
解得x=68,
所以乙从景点B步行到景点C的速度是68米/分钟.
【点评】本题是一次函数实际应用问题,考查了对一次函数图象代表意义的分析和从方程角度解决一次函数问题.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
浙江省中考数学考前冲刺每日一练12(精选全省各市历年经典真题,包含常考题型、易错题型、 小压轴、大压轴)
1.如图,抛物线y=ax2+bx+c过点(﹣1,0),(0,﹣1),顶点在第四象限,记P=2a﹣b,则P的取值范围是 .
2.如图,菱形ABCD的对角线AC、BD交于点O,且AC=6,BD=8.过O的直线EF交BC于E,交AD于F.把四边形CDFE沿着EF折叠得到四边形C'EFD',C'D'交AC于点G.当C'D'∥BD时,的值为 ,BE的长为 .
3.小明在手工制作课上,用面积为150πcm2,半径为15cm的扇形卡纸,围成一个圆锥侧面,则这个圆锥的底面半径为 cm.
4.如图,在6×5的方格纸中,线段AB的端点在格点上.
(1)在图1中,画一个以AB为边,面积为6的格点平行四边形ABCD(点C,D在点上);
(2)在图2中,画一个以AB为直角边,斜边为整数的格点直角△ABC(点C在格点上).
5.某景区在同一线路上顺次有三个景点A,B,C,甲、乙两名游客从景点A出发,甲步行到景点C;乙花20分钟时间排队后乘观光车先到景点B,在B处停留一段时间后,再步行到景点C.甲、乙两人离景点A的路程s(米)关于时间t(分钟)的函数图象如图所示.
(1)甲的速度是 米/分钟;
(2)当20≤t≤30时,求乙离景点A的路程s与t的函数表达式;
(3)乙出发后多长时间与甲在途中相遇?
(4)若当甲到达景点C时,乙与景点C的路程为360米,则乙从景点B步行到景点C的速度是多少?
浙江省中考数学考前冲刺每日一练12(精选全省各市历年经典真题,包含常考题型、易错题型、 小压轴、大压轴)参考答案与试题解析
一.选择题(共1小题)
1.如图,抛物线y=ax2+bx+c过点(﹣1,0),(0,﹣1),顶点在第四象限,记P=2a﹣b,则P的取值范围是( )
A.0<P<1 B.1<P<2 C.0<P<2 D.不能确定
【分析】由抛物线开口方向及对称轴的位置可判断a,b的符号,由抛物线经过(﹣1,0),(0,﹣1)可得a﹣b的值,进而求解.
【解答】解:∵抛物线开口向上,
∴a>0,
∵抛物线顶点在第四象限,
∴﹣>0,
∴b<0,
∵抛物线经过(﹣1,0),(0,﹣1),
∴a﹣b+c=0,c=﹣1,
∴a﹣b=1,
∴b=a﹣1,即﹣1<b<0,
∴2a﹣2b=2,
∵P=2a﹣2b+b,
∴1<P<2.
故选:B.
【点评】本题考查二次函数的性质,解题关键是掌握二次函数与方程的关系,掌握二次函数图象与系数的关系.
二.填空题(共2小题)
2.如图,菱形ABCD的对角线AC、BD交于点O,且AC=6,BD=8.过O的直线EF交BC于E,交AD于F.把四边形CDFE沿着EF折叠得到四边形C'EFD',C'D'交AC于点G.当C'D'∥BD时,的值为 ,BE的长为 .
【分析】连接OC′,OD′,根据轴对称的性质可得OC′=OC,OD′=OD,利用等面积法可得出OG的长,再根据勾股定理可分别求得C′G和D′G,进而可得出结论;连接DD,CC',过点D作DM⊥BD,则四边形GOMD'是矩形,勾股定理求得DD,CC',设BE=x,则EC=5﹣x,根据对称可知FD=BE=x,根据△FDD'∽△ECC′,由相似三角形的性质列出方程,即可求解.
【解答】解:如图,连接OC′,OD′,
在菱形ABCD中,AC=6,BD=8,
∴OA=OC=3,OB=OD=4,且AC⊥BD,
∴菱形的边长为5.
∵C′D′∥BD,
∴C′D′⊥AC,
由折叠可知,OC′=OC=3,OD′=OD=4,∠C′OD′=∠COD=90°,
∴OG==.
由勾股定理可知,C′G=,D′G=,
∴=;
如图,连接DD,CC',过点D作DM⊥BD,则四边形GOMD'是矩形,
∴DM=OG=,MG=OD=4,
∴DM=GM﹣DG=4﹣=,
∴D′D=.
∵C′G=,CG=OC+OG=3+=,
∴CC′=,
∴CC′:DD′=9:4.
设BE=x,则CE=C′E=10﹣x,
由菱形的对称性可知,DF=BE=x,且△CC′E∽△DD′F,
∴EC:DF=CC′:DD′=4:9,即(5﹣x):x=4:9,
解得x=.
故答案为:;.
【点评】本题属于四边形综合题,主要考查相似三角形的性质与判定,折叠的性质,勾股定理等相关知识,关键是掌握折叠的性质,作出辅助线由勾股定理求出CC′和DD′的长.
3.小明在手工制作课上,用面积为150πcm2,半径为15cm的扇形卡纸,围成一个圆锥侧面,则这个圆锥的底面半径为 10 cm.
【分析】先根据扇形的面积公式:S=l R(l为弧长,R为扇形的半径)计算出扇形的弧长,然后根据圆锥的侧面展开图为扇形,扇形的弧长等于圆锥的底面圆的周长,利用圆的周长公式计算出圆锥的底面半径.
【解答】解:∵S=l R,
∴ l 15=150π,解得l=20π,
设圆锥的底面半径为rcm,
∴2π r=20π,
∴r=10(cm).
故答案为:10.
【点评】本题考查了圆锥的计算:圆锥的侧面展开图为扇形,扇形的弧长等于圆锥的底面圆的周长,扇形的半径等于圆锥的母线长;也考查了扇形的面积公式:S=l R(l为弧长,R为扇形的半径).
三.解答题(共2小题)
4.如图,在6×5的方格纸中,线段AB的端点在格点上.
(1)在图1中,画一个以AB为边,面积为6的格点平行四边形ABCD(点C,D在点上);
(2)在图2中,画一个以AB为直角边,斜边为整数的格点直角△ABC(点C在格点上).
【分析】(1)画一个底为3,高为2的平行四边形即可;
(2)画一个斜边为5的直角三角形即可.
【解答】解:(1)如图1中,四边形ABCD即为所求;
(2)如图2中,△ABC即为所求.
【点评】本题考查作图﹣应用与设计作图,解题的关键是理解题意,学会利用数形结合的思想解决问题.
5.某景区在同一线路上顺次有三个景点A,B,C,甲、乙两名游客从景点A出发,甲步行到景点C;乙花20分钟时间排队后乘观光车先到景点B,在B处停留一段时间后,再步行到景点C.甲、乙两人离景点A的路程s(米)关于时间t(分钟)的函数图象如图所示.
(1)甲的速度是 60 米/分钟;
(2)当20≤t≤30时,求乙离景点A的路程s与t的函数表达式;
(3)乙出发后多长时间与甲在途中相遇?
(4)若当甲到达景点C时,乙与景点C的路程为360米,则乙从景点B步行到景点C的速度是多少?
【分析】(1)由图象可得甲行走的路程和时间,即可求甲的速度;
(2)由待定系数法可求乙离景点A的路程s与t的函数表达式;
(3)两人相遇实际上是函数图象求交点;
(4)由乙从B景点开始行走的路程+360=景点B和景点C之间的距离,可列方程解即可.
【解答】解:(1)甲的速度==60米/分钟,
故答案为:60
(2)当20≤t≤30时,设s=mt+n,
由题意得
解得
∴s=300t﹣6000
(3)当20≤t≤30时,60t=300t﹣6000,
解得t=25,
∴乙出发后时间=25﹣20=5,
当30≤t≤60时,60t=3000,
解得t=50,
∴乙出发后时间=50﹣20=30,
综上所述:乙出发5分钟和30分钟时与甲在途中相遇;
(4)设乙从B步行到C的速度是x米/分钟,
由题意得5400﹣3000﹣(90﹣60)x=360,
解得x=68,
所以乙从景点B步行到景点C的速度是68米/分钟.
【点评】本题是一次函数实际应用问题,考查了对一次函数图象代表意义的分析和从方程角度解决一次函数问题.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
