浙江省中考数学考前冲刺每日一练8(精选全省各市历年经典真题,包含常考题型、易错题型、 小压轴、大压轴)
文档属性
| 名称 | 浙江省中考数学考前冲刺每日一练8(精选全省各市历年经典真题,包含常考题型、易错题型、 小压轴、大压轴) |  | |
| 格式 | doc | ||
| 文件大小 | 469.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-24 09:27:45 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
浙江省中考数学考前冲刺每日一练8(精选全省各市历年经典真题,包含常考题型、易错题型、 小压轴、大压轴)
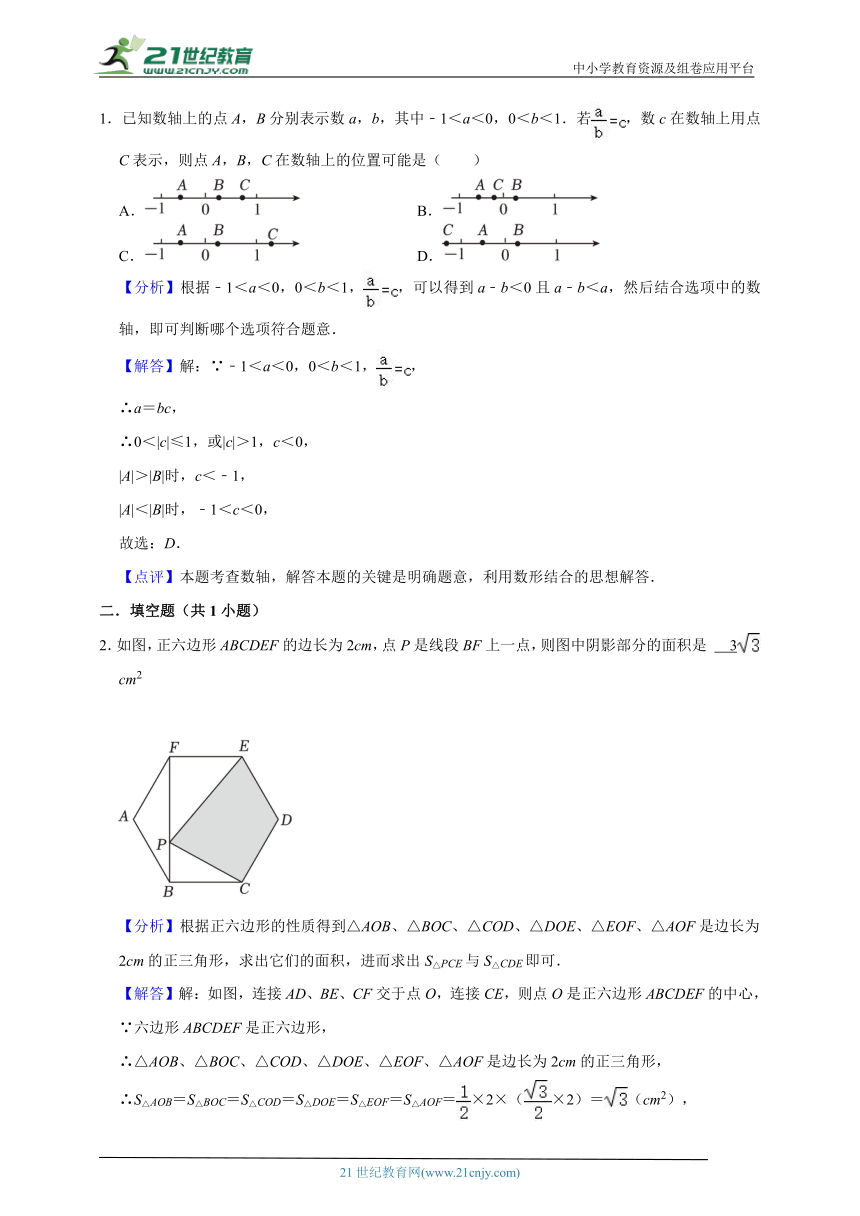
1.已知数轴上的点A,B分别表示数a,b,其中﹣1<a<0,0<b<1.若,数c在数轴上用点C表示,则点A,B,C在数轴上的位置可能是( )
A. B.
C. D.
2.如图,正六边形ABCDEF的边长为2cm,点P是线段BF上一点,则图中阴影部分的面积是 cm2
3.好事成双,再上一个网格题:
如图,在8×8的方格纸中,△ABC的三个顶点都在格点上.
(1)在图1中找出所有合适的格点D,使得∠BDC=∠BAC.
(2)在图2中找出所有合适的格点E,使得∠CEB=2∠CAB.
4.设二次函数y=ax2+bx+c(a>0,b,c是实数),其图象上有两点(1,m),(3,n),且图象的对称轴为直线x=t.
(1)当c=2,m=n时,求二次函数图象与y轴交点的坐标及t的值.
(2)点(x0,m)(x0≠1)在函数图象上,若m<n<c,求t的取值范围及x0的取值范围.
5.根据背景素材,探索解决问题.
测算石拱桥拱圈的半径
素材1 某数学兴趣小组测算一座石拱桥拱圈的半径(如图1),石拱桥由侧面为矩形的花岗岩叠砌而成,上、下的花岗岩错缝连接(花岗岩的各个顶点落在上、下花岗岩相应边的中点,如图2).
素材2 通过观察发现A,B,C三个点都在拱圈上,A是拱圈的最高点,且在两块花岗岩的连接处(不在花岗岩的顶点处),B,C两个点都是花岗岩的顶点(如图3).
素材3 如果没有带测量工具,可以用身体上的“尺子”来测,比如前臂长(包括手掌、手指)称为1肘(如图4),利用该方法测得一块花岗岩的长和高(如图5).
解决问题
任务1 获取数据 通过观察计算,得到B,C两点之间的水平距离为 肘,铅垂距离(高度差)为 肘.
任务2 分析计算 通过观察、计算,得到石拱桥拱圈的半径为 肘.
任务3 预测判断 若水平面位于点C处,一艘宽6肘,水面之上的高为7肘的货船是否能顺利通过此石拱桥?请说明理由.
注:在测量、计算时,都以“肘”为单位.
浙江省中考数学考前冲刺每日一练8(精选全省各市历年经典真题,包含常考题型、易错题型、 小压轴、大压轴)参考答案与试题解析
一.选择题(共1小题)
1.已知数轴上的点A,B分别表示数a,b,其中﹣1<a<0,0<b<1.若,数c在数轴上用点C表示,则点A,B,C在数轴上的位置可能是( )
A. B.
C. D.
【分析】根据﹣1<a<0,0<b<1,,可以得到a﹣b<0且a﹣b<a,然后结合选项中的数轴,即可判断哪个选项符合题意.
【解答】解:∵﹣1<a<0,0<b<1,,
∴a=bc,
∴0<|c|≤1,或|c|>1,c<0,
|A|>|B|时,c<﹣1,
|A|<|B|时,﹣1<c<0,
故选:D.
【点评】本题考查数轴,解答本题的关键是明确题意,利用数形结合的思想解答.
二.填空题(共1小题)
2.如图,正六边形ABCDEF的边长为2cm,点P是线段BF上一点,则图中阴影部分的面积是 3 cm2
【分析】根据正六边形的性质得到△AOB、△BOC、△COD、△DOE、△EOF、△AOF是边长为2cm的正三角形,求出它们的面积,进而求出S△PCE与S△CDE即可.
【解答】解:如图,连接AD、BE、CF交于点O,连接CE,则点O是正六边形ABCDEF的中心,
∵六边形ABCDEF是正六边形,
∴△AOB、△BOC、△COD、△DOE、△EOF、△AOF是边长为2cm的正三角形,
∴S△AOB=S△BOC=S△COD=S△DOE=S△EOF=S△AOF=×2×(×2)=(cm2),
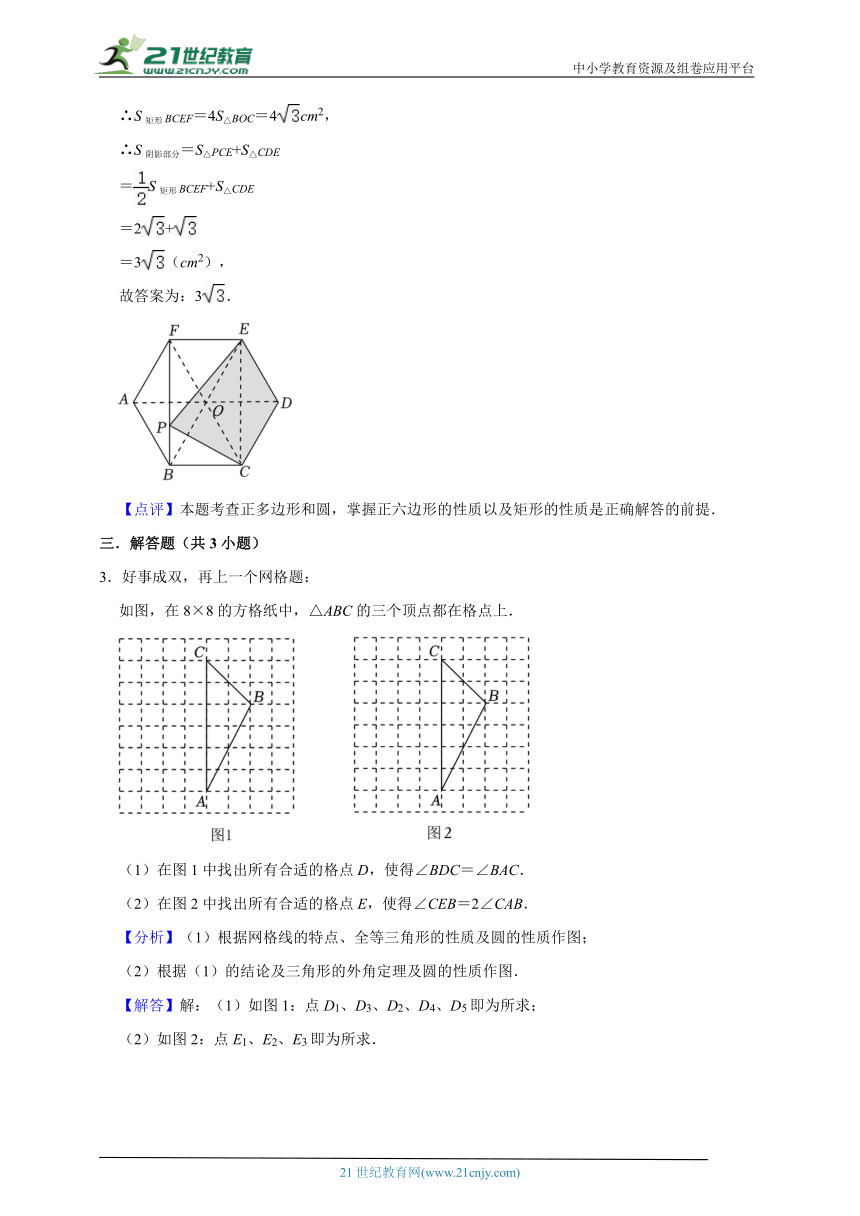
∴S矩形BCEF=4S△BOC=4cm2,
∴S阴影部分=S△PCE+S△CDE
=S矩形BCEF+S△CDE
=2+
=3(cm2),
故答案为:3.
【点评】本题考查正多边形和圆,掌握正六边形的性质以及矩形的性质是正确解答的前提.
三.解答题(共3小题)
3.好事成双,再上一个网格题:
如图,在8×8的方格纸中,△ABC的三个顶点都在格点上.
(1)在图1中找出所有合适的格点D,使得∠BDC=∠BAC.
(2)在图2中找出所有合适的格点E,使得∠CEB=2∠CAB.
【分析】(1)根据网格线的特点、全等三角形的性质及圆的性质作图;
(2)根据(1)的结论及三角形的外角定理及圆的性质作图.
【解答】解:(1)如图1:点D1、D3、D2、D4、D5即为所求;
(2)如图2:点E1、E2、E3即为所求.
【点评】本题考查了作图的应用和设计,掌握网格线的特点、三角形全等的性质及外角定理是解题的关键.
4.设二次函数y=ax2+bx+c(a>0,b,c是实数),其图象上有两点(1,m),(3,n),且图象的对称轴为直线x=t.
(1)当c=2,m=n时,求二次函数图象与y轴交点的坐标及t的值.
(2)点(x0,m)(x0≠1)在函数图象上,若m<n<c,求t的取值范围及x0的取值范围.
【分析】(1)由c=2可得抛物线与y轴的交点坐标,由m=n可得点(1,m),(3,n)关于抛物线对称轴对称,从而可得答案;
(2)再根据m<n<c,可确定出3a<﹣b<4a,结合2a>0,可得对称轴的取值范围,再利用对称轴可表示为直线x=,进而可确定x0的取值范围.
【解答】解:(1)∵c=2,
∴抛物线为:y=ax2+bx+2(a>0),
∴当x=0,则y=2,
∴抛物线与y轴的交点坐标为:(0,2),
∵m=n,
∴点(1,m),(3,n)关于抛物线的对称轴对称,
∴抛物线的对称轴为直线x=t==2.
(2)∵m<n<c,
∴a+b+c<9a+3b+c<c,
解得﹣4a<b<﹣3a,
∴3a<﹣b<4a,而2a>0,
∴,即<t<2,
∵点(1,m),(x0,m)(x0≠﹣1)在抛物线上,
∴抛物线的对称轴为直线x=,
∴<<2,
解得:2<x0<3,
∴x0的取值范围2<x0<3.
【点评】本题考查二次函数的性质,二次函数图象上点的坐标特征,掌握关于抛物线对称轴对称的两个点的坐标关系是解题关键.
5.根据背景素材,探索解决问题.
测算石拱桥拱圈的半径
素材1 某数学兴趣小组测算一座石拱桥拱圈的半径(如图1),石拱桥由侧面为矩形的花岗岩叠砌而成,上、下的花岗岩错缝连接(花岗岩的各个顶点落在上、下花岗岩相应边的中点,如图2).
素材2 通过观察发现A,B,C三个点都在拱圈上,A是拱圈的最高点,且在两块花岗岩的连接处(不在花岗岩的顶点处),B,C两个点都是花岗岩的顶点(如图3).
素材3 如果没有带测量工具,可以用身体上的“尺子”来测,比如前臂长(包括手掌、手指)称为1肘(如图4),利用该方法测得一块花岗岩的长和高(如图5).
解决问题
任务1 获取数据 通过观察计算,得到B,C两点之间的水平距离为 5 肘,铅垂距离(高度差)为 5 肘.
任务2 分析计算 通过观察、计算,得到石拱桥拱圈的半径为 肘.
任务3 预测判断 若水平面位于点C处,一艘宽6肘,水面之上的高为7肘的货船是否能顺利通过此石拱桥?请说明理由.
注:在测量、计算时,都以“肘”为单位.
【分析】任务1:根据素材3,观察图形可知一块花岗岩的长为2肘、宽为1肘,根据素材1、素材2,观察图形,得出B,C两点之间的水平距离及铅垂距离(高度差)即可;
任务2:作过点C的水平线,过点A作该水平线的垂线,垂足为E,作BD⊥AE于点D,记圆心为O,连结CO,BO.观察图形,得出CE,DB,DE的长,设OE=a,则DO=DE+OE=5+a,根据勾股定理,OB2=DB2+OD2,OC2=OE2+EC2,半径OB=OC,得到方程 (5+a)2+82=a2+132,求解方程得出a=8,计算 ,即可得出石拱桥拱圈的半径;
任务3:根据垂径定理可知BD=3肘,利用勾股定理求出OD,DE的长,即可判断答案.
【解答】解 任务1:根据素材3,观察图形可知一块花岗岩的长 为2肘、宽为1肘,
根据素材1、素材2,观察图形,B,C两点之间的水 平距离有2.5块花岗岩的长,
则2.5×2=5(肘),
B,C两点之间的铅垂距离(高度差)有5块花岗岩 的宽,
则5×1=5(肘),
故答案为:5,5.
任务2:如图,作过点C的水平线,过点A作该水平 线的垂线,垂足为E,作BD⊥AE于点D,记圆心为O,连结CO,BO,
∵A是拱圈的最高点,
∴圆心O在AE的延长线上,
观察图形,CE=6.5×2=13(肘),DB=8 (肘),DE=5(肘),
设OE=a,
则DO=DE+OE=5+a,
∵OB2=DB2+OD2,OC2=OE2+EC2 OB=OC,
∴(5+a)2+82=a2+132,
解得:a=8,
∴,
∴石拱桥拱圈的半径为 时,
故答案为:.
任务3:货船不能通过此石拱桥.理由如下:
由垂径定理得,BD=3 (肘),
∴ (肘),
∴ (肘),
∵,
∴,
即DE<7(肘),
所以货船不能通过此石拱桥.
【点评】本题主要考查了垂径定理的应用,勾股定理的应用,熟练掌握知识点、观察图形、作辅助线计算是解题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
浙江省中考数学考前冲刺每日一练8(精选全省各市历年经典真题,包含常考题型、易错题型、 小压轴、大压轴)
1.已知数轴上的点A,B分别表示数a,b,其中﹣1<a<0,0<b<1.若,数c在数轴上用点C表示,则点A,B,C在数轴上的位置可能是( )
A. B.
C. D.
2.如图,正六边形ABCDEF的边长为2cm,点P是线段BF上一点,则图中阴影部分的面积是 cm2
3.好事成双,再上一个网格题:
如图,在8×8的方格纸中,△ABC的三个顶点都在格点上.
(1)在图1中找出所有合适的格点D,使得∠BDC=∠BAC.
(2)在图2中找出所有合适的格点E,使得∠CEB=2∠CAB.
4.设二次函数y=ax2+bx+c(a>0,b,c是实数),其图象上有两点(1,m),(3,n),且图象的对称轴为直线x=t.
(1)当c=2,m=n时,求二次函数图象与y轴交点的坐标及t的值.
(2)点(x0,m)(x0≠1)在函数图象上,若m<n<c,求t的取值范围及x0的取值范围.
5.根据背景素材,探索解决问题.
测算石拱桥拱圈的半径
素材1 某数学兴趣小组测算一座石拱桥拱圈的半径(如图1),石拱桥由侧面为矩形的花岗岩叠砌而成,上、下的花岗岩错缝连接(花岗岩的各个顶点落在上、下花岗岩相应边的中点,如图2).
素材2 通过观察发现A,B,C三个点都在拱圈上,A是拱圈的最高点,且在两块花岗岩的连接处(不在花岗岩的顶点处),B,C两个点都是花岗岩的顶点(如图3).
素材3 如果没有带测量工具,可以用身体上的“尺子”来测,比如前臂长(包括手掌、手指)称为1肘(如图4),利用该方法测得一块花岗岩的长和高(如图5).
解决问题
任务1 获取数据 通过观察计算,得到B,C两点之间的水平距离为 肘,铅垂距离(高度差)为 肘.
任务2 分析计算 通过观察、计算,得到石拱桥拱圈的半径为 肘.
任务3 预测判断 若水平面位于点C处,一艘宽6肘,水面之上的高为7肘的货船是否能顺利通过此石拱桥?请说明理由.
注:在测量、计算时,都以“肘”为单位.
浙江省中考数学考前冲刺每日一练8(精选全省各市历年经典真题,包含常考题型、易错题型、 小压轴、大压轴)参考答案与试题解析
一.选择题(共1小题)
1.已知数轴上的点A,B分别表示数a,b,其中﹣1<a<0,0<b<1.若,数c在数轴上用点C表示,则点A,B,C在数轴上的位置可能是( )
A. B.
C. D.
【分析】根据﹣1<a<0,0<b<1,,可以得到a﹣b<0且a﹣b<a,然后结合选项中的数轴,即可判断哪个选项符合题意.
【解答】解:∵﹣1<a<0,0<b<1,,
∴a=bc,
∴0<|c|≤1,或|c|>1,c<0,
|A|>|B|时,c<﹣1,
|A|<|B|时,﹣1<c<0,
故选:D.
【点评】本题考查数轴,解答本题的关键是明确题意,利用数形结合的思想解答.
二.填空题(共1小题)
2.如图,正六边形ABCDEF的边长为2cm,点P是线段BF上一点,则图中阴影部分的面积是 3 cm2
【分析】根据正六边形的性质得到△AOB、△BOC、△COD、△DOE、△EOF、△AOF是边长为2cm的正三角形,求出它们的面积,进而求出S△PCE与S△CDE即可.
【解答】解:如图,连接AD、BE、CF交于点O,连接CE,则点O是正六边形ABCDEF的中心,
∵六边形ABCDEF是正六边形,
∴△AOB、△BOC、△COD、△DOE、△EOF、△AOF是边长为2cm的正三角形,
∴S△AOB=S△BOC=S△COD=S△DOE=S△EOF=S△AOF=×2×(×2)=(cm2),
∴S矩形BCEF=4S△BOC=4cm2,
∴S阴影部分=S△PCE+S△CDE
=S矩形BCEF+S△CDE
=2+
=3(cm2),
故答案为:3.
【点评】本题考查正多边形和圆,掌握正六边形的性质以及矩形的性质是正确解答的前提.
三.解答题(共3小题)
3.好事成双,再上一个网格题:
如图,在8×8的方格纸中,△ABC的三个顶点都在格点上.
(1)在图1中找出所有合适的格点D,使得∠BDC=∠BAC.
(2)在图2中找出所有合适的格点E,使得∠CEB=2∠CAB.
【分析】(1)根据网格线的特点、全等三角形的性质及圆的性质作图;
(2)根据(1)的结论及三角形的外角定理及圆的性质作图.
【解答】解:(1)如图1:点D1、D3、D2、D4、D5即为所求;
(2)如图2:点E1、E2、E3即为所求.
【点评】本题考查了作图的应用和设计,掌握网格线的特点、三角形全等的性质及外角定理是解题的关键.
4.设二次函数y=ax2+bx+c(a>0,b,c是实数),其图象上有两点(1,m),(3,n),且图象的对称轴为直线x=t.
(1)当c=2,m=n时,求二次函数图象与y轴交点的坐标及t的值.
(2)点(x0,m)(x0≠1)在函数图象上,若m<n<c,求t的取值范围及x0的取值范围.
【分析】(1)由c=2可得抛物线与y轴的交点坐标,由m=n可得点(1,m),(3,n)关于抛物线对称轴对称,从而可得答案;
(2)再根据m<n<c,可确定出3a<﹣b<4a,结合2a>0,可得对称轴的取值范围,再利用对称轴可表示为直线x=,进而可确定x0的取值范围.
【解答】解:(1)∵c=2,
∴抛物线为:y=ax2+bx+2(a>0),
∴当x=0,则y=2,
∴抛物线与y轴的交点坐标为:(0,2),
∵m=n,
∴点(1,m),(3,n)关于抛物线的对称轴对称,
∴抛物线的对称轴为直线x=t==2.
(2)∵m<n<c,
∴a+b+c<9a+3b+c<c,
解得﹣4a<b<﹣3a,
∴3a<﹣b<4a,而2a>0,
∴,即<t<2,
∵点(1,m),(x0,m)(x0≠﹣1)在抛物线上,
∴抛物线的对称轴为直线x=,
∴<<2,
解得:2<x0<3,
∴x0的取值范围2<x0<3.
【点评】本题考查二次函数的性质,二次函数图象上点的坐标特征,掌握关于抛物线对称轴对称的两个点的坐标关系是解题关键.
5.根据背景素材,探索解决问题.
测算石拱桥拱圈的半径
素材1 某数学兴趣小组测算一座石拱桥拱圈的半径(如图1),石拱桥由侧面为矩形的花岗岩叠砌而成,上、下的花岗岩错缝连接(花岗岩的各个顶点落在上、下花岗岩相应边的中点,如图2).
素材2 通过观察发现A,B,C三个点都在拱圈上,A是拱圈的最高点,且在两块花岗岩的连接处(不在花岗岩的顶点处),B,C两个点都是花岗岩的顶点(如图3).
素材3 如果没有带测量工具,可以用身体上的“尺子”来测,比如前臂长(包括手掌、手指)称为1肘(如图4),利用该方法测得一块花岗岩的长和高(如图5).
解决问题
任务1 获取数据 通过观察计算,得到B,C两点之间的水平距离为 5 肘,铅垂距离(高度差)为 5 肘.
任务2 分析计算 通过观察、计算,得到石拱桥拱圈的半径为 肘.
任务3 预测判断 若水平面位于点C处,一艘宽6肘,水面之上的高为7肘的货船是否能顺利通过此石拱桥?请说明理由.
注:在测量、计算时,都以“肘”为单位.
【分析】任务1:根据素材3,观察图形可知一块花岗岩的长为2肘、宽为1肘,根据素材1、素材2,观察图形,得出B,C两点之间的水平距离及铅垂距离(高度差)即可;
任务2:作过点C的水平线,过点A作该水平线的垂线,垂足为E,作BD⊥AE于点D,记圆心为O,连结CO,BO.观察图形,得出CE,DB,DE的长,设OE=a,则DO=DE+OE=5+a,根据勾股定理,OB2=DB2+OD2,OC2=OE2+EC2,半径OB=OC,得到方程 (5+a)2+82=a2+132,求解方程得出a=8,计算 ,即可得出石拱桥拱圈的半径;
任务3:根据垂径定理可知BD=3肘,利用勾股定理求出OD,DE的长,即可判断答案.
【解答】解 任务1:根据素材3,观察图形可知一块花岗岩的长 为2肘、宽为1肘,
根据素材1、素材2,观察图形,B,C两点之间的水 平距离有2.5块花岗岩的长,
则2.5×2=5(肘),
B,C两点之间的铅垂距离(高度差)有5块花岗岩 的宽,
则5×1=5(肘),
故答案为:5,5.
任务2:如图,作过点C的水平线,过点A作该水平 线的垂线,垂足为E,作BD⊥AE于点D,记圆心为O,连结CO,BO,
∵A是拱圈的最高点,
∴圆心O在AE的延长线上,
观察图形,CE=6.5×2=13(肘),DB=8 (肘),DE=5(肘),
设OE=a,
则DO=DE+OE=5+a,
∵OB2=DB2+OD2,OC2=OE2+EC2 OB=OC,
∴(5+a)2+82=a2+132,
解得:a=8,
∴,
∴石拱桥拱圈的半径为 时,
故答案为:.
任务3:货船不能通过此石拱桥.理由如下:
由垂径定理得,BD=3 (肘),
∴ (肘),
∴ (肘),
∵,
∴,
即DE<7(肘),
所以货船不能通过此石拱桥.
【点评】本题主要考查了垂径定理的应用,勾股定理的应用,熟练掌握知识点、观察图形、作辅助线计算是解题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
