浙江省中考数学考前冲刺每日一练18(精选全省各市历年经典真题,包含常考题型、易错题型、 小压轴、大压轴)
文档属性
| 名称 | 浙江省中考数学考前冲刺每日一练18(精选全省各市历年经典真题,包含常考题型、易错题型、 小压轴、大压轴) |

|
|
| 格式 | doc | ||
| 文件大小 | 343.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-24 00:00:00 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
浙江省中考数学考前冲刺每日一练18(精选全省各市历年经典真题,包含常考题型、易错题型、 小压轴、大压轴)
1.下列说法正确的个数是( )
①一组数据的众数只有一个;②样本的方差越小,波动性越小,说明样本稳定性越好;③一组数据的中位数一定是这组数据中的某一数据;④一组数据的众数一定比平均数大;⑤一组数据的方差一定是正数.
A.0个 B.1个 C.2个 D.4个
2.若式子在实数范围内有意义,则x的取值范围是( )
A.x>﹣1 B.x≥﹣1且x≠0 C.x>﹣1且x≠0 D.x≠0
3.如图,二次函数y1=ax2+bx+c的图象与反比例函数y2=的图象交于,B(1,1),C(﹣1,﹣1)三点.对于实数a,b,我们定义符号max{a,b}的意义为:当a≥b时,max{a,b}=a;当a<b时,max{a,b}=b;如max{4,﹣2}=4,max{3,3}=3.若函数y=,则函数y的最小值是( )
A.3 B.1 C.﹣1 D.﹣2
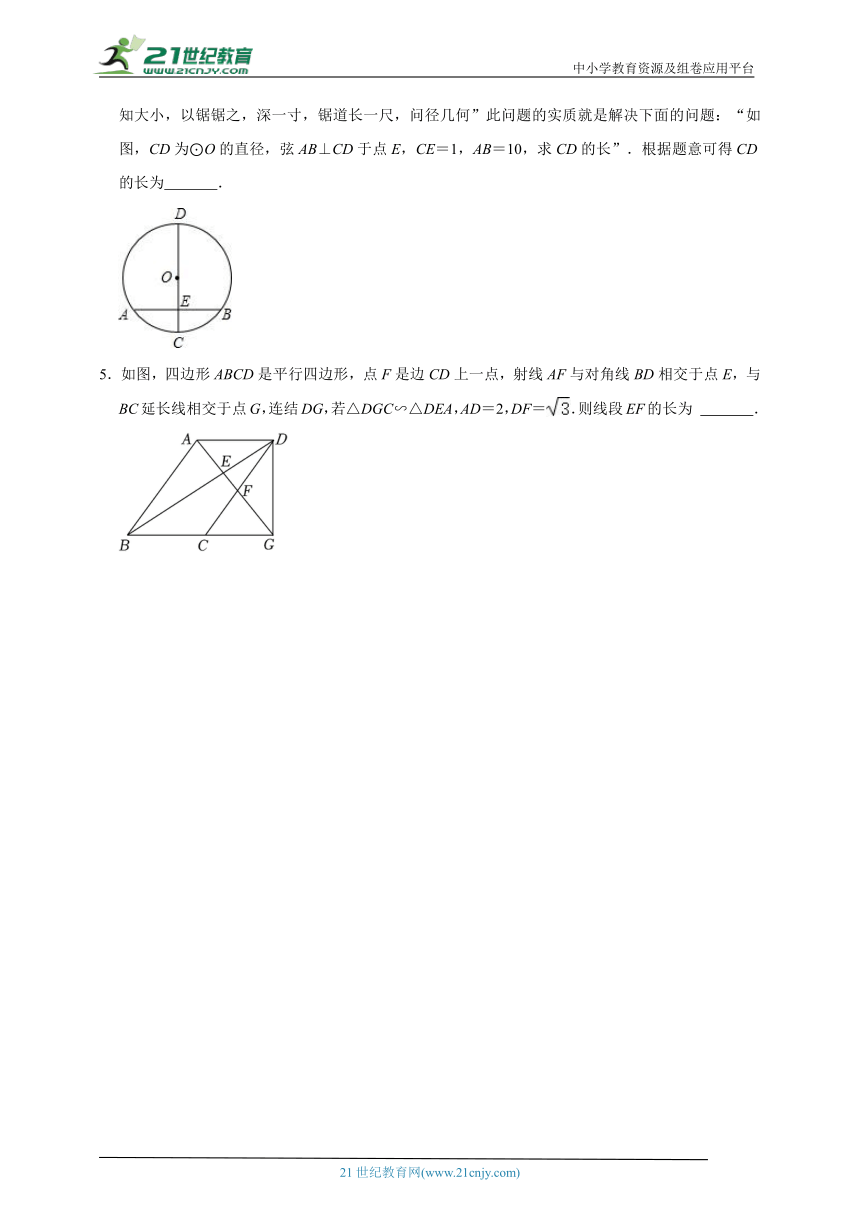
4.“圆材埋壁”是我国古代著名数学著作《九章算术》中的一个问题:“今有圆材,埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问径几何”此问题的实质就是解决下面的问题:“如图,CD为⊙O的直径,弦AB⊥CD于点E,CE=1,AB=10,求CD的长”.根据题意可得CD的长为 .
5.如图,四边形ABCD是平行四边形,点F是边CD上一点,射线AF与对角线BD相交于点E,与BC延长线相交于点G,连结DG,若△DGC∽△DEA,AD=2,DF=.则线段EF的长为 .
浙江省中考数学考前冲刺每日一练18(精选全省各市历年经典真题,包含常考题型、易错题型、 小压轴、大压轴)参考答案与试题解析
一.选择题(共3小题)
1.下列说法正确的个数是( )
①一组数据的众数只有一个;②样本的方差越小,波动性越小,说明样本稳定性越好;③一组数据的中位数一定是这组数据中的某一数据;④一组数据的众数一定比平均数大;⑤一组数据的方差一定是正数.
A.0个 B.1个 C.2个 D.4个
【分析】利用方差、众数和中位数的概念,就可以进行判断.
【解答】解:①一组数据的众数可以有一个也可以有多个,①说法错误;
②样本的方差越小,波动越小,说明样本稳定性越好,②说法正确;
③一组数据的中位数不一定是这组数据中的某一数据,③说法错误;
④一组数据的众数不一定比平均数大,④说法错误;
⑤一组数据的方差一定是正数或0,⑤说法错误,
故选:B.
【点评】本题考查的是方差、众数和中位数的概念,掌握方差反映了一组数据的波动大小,方差越大,波动性越大以及中位数和众数的确定方法是解题的关键.
2.若式子在实数范围内有意义,则x的取值范围是( )
A.x>﹣1 B.x≥﹣1且x≠0 C.x>﹣1且x≠0 D.x≠0
【分析】利用分式分母不为0和二次根式、零指数幂有意义的条件确定关于x的不等式,从而确定答案.
【解答】解:根据题意得:x+1>0且x≠0,
解得:x>﹣1且x≠0,
故选:C.
【点评】此题考查的是分式分母不为0和二次根式、零指数幂有意义的条件,掌握分式和二次根式有意义的条件是解题的关键.
3.如图,二次函数y1=ax2+bx+c的图象与反比例函数y2=的图象交于,B(1,1),C(﹣1,﹣1)三点.对于实数a,b,我们定义符号max{a,b}的意义为:当a≥b时,max{a,b}=a;当a<b时,max{a,b}=b;如max{4,﹣2}=4,max{3,3}=3.若函数y=,则函数y的最小值是( )
A.3 B.1 C.﹣1 D.﹣2
【分析】根据图象可确定x≤﹣1,﹣1<x<0,0<x≤,<x≤1,x>1时,max{y1,y2}的值,进一步即可确定函数y的最小值.
【解答】解:根据图象可知,当x≤﹣1时,max{y1,y2}=y2,
当﹣1<x<0时,max{y1,y2}=y1,
当0<x≤时,max{y1,y2}=y2,
当<x≤1时,max{y1,y2}=y1,
当x>1时,max{y1,y2}=y2,
∴函数y=的最小值为﹣2,
故选:D.
【点评】本题考查了反比例函数和二次函数的综合,分段求出max{y1,y2}的值是解题的关键,注意运用数形结合的思想.
二.填空题(共2小题)
4.“圆材埋壁”是我国古代著名数学著作《九章算术》中的一个问题:“今有圆材,埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问径几何”此问题的实质就是解决下面的问题:“如图,CD为⊙O的直径,弦AB⊥CD于点E,CE=1,AB=10,求CD的长”.根据题意可得CD的长为 26 .
【分析】根据垂径定理和勾股定理求解.
【解答】解:连接OA,AB⊥CD,
由垂径定理知,点E是AB的中点,AE=AB=5,OE=OC﹣CE=OA﹣CE,
设半径为r,由勾股定理得,OA2=AE2+OE2=AE2+(OA﹣CE)2,即r2=52+(r﹣1)2,
解得:r=13,
所以CD=2r=26,
即圆的直径为26.
【点评】本题利用了垂径定理和勾股定理求解.
5.如图,四边形ABCD是平行四边形,点F是边CD上一点,射线AF与对角线BD相交于点E,与BC延长线相交于点G,连结DG,若△DGC∽△DEA,AD=2,DF=.则线段EF的长为 .
【分析】根据平行线的性质和相似三角形的对应角相等可得:∠DCG=∠AGB=∠DAG=∠ADC,则DF=AF=,CF=FG,所以AB=CD=AG,过点A作AM⊥BC于M,过点F作FQ⊥AD于Q,则BM=MG,设MG=x,AM=x,则AG=x,CG=2x﹣2,根据△AED∽△GEB和△DGC∽△DEA,列比例式可得结论.
【解答】解:∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠DAE=∠AGB,∠ADC=∠DCG,
∵△DGC∽△DEA,
∴∠DAE=∠DCG,
∴∠DCG=∠AGB=∠DAG=∠ADC,
∴DF=AF=,CF=FG,
∴AG=CD,
∵AB=CD,
∴AB=AG,
如图,过点A作AM⊥BC于M,过点F作FQ⊥AD于Q,则BM=MG,
∵AF=DF=,AD=2,
∴AQ=DQ=AD=1,
∴FQ=,
∵∠DAG=∠AGB,
∴tan∠DAG=tan∠AGB,
∴==,
设MG=x,AM=x,则AG=x,CG=2x﹣2,
∵AD∥BG,
∴△AED∽△GEB,
∴=,即=,
∴AE=,
∵△DGC∽△DEA,
∴=,即=,
∴x=2(负值舍),
∴EF=AF﹣AE=﹣=.
故答案为:.
【点评】本题考查了平行四边形的性质,相似三角形的性质和判定,等腰三角形的性质和判定,三角函数的定义,勾股定理等知识;涉及知识点较多,有难度,合理添加辅助线,设未知数表示线段的长,并与方程相结合是解题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
浙江省中考数学考前冲刺每日一练18(精选全省各市历年经典真题,包含常考题型、易错题型、 小压轴、大压轴)
1.下列说法正确的个数是( )
①一组数据的众数只有一个;②样本的方差越小,波动性越小,说明样本稳定性越好;③一组数据的中位数一定是这组数据中的某一数据;④一组数据的众数一定比平均数大;⑤一组数据的方差一定是正数.
A.0个 B.1个 C.2个 D.4个
2.若式子在实数范围内有意义,则x的取值范围是( )
A.x>﹣1 B.x≥﹣1且x≠0 C.x>﹣1且x≠0 D.x≠0
3.如图,二次函数y1=ax2+bx+c的图象与反比例函数y2=的图象交于,B(1,1),C(﹣1,﹣1)三点.对于实数a,b,我们定义符号max{a,b}的意义为:当a≥b时,max{a,b}=a;当a<b时,max{a,b}=b;如max{4,﹣2}=4,max{3,3}=3.若函数y=,则函数y的最小值是( )
A.3 B.1 C.﹣1 D.﹣2
4.“圆材埋壁”是我国古代著名数学著作《九章算术》中的一个问题:“今有圆材,埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问径几何”此问题的实质就是解决下面的问题:“如图,CD为⊙O的直径,弦AB⊥CD于点E,CE=1,AB=10,求CD的长”.根据题意可得CD的长为 .
5.如图,四边形ABCD是平行四边形,点F是边CD上一点,射线AF与对角线BD相交于点E,与BC延长线相交于点G,连结DG,若△DGC∽△DEA,AD=2,DF=.则线段EF的长为 .
浙江省中考数学考前冲刺每日一练18(精选全省各市历年经典真题,包含常考题型、易错题型、 小压轴、大压轴)参考答案与试题解析
一.选择题(共3小题)
1.下列说法正确的个数是( )
①一组数据的众数只有一个;②样本的方差越小,波动性越小,说明样本稳定性越好;③一组数据的中位数一定是这组数据中的某一数据;④一组数据的众数一定比平均数大;⑤一组数据的方差一定是正数.
A.0个 B.1个 C.2个 D.4个
【分析】利用方差、众数和中位数的概念,就可以进行判断.
【解答】解:①一组数据的众数可以有一个也可以有多个,①说法错误;
②样本的方差越小,波动越小,说明样本稳定性越好,②说法正确;
③一组数据的中位数不一定是这组数据中的某一数据,③说法错误;
④一组数据的众数不一定比平均数大,④说法错误;
⑤一组数据的方差一定是正数或0,⑤说法错误,
故选:B.
【点评】本题考查的是方差、众数和中位数的概念,掌握方差反映了一组数据的波动大小,方差越大,波动性越大以及中位数和众数的确定方法是解题的关键.
2.若式子在实数范围内有意义,则x的取值范围是( )
A.x>﹣1 B.x≥﹣1且x≠0 C.x>﹣1且x≠0 D.x≠0
【分析】利用分式分母不为0和二次根式、零指数幂有意义的条件确定关于x的不等式,从而确定答案.
【解答】解:根据题意得:x+1>0且x≠0,
解得:x>﹣1且x≠0,
故选:C.
【点评】此题考查的是分式分母不为0和二次根式、零指数幂有意义的条件,掌握分式和二次根式有意义的条件是解题的关键.
3.如图,二次函数y1=ax2+bx+c的图象与反比例函数y2=的图象交于,B(1,1),C(﹣1,﹣1)三点.对于实数a,b,我们定义符号max{a,b}的意义为:当a≥b时,max{a,b}=a;当a<b时,max{a,b}=b;如max{4,﹣2}=4,max{3,3}=3.若函数y=,则函数y的最小值是( )
A.3 B.1 C.﹣1 D.﹣2
【分析】根据图象可确定x≤﹣1,﹣1<x<0,0<x≤,<x≤1,x>1时,max{y1,y2}的值,进一步即可确定函数y的最小值.
【解答】解:根据图象可知,当x≤﹣1时,max{y1,y2}=y2,
当﹣1<x<0时,max{y1,y2}=y1,
当0<x≤时,max{y1,y2}=y2,
当<x≤1时,max{y1,y2}=y1,
当x>1时,max{y1,y2}=y2,
∴函数y=的最小值为﹣2,
故选:D.
【点评】本题考查了反比例函数和二次函数的综合,分段求出max{y1,y2}的值是解题的关键,注意运用数形结合的思想.
二.填空题(共2小题)
4.“圆材埋壁”是我国古代著名数学著作《九章算术》中的一个问题:“今有圆材,埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问径几何”此问题的实质就是解决下面的问题:“如图,CD为⊙O的直径,弦AB⊥CD于点E,CE=1,AB=10,求CD的长”.根据题意可得CD的长为 26 .
【分析】根据垂径定理和勾股定理求解.
【解答】解:连接OA,AB⊥CD,
由垂径定理知,点E是AB的中点,AE=AB=5,OE=OC﹣CE=OA﹣CE,
设半径为r,由勾股定理得,OA2=AE2+OE2=AE2+(OA﹣CE)2,即r2=52+(r﹣1)2,
解得:r=13,
所以CD=2r=26,
即圆的直径为26.
【点评】本题利用了垂径定理和勾股定理求解.
5.如图,四边形ABCD是平行四边形,点F是边CD上一点,射线AF与对角线BD相交于点E,与BC延长线相交于点G,连结DG,若△DGC∽△DEA,AD=2,DF=.则线段EF的长为 .
【分析】根据平行线的性质和相似三角形的对应角相等可得:∠DCG=∠AGB=∠DAG=∠ADC,则DF=AF=,CF=FG,所以AB=CD=AG,过点A作AM⊥BC于M,过点F作FQ⊥AD于Q,则BM=MG,设MG=x,AM=x,则AG=x,CG=2x﹣2,根据△AED∽△GEB和△DGC∽△DEA,列比例式可得结论.
【解答】解:∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠DAE=∠AGB,∠ADC=∠DCG,
∵△DGC∽△DEA,
∴∠DAE=∠DCG,
∴∠DCG=∠AGB=∠DAG=∠ADC,
∴DF=AF=,CF=FG,
∴AG=CD,
∵AB=CD,
∴AB=AG,
如图,过点A作AM⊥BC于M,过点F作FQ⊥AD于Q,则BM=MG,
∵AF=DF=,AD=2,
∴AQ=DQ=AD=1,
∴FQ=,
∵∠DAG=∠AGB,
∴tan∠DAG=tan∠AGB,
∴==,
设MG=x,AM=x,则AG=x,CG=2x﹣2,
∵AD∥BG,
∴△AED∽△GEB,
∴=,即=,
∴AE=,
∵△DGC∽△DEA,
∴=,即=,
∴x=2(负值舍),
∴EF=AF﹣AE=﹣=.
故答案为:.
【点评】本题考查了平行四边形的性质,相似三角形的性质和判定,等腰三角形的性质和判定,三角函数的定义,勾股定理等知识;涉及知识点较多,有难度,合理添加辅助线,设未知数表示线段的长,并与方程相结合是解题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
