浙江省中考数学考前冲刺每日一练19(精选全省各市历年经典真题,包含常考题型、易错题型、 小压轴、大压轴)
文档属性
| 名称 | 浙江省中考数学考前冲刺每日一练19(精选全省各市历年经典真题,包含常考题型、易错题型、 小压轴、大压轴) |  | |
| 格式 | doc | ||
| 文件大小 | 406.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-24 09:27:45 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
浙江省中考数学考前冲刺每日一练19(精选全省各市历年经典真题,包含常考题型、易错题型、 小压轴、大压轴)
1.《九章算术》是古代中国第一部自成体系的数学专著,其中《卷第八方程》记载:“今有甲乙二人持钱不知其数,甲得乙半而钱五十,乙得甲太半而亦钱五十,问甲、乙持钱各几何?”译文是:今有甲、乙两人持钱不知道各有多少,甲若得到乙所有钱的,则甲有50钱,乙若得到甲所有钱的,则乙也有50钱.问甲、乙各持钱多少?设甲持钱数为x钱,乙持钱数为y钱,列出关于x、y的二元一次方程组是( )
A. B.
C. D.
2.如图,在锐角三角形△ABC中,分别以三边AB,BC,CA为直径作圆.记三角形外的阴影面积为S1,三角形内的阴影面积为S2,在以下四个选项的条件中,不一定能求出S1﹣S2的是( )
A.已知△ABC的三条中位线的长度
B.已知△ABC的面积
C.已知BC的长度,以及AB,AC的长度和
D.已知AB,AC的长度及∠ACB的度数
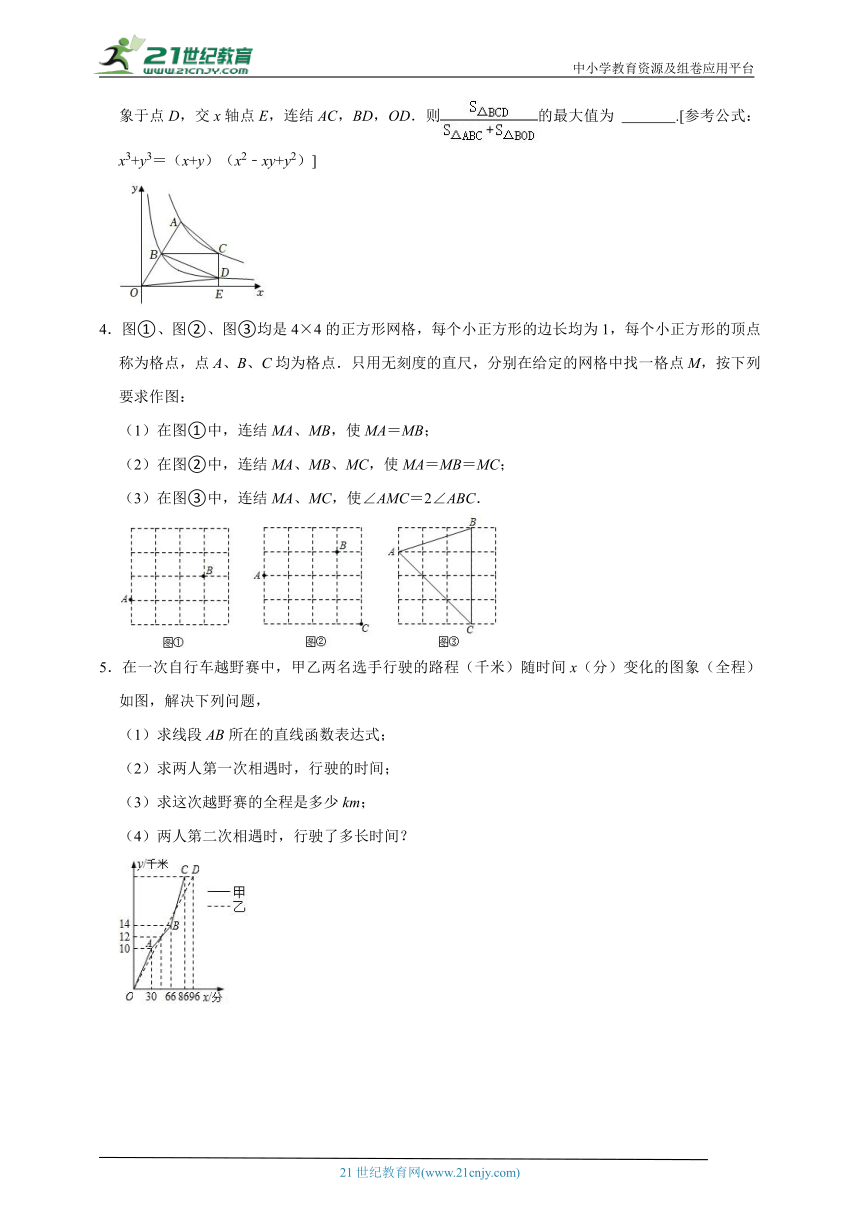
3.如图,在反比例函数y=(x>0)的图象上有动点A,连结OA,y=(x>0)的图象经过OA上的中点B,过点B作BC∥x轴交函数y=的图象于点C,过点C作CE∥y轴交函数y=的图象于点D,交x轴点E,连结AC,BD,OD.则的最大值为 .[参考公式:x3+y3=(x+y)(x2﹣xy+y2)]
4.图①、图②、图③均是4×4的正方形网格,每个小正方形的边长均为1,每个小正方形的顶点称为格点,点A、B、C均为格点.只用无刻度的直尺,分别在给定的网格中找一格点M,按下列要求作图:
(1)在图①中,连结MA、MB,使MA=MB;
(2)在图②中,连结MA、MB、MC,使MA=MB=MC;
(3)在图③中,连结MA、MC,使∠AMC=2∠ABC.
5.在一次自行车越野赛中,甲乙两名选手行驶的路程(千米)随时间x(分)变化的图象(全程)如图,解决下列问题,
(1)求线段AB所在的直线函数表达式;
(2)求两人第一次相遇时,行驶的时间;
(3)求这次越野赛的全程是多少km;
(4)两人第二次相遇时,行驶了多长时间?
浙江省中考数学考前冲刺每日一练19(精选全省各市历年经典真题,包含常考题型、易错题型、 小压轴、大压轴)参考答案与试题解析
一.选择题(共2小题)
1.《九章算术》是古代中国第一部自成体系的数学专著,其中《卷第八方程》记载:“今有甲乙二人持钱不知其数,甲得乙半而钱五十,乙得甲太半而亦钱五十,问甲、乙持钱各几何?”译文是:今有甲、乙两人持钱不知道各有多少,甲若得到乙所有钱的,则甲有50钱,乙若得到甲所有钱的,则乙也有50钱.问甲、乙各持钱多少?设甲持钱数为x钱,乙持钱数为y钱,列出关于x、y的二元一次方程组是( )
A. B.
C. D.
【分析】根据“甲若得到乙所有钱的,则甲有50钱,乙若得到甲所有钱的,则乙也有50钱”,列出二元一次方程组解答即可.
【解答】解:设甲、乙的持钱数分别为x,y,
根据题意可得:,
故选:B.
【点评】本题考查了由实际问题抽象出二元一次方程组,正确找出等量关系,列出二元一次方程组是解题的关键.
2.如图,在锐角三角形△ABC中,分别以三边AB,BC,CA为直径作圆.记三角形外的阴影面积为S1,三角形内的阴影面积为S2,在以下四个选项的条件中,不一定能求出S1﹣S2的是( )
A.已知△ABC的三条中位线的长度
B.已知△ABC的面积
C.已知BC的长度,以及AB,AC的长度和
D.已知AB,AC的长度及∠ACB的度数
【分析】由题意S1=S3个半外圆﹣S6个弓形=S3个外半圆﹣(S3个内半圆﹣2S△ABC﹣S2)推出S1=2S△ABC+S2,推出S1﹣S2=2S△ABC.再一一判断即可.
【解答】解:∵S1=S3个半外圆﹣S6个弓形=S3个外半圆﹣(S3个内半圆﹣2S△ABC﹣S2),
∴S1=2S△ABC+S2,
∴S1﹣S2=2S△ABC.
A:若已知△ABC的三条中位线的长度,即可得到△ABC三边的长度,再根据海伦公式S=(a,b,c是三角形的三边,p=(a+b+c)),据此求得三角形的面积,即可得到S1﹣S2的值,故A选项不符合题意;B:已知△ABC的面积,代入S1﹣S2=2S△ABC即可求得,故B选项不符合题意;
C:∵已知AB,AC两边长度和,
∴AB,AC的长度不确定,
∴△ABC的面积也不确定,
∴不一定能求出S1﹣S2的值,故C选项符合题意;
D:如解图,过点A作AD⊥BC于点D.
∵AD=AC sin∠ACB,
在△ADC和△ADB中,
∴CD=,BD=,
∴S△ABC= AD (BD+CD),据此即可求得S1﹣S2的值,故D选项不符合题意.
故选C.
【点评】本题三角形综合题,考查了三角形的面积,圆等知识,解题的关键是学会用割补法求阴影部分的面积,本题的突破点是证明S1﹣S2=2S△ABC.
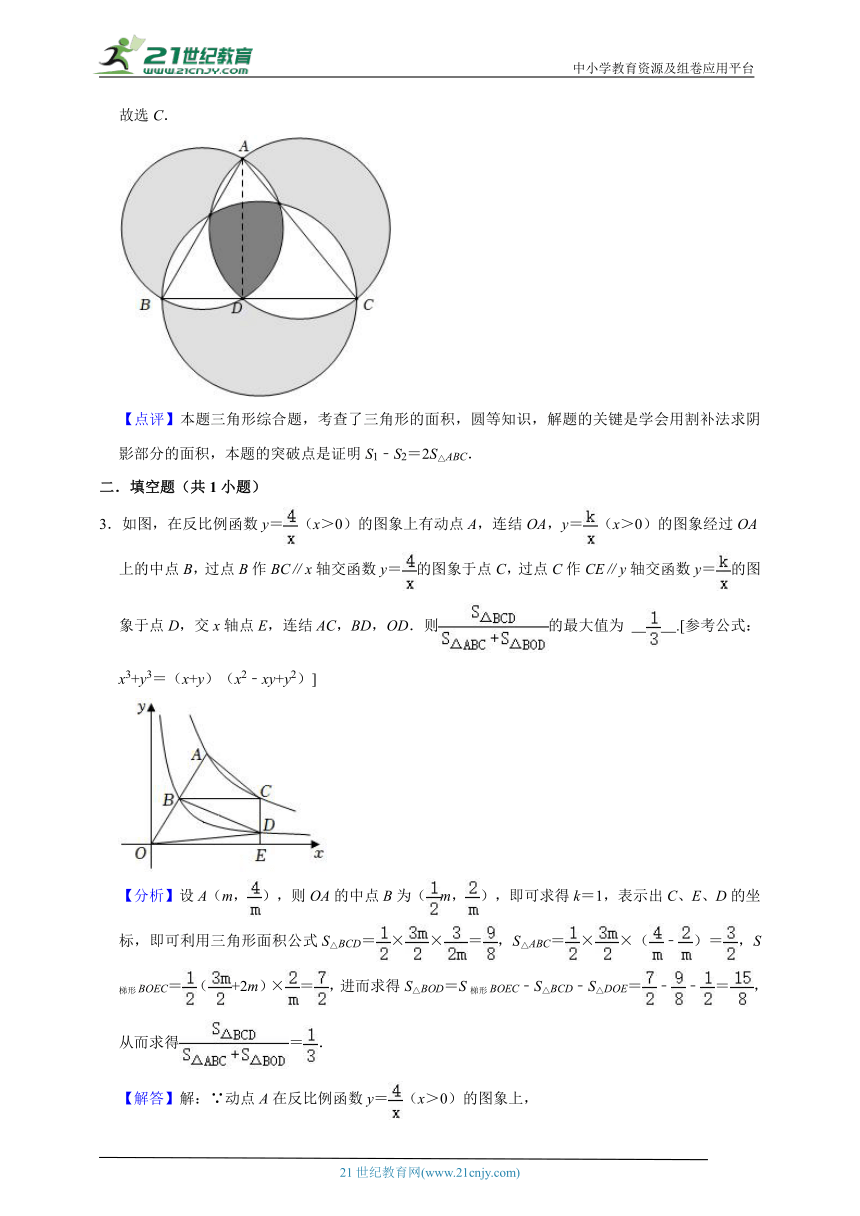
二.填空题(共1小题)
3.如图,在反比例函数y=(x>0)的图象上有动点A,连结OA,y=(x>0)的图象经过OA上的中点B,过点B作BC∥x轴交函数y=的图象于点C,过点C作CE∥y轴交函数y=的图象于点D,交x轴点E,连结AC,BD,OD.则的最大值为 .[参考公式:x3+y3=(x+y)(x2﹣xy+y2)]
【分析】设A(m,),则OA的中点B为(m,),即可求得k=1,表示出C、E、D的坐标,即可利用三角形面积公式S△BCD=××=,S△ABC=××(﹣)=,S梯形BOEC=(+2m)×=,进而求得S△BOD=S梯形BOEC﹣S△BCD﹣S△DOE=﹣﹣=,从而求得=.
【解答】解:∵动点A在反比例函数y=(x>0)的图象上,
∴设A(m,),
∴OA的中点B为(m,),
∵y=(x>0)的图象经过点B,
∴k=m =1,
∴y=,
∵过点B作BC∥x轴交函数y=的图象于点C,
∴C的纵坐标y=,
把y=代入y=得,x=2m,
∴C(2m,),E(2m,0),
把x=2m代入y=得,y=,
∴D(2m,),
∴BC=2m﹣m=,CD=﹣=,
∴S△BCD=××=,S△ABC=××(﹣)=,S梯形BOEC=(+2m)×=,
∵S△DOE=×1=,
∴S△BOD=S梯形BOEC﹣S△BCD﹣S△DOE=﹣﹣=,
∴==,
故答案为:.
【点评】本题考查反比例函数图象上点的坐标特征,反比例函数系数k的几何意义,待定系数法求反比例函数的解析式,解题的关键是学会利用参数解决问题,属于中考填空题中的压轴题.
三.解答题(共2小题)
4.图①、图②、图③均是4×4的正方形网格,每个小正方形的边长均为1,每个小正方形的顶点称为格点,点A、B、C均为格点.只用无刻度的直尺,分别在给定的网格中找一格点M,按下列要求作图:
(1)在图①中,连结MA、MB,使MA=MB;
(2)在图②中,连结MA、MB、MC,使MA=MB=MC;
(3)在图③中,连结MA、MC,使∠AMC=2∠ABC.
【分析】(1)根据勾股定理得MA=MB=.
(2)连接AC,取AC中点M,MA=MB=MC=.
(3)取△ABC外心M,由圆周角定理得∠AMC=2∠ABC.
【解答】解:如图,
【点评】本题考查网格作图问题,解题关键是熟练掌握直角三角形与圆的性质.
5.在一次自行车越野赛中,甲乙两名选手行驶的路程(千米)随时间x(分)变化的图象(全程)如图,解决下列问题,
(1)求线段AB所在的直线函数表达式;
(2)求两人第一次相遇时,行驶的时间;
(3)求这次越野赛的全程是多少km;
(4)两人第二次相遇时,行驶了多长时间?
【分析】(1)设线段AB所在的直线函数表达式为y=kx+b,用待定系数法即得线段AB所在的直线函数表达式为y=x+;
(2)在y=x+中,令y=12解得x的值即可得两人第一次相遇时,行驶的时间是48分钟;
(3)由(2)可知,乙用48分钟行驶了12km,即可得这次越野赛的全程是24km;
(4)求出直线BC的解析式为y=x﹣19,直线OD解析式为y=x,再求它们交点坐标即可得答案.
【解答】解:(1)设线段AB所在的直线函数表达式为y=kx+b,将A(30,10),B(66,14)代入得:
,
解得,
∴线段AB所在的直线函数表达式为y=x+;
(2)在y=x+中,令y=12得:
x+=12,
解得x=48,
答:两人第一次相遇时,行驶的时间是48分钟;
(3)由(2)可知,乙用48分钟行驶了12km,
∴这次越野赛的全程是×96=24(km),
答:这次越野赛的全程是24km;
(4)由(3)知C(86,24),
∵B(66,14),
∴直线BC的解析式为y=x﹣19,
由O(0,0),D(96,24)得直线OD解析式为y=x,
解得,
答:两人第二次相遇时,行驶了76分钟.
【点评】本题考查一次函数的应用,解题的关键是读懂题意,能正确识图,用待定系数法求出相关函数解析式.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
浙江省中考数学考前冲刺每日一练19(精选全省各市历年经典真题,包含常考题型、易错题型、 小压轴、大压轴)
1.《九章算术》是古代中国第一部自成体系的数学专著,其中《卷第八方程》记载:“今有甲乙二人持钱不知其数,甲得乙半而钱五十,乙得甲太半而亦钱五十,问甲、乙持钱各几何?”译文是:今有甲、乙两人持钱不知道各有多少,甲若得到乙所有钱的,则甲有50钱,乙若得到甲所有钱的,则乙也有50钱.问甲、乙各持钱多少?设甲持钱数为x钱,乙持钱数为y钱,列出关于x、y的二元一次方程组是( )
A. B.
C. D.
2.如图,在锐角三角形△ABC中,分别以三边AB,BC,CA为直径作圆.记三角形外的阴影面积为S1,三角形内的阴影面积为S2,在以下四个选项的条件中,不一定能求出S1﹣S2的是( )
A.已知△ABC的三条中位线的长度
B.已知△ABC的面积
C.已知BC的长度,以及AB,AC的长度和
D.已知AB,AC的长度及∠ACB的度数
3.如图,在反比例函数y=(x>0)的图象上有动点A,连结OA,y=(x>0)的图象经过OA上的中点B,过点B作BC∥x轴交函数y=的图象于点C,过点C作CE∥y轴交函数y=的图象于点D,交x轴点E,连结AC,BD,OD.则的最大值为 .[参考公式:x3+y3=(x+y)(x2﹣xy+y2)]
4.图①、图②、图③均是4×4的正方形网格,每个小正方形的边长均为1,每个小正方形的顶点称为格点,点A、B、C均为格点.只用无刻度的直尺,分别在给定的网格中找一格点M,按下列要求作图:
(1)在图①中,连结MA、MB,使MA=MB;
(2)在图②中,连结MA、MB、MC,使MA=MB=MC;
(3)在图③中,连结MA、MC,使∠AMC=2∠ABC.
5.在一次自行车越野赛中,甲乙两名选手行驶的路程(千米)随时间x(分)变化的图象(全程)如图,解决下列问题,
(1)求线段AB所在的直线函数表达式;
(2)求两人第一次相遇时,行驶的时间;
(3)求这次越野赛的全程是多少km;
(4)两人第二次相遇时,行驶了多长时间?
浙江省中考数学考前冲刺每日一练19(精选全省各市历年经典真题,包含常考题型、易错题型、 小压轴、大压轴)参考答案与试题解析
一.选择题(共2小题)
1.《九章算术》是古代中国第一部自成体系的数学专著,其中《卷第八方程》记载:“今有甲乙二人持钱不知其数,甲得乙半而钱五十,乙得甲太半而亦钱五十,问甲、乙持钱各几何?”译文是:今有甲、乙两人持钱不知道各有多少,甲若得到乙所有钱的,则甲有50钱,乙若得到甲所有钱的,则乙也有50钱.问甲、乙各持钱多少?设甲持钱数为x钱,乙持钱数为y钱,列出关于x、y的二元一次方程组是( )
A. B.
C. D.
【分析】根据“甲若得到乙所有钱的,则甲有50钱,乙若得到甲所有钱的,则乙也有50钱”,列出二元一次方程组解答即可.
【解答】解:设甲、乙的持钱数分别为x,y,
根据题意可得:,
故选:B.
【点评】本题考查了由实际问题抽象出二元一次方程组,正确找出等量关系,列出二元一次方程组是解题的关键.
2.如图,在锐角三角形△ABC中,分别以三边AB,BC,CA为直径作圆.记三角形外的阴影面积为S1,三角形内的阴影面积为S2,在以下四个选项的条件中,不一定能求出S1﹣S2的是( )
A.已知△ABC的三条中位线的长度
B.已知△ABC的面积
C.已知BC的长度,以及AB,AC的长度和
D.已知AB,AC的长度及∠ACB的度数
【分析】由题意S1=S3个半外圆﹣S6个弓形=S3个外半圆﹣(S3个内半圆﹣2S△ABC﹣S2)推出S1=2S△ABC+S2,推出S1﹣S2=2S△ABC.再一一判断即可.
【解答】解:∵S1=S3个半外圆﹣S6个弓形=S3个外半圆﹣(S3个内半圆﹣2S△ABC﹣S2),
∴S1=2S△ABC+S2,
∴S1﹣S2=2S△ABC.
A:若已知△ABC的三条中位线的长度,即可得到△ABC三边的长度,再根据海伦公式S=(a,b,c是三角形的三边,p=(a+b+c)),据此求得三角形的面积,即可得到S1﹣S2的值,故A选项不符合题意;B:已知△ABC的面积,代入S1﹣S2=2S△ABC即可求得,故B选项不符合题意;
C:∵已知AB,AC两边长度和,
∴AB,AC的长度不确定,
∴△ABC的面积也不确定,
∴不一定能求出S1﹣S2的值,故C选项符合题意;
D:如解图,过点A作AD⊥BC于点D.
∵AD=AC sin∠ACB,
在△ADC和△ADB中,
∴CD=,BD=,
∴S△ABC= AD (BD+CD),据此即可求得S1﹣S2的值,故D选项不符合题意.
故选C.
【点评】本题三角形综合题,考查了三角形的面积,圆等知识,解题的关键是学会用割补法求阴影部分的面积,本题的突破点是证明S1﹣S2=2S△ABC.
二.填空题(共1小题)
3.如图,在反比例函数y=(x>0)的图象上有动点A,连结OA,y=(x>0)的图象经过OA上的中点B,过点B作BC∥x轴交函数y=的图象于点C,过点C作CE∥y轴交函数y=的图象于点D,交x轴点E,连结AC,BD,OD.则的最大值为 .[参考公式:x3+y3=(x+y)(x2﹣xy+y2)]
【分析】设A(m,),则OA的中点B为(m,),即可求得k=1,表示出C、E、D的坐标,即可利用三角形面积公式S△BCD=××=,S△ABC=××(﹣)=,S梯形BOEC=(+2m)×=,进而求得S△BOD=S梯形BOEC﹣S△BCD﹣S△DOE=﹣﹣=,从而求得=.
【解答】解:∵动点A在反比例函数y=(x>0)的图象上,
∴设A(m,),
∴OA的中点B为(m,),
∵y=(x>0)的图象经过点B,
∴k=m =1,
∴y=,
∵过点B作BC∥x轴交函数y=的图象于点C,
∴C的纵坐标y=,
把y=代入y=得,x=2m,
∴C(2m,),E(2m,0),
把x=2m代入y=得,y=,
∴D(2m,),
∴BC=2m﹣m=,CD=﹣=,
∴S△BCD=××=,S△ABC=××(﹣)=,S梯形BOEC=(+2m)×=,
∵S△DOE=×1=,
∴S△BOD=S梯形BOEC﹣S△BCD﹣S△DOE=﹣﹣=,
∴==,
故答案为:.
【点评】本题考查反比例函数图象上点的坐标特征,反比例函数系数k的几何意义,待定系数法求反比例函数的解析式,解题的关键是学会利用参数解决问题,属于中考填空题中的压轴题.
三.解答题(共2小题)
4.图①、图②、图③均是4×4的正方形网格,每个小正方形的边长均为1,每个小正方形的顶点称为格点,点A、B、C均为格点.只用无刻度的直尺,分别在给定的网格中找一格点M,按下列要求作图:
(1)在图①中,连结MA、MB,使MA=MB;
(2)在图②中,连结MA、MB、MC,使MA=MB=MC;
(3)在图③中,连结MA、MC,使∠AMC=2∠ABC.
【分析】(1)根据勾股定理得MA=MB=.
(2)连接AC,取AC中点M,MA=MB=MC=.
(3)取△ABC外心M,由圆周角定理得∠AMC=2∠ABC.
【解答】解:如图,
【点评】本题考查网格作图问题,解题关键是熟练掌握直角三角形与圆的性质.
5.在一次自行车越野赛中,甲乙两名选手行驶的路程(千米)随时间x(分)变化的图象(全程)如图,解决下列问题,
(1)求线段AB所在的直线函数表达式;
(2)求两人第一次相遇时,行驶的时间;
(3)求这次越野赛的全程是多少km;
(4)两人第二次相遇时,行驶了多长时间?
【分析】(1)设线段AB所在的直线函数表达式为y=kx+b,用待定系数法即得线段AB所在的直线函数表达式为y=x+;
(2)在y=x+中,令y=12解得x的值即可得两人第一次相遇时,行驶的时间是48分钟;
(3)由(2)可知,乙用48分钟行驶了12km,即可得这次越野赛的全程是24km;
(4)求出直线BC的解析式为y=x﹣19,直线OD解析式为y=x,再求它们交点坐标即可得答案.
【解答】解:(1)设线段AB所在的直线函数表达式为y=kx+b,将A(30,10),B(66,14)代入得:
,
解得,
∴线段AB所在的直线函数表达式为y=x+;
(2)在y=x+中,令y=12得:
x+=12,
解得x=48,
答:两人第一次相遇时,行驶的时间是48分钟;
(3)由(2)可知,乙用48分钟行驶了12km,
∴这次越野赛的全程是×96=24(km),
答:这次越野赛的全程是24km;
(4)由(3)知C(86,24),
∵B(66,14),
∴直线BC的解析式为y=x﹣19,
由O(0,0),D(96,24)得直线OD解析式为y=x,
解得,
答:两人第二次相遇时,行驶了76分钟.
【点评】本题考查一次函数的应用,解题的关键是读懂题意,能正确识图,用待定系数法求出相关函数解析式.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
