华师大版八年级数学下册第十九章 矩形、菱形与正方形 练习 含解析
文档属性
| 名称 | 华师大版八年级数学下册第十九章 矩形、菱形与正方形 练习 含解析 |

|
|
| 格式 | docx | ||
| 文件大小 | 530.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-24 00:00:00 | ||
图片预览


文档简介
华师大版八年级数学下册第十九章练习
一、选择题
1.如图,四边形ABCD是平行四边形,下列说法不正确的是( )
A.当AC=BD时,四边形ABCD是矩形
B.当AB=BC时,四边形ABCD是菱形
C.当AC平分∠BAD时,四边形ABCD是菱形
D.当∠DAB= 90°时,四边形ABCD是正方形
2.菱形不具有的性质是( )
A.对角相等 B.对边平行
C.对角线互相垂直 D.对角线相等
3.关于矩形的性质、下面说法错误的是( )
A.矩形的四个角都是直角
B.矩形的两组对边分别相等
C.矩形的两组对边分别平行
D.矩形的对角线互相垂直平分且相等
4.如图,在菱形ABCD中,∠B=60°,连接AC,若AC=6,则菱形ABCD的周长为( )
A.24 B.30 C. D.
5.如图,在面积为S的菱形ABCD中,对角线AC,BD相交于点O,E,F,G分别是BC,OB,OC的中点,则四边形EFOG的面积为( )
A. B. C. D.
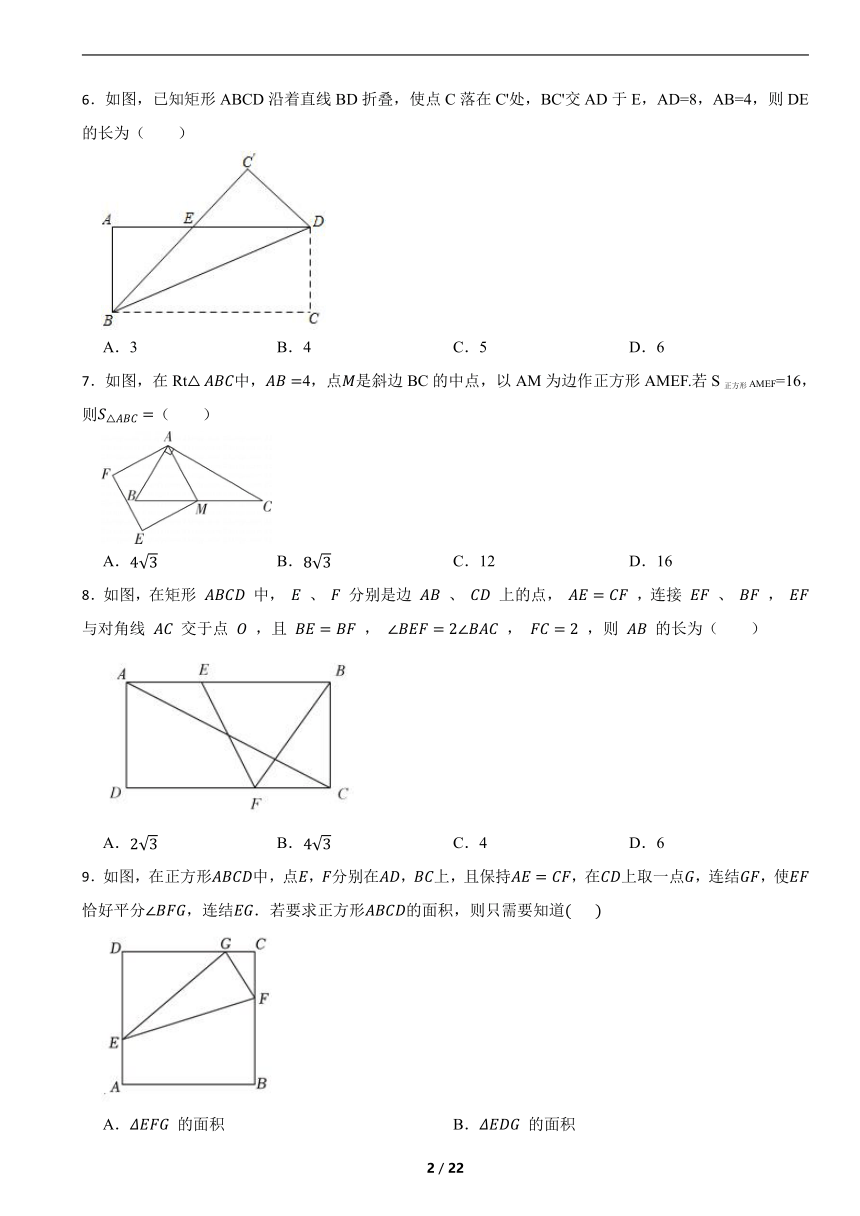
6.如图,已知矩形ABCD沿着直线BD折叠,使点C落在C'处,BC'交AD于E,AD=8,AB=4,则DE的长为( )
A.3 B.4 C.5 D.6
7.如图,在Rt中,4,点是斜边BC的中点,以AM为边作正方形AMEF.若S正方形AMEF=16,则( )
A. B. C.12 D.16
8.如图,在矩形 中, 、 分别是边 、 上的点, ,连接 、 , 与对角线 交于点 ,且 , , ,则 的长为( )
A. B. C.4 D.6
9.如图,在正方形中,点,分别在,上,且保持,在上取一点,连结,使恰好平分,连结.若要求正方形的面积,则只需要知道
A. 的面积 B. 的面积
C. 的周长 D. 的周长
10.如图,正方形 的面积为 , 是等边三角形,点 在正方形 内,在对角线 上有一点 ,使 的和最小,则这个最小值为( ).
A. B. C. D.
二、填空题
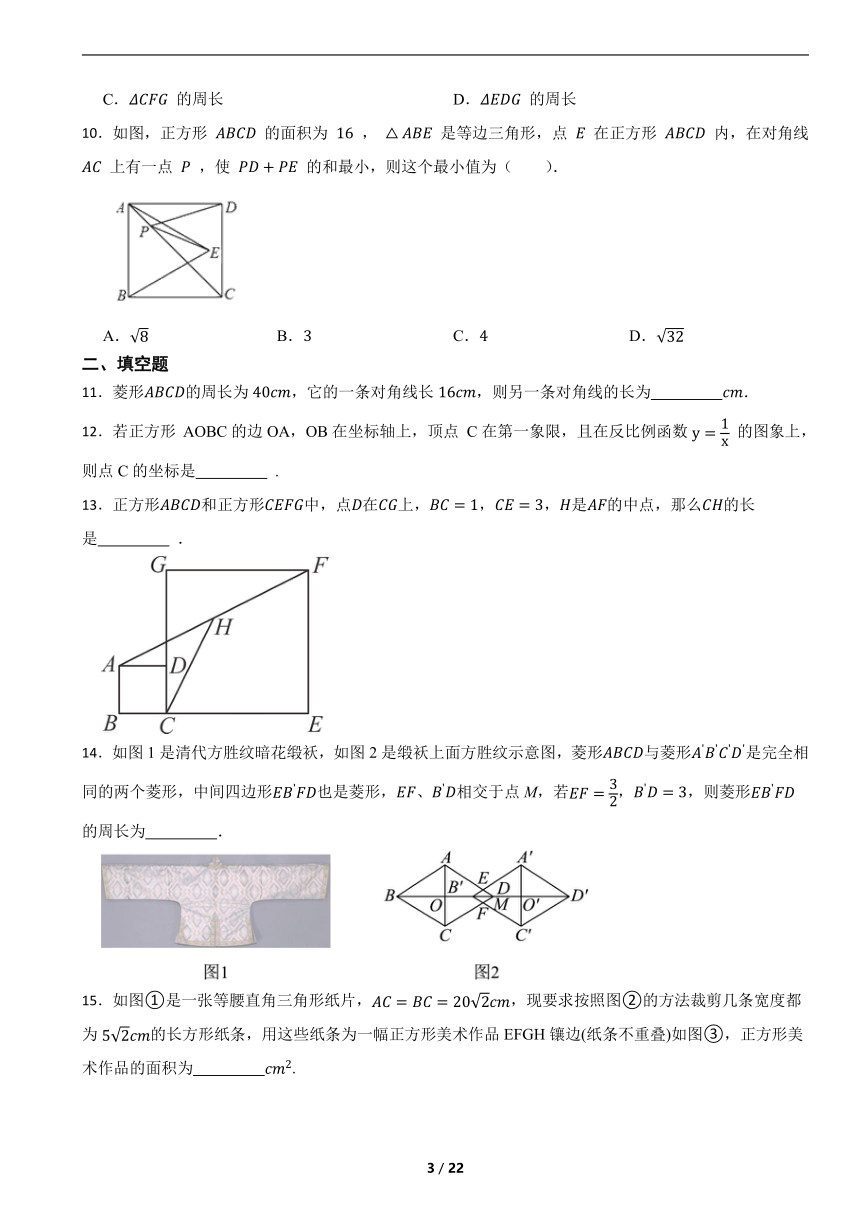
11.菱形的周长为,它的一条对角线长,则另一条对角线的长为 .
12.若正方形 AOBC的边OA,OB在坐标轴上,顶点 C在第一象限,且在反比例函数 的图象上,则点C的坐标是 .
13.正方形和正方形中,点在上,,,是的中点,那么的长是 .
14.如图1是清代方胜纹暗花缎袄,如图2是缎袄上面方胜纹示意图,菱形与菱形是完全相同的两个菱形,中间四边形也是菱形,、相交于点M,若,,则菱形的周长为 .
15.如图①是一张等腰直角三角形纸片,,现要求按照图②的方法裁剪几条宽度都为的长方形纸条,用这些纸条为一幅正方形美术作品EFGH镶边(纸条不重叠)如图③,正方形美术作品的面积为 .
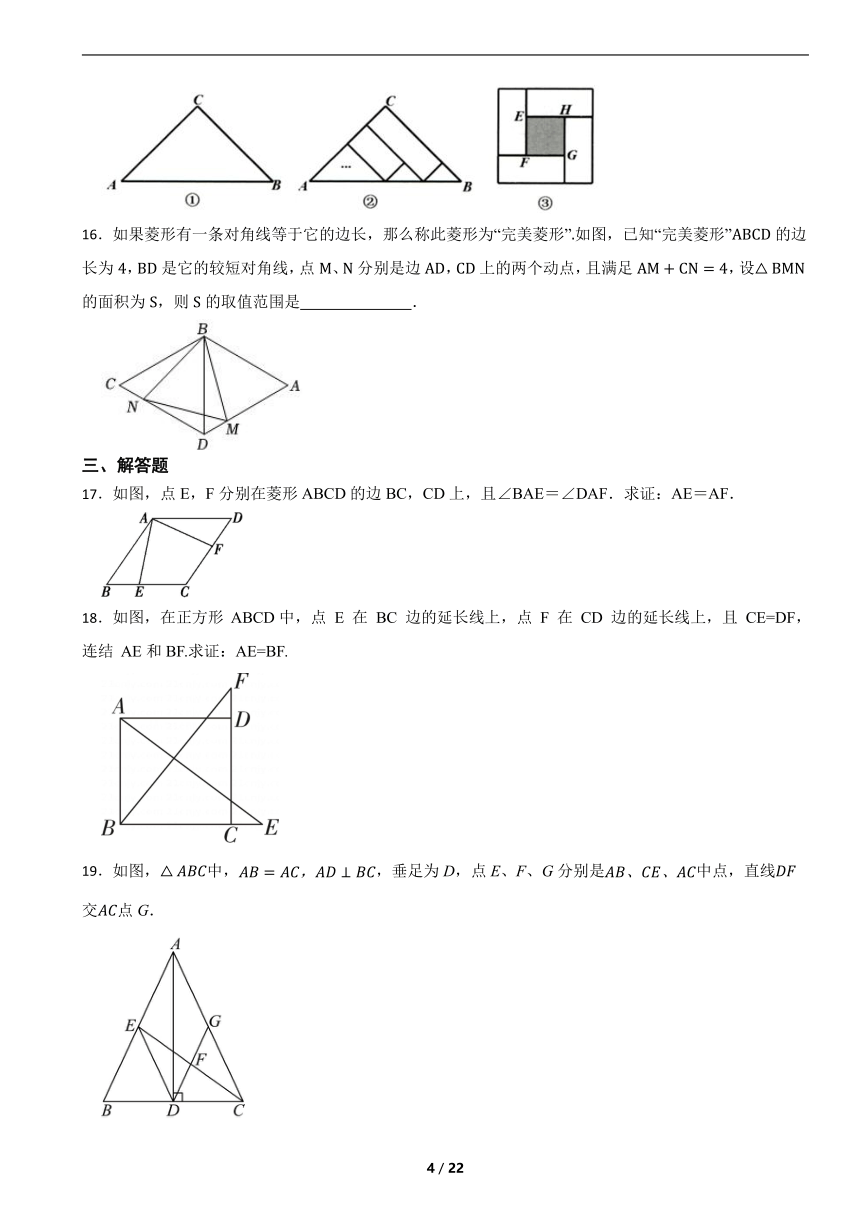
16.如果菱形有一条对角线等于它的边长,那么称此菱形为“完美菱形”如图,已知“完美菱形”的边长为,是它的较短对角线,点、分别是边,上的两个动点,且满足,设的面积为,则的取值范围是 .
三、解答题
17.如图,点E,F分别在菱形ABCD的边BC,CD上,且∠BAE=∠DAF.求证:AE=AF.
18.如图,在正方形 ABCD中,点 E 在 BC 边的延长线上,点 F 在 CD 边的延长线上,且 CE=DF,连结 AE和BF.求证:AE=BF.
19.如图,中,,垂足为D,点E、F、G分别是中点,直线交点G.
(1)求证:四边形是菱形;
(2)若,求的度数.
20.如图,在□ABCD中,点E,F分别在边BC,AD上,连接AE,CF,过点E作于点H,过点F作于点G.
(1)请你添加一个条件: ▲,使四边形EGFH为矩形,并给出证明.
(2)在(1)的条件下,若,,,求AG的长.
21.如图,已知在正方形中,,点为线段上一点点不与、重合,连接,过点作交射线于点,以、为邻边作矩形.
(1)求证:;
(2)连接,设,的面积为求关于的函数关系式并写出自变量的取值范围;
(3)当时,求的度数.
22.如图,矩形的顶点,在轴的正半轴上,点的坐标为,点在点的右侧,反比例函数在第一象限内的图象与直线交于点,交于点.
(1)求点的坐标及反比例函数的关系式;
(2)连接,若矩形的面积是27,求出的面积.
23.【中考预测】
(1)如图1,在正方形ABCD中,△AEF的顶点E,F分别在边BC,CD上,高线AG与正方形的边长相等,求∠EAF的度数.
(2)在图1中,若EG=4,GF=6,求正方形ABCD的边长.
(3)如图2,在Rt△ABD中,AD,M,N是边BD上的任意两点,且∠MAN=45°,将△ABM绕点A逆时针旋转90°至△ADH的位置,连结NH,试判断MN ,ND ,DH 之间的数量关系,并说明理由.
答案解析部分
1.【答案】D
【解析】【解答】解:①对角线相等的平行四边形是矩形,故A正确;
②有一组邻边相等的平行四边形是菱形,故B正确;
③∵AC平分∠BAD,
∴∠DAC=∠CAB,
∵CD∥AB,
∴∠DCA=∠CAB,
∴∠DAC=∠DCA,
∴DA=DC,
∴平行四边形ABCD是菱形,故C正确;
④当∠DAB=90°,平行四边形ABCD是矩形,不能判定其是正方形,故D错误;
故答案为:D.
【分析】通过矩形、菱形、矩形及正方形的判定方法一 一判断即可.
2.【答案】D
【解析】【解答】解:A、菱形是特殊的平行四边形,其对角是相等的,故此选项不符合题意;
B、菱形是特殊的平行四边形,其对边是互相平行的,故此选项不符合题意;
C、菱形的对角线互相垂直且平分,每一条对角线平分一组对角,故此选项不符合题意;
D、菱形的对角线只是互相垂直且平分,每一条对角线平分一组对角,不一定相等,故此选项符合题意.
故答案为:D.
【分析】菱形是特殊的平行四边形,具有对角相等、对边平行、四条边相等、对角线互相垂直且平分,每一条对角线平分一组对角,据此逐项判断即可得解.
3.【答案】D
【解析】【解答】A、∵矩形的四个角都是直角,∴A正确,不符合题意;
B、∵矩形的两组对边分别相等,∴B正确,不符合题意;
C、∵矩形的两组对边分别平行,∴C正确,不符合题意;
D、∵矩形的对角线互相平分且相等但不垂直,∴D不正确,符合题意;
故答案为:D.
【分析】利用矩形的性质逐项分析判断即可.
4.【答案】A
【解析】【解答】解:∵四边形ABCD是菱形,
∴AB=BC=CD=AD.
∵∠B=60°,
∴△ABC是等边三角形.
∴AB=AC=6,
故菱形的周长是4×6=24.
故答案为:A.
【分析】根据菱形的性质和∠B的度数判断△ABC是等边三角形,从而得到AB=AC=6,于是可得周长.
5.【答案】B
【解析】【解答】解:如图所示,连接OE,
∵四边形ABCD是菱形,
∴∠BOC=90°,
又∵E是BC的中点,
∴OE=BE=CE,
又∵F,G分别是BO,CO的中点,
∴EF⊥OB,EG⊥OC,
∴四边形OGEF是矩形,
∵菱形ABCD的面积为S,
∴AC×BD=S,即AC×BD=2S,
∴四边形EFOG的面积=OG×OF=OC×OB=AC×BD=AC×BD=×2S=S.
故答案为:B.
【分析】连接OE,根据菱形的性质及等腰三角形的性质,即可得出EF⊥OB,EG⊥OC,推出四边形OGEF是矩形,再根据菱形的面积即可得出矩形的面积。
6.【答案】C
【解析】【解答】解:∵四边形ABCD是矩形,
∴AB=CD,∠C=∠A=90°
由折叠的性质可得:C'D=CD=AB;∠C'=∠C=∠A
在△ABE与△C'ED中
∴△ABE≌△C'ED(AAS)
∴DE=BE
设DE=BE=x,则AE=8-x,AB=4,在直角三角形ABE中,
解得x=5
故答案为:C.
【分析】由矩形性质得AB=CD,∠C=∠A=90°,利用折叠的性质得C'D=CD=AB,∠C'=∠C=∠A;再利用AAS证明△ABE≌△C'ED,利用全等三角形的对应边相等,可证得DE=BE,设DE=BE=x,可表示出AE的长,然后利用勾股定理建立关于x的方程,解方程求出x的值.
7.【答案】B
【解析】【解答】解:∵四边形AMEF是正方形,S正方形AMEF=16,
∴AM2=16,
∴AM=4,
在Rt△ABC中,点M是斜边BC的中点,
∴,
即BC=2AM=8,
在Rt△ABC中,AB=4,
∴,
∴,
故答案为:B.
【分析】先根据正方形AMEF的面积求出AM的长,然后根据直角三角形斜边上的中线等于斜边的一半求出BC的长,在Rt△ABC中通过勾股定理求出AC的长,最后利用直角三角形的面积公式可求出△ABC的面积即可解答.
8.【答案】D
【解析】【解答】解:如图,连接BO,
∵四边形ABCD是矩形,
∴DC∥AB,∠DCB=90°
∴∠FCO=∠EAO,
在△AOE和△COF中,
,
∴△AOE≌△COF,
∴OE=OF,OA=OC,
∵BF=BE,
∴BO⊥EF,∠BOF=90°,
∵∠FEB=2∠CAB=∠CAB+∠AOE,
∴∠EAO=∠EOA,
∴EA=EO=OF=FC=2,
在Rt△BFO和Rt△BFC中,
,
∴Rt△BFO≌Rt△BFC,
∴BO=BC,
在Rt△ABC中,∵AO=OC,
∴BO=AO=OC=BC,
∴△BOC是等边三角形,
∴∠BCO=60°,∠BAC=30°,
∴∠FEB=2∠CAB=60°,
∵BE=BF,
∴△BEF是等边三角形,
∴EB=EF=4,
∴AB=AE+EB=2+4=6.
故答案为:D.
【分析】连接BO,根据矩形的性质可得DC∥AB,∠DCB=90°,根据平行线的性质可得∠FCO=∠EAO,证明△AOE≌△COF,得到OE=OF,OA=OC,推出∠EAO=∠EOA,则EA=EO=OF=FC=2,证明Rt△BFO≌Rt△BFC,得到BO=BC,易得△BOC是等边三角形,得到∠BCO=60°,∠BAC=30°,则∠FEB=2∠CAB=60°,进而推出△BEF是等边三角形,则EB=EF=4,然后根据AB=AE+EB进行计算.
9.【答案】C
【解析】【解答】解:在CD上取一点H,使,连接EH,FH,
∵四边形为正方形,
∴,
∴,即,
∵,
∴,
在和中,
,
∴,
∴,
∵,
∴,
∴,
∴是等腰直角三角形,
∴,
设,
则,
∵平分,
∴,
∴,
∵,
∴,
∵是的一个外角,
∴,
即,
∴,
∴,
∴,
∴,
即要求正方形的面积,则只需要知道的周长,
故答案为:C.
【分析】在CD上取一点H,使,先证,得出,,再证,于是得出,从而得出CD的长,即可进行判断.
10.【答案】C
【解析】【解答】连接 、 、 关于 AC 对称.
∴ .
∴ ,当 、 、 三点共线得 最小.
∴ ,选C.
【分析】连接 、 ,由于 关于 对称,可得PB=PD,由于,可得当 、 、 三点共线得 最小,最小值等于BE的长,据此解答即可.
11.【答案】12
【解析】【解答】如图,
菱形的周长为,
菱形的边长AB=,AC⊥BD,
一条对角线长,可设BD=16cm,
OB=8cm,
AC=2OA=12cm,
故答案为:12cm.
【分析】根据菱形的性质求得边长AB=10cm,OB=8cm,利用勾股定理即可求解.
12.【答案】(1,1)
【解析】【解答】解:如图,
设点C(x,y),
∵四边形AOBC是正方形,
∴BC=AC,∠B=∠A=90°,
∴BC=AC=x=y
∵点C在第一象限且在反比例函数 的图象上,
∴正方形AOBC的面积为1,即BC2=1,
∴BC=1,
∴点C(1,1).
故答案为:(1,1).
【分析】画出示意图,由正方形的性质得BC=AC,∠B=∠A=90°,由反比例函数图象k的几何意义可得正方形AOBC的面积为1,进而根据正方形的面积计算方法可求出BC的长,从而即可得出点C的坐标.
13.【答案】
【解析】【解答】解:∵正方形ABCD和正方形CEFG中,点D在CG上,BC=1,CE=3
∴AB=BC=1,CE=EF=3,∠E=90°
延长AD交EF于M,连接AC,CF
则AM=BC+CE=4,FM=EF-AB=2,∠AMF=90°
∵四边形ABCD和四边形GCEF是正方形
∵H为AF的中点
故答案为:
【分析】延长AD交EF于M,连接AC,CF,根据正方形性质及勾股定理即可求出答案.
14.【答案】
【解析】【解答】解:∵四边形是菱形,且,,
∴,
在中,,
∴菱形的周长,
故答案为:.
【分析】利用菱形的性质得到,再利用勾股定理求得,最后根据菱形的周长,从而求解.
15.【答案】
【解析】【解答】解:如图,
∵△ABC是等腰直角三角形,且AC=BC,
∴∠B=∠C=45°,
∵四边形CDHG是矩形,且CD= ,
∴HG=CD= ,∠BGH=90°,
∴∠B=∠BHG=45°,
∴GB=GH=,
∴CG=DH=BC-BG=cm,
∵四边形CDHG是矩形,
∴DH∥BC,
∴∠B=∠DHN=45°,
∵四边形DENM是矩形,且DE=,
∴MN=ED= ,∠NMH=90°,
∴∠MNH=∠MHN=45°,
∴MN=MH=,
∴DM=EN=DN-MH=cm;
同理FQ=PE=,
∵AF=AC-CD-DE-EF=,
∴这样的长方形纸条只能裁出三条,
这三条的总长度为:CG+DM+EN=cm,
∴美术作品的边长为:cm,
∴这个美术作品的面积为:cm2.
故答案为:.
【分析】由等腰直角三角形的性质得∠B=∠C=45°,由矩形的性质得HG=CD= ,∠BGH=90°,从而可推出△BHG是等腰直角三角形,得GB=GH=,CG=DH=BC-BG=cm,同理可求出DM、PE得长,可得到裁剪出的矩形纸条的总长度,进而结合图③找出美术作品的边长,最后根据正方形面积计算方法计算可得答案.
16.【答案】
【解析】【解答】解:根据题意可得:“完美菱形”的边长为,则故均为等边三角形,则又,,故在中
,则(SAS),则∵
∴则且故为等边三角形,设则的面积为则当时,x有最小值:故S的最小值为:当BM与AB重合时有最大值4,则S的最大值为则的取值范围是.
故答案为:.
【分析】本题主要考查菱形等边三角形的性质、三角形全等的证明与性质.根据题意可得:“完美菱形”的边长为,则故均为等边三角形,则然后根据已知条件结合等量代换可得:从而得到,进一步可证明为等边三角形,设则的面积为然后分当时,x有最小值和当BM与AB重合时有最大值进行求解即可.
17.【答案】证明:∵四边形ABCD是菱形,
∴∠B=∠D,AB=AD,
在△ABE和△ADF中,
,
∴△ABE≌△ADF(ASA),
∴AE=AF.
【解析】【分析】利用“ASA”证明△ABE≌△ADF,再利用全等三角形的性质可得AE=AF。
18.【答案】证明:∵ 四边形ABCD为正方形,
∴ AB=BC=BC=CD,∠ABE=∠BCF=90°,
∵ CE=DF,
∴ BC+CE=CD+DF,即BE=CF,
∴ △ABE≌△BCF(SAS),
∴ AE=BF.
【解析】【分析】根据正方形的性质得AB=BC=BC=CD,∠ABE=∠BCF=90°,推出BE=CF,依据SAS判定△ABE≌△BCF,根据全等三角形的对应边相等即可求得.
19.【答案】(1)证明:∵,
∴,
∵点E、G分别是的中点,
∴,,
∴,
∴四边形是菱形;
(2)解:∵四边形是菱形,
∴,
∵,
∴,
又∵,
∴,
∴,
∴是等边三角形,
∴,
∴.
20.【答案】(1)解:添加的条件:(答案不唯一).
证明:∵四边形ABCD为平行四边形,∴.
∵,∴四边形AECF是平行四边形(有一组对边平行且相等的四边形是平行四边形),
∴,∴.
∵,,∴,
∴四边形EGFH为矩形(有三个角是直角的四边形是矩形).
(2)解:设.∵,∴,
∴在Rt△AGF中,,∴.
∵,∴.
∵,∴,解得,∴AG的长为1.
【解析】【分析】(1)添加的条件:(答案不唯一),根据平行四边形的判定与性质证明四边形AECF是平行四边形,进而根据平行线的性质得到,再结合题意运用矩形的判定即可求解;
(2)设,先根据锐角三角函数的定义得到.进而即可得到,再结合题意即可求解。
21.【答案】(1)证明:如图,作,.
,,
四边形是正方形,
,
四边形是矩形,
,
点是正方形对角线上的点,
,
四边形是矩形,
,
,
在和中,
,
≌,
;
(2)解:四边形是矩形,,
矩形是正方形,
,,
四边形是正方形,
,,,
,
≌,
,,
,
,
,,
,
的面积
(3)解:如图,当点在线段上时,
四边形是正方形,
,
,,
;
如图,当点在线段的延长线上时,
,,
,
综上,的度数为或.
【解析】【分析】本题主要考查正方形的基本性质、矩形的判定和性质、三角形全等的判定及性质.
(1)作,,结合题意可证得四边形是矩形,然后运用矩形和正方形的性质可得到≌,进而得到答案;
(2)根据矩形和正方形的性质运用等量代换的方法可证得:≌,得到,进而表示出的面积y的表达式;
(3)分点在线段上和点在线段的延长线上两种情况进行求解即可.
22.【答案】(1)解:∵,四边形是矩形,
∴可设D坐标为,
把代入直线得:,
∴点D的坐标为,
∵经过点,
∴,解得:,
∴反比例函数的关系式为:;
(2)解:设线段,线段的长度为,
∵,
∴,
∵矩形的面积是27,
∴,解得:,
即点B,点C的横坐标为:,
把代入得:,
即点E的坐标为:,
∴线段的长度为,
∴.
【解析】【分析】(1)根据矩形的性质以及点A的坐标,可设点D坐标为,将点D坐标代入直线 ,求得的值,从而得到点D的坐标,再根据反比例函数图象上的点的坐标特征将点D的坐标代入 ,从而求解;
(2) 设线段,线段的长度为, 根据点D的坐标可得 , 由 矩形的面积是27, 得到关于m的方程,可求得m的值,从而得到点B,点C的横坐标为13,根据放比例函数图象上的点的坐标特征求得点E的坐标,进而得到线段CE的长,最后利用三角形的面积公式即可求解.
23.【答案】(1)解:45°.∵四边形ABCD是正方形,
∴AB=AD=BC=CD,∠B=∠D=∠BAD=90°,
∵AG是△AEF的高,且高AG与正方形的边长相等,
即∠AGE=∠AGF=90°,AG=AB=AD,
在Rt△ABE和Rt△AGE中,
,
∴Rt△ABE≌Rt△AGE(HL),
∴∠BAE=∠GAE;
同理,∠GAF=∠DAF;
∴.
(2)解:∵Rt△ABE≌Rt△AGE(HL),
∴BE=EG=4,
同理,DF=DG=6,
则EF=EG+FG=10,
设AB=a,则EC=a-4,CF=a-6,
在Rt△EFC中,EF2=EC2+CF2,
即102=(a-4)2+(a-6)2,
解得:a=12,
∴正方形ABCD的边长是12.
(3)解:MN2=ND2+DH2;理由如下:
如图:
则AH=AM,DH=BM,∠BAM=∠DAH,
∵∠BAD=∠MAH=90°,∠MAN=45°,
∴∠NAH=45°,
∴∠HAN=∠MAN;
在△AMN和△AHN中,
,
∴△AMN≌△AHN(SAS),
∴MN=HN,
∵∠BAD=90°,AB=AD,
∴∠ABD=∠ADB=45°,
∴∠HDN=∠HDA+∠ADB=90°,
∴NH2=ND2+DH2,
∴MN2=ND2+BM2.
【解析】【分析】(1)由正方形四条边都相等,四个角都是直角得AB=AD=BC=CD,∠B=∠D=∠BAD=90°,结合题意可得∠AGE=∠AGF=90°,AG=AB=AD,根据斜边及另一条直角边对应相等的两个直角三角形全等,全等三角形的对应角相等可得∠BAE=∠GAE,同理可得∠GAF=∠DAF,即可求解;
(2)根据全等三角形的对应边相等可得BE=EG=4,DF=DG=6,设AB=a,则EC=a-4,CF=a-6,根据直角三角形中两直角边的平方和等于斜边的平方即可求得a的值;
(3)根据旋转的对应角相等,对应边相等得AH=AM,DH=BM,∠BAM=∠DAH,得∠NAH=45°,可得∠HAN=∠MAN,根据两边和它们的夹角对应相等的两个三角形全等,全等三角形的对应边相等可得MN=HN,根据等腰直角三角形的两个底角是45°可得∠ABD=∠ADB=45°,求得∠HDN=90°,根据直角三角形中两直角边的平方和等于斜边的平方即可求解.
1 / 1
一、选择题
1.如图,四边形ABCD是平行四边形,下列说法不正确的是( )
A.当AC=BD时,四边形ABCD是矩形
B.当AB=BC时,四边形ABCD是菱形
C.当AC平分∠BAD时,四边形ABCD是菱形
D.当∠DAB= 90°时,四边形ABCD是正方形
2.菱形不具有的性质是( )
A.对角相等 B.对边平行
C.对角线互相垂直 D.对角线相等
3.关于矩形的性质、下面说法错误的是( )
A.矩形的四个角都是直角
B.矩形的两组对边分别相等
C.矩形的两组对边分别平行
D.矩形的对角线互相垂直平分且相等
4.如图,在菱形ABCD中,∠B=60°,连接AC,若AC=6,则菱形ABCD的周长为( )
A.24 B.30 C. D.
5.如图,在面积为S的菱形ABCD中,对角线AC,BD相交于点O,E,F,G分别是BC,OB,OC的中点,则四边形EFOG的面积为( )
A. B. C. D.
6.如图,已知矩形ABCD沿着直线BD折叠,使点C落在C'处,BC'交AD于E,AD=8,AB=4,则DE的长为( )
A.3 B.4 C.5 D.6
7.如图,在Rt中,4,点是斜边BC的中点,以AM为边作正方形AMEF.若S正方形AMEF=16,则( )
A. B. C.12 D.16
8.如图,在矩形 中, 、 分别是边 、 上的点, ,连接 、 , 与对角线 交于点 ,且 , , ,则 的长为( )
A. B. C.4 D.6
9.如图,在正方形中,点,分别在,上,且保持,在上取一点,连结,使恰好平分,连结.若要求正方形的面积,则只需要知道
A. 的面积 B. 的面积
C. 的周长 D. 的周长
10.如图,正方形 的面积为 , 是等边三角形,点 在正方形 内,在对角线 上有一点 ,使 的和最小,则这个最小值为( ).
A. B. C. D.
二、填空题
11.菱形的周长为,它的一条对角线长,则另一条对角线的长为 .
12.若正方形 AOBC的边OA,OB在坐标轴上,顶点 C在第一象限,且在反比例函数 的图象上,则点C的坐标是 .
13.正方形和正方形中,点在上,,,是的中点,那么的长是 .
14.如图1是清代方胜纹暗花缎袄,如图2是缎袄上面方胜纹示意图,菱形与菱形是完全相同的两个菱形,中间四边形也是菱形,、相交于点M,若,,则菱形的周长为 .
15.如图①是一张等腰直角三角形纸片,,现要求按照图②的方法裁剪几条宽度都为的长方形纸条,用这些纸条为一幅正方形美术作品EFGH镶边(纸条不重叠)如图③,正方形美术作品的面积为 .
16.如果菱形有一条对角线等于它的边长,那么称此菱形为“完美菱形”如图,已知“完美菱形”的边长为,是它的较短对角线,点、分别是边,上的两个动点,且满足,设的面积为,则的取值范围是 .
三、解答题
17.如图,点E,F分别在菱形ABCD的边BC,CD上,且∠BAE=∠DAF.求证:AE=AF.
18.如图,在正方形 ABCD中,点 E 在 BC 边的延长线上,点 F 在 CD 边的延长线上,且 CE=DF,连结 AE和BF.求证:AE=BF.
19.如图,中,,垂足为D,点E、F、G分别是中点,直线交点G.
(1)求证:四边形是菱形;
(2)若,求的度数.
20.如图,在□ABCD中,点E,F分别在边BC,AD上,连接AE,CF,过点E作于点H,过点F作于点G.
(1)请你添加一个条件: ▲,使四边形EGFH为矩形,并给出证明.
(2)在(1)的条件下,若,,,求AG的长.
21.如图,已知在正方形中,,点为线段上一点点不与、重合,连接,过点作交射线于点,以、为邻边作矩形.
(1)求证:;
(2)连接,设,的面积为求关于的函数关系式并写出自变量的取值范围;
(3)当时,求的度数.
22.如图,矩形的顶点,在轴的正半轴上,点的坐标为,点在点的右侧,反比例函数在第一象限内的图象与直线交于点,交于点.
(1)求点的坐标及反比例函数的关系式;
(2)连接,若矩形的面积是27,求出的面积.
23.【中考预测】
(1)如图1,在正方形ABCD中,△AEF的顶点E,F分别在边BC,CD上,高线AG与正方形的边长相等,求∠EAF的度数.
(2)在图1中,若EG=4,GF=6,求正方形ABCD的边长.
(3)如图2,在Rt△ABD中,AD,M,N是边BD上的任意两点,且∠MAN=45°,将△ABM绕点A逆时针旋转90°至△ADH的位置,连结NH,试判断MN ,ND ,DH 之间的数量关系,并说明理由.
答案解析部分
1.【答案】D
【解析】【解答】解:①对角线相等的平行四边形是矩形,故A正确;
②有一组邻边相等的平行四边形是菱形,故B正确;
③∵AC平分∠BAD,
∴∠DAC=∠CAB,
∵CD∥AB,
∴∠DCA=∠CAB,
∴∠DAC=∠DCA,
∴DA=DC,
∴平行四边形ABCD是菱形,故C正确;
④当∠DAB=90°,平行四边形ABCD是矩形,不能判定其是正方形,故D错误;
故答案为:D.
【分析】通过矩形、菱形、矩形及正方形的判定方法一 一判断即可.
2.【答案】D
【解析】【解答】解:A、菱形是特殊的平行四边形,其对角是相等的,故此选项不符合题意;
B、菱形是特殊的平行四边形,其对边是互相平行的,故此选项不符合题意;
C、菱形的对角线互相垂直且平分,每一条对角线平分一组对角,故此选项不符合题意;
D、菱形的对角线只是互相垂直且平分,每一条对角线平分一组对角,不一定相等,故此选项符合题意.
故答案为:D.
【分析】菱形是特殊的平行四边形,具有对角相等、对边平行、四条边相等、对角线互相垂直且平分,每一条对角线平分一组对角,据此逐项判断即可得解.
3.【答案】D
【解析】【解答】A、∵矩形的四个角都是直角,∴A正确,不符合题意;
B、∵矩形的两组对边分别相等,∴B正确,不符合题意;
C、∵矩形的两组对边分别平行,∴C正确,不符合题意;
D、∵矩形的对角线互相平分且相等但不垂直,∴D不正确,符合题意;
故答案为:D.
【分析】利用矩形的性质逐项分析判断即可.
4.【答案】A
【解析】【解答】解:∵四边形ABCD是菱形,
∴AB=BC=CD=AD.
∵∠B=60°,
∴△ABC是等边三角形.
∴AB=AC=6,
故菱形的周长是4×6=24.
故答案为:A.
【分析】根据菱形的性质和∠B的度数判断△ABC是等边三角形,从而得到AB=AC=6,于是可得周长.
5.【答案】B
【解析】【解答】解:如图所示,连接OE,
∵四边形ABCD是菱形,
∴∠BOC=90°,
又∵E是BC的中点,
∴OE=BE=CE,
又∵F,G分别是BO,CO的中点,
∴EF⊥OB,EG⊥OC,
∴四边形OGEF是矩形,
∵菱形ABCD的面积为S,
∴AC×BD=S,即AC×BD=2S,
∴四边形EFOG的面积=OG×OF=OC×OB=AC×BD=AC×BD=×2S=S.
故答案为:B.
【分析】连接OE,根据菱形的性质及等腰三角形的性质,即可得出EF⊥OB,EG⊥OC,推出四边形OGEF是矩形,再根据菱形的面积即可得出矩形的面积。
6.【答案】C
【解析】【解答】解:∵四边形ABCD是矩形,
∴AB=CD,∠C=∠A=90°
由折叠的性质可得:C'D=CD=AB;∠C'=∠C=∠A
在△ABE与△C'ED中
∴△ABE≌△C'ED(AAS)
∴DE=BE
设DE=BE=x,则AE=8-x,AB=4,在直角三角形ABE中,
解得x=5
故答案为:C.
【分析】由矩形性质得AB=CD,∠C=∠A=90°,利用折叠的性质得C'D=CD=AB,∠C'=∠C=∠A;再利用AAS证明△ABE≌△C'ED,利用全等三角形的对应边相等,可证得DE=BE,设DE=BE=x,可表示出AE的长,然后利用勾股定理建立关于x的方程,解方程求出x的值.
7.【答案】B
【解析】【解答】解:∵四边形AMEF是正方形,S正方形AMEF=16,
∴AM2=16,
∴AM=4,
在Rt△ABC中,点M是斜边BC的中点,
∴,
即BC=2AM=8,
在Rt△ABC中,AB=4,
∴,
∴,
故答案为:B.
【分析】先根据正方形AMEF的面积求出AM的长,然后根据直角三角形斜边上的中线等于斜边的一半求出BC的长,在Rt△ABC中通过勾股定理求出AC的长,最后利用直角三角形的面积公式可求出△ABC的面积即可解答.
8.【答案】D
【解析】【解答】解:如图,连接BO,
∵四边形ABCD是矩形,
∴DC∥AB,∠DCB=90°
∴∠FCO=∠EAO,
在△AOE和△COF中,
,
∴△AOE≌△COF,
∴OE=OF,OA=OC,
∵BF=BE,
∴BO⊥EF,∠BOF=90°,
∵∠FEB=2∠CAB=∠CAB+∠AOE,
∴∠EAO=∠EOA,
∴EA=EO=OF=FC=2,
在Rt△BFO和Rt△BFC中,
,
∴Rt△BFO≌Rt△BFC,
∴BO=BC,
在Rt△ABC中,∵AO=OC,
∴BO=AO=OC=BC,
∴△BOC是等边三角形,
∴∠BCO=60°,∠BAC=30°,
∴∠FEB=2∠CAB=60°,
∵BE=BF,
∴△BEF是等边三角形,
∴EB=EF=4,
∴AB=AE+EB=2+4=6.
故答案为:D.
【分析】连接BO,根据矩形的性质可得DC∥AB,∠DCB=90°,根据平行线的性质可得∠FCO=∠EAO,证明△AOE≌△COF,得到OE=OF,OA=OC,推出∠EAO=∠EOA,则EA=EO=OF=FC=2,证明Rt△BFO≌Rt△BFC,得到BO=BC,易得△BOC是等边三角形,得到∠BCO=60°,∠BAC=30°,则∠FEB=2∠CAB=60°,进而推出△BEF是等边三角形,则EB=EF=4,然后根据AB=AE+EB进行计算.
9.【答案】C
【解析】【解答】解:在CD上取一点H,使,连接EH,FH,
∵四边形为正方形,
∴,
∴,即,
∵,
∴,
在和中,
,
∴,
∴,
∵,
∴,
∴,
∴是等腰直角三角形,
∴,
设,
则,
∵平分,
∴,
∴,
∵,
∴,
∵是的一个外角,
∴,
即,
∴,
∴,
∴,
∴,
即要求正方形的面积,则只需要知道的周长,
故答案为:C.
【分析】在CD上取一点H,使,先证,得出,,再证,于是得出,从而得出CD的长,即可进行判断.
10.【答案】C
【解析】【解答】连接 、 、 关于 AC 对称.
∴ .
∴ ,当 、 、 三点共线得 最小.
∴ ,选C.
【分析】连接 、 ,由于 关于 对称,可得PB=PD,由于,可得当 、 、 三点共线得 最小,最小值等于BE的长,据此解答即可.
11.【答案】12
【解析】【解答】如图,
菱形的周长为,
菱形的边长AB=,AC⊥BD,
一条对角线长,可设BD=16cm,
OB=8cm,
AC=2OA=12cm,
故答案为:12cm.
【分析】根据菱形的性质求得边长AB=10cm,OB=8cm,利用勾股定理即可求解.
12.【答案】(1,1)
【解析】【解答】解:如图,
设点C(x,y),
∵四边形AOBC是正方形,
∴BC=AC,∠B=∠A=90°,
∴BC=AC=x=y
∵点C在第一象限且在反比例函数 的图象上,
∴正方形AOBC的面积为1,即BC2=1,
∴BC=1,
∴点C(1,1).
故答案为:(1,1).
【分析】画出示意图,由正方形的性质得BC=AC,∠B=∠A=90°,由反比例函数图象k的几何意义可得正方形AOBC的面积为1,进而根据正方形的面积计算方法可求出BC的长,从而即可得出点C的坐标.
13.【答案】
【解析】【解答】解:∵正方形ABCD和正方形CEFG中,点D在CG上,BC=1,CE=3
∴AB=BC=1,CE=EF=3,∠E=90°
延长AD交EF于M,连接AC,CF
则AM=BC+CE=4,FM=EF-AB=2,∠AMF=90°
∵四边形ABCD和四边形GCEF是正方形
∵H为AF的中点
故答案为:
【分析】延长AD交EF于M,连接AC,CF,根据正方形性质及勾股定理即可求出答案.
14.【答案】
【解析】【解答】解:∵四边形是菱形,且,,
∴,
在中,,
∴菱形的周长,
故答案为:.
【分析】利用菱形的性质得到,再利用勾股定理求得,最后根据菱形的周长,从而求解.
15.【答案】
【解析】【解答】解:如图,
∵△ABC是等腰直角三角形,且AC=BC,
∴∠B=∠C=45°,
∵四边形CDHG是矩形,且CD= ,
∴HG=CD= ,∠BGH=90°,
∴∠B=∠BHG=45°,
∴GB=GH=,
∴CG=DH=BC-BG=cm,
∵四边形CDHG是矩形,
∴DH∥BC,
∴∠B=∠DHN=45°,
∵四边形DENM是矩形,且DE=,
∴MN=ED= ,∠NMH=90°,
∴∠MNH=∠MHN=45°,
∴MN=MH=,
∴DM=EN=DN-MH=cm;
同理FQ=PE=,
∵AF=AC-CD-DE-EF=,
∴这样的长方形纸条只能裁出三条,
这三条的总长度为:CG+DM+EN=cm,
∴美术作品的边长为:cm,
∴这个美术作品的面积为:cm2.
故答案为:.
【分析】由等腰直角三角形的性质得∠B=∠C=45°,由矩形的性质得HG=CD= ,∠BGH=90°,从而可推出△BHG是等腰直角三角形,得GB=GH=,CG=DH=BC-BG=cm,同理可求出DM、PE得长,可得到裁剪出的矩形纸条的总长度,进而结合图③找出美术作品的边长,最后根据正方形面积计算方法计算可得答案.
16.【答案】
【解析】【解答】解:根据题意可得:“完美菱形”的边长为,则故均为等边三角形,则又,,故在中
,则(SAS),则∵
∴则且故为等边三角形,设则的面积为则当时,x有最小值:故S的最小值为:当BM与AB重合时有最大值4,则S的最大值为则的取值范围是.
故答案为:.
【分析】本题主要考查菱形等边三角形的性质、三角形全等的证明与性质.根据题意可得:“完美菱形”的边长为,则故均为等边三角形,则然后根据已知条件结合等量代换可得:从而得到,进一步可证明为等边三角形,设则的面积为然后分当时,x有最小值和当BM与AB重合时有最大值进行求解即可.
17.【答案】证明:∵四边形ABCD是菱形,
∴∠B=∠D,AB=AD,
在△ABE和△ADF中,
,
∴△ABE≌△ADF(ASA),
∴AE=AF.
【解析】【分析】利用“ASA”证明△ABE≌△ADF,再利用全等三角形的性质可得AE=AF。
18.【答案】证明:∵ 四边形ABCD为正方形,
∴ AB=BC=BC=CD,∠ABE=∠BCF=90°,
∵ CE=DF,
∴ BC+CE=CD+DF,即BE=CF,
∴ △ABE≌△BCF(SAS),
∴ AE=BF.
【解析】【分析】根据正方形的性质得AB=BC=BC=CD,∠ABE=∠BCF=90°,推出BE=CF,依据SAS判定△ABE≌△BCF,根据全等三角形的对应边相等即可求得.
19.【答案】(1)证明:∵,
∴,
∵点E、G分别是的中点,
∴,,
∴,
∴四边形是菱形;
(2)解:∵四边形是菱形,
∴,
∵,
∴,
又∵,
∴,
∴,
∴是等边三角形,
∴,
∴.
20.【答案】(1)解:添加的条件:(答案不唯一).
证明:∵四边形ABCD为平行四边形,∴.
∵,∴四边形AECF是平行四边形(有一组对边平行且相等的四边形是平行四边形),
∴,∴.
∵,,∴,
∴四边形EGFH为矩形(有三个角是直角的四边形是矩形).
(2)解:设.∵,∴,
∴在Rt△AGF中,,∴.
∵,∴.
∵,∴,解得,∴AG的长为1.
【解析】【分析】(1)添加的条件:(答案不唯一),根据平行四边形的判定与性质证明四边形AECF是平行四边形,进而根据平行线的性质得到,再结合题意运用矩形的判定即可求解;
(2)设,先根据锐角三角函数的定义得到.进而即可得到,再结合题意即可求解。
21.【答案】(1)证明:如图,作,.
,,
四边形是正方形,
,
四边形是矩形,
,
点是正方形对角线上的点,
,
四边形是矩形,
,
,
在和中,
,
≌,
;
(2)解:四边形是矩形,,
矩形是正方形,
,,
四边形是正方形,
,,,
,
≌,
,,
,
,
,,
,
的面积
(3)解:如图,当点在线段上时,
四边形是正方形,
,
,,
;
如图,当点在线段的延长线上时,
,,
,
综上,的度数为或.
【解析】【分析】本题主要考查正方形的基本性质、矩形的判定和性质、三角形全等的判定及性质.
(1)作,,结合题意可证得四边形是矩形,然后运用矩形和正方形的性质可得到≌,进而得到答案;
(2)根据矩形和正方形的性质运用等量代换的方法可证得:≌,得到,进而表示出的面积y的表达式;
(3)分点在线段上和点在线段的延长线上两种情况进行求解即可.
22.【答案】(1)解:∵,四边形是矩形,
∴可设D坐标为,
把代入直线得:,
∴点D的坐标为,
∵经过点,
∴,解得:,
∴反比例函数的关系式为:;
(2)解:设线段,线段的长度为,
∵,
∴,
∵矩形的面积是27,
∴,解得:,
即点B,点C的横坐标为:,
把代入得:,
即点E的坐标为:,
∴线段的长度为,
∴.
【解析】【分析】(1)根据矩形的性质以及点A的坐标,可设点D坐标为,将点D坐标代入直线 ,求得的值,从而得到点D的坐标,再根据反比例函数图象上的点的坐标特征将点D的坐标代入 ,从而求解;
(2) 设线段,线段的长度为, 根据点D的坐标可得 , 由 矩形的面积是27, 得到关于m的方程,可求得m的值,从而得到点B,点C的横坐标为13,根据放比例函数图象上的点的坐标特征求得点E的坐标,进而得到线段CE的长,最后利用三角形的面积公式即可求解.
23.【答案】(1)解:45°.∵四边形ABCD是正方形,
∴AB=AD=BC=CD,∠B=∠D=∠BAD=90°,
∵AG是△AEF的高,且高AG与正方形的边长相等,
即∠AGE=∠AGF=90°,AG=AB=AD,
在Rt△ABE和Rt△AGE中,
,
∴Rt△ABE≌Rt△AGE(HL),
∴∠BAE=∠GAE;
同理,∠GAF=∠DAF;
∴.
(2)解:∵Rt△ABE≌Rt△AGE(HL),
∴BE=EG=4,
同理,DF=DG=6,
则EF=EG+FG=10,
设AB=a,则EC=a-4,CF=a-6,
在Rt△EFC中,EF2=EC2+CF2,
即102=(a-4)2+(a-6)2,
解得:a=12,
∴正方形ABCD的边长是12.
(3)解:MN2=ND2+DH2;理由如下:
如图:
则AH=AM,DH=BM,∠BAM=∠DAH,
∵∠BAD=∠MAH=90°,∠MAN=45°,
∴∠NAH=45°,
∴∠HAN=∠MAN;
在△AMN和△AHN中,
,
∴△AMN≌△AHN(SAS),
∴MN=HN,
∵∠BAD=90°,AB=AD,
∴∠ABD=∠ADB=45°,
∴∠HDN=∠HDA+∠ADB=90°,
∴NH2=ND2+DH2,
∴MN2=ND2+BM2.
【解析】【分析】(1)由正方形四条边都相等,四个角都是直角得AB=AD=BC=CD,∠B=∠D=∠BAD=90°,结合题意可得∠AGE=∠AGF=90°,AG=AB=AD,根据斜边及另一条直角边对应相等的两个直角三角形全等,全等三角形的对应角相等可得∠BAE=∠GAE,同理可得∠GAF=∠DAF,即可求解;
(2)根据全等三角形的对应边相等可得BE=EG=4,DF=DG=6,设AB=a,则EC=a-4,CF=a-6,根据直角三角形中两直角边的平方和等于斜边的平方即可求得a的值;
(3)根据旋转的对应角相等,对应边相等得AH=AM,DH=BM,∠BAM=∠DAH,得∠NAH=45°,可得∠HAN=∠MAN,根据两边和它们的夹角对应相等的两个三角形全等,全等三角形的对应边相等可得MN=HN,根据等腰直角三角形的两个底角是45°可得∠ABD=∠ADB=45°,求得∠HDN=90°,根据直角三角形中两直角边的平方和等于斜边的平方即可求解.
1 / 1
