青岛版五年级上册数学方程应用复习(课件)(共18张PPT)
文档属性
| 名称 | 青岛版五年级上册数学方程应用复习(课件)(共18张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 151.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-24 00:00:00 | ||
图片预览





文档简介
(共18张PPT)
方程应用 复习
知识重点
回顾与思考
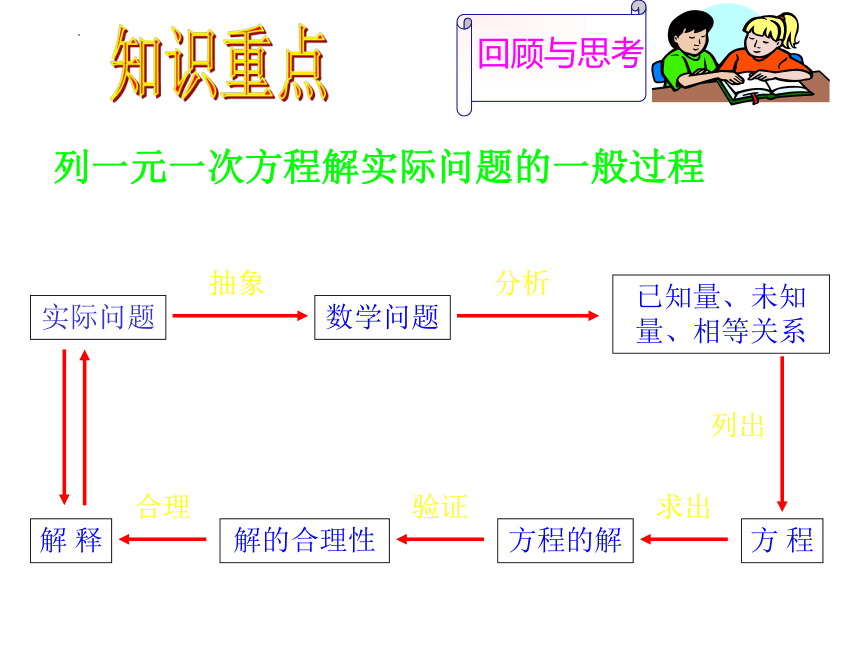
列一元一次方程解实际问题的一般过程
实际问题
数学问题
已知量、未知量、相等关系
解释
解的合理性
方程的解
方程
抽象
分析
合理
验证
求出
列出
回顾与思考
列一元一次方程解实际问题的一般步骤
1、审:审题,分析题中已知什么、求什么、明确各 数量之间的关系
2、设:设未知数(直接设法、间接设法)
3、找:找出能够表示题中全部含义的一个等量关系
4、列:根据等量关系列出方程
5、解:解所列出的方程,求出未知数的值
6、答:检验所求的解是否符合题意,在写出答案
知识重点
回顾与思考
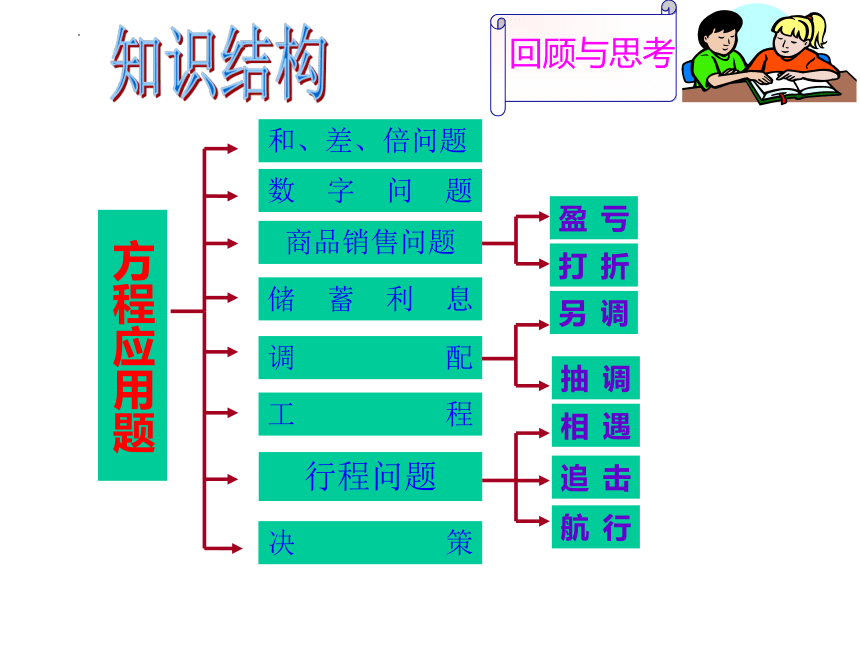
知识结构
方程应用题
工程
储蓄利息
商品销售问题
调配
决策
数字问题
行程问题
航行
和、差、倍问题
追击
另调
抽调
相遇
盈亏
打折
设未知数的技巧:
1、设直接未知数,即求什么设什么。
2、设间接未知数。
3、设辅助未知数,即“设而不求”
在列方程解决实际问题的过程应注意哪些问题?
(1)设未知数时,要仔细分析问题中的数量关系,找出题中的已知条件和未知数,一般采用直接设法,有些问题可用间接设法,要注意未知数的单位,不要漏写。
(2)找等量关系时,可借助图表分析题中的数量关系, 列出两个代数式,使它们都表示一个相等或相同的量。
(3)列方程时,要注意方程各项是同类
量,单位要一致,方程左右两边应是等
量。
(4)解出方程的解后,要验证它的合理
性,再解释它的意义,并要注意单位。
(5)在解决实际问题的过程中,你是怎样判断一个方程的解是否合理?请举例说明。
找规律解方程应用题
一、日历中的方程
例1 如图某月日历,如果用正方形所圈出4个数的和是76 ,这4天分别是几号?
日 一 二 三 四 五 六
1 2 3 4 5 6
7 8 9 10 11 12 13
14 15 16 17 18 19 20
21 22 23 24 25 26 27
28 29 30
问题:日历中阴影中的9个数的和能等于136吗?
如下图,将一张正方形纸片,剪成四个大小形状一样的小正方形,然后将其中的一个小正方形再按同样的方法剪成四个小正方形,再将其中的一个小正方形剪成四个小正方形,如此循环进行下去;
(1)填表:
剪的次数
1
2
3
4
5
正方形
个数
(2)如果剪n次,共剪出多少个小正方形?
(3)如果共剪出301个小正方形,则剪了
几 次?
4 7 10 13 16
有一些分别标有6,12,18,24,30,36,…..的卡片,小明从中任意拿到了相邻的3张卡片,发现这些卡片上的数字的和为342
猜猜小明拿到了哪3张卡片?
小明能否拿到相邻的3张卡片,使得它们的和为86?说明理由?
6个人围成一圈,每人心里想一个数,并把这个数告诉左、右两个人,然后每一个人把左、右两个相邻人告诉自己的数的平均数亮出来,如图,问亮出11的人原来心中想的那个数是多少?
如图:一个长方形被划分成6个正方形,已知中间的最小的正方形面积为1平方厘米,求这个正方形的面积
如图:某一地区的自来水网络,小圆圈表示粗细不同的水管相连通,连线管标注的数字表示该段水管单位时间内可以通过的最大流水量,现从A向连接点B输送自来水,自来水可以沿不同路线输送,则单位时间内输送水量最大的是( )
(A)19 (B)24 (c)25 (D)26
你喜欢吃拉面吗?拉面馆的师傅,用一根很粗的面条,
把两头捏合在一起拉伸,再捏合,再拉伸,反复几次,就把这根很粗的面条拉成了许多细的面条,如下图所示:
第一次捏合 第二次捏合 第三次捏合
(1)这样捏合4次后可拉出多少根面条?5次呢?n次呢?
(2)捏合多少次后可拉出64根面条?
如下图所示,由一些点组成形如三角形的图形,每条边
(包括两个顶点)有n (n>1)个点,每个图形总的点数s是
多少?当n=7,11时,s是多少?你会列式计算吗
n=2 n=3 n=4 n=5
s= s= s= s=
3 6 9 12
这时s又分别是多少呢?
黑蚂蚁和红蚂蚁都认为自己跑得比对方快,刚好它们看到地上的几个半圆(图1),于是它们决定比一比。黑蚂蚁沿着大半圆从甲处跑到乙处;红蚂蚁沿着两个小半圆也从甲处跑到乙处。两只蚂蚁同时起跑,
(1) 两只蚂蚁请你帮助判断:谁跑得快?
(2)两只蚂蚁对你的判断结果很不满意,决定再到(图2)的几个半圆处再比赛一次,请你猜一猜,哪一只蚂蚁先从甲处跑到乙处?
思考
在快乐学习中健康成长,
在健康成长中快乐学习。
教 师 寄 语
方程的思想很重要,但我们现在所学的一元一次方程只是窥见方程这座巨大的冰山的一角,在以后我们还会接触到方程的奇妙之处.
方程应用 复习
知识重点
回顾与思考
列一元一次方程解实际问题的一般过程
实际问题
数学问题
已知量、未知量、相等关系
解释
解的合理性
方程的解
方程
抽象
分析
合理
验证
求出
列出
回顾与思考
列一元一次方程解实际问题的一般步骤
1、审:审题,分析题中已知什么、求什么、明确各 数量之间的关系
2、设:设未知数(直接设法、间接设法)
3、找:找出能够表示题中全部含义的一个等量关系
4、列:根据等量关系列出方程
5、解:解所列出的方程,求出未知数的值
6、答:检验所求的解是否符合题意,在写出答案
知识重点
回顾与思考
知识结构
方程应用题
工程
储蓄利息
商品销售问题
调配
决策
数字问题
行程问题
航行
和、差、倍问题
追击
另调
抽调
相遇
盈亏
打折
设未知数的技巧:
1、设直接未知数,即求什么设什么。
2、设间接未知数。
3、设辅助未知数,即“设而不求”
在列方程解决实际问题的过程应注意哪些问题?
(1)设未知数时,要仔细分析问题中的数量关系,找出题中的已知条件和未知数,一般采用直接设法,有些问题可用间接设法,要注意未知数的单位,不要漏写。
(2)找等量关系时,可借助图表分析题中的数量关系, 列出两个代数式,使它们都表示一个相等或相同的量。
(3)列方程时,要注意方程各项是同类
量,单位要一致,方程左右两边应是等
量。
(4)解出方程的解后,要验证它的合理
性,再解释它的意义,并要注意单位。
(5)在解决实际问题的过程中,你是怎样判断一个方程的解是否合理?请举例说明。
找规律解方程应用题
一、日历中的方程
例1 如图某月日历,如果用正方形所圈出4个数的和是76 ,这4天分别是几号?
日 一 二 三 四 五 六
1 2 3 4 5 6
7 8 9 10 11 12 13
14 15 16 17 18 19 20
21 22 23 24 25 26 27
28 29 30
问题:日历中阴影中的9个数的和能等于136吗?
如下图,将一张正方形纸片,剪成四个大小形状一样的小正方形,然后将其中的一个小正方形再按同样的方法剪成四个小正方形,再将其中的一个小正方形剪成四个小正方形,如此循环进行下去;
(1)填表:
剪的次数
1
2
3
4
5
正方形
个数
(2)如果剪n次,共剪出多少个小正方形?
(3)如果共剪出301个小正方形,则剪了
几 次?
4 7 10 13 16
有一些分别标有6,12,18,24,30,36,…..的卡片,小明从中任意拿到了相邻的3张卡片,发现这些卡片上的数字的和为342
猜猜小明拿到了哪3张卡片?
小明能否拿到相邻的3张卡片,使得它们的和为86?说明理由?
6个人围成一圈,每人心里想一个数,并把这个数告诉左、右两个人,然后每一个人把左、右两个相邻人告诉自己的数的平均数亮出来,如图,问亮出11的人原来心中想的那个数是多少?
如图:一个长方形被划分成6个正方形,已知中间的最小的正方形面积为1平方厘米,求这个正方形的面积
如图:某一地区的自来水网络,小圆圈表示粗细不同的水管相连通,连线管标注的数字表示该段水管单位时间内可以通过的最大流水量,现从A向连接点B输送自来水,自来水可以沿不同路线输送,则单位时间内输送水量最大的是( )
(A)19 (B)24 (c)25 (D)26
你喜欢吃拉面吗?拉面馆的师傅,用一根很粗的面条,
把两头捏合在一起拉伸,再捏合,再拉伸,反复几次,就把这根很粗的面条拉成了许多细的面条,如下图所示:
第一次捏合 第二次捏合 第三次捏合
(1)这样捏合4次后可拉出多少根面条?5次呢?n次呢?
(2)捏合多少次后可拉出64根面条?
如下图所示,由一些点组成形如三角形的图形,每条边
(包括两个顶点)有n (n>1)个点,每个图形总的点数s是
多少?当n=7,11时,s是多少?你会列式计算吗
n=2 n=3 n=4 n=5
s= s= s= s=
3 6 9 12
这时s又分别是多少呢?
黑蚂蚁和红蚂蚁都认为自己跑得比对方快,刚好它们看到地上的几个半圆(图1),于是它们决定比一比。黑蚂蚁沿着大半圆从甲处跑到乙处;红蚂蚁沿着两个小半圆也从甲处跑到乙处。两只蚂蚁同时起跑,
(1) 两只蚂蚁请你帮助判断:谁跑得快?
(2)两只蚂蚁对你的判断结果很不满意,决定再到(图2)的几个半圆处再比赛一次,请你猜一猜,哪一只蚂蚁先从甲处跑到乙处?
思考
在快乐学习中健康成长,
在健康成长中快乐学习。
教 师 寄 语
方程的思想很重要,但我们现在所学的一元一次方程只是窥见方程这座巨大的冰山的一角,在以后我们还会接触到方程的奇妙之处.
