人教版六年级数学下册6.1.2数的认识课件(共22张PPT)
文档属性
| 名称 | 人教版六年级数学下册6.1.2数的认识课件(共22张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-24 13:25:38 | ||
图片预览








文档简介
(共22张PPT)
六年级下册
数的认识(2)
1.数与代数
情境导入
某小学有一位张老师,请你猜一猜张老师今年多少岁。
张老师
提示:张老师年龄的十位上的数字是3的最大因数也是它最小的倍数,个位上的数字是最小的质数。
回顾整理
1.你能根据a÷b=c(a、b、c均为整数,且 b≠0)说明因数与倍数的含义吗?
【教材P72 第4题】
15÷3=5,3和5是15的因数,15是3和5的倍数。
b和c都是a的因数,a是b和c的倍数。
因数和倍数是相互依存的。
一个数的倍数有什么特征?你想到哪些数的倍数的特征?
一个数的倍数的个数是无限的,最小的倍数是它本身 ,没有最大的倍数。
2的倍数特征是:个位上是0,2,4,6或8
5的倍数特征是:个位上是0或5
3的倍数特征是:各个数位上的数字之和是3的倍数
什么是偶数?偶数的个位有什么特征?什么是奇数?奇数的个位有什么特征?
能被2整除的数是偶数,其个位上是0、2、4、6、8;不能被2整除的数是奇数,其个位上是1、3、5、7、9。
2的倍数特征
偶数
奇数
一个数的因数有什么特征?你想到哪些数的因数的特征?
一个数的因数的个数是有限的,最小的因数是1 ,最大的因数是它本身。
质数只有1和它本身两个因数。
合数有两个以上的因数。
1既不是质数也不是合数。
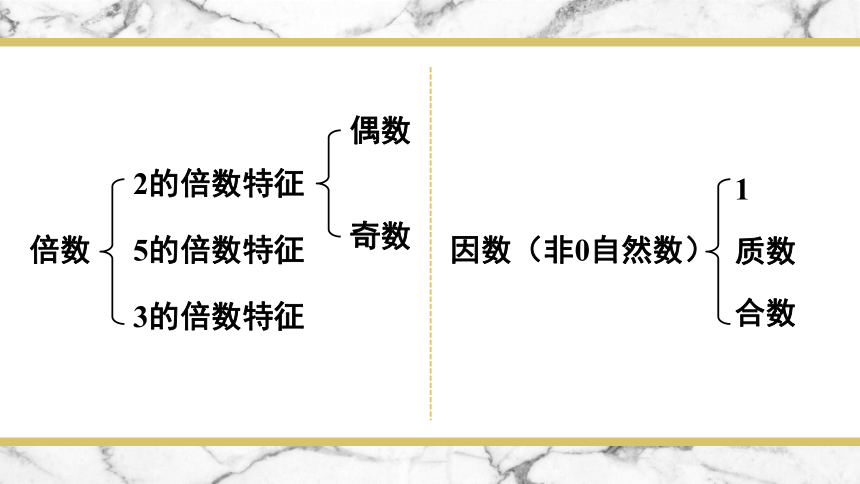
倍数
2的倍数特征
5的倍数特征
3的倍数特征
偶数
奇数
因数(非0自然数)
1
质数
合数
请你在1~20的自然数中,选择合适的数填入圈内。
质数
合数
偶数
奇数
既是质数又是偶数
既是合数又是奇数
2,3,5,7,11,
13,17,19
4,6,8,9,10,12,
14,15,16,18,20
2,4,6,8,10,12,
14,16,18,20
1,3,5,7,9,11,
13,15,17,19
2
9,15
写出36和54的公因数、最大公因数、公倍数和最小公倍数。
36的因数:1, 2, 3, 4, 6, 9, 12, 18, 36
54的因数:1, 2, 3, 6, 9, 18, 27, 54
1 2 3 6 9 18
1 2 3 6 9 18
36、54的最大公因数是18。
36的倍数:36, 72, 108, 144, 180, 216……
54的倍数:54, 108, 162, 216, 270, 324……
108 216
108 216
36、54的最小公倍数是108。
如果a÷b=c(a、b、c均为正整数),那么a和b的最大公因数是什么?最小公倍数是什么?
“六一”儿童节,张老师买来苹果64个,水果糖96颗,平均分给全班同学,都刚好分完。你知道这个班最多有多少人吗?
64 96
2
32 48
2
16 24
2
8 12
2
4 6
2
2 3
求64和96的最大公因数。
64和96的最大公因数是:
2×2×2×2×2=32
答:这个班最多有32人。
一箱苹果,如果每8个装一盒,还剩余6个;如果每10个装一盒,也剩余6个。这箱苹果至少有多少个?
【教材P74 练习十四 第9*题】
分析:根据题意可知,这箱苹果的个数减去6的差正好是8和10的公倍数。
8=2×2×2 10=2×5
8和10的最小公倍数是2×2×2×5=40,40+6=46(个)。
答:这箱苹果至少有46个。
随堂练习
1.判断下面的说法是否正确,并说一说你的理由。
(1)把0.56扩大到它的100倍是560。
(2)0是正数。
(3)假分数的倒数一定都是真分数。
(4)所有的偶数都是合数。
(5)a(a为整数,a>1)的所有因数都小于a。
【教材P74 练习十四 第6题】
×
56
×
0既不是正数,也不是负数
×
分子、分母相同的假分数的倒数依然是假分数
×
2是质数
×
a的因数还包括它本身
2.数字2、3、4、5能组成多少个没有重复数字的两位数?
(1)这些两位数中,哪些是奇数?哪些是偶数?
【教材P74 练习十四 第5题】
23,24,25,32,34,35,42,43,45,52,53,54,共12个
奇数:23,25,35,43,45,53
偶数:24,32,34,42,52,54
2.数字2、3、4、5能组成多少个没有重复数字的两位数?
(2)这些两位数中,哪些是质数?哪些是合数?
【教材P74 练习十四 第5题】
23,24,25,32,34,35,42,43,45,52,53,54,共12个
质数:23,43,53
合数:24,25,32,34,35,42,45,52,54
2.数字2、3、4、5能组成多少个没有重复数字的两位数?
(3)这些两位数中,哪些是2的倍数?哪些是3的倍数?哪些是5的倍数?
【教材P74 练习十四 第5题】
23,24,25,32,34,35,42,43,45,52,53,54,共12个
2的倍数:24,32,34,42,52,54
3的倍数:24,42,45,54
5的倍数:25,35,45
2.数字2、3、4、5能组成多少个没有重复数字的两位数?
(4)这些两位数中,2和3的公倍数有___________,3
和5的公倍数是______。
【教材P74 练习十四 第5题】
23,24,25,32,34,35,42,43,45,52,53,54,共12个
24,42,54
45
3.找规律,填数。
(1)0.9,0.99,0.999,0.9999,( ),…,这列数越来越大,越来越接近( )。
(2) , , , , ,( ),…,这列数越来越小,越来越接近( )。
【教材P74 练习十四 第7题】
0.99999
1
0
4.比较 、 、 、 的大小。你能发现什么?根据你发现的规律猜一下 与 哪个更大,并设法验证。
【教材P74 练习十四 第8题】
发现:分母与分子的差相等的真分数相比较,分母越大这个分数就越大。
猜想:
证明:
因为 ,所以 。
课堂小结
倍数
2的倍数特征
5的倍数特征
3的倍数特征
偶数
奇数
因数(非0自然数)
1
质数
合数
一、判断。(对的画“√”,错的画“×”)
20÷4=5,那么4叫因数,20叫倍数。 ( )
两个质数一定是互质数,两个合数一定不是互质数。
( )
×
×
巩固练习
三个连续自然数的和一定是6的倍数。 ( )
×
4.所有偶数(0除外)的最大公因数是2。
( )
5.两个不同数的最小公倍数一定大于最大公因数。
( )
√
√
六年级下册
数的认识(2)
1.数与代数
情境导入
某小学有一位张老师,请你猜一猜张老师今年多少岁。
张老师
提示:张老师年龄的十位上的数字是3的最大因数也是它最小的倍数,个位上的数字是最小的质数。
回顾整理
1.你能根据a÷b=c(a、b、c均为整数,且 b≠0)说明因数与倍数的含义吗?
【教材P72 第4题】
15÷3=5,3和5是15的因数,15是3和5的倍数。
b和c都是a的因数,a是b和c的倍数。
因数和倍数是相互依存的。
一个数的倍数有什么特征?你想到哪些数的倍数的特征?
一个数的倍数的个数是无限的,最小的倍数是它本身 ,没有最大的倍数。
2的倍数特征是:个位上是0,2,4,6或8
5的倍数特征是:个位上是0或5
3的倍数特征是:各个数位上的数字之和是3的倍数
什么是偶数?偶数的个位有什么特征?什么是奇数?奇数的个位有什么特征?
能被2整除的数是偶数,其个位上是0、2、4、6、8;不能被2整除的数是奇数,其个位上是1、3、5、7、9。
2的倍数特征
偶数
奇数
一个数的因数有什么特征?你想到哪些数的因数的特征?
一个数的因数的个数是有限的,最小的因数是1 ,最大的因数是它本身。
质数只有1和它本身两个因数。
合数有两个以上的因数。
1既不是质数也不是合数。
倍数
2的倍数特征
5的倍数特征
3的倍数特征
偶数
奇数
因数(非0自然数)
1
质数
合数
请你在1~20的自然数中,选择合适的数填入圈内。
质数
合数
偶数
奇数
既是质数又是偶数
既是合数又是奇数
2,3,5,7,11,
13,17,19
4,6,8,9,10,12,
14,15,16,18,20
2,4,6,8,10,12,
14,16,18,20
1,3,5,7,9,11,
13,15,17,19
2
9,15
写出36和54的公因数、最大公因数、公倍数和最小公倍数。
36的因数:1, 2, 3, 4, 6, 9, 12, 18, 36
54的因数:1, 2, 3, 6, 9, 18, 27, 54
1 2 3 6 9 18
1 2 3 6 9 18
36、54的最大公因数是18。
36的倍数:36, 72, 108, 144, 180, 216……
54的倍数:54, 108, 162, 216, 270, 324……
108 216
108 216
36、54的最小公倍数是108。
如果a÷b=c(a、b、c均为正整数),那么a和b的最大公因数是什么?最小公倍数是什么?
“六一”儿童节,张老师买来苹果64个,水果糖96颗,平均分给全班同学,都刚好分完。你知道这个班最多有多少人吗?
64 96
2
32 48
2
16 24
2
8 12
2
4 6
2
2 3
求64和96的最大公因数。
64和96的最大公因数是:
2×2×2×2×2=32
答:这个班最多有32人。
一箱苹果,如果每8个装一盒,还剩余6个;如果每10个装一盒,也剩余6个。这箱苹果至少有多少个?
【教材P74 练习十四 第9*题】
分析:根据题意可知,这箱苹果的个数减去6的差正好是8和10的公倍数。
8=2×2×2 10=2×5
8和10的最小公倍数是2×2×2×5=40,40+6=46(个)。
答:这箱苹果至少有46个。
随堂练习
1.判断下面的说法是否正确,并说一说你的理由。
(1)把0.56扩大到它的100倍是560。
(2)0是正数。
(3)假分数的倒数一定都是真分数。
(4)所有的偶数都是合数。
(5)a(a为整数,a>1)的所有因数都小于a。
【教材P74 练习十四 第6题】
×
56
×
0既不是正数,也不是负数
×
分子、分母相同的假分数的倒数依然是假分数
×
2是质数
×
a的因数还包括它本身
2.数字2、3、4、5能组成多少个没有重复数字的两位数?
(1)这些两位数中,哪些是奇数?哪些是偶数?
【教材P74 练习十四 第5题】
23,24,25,32,34,35,42,43,45,52,53,54,共12个
奇数:23,25,35,43,45,53
偶数:24,32,34,42,52,54
2.数字2、3、4、5能组成多少个没有重复数字的两位数?
(2)这些两位数中,哪些是质数?哪些是合数?
【教材P74 练习十四 第5题】
23,24,25,32,34,35,42,43,45,52,53,54,共12个
质数:23,43,53
合数:24,25,32,34,35,42,45,52,54
2.数字2、3、4、5能组成多少个没有重复数字的两位数?
(3)这些两位数中,哪些是2的倍数?哪些是3的倍数?哪些是5的倍数?
【教材P74 练习十四 第5题】
23,24,25,32,34,35,42,43,45,52,53,54,共12个
2的倍数:24,32,34,42,52,54
3的倍数:24,42,45,54
5的倍数:25,35,45
2.数字2、3、4、5能组成多少个没有重复数字的两位数?
(4)这些两位数中,2和3的公倍数有___________,3
和5的公倍数是______。
【教材P74 练习十四 第5题】
23,24,25,32,34,35,42,43,45,52,53,54,共12个
24,42,54
45
3.找规律,填数。
(1)0.9,0.99,0.999,0.9999,( ),…,这列数越来越大,越来越接近( )。
(2) , , , , ,( ),…,这列数越来越小,越来越接近( )。
【教材P74 练习十四 第7题】
0.99999
1
0
4.比较 、 、 、 的大小。你能发现什么?根据你发现的规律猜一下 与 哪个更大,并设法验证。
【教材P74 练习十四 第8题】
发现:分母与分子的差相等的真分数相比较,分母越大这个分数就越大。
猜想:
证明:
因为 ,所以 。
课堂小结
倍数
2的倍数特征
5的倍数特征
3的倍数特征
偶数
奇数
因数(非0自然数)
1
质数
合数
一、判断。(对的画“√”,错的画“×”)
20÷4=5,那么4叫因数,20叫倍数。 ( )
两个质数一定是互质数,两个合数一定不是互质数。
( )
×
×
巩固练习
三个连续自然数的和一定是6的倍数。 ( )
×
4.所有偶数(0除外)的最大公因数是2。
( )
5.两个不同数的最小公倍数一定大于最大公因数。
( )
√
√
